centos下安装配置redis7
1、找个目录下载安装包
sudo wget https://download.redis.io/release/redis-7.0.0.tar.gz

2、将tar.gz包解压至指定目录下
sudo mkdir /home/redis
sudo tar -zxvf redis-7.0.0.tar.gz -C /home/redis
3、安装gcc-c++
yum install gcc-c++
4、切换到redis-7.0.0目录下

5、修改redis.conf配置文件
注释掉ip绑定

保护模式下添加redis密码

更改端口
![]()
守护进程改为yes即可后台运行
6、设置防火墙允许端口
firewall-cmd --zone=public --add-port=6380/tcp --permanent
firewall-cmd --reload
7、启动redis-server
sudo /home/redis-7.0.0/src/redis-server redis.conf

查看进程
ps -aux | grep redis

8、使用密码进入redis
cd src
sudo ./redis-cli -p 6380
auth 密码

9、在redis连接工具rdm上测试,进行如下配置,redis7之后用户名默认为default,也可以不填
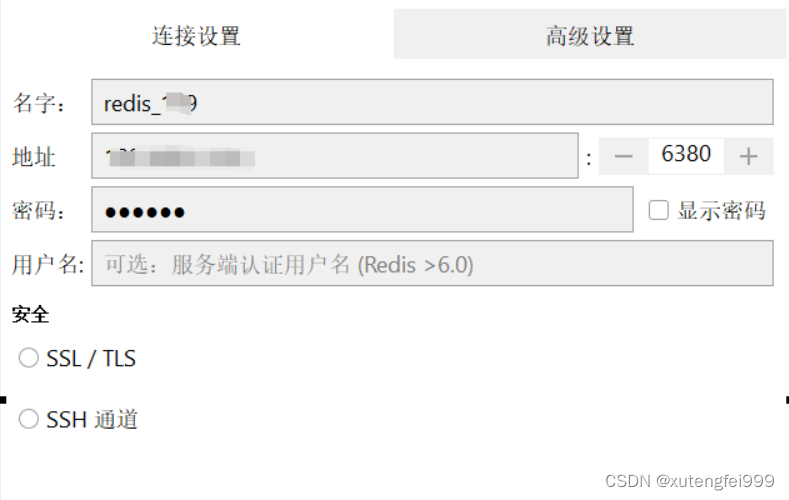
点击连接,显示连接成功
相关文章:

centos下安装配置redis7
1、找个目录下载安装包 sudo wget https://download.redis.io/release/redis-7.0.0.tar.gz 2、将tar.gz包解压至指定目录下 sudo mkdir /home/redis sudo tar -zxvf redis-7.0.0.tar.gz -C /home/redis 3、安装gcc-c yum install gcc-c 4、切换到redis-7.0.0目录下 5、修改…...
【angular】TodoList小项目(已开源)
参考:https://segmentfault.com/a/1190000013519099 文章目录 准备工作headerTodo、Doing、Done样式(HTMLCSS)功能(TS)将输入框内容加入todoList(addTodo)将todo事件改到doing 服务 参考开源 效…...

【Java 进阶篇】HTML块级元素详解
HTML(Hypertext Markup Language)是用于创建网页的标记语言。在HTML中,元素被分为块级元素和内联元素两种主要类型。块级元素通常用于构建网页的结构,而内联元素则嵌套在块级元素内,用于添加文本和其他内容。本文将重点…...

CSS设置鼠标样式和添加视频样式
鼠标的样式 <div style"cursor: default">默认鼠标的样式</div><div style"cursor: pointer">小手样式</div><div style"cursor: move">移动样式</div><div style"cursor: text">文本样式&…...
项目文件上传到行云codeup teambition
接手公司好几年的老项目,在行云上已经有1.9G的大小所以被限制上传了 只有花钱扩容或者重新建库。 1.重新建库:登录你的行云账户在代码库中新建代码库(网上有详细的) 创建成功后的库中只有readme文件。 2.复制代码库的下载地址 …...

现货黄金和实物黄金有什么区别?
在黄金投资市场中,现货黄金和实物黄金都是两种比较受欢迎的黄金投资品种。想想越来越多人认识到黄金投资的重要性,那么要选择一个投资品种,应该选哪个黄金投资品种呢?下面我们就来讨论一下这两者有何区别,以及投资者应…...
)
/dev下没有video0这个文件(ubuntu无法打开摄像头)
文章目录 硬件问题一、查看虚拟机摄像头连接情况二、解决红色报错三、虚拟机硬件处理内容问题一、设备号二、视频格式问题硬件问题 一、查看虚拟机摄像头连接情况 报错详情 ERROR: cannot launch node of type [image_view/image_view]: image_view ROS path [0]=/opt/ros/m…...

mysql面试题32:MySQL数据库服务器性能分析的方法命令有哪些?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:MySQL数据库服务器性能分析的方法命令有哪些? MySQL数据库服务器性能分析的方法和命令有以下几种: EXPLAIN命令:用于分析查询语句的执行计划,…...
伦敦银最新价格能进吗?
不少新手的伦敦银投资者由于看不懂行情走势,在行情机会来临时总感觉患得患失,但由于又十分渴望在这个市场上实现收益,所以经常通过各种各样的方式方法和手段,希望行情走势什么时候会出现进场的机会。 可以肯定的是,伦敦…...

【计算机毕设案例推荐】洋州影院购票管理系统SpringBoot+Vue
前言:我是IT源码社,从事计算机开发行业数年,专注Java领域,专业提供程序设计开发、源码分享、技术指导讲解、定制和毕业设计服务 项目名 基于SpringBoot的洋州影院购票管理系统 技术栈 SpringBootVueMySQLMaven 文章目录 一、洋州…...

Java设计模式之模板方法模式
模板方法模式(Template Method Pattern)是一种行为型设计模式,它定义了一个算法骨架,将一些步骤的具体实现延迟到子类中。模板方法模式通过将共同的代码逻辑放在父类中,而将具体的实现细节留给子类来实现,从…...
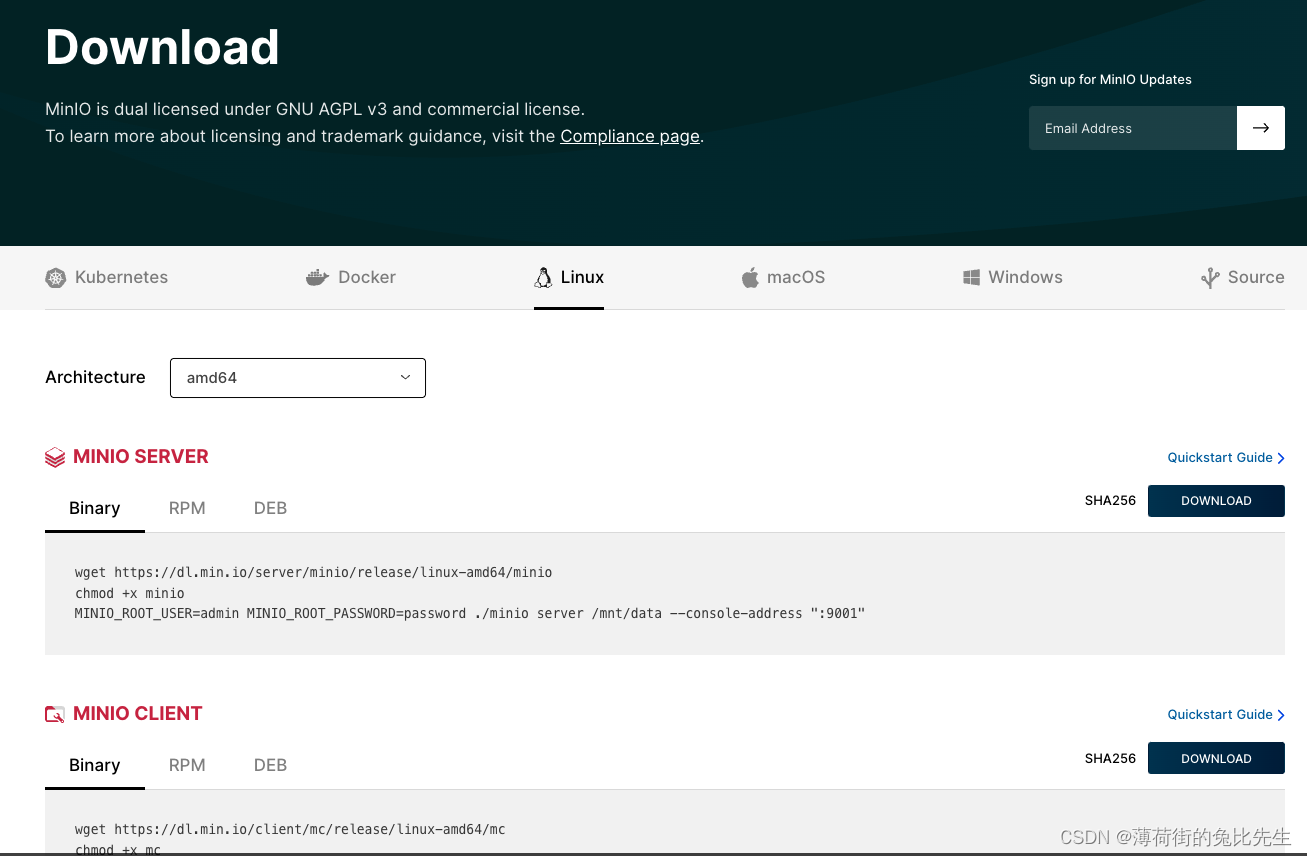
MinIO的安装与使用
文章目录 1.MINIO是什么?2.MINIO安装3.启动脚本4.打开MINIO页面5.MC命令6.MINIO备份脚本 1.MINIO是什么? MinIO 是一款高性能、分布式的对象存储系统. 它是一款软件产品, 可以100%的运行在标准硬件。即X86等低成本机器也能够很好的运行MinIO。 MinIO与…...

“==”和equals的区别
总结几句话: 双等号始终是 1.基本数据类型:比较存储的值是否相等。 2.引用数据类型:比较所指对象的地址值是否相等。 equals 1.没有被重写过: 相当于;但是不能比较基本数据类型,比较的是引用对象的所指…...

QT - 对话框去掉标题栏问号
要去掉 Qt 对话框的标题栏上的问号图标,你可以使用 Qt::CustomizeWindowHint 标志来定制对话框的窗口样式。 以下是一个示例代码,演示如何去掉标题栏上的问号图标: #include <QDialog> #include <QDialogButtonBox> #include &…...

FPGA---UDP通信求助
项目场景: 使用UDP进行回环,网络调试助手,发送数据通过UDP接收模块接收,解析出数据,给到UDP发送模块,传回上位机。 问题描述 UDP接收模块中,接收到的CRC校验值与自己计算CRC校验值进行判断&am…...
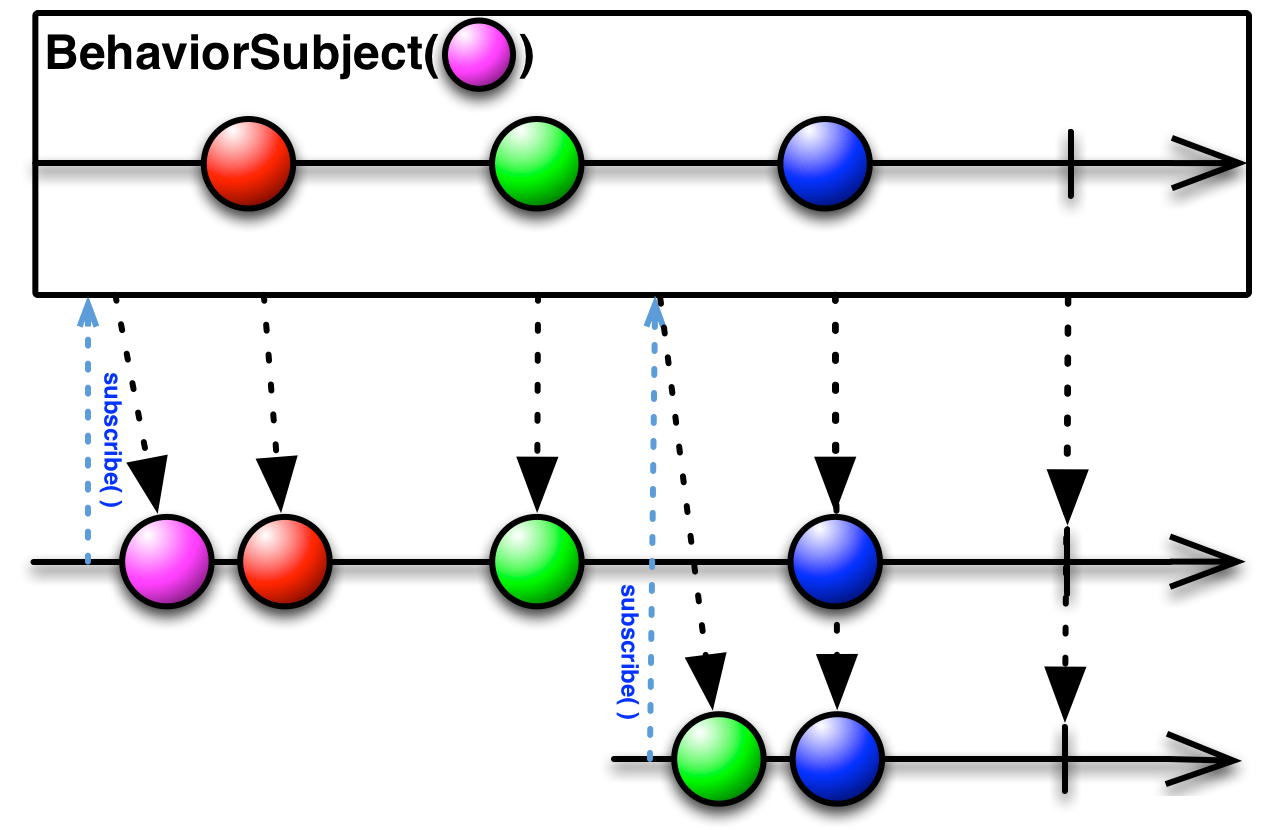
RxJava介绍及基本原理
随着互联网的迅猛发展,Java已成为最广泛应用于后端开发的语言之一。而在处理异步操作和事件驱动编程方面,传统的Java多线程并不总是最佳选择。这时候,RxJava作为一个基于观察者模式、函数式编程和响应式编程理念的库,为我们提供了…...
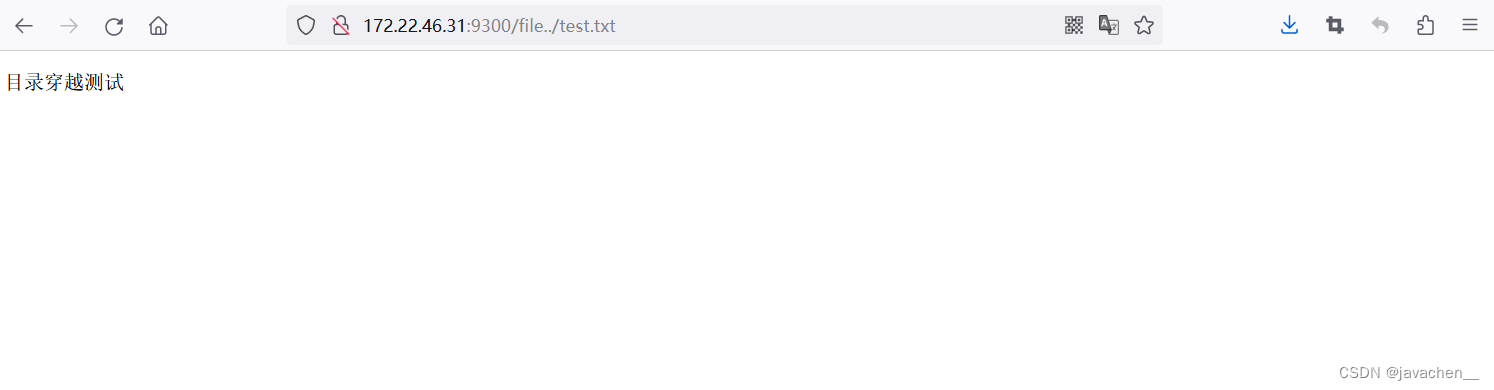
nginx目录穿越
测试nginx版本为nginx/1.23.3 location /file {alias /home/;} 在/usr跟目录下新建a.txt测试文件 通过访问 http://{ip}:{端口}/file../test.txt 实现目录穿越 防护:location与alias的值都加上/或不加/...

stl String
构造函数 表达式 效果 string s 生成一个空的 string s string s(str) Copy 构造函数,创建一个 string str 的拷贝 string s(rvStr) Move 构造函数,创建一个 string 并将 rvStr 的内容搬移给 s string s(str,stridx) 将 string str 内“始于位置…...

java通过ffmpeg将wav音频文件转广播音频编码-G.711文件发送
1.直接将wav文件转g711 [ffmpeg.exe -i F:\\tt\\2.wav -f s16le -ar 8k -ac 1 -acodec pcm_s16le F:\\tt\\2pcm.g711] String cmdFfmpeg = "ffmpeg -i "+localUrl...

【Spring】Springmvc执行流程
介绍 SpringMVC是一种基于Spring实现了Web MVC设计模式的请求驱动类型的轻量级Web框架,使用了MVC的架构模式思想,将Web层进行指责解耦,并管理应用所需的生命周期,为简化日常开发,提供了很大便利。 组件 组件Dispatche…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
