2023 NOIP A层联测9 - 风信子 题解
思路
我们可以考虑设 f l 0 , r 0 , l 1 , r 1 f_{l_0,r_0,l_1,r_1} fl0,r0,l1,r1 表示最大的 a l − a r a_l-a_r al−ar,其中 l ∈ [ l 0 , r 0 ] l\in [l_0,r_0] l∈[l0,r0], r ∈ [ l 1 , r 1 ] r\in [l_1, r_1] r∈[l1,r1]。
于是如果我们能够快速求出 f f f 值,那么我们就能解决问题。
考虑如何快速求 f f f 值。
发现似乎没有什么好方法,但是我们在某些特殊情况下是可以快速求的,即当 l 0 = l 1 l_0=l_1 l0=l1, r 0 = r 1 r_0=r_1 r0=r1 或 r 0 < l 1 r_0<l_1 r0<l1 时,我们可以用线段树快速求出其 f f f 值。
我们又发现刚开始给出的左右两边端点能取的区间是一样的,于是我们考虑当取出这区间的最大值之后,如何拆分区间使得拆分出来的区间满足上面的特殊情况。
当 l 0 = l 1 l_0=l_1 l0=l1, r 0 = r 1 r_0=r_1 r0=r1 时,我们假设此时最大值的为 a x − a y a_x - a_y ax−ay,当我们取出 a x − a y a_x - a_y ax−ay 后,我们就不能再取 ( x , y ) (x,y) (x,y) 这对数了,此时我们的左右端点的区间会改变,于是我们可以将改变后的区间拆为如下六种形式。
- 左端点 ∈ [ l , x − 1 ] \in [l, x - 1] ∈[l,x−1],右端点 ∈ [ l , x − 1 ] \in[l, x - 1] ∈[l,x−1],此时 x > l x > l x>l。
- 左端点 ∈ [ l , x − 1 ] \in [l, x - 1] ∈[l,x−1],右端点 ∈ [ x , r ] \in[x, r] ∈[x,r],此时 x > l x > l x>l。
- 左端点 ∈ [ x , x ] \in [x, x] ∈[x,x],右端点 ∈ [ x , x ] \in[x, x] ∈[x,x],此时 x ≠ y x \not = y x=y。
- 左端点 ∈ [ x , x ] \in [x, x] ∈[x,x],右端点 ∈ [ x + 1 , y − 1 ] \in[x + 1, y - 1] ∈[x+1,y−1],此时 x < y − 1 x < y - 1 x<y−1。
- 左端点 ∈ [ x , x ] \in [x, x] ∈[x,x],右端点 ∈ [ y + 1 , r ] \in[y + 1, r] ∈[y+1,r],此时 y > r y > r y>r。
- 左端点 ∈ [ x + 1 , r ] \in [x + 1,r] ∈[x+1,r],右端点 ∈ [ x + 1 , r ] \in[x + 1, r] ∈[x+1,r],此时 x < r x < r x<r。
因为此时 l 0 = l 1 l_0 = l_1 l0=l1, r 0 = r 1 r_0 = r_1 r0=r1,所以我们用 l l l, r r r 代替。
注意一下后面的条件,要满足其这个取值区间才会存在。
还有一种情况为 r 0 < l 1 r_0<l_1 r0<l1,此时拆分形式如下。
- 左端点 ∈ [ l 0 , x − 1 ] \in [l_0, x - 1] ∈[l0,x−1],右端点 ∈ [ l 1 , r 1 ] \in[l_1, r_1] ∈[l1,r1],此时 l 0 < x l_0 < x l0<x。
- 左端点 ∈ [ x , x ] \in [x, x] ∈[x,x],右端点 ∈ [ l 1 , y − 1 ] \in[l_1, y - 1] ∈[l1,y−1],此时 l 1 < y l_1 < y l1<y。
- 左端点 ∈ [ x , x ] \in [x, x] ∈[x,x],右端点 ∈ [ y + 1 , r 1 ] \in[y + 1, r_1] ∈[y+1,r1],此时 y < r 1 y < r_1 y<r1。
- 左端点 ∈ [ x + 1 , r 0 ] \in [x + 1, r_0] ∈[x+1,r0],右端点 ∈ [ l 1 , r 1 ] \in[l_1, r_1] ∈[l1,r1],此时 x < r 0 x < r_0 x<r0。
于是我们发现,当我们满足特殊条件时的区间,取出最大值后还是能变成满足特殊条件的区间,于是我们就可以做出来了。
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL inf = 1e16;
int n, Q, a[100005];
LL bz[5000005];
struct Grid {LL val; int id;friend bool operator> (Grid a, Grid b) { return a.val > b.val; }friend bool operator< (Grid a, Grid b) { return a.val < b.val; }
} maxn[5000005], minn[5000005];
struct Ans {LL val; int x, y;friend bool operator> (Ans a, Ans b) { return a.val > b.val; }friend bool operator< (Ans a, Ans b) { return a.val < b.val; }
} ans[5000005];
inline void updata(int x) {maxn[x] = max(maxn[x * 2], maxn[x * 2 + 1]);minn[x] = min(minn[x * 2], minn[x * 2 + 1]);ans[x] = max(ans[x * 2], ans[x * 2 + 1]);if (maxn[x * 2].val - minn[x * 2 + 1].val > ans[x].val)ans[x].val = maxn[x * 2].val - minn[x * 2 + 1].val, ans[x].x = maxn[x * 2].id, ans[x].y = minn[x * 2 + 1].id;
}
inline void build(int x, int l, int r) {if (l == r) {maxn[x].val = minn[x].val = a[l], ans[x].val = 0;maxn[x].id = minn[x].id = ans[x].x = ans[x].y = l;return ;}int mid = l + r >> 1;build(x * 2, l, mid), build(x * 2 + 1, mid + 1, r);updata(x);
}
inline void pushdown(int x) {maxn[x].val += bz[x], minn[x].val += bz[x];bz[x * 2] += bz[x], bz[x * 2 + 1] += bz[x];bz[x] = 0;
}
inline void add(int x, int l, int r, int sl, int sr, int val) {pushdown(x);if (r < sl || sr < l)return ;if (sl <= l && r <= sr) {bz[x] += val;pushdown(x);return ;}int mid = l + r >> 1;add(x * 2, l, mid, sl, sr, val), add(x * 2 + 1, mid + 1, r, sl, sr, val);updata(x);
}
inline Grid find_max(int x, int l, int r, int sl, int sr) {pushdown(x);if (r < sl || sr < l)return { -inf, 0 };if (sl <= l && r <= sr)return maxn[x];int mid = l + r >> 1;return max(find_max(x * 2, l, mid, sl, sr), find_max(x * 2 + 1, mid + 1, r, sl, sr));
}
inline Grid find_min(int x, int l, int r, int sl, int sr) {pushdown(x);if (r < sl || sr < l)return { inf, 0 };if (sl <= l && r <= sr)return minn[x];int mid = l + r >> 1;return min(find_min(x * 2, l, mid, sl, sr), find_min(x * 2 + 1, mid + 1, r, sl, sr));
}
inline Ans find_ans(int x, int l, int r, int sl, int sr) {pushdown(x);if (r < sl || sr < l)return { -inf, 0, 0 };if (sl <= l && r <= sr)return ans[x];int mid = l + r >> 1;Ans t = max(find_ans(x * 2, l, mid, sl, sr), find_ans(x * 2 + 1, mid + 1, r, sl, sr));Grid a = find_max(x * 2, l, mid, sl, sr), b = find_min(x * 2 + 1, mid + 1, r, sl, sr);t = max(t, {a.val - b.val, a.id, b.id});return t;
}
struct node {int il, ir, jl, jr;LL val;Ans Val() {if (ir < jl) {Grid l = find_max(1, 1, n, il, ir), r = find_min(1, 1, n, jl, jr);return { l.val - r.val, l.id, r.id };}elsereturn find_ans(1, 1, n, il, ir);}friend bool operator< (node a, node b) { return a.val < b.val; }
} ;
priority_queue <node> q;
int main() {scanf("%d%d", &n, &Q);for (int i = 1; i <= n; i++)scanf("%d", &a[i]);build(1, 1, n);while (Q--) {int opt, L, R, k;scanf("%d%d%d%d", &opt, &L, &R, &k);if (opt == 1)add(1, 1, n, L, R, k);else {node t;t.il = t.jl = L, t.jr = t.ir = R;t.val = t.Val().val;q.push(t);LL sum = 0;while (k) {node now = q.top();Ans val = now.Val();int x = val.x, y = val.y;q.pop(), k--;sum = sum + val.val;if (now.ir < now.jl) {if (x > now.il) {t.il = now.il, t.ir = x - 1, t.jl = now.jl, t.jr = now.jr;t.val = t.Val().val;q.push(t);}if (now.jl < y) {t.il = x, t.ir = x, t.jl = now.jl, t.jr = y - 1;t.val = t.Val().val;q.push(t);}if (y < now.jr) {t.il = x, t.ir = x, t.jl = y + 1, t.jr = now.jr;t.val = t.Val().val;q.push(t);}if (x < now.ir) {t.il = x + 1, t.ir = now.ir, t.jl = now.jl, t.jr = now.jr;t.val = t.Val().val;q.push(t);}}else {int l = now.il, r = now.ir;if (x > l) {t.il = l, t.ir = x - 1, t.jl = l, t.jr = x - 1;t.val = t.Val().val;q.push(t);t.il = l, t.ir = x - 1, t.jl = x, t.jr = r;t.val = t.Val().val;q.push(t);}if (x != y) {t.il = x, t.ir = x, t.jl = x, t.jr = x;t.val = t.Val().val;q.push(t);}if (x < y - 1) {t.il = x, t.ir = x, t.jl = x + 1, t.jr = y - 1;t.val = t.Val().val;q.push(t);}if (y < r) {t.il = x, t.ir = x, t.jl = y + 1, t.jr = r;t.val = t.Val().val;q.push(t);}if (x < r) {t.il = x + 1, t.ir = r, t.jl = x + 1, t.jr = r;t.val = t.Val().val;q.push(t);}}}printf("%lld\n", sum);while (!q.empty())q.pop();}}return 0;
}
相关文章:

2023 NOIP A层联测9 - 风信子 题解
思路 我们可以考虑设 f l 0 , r 0 , l 1 , r 1 f_{l_0,r_0,l_1,r_1} fl0,r0,l1,r1 表示最大的 a l − a r a_l-a_r al−ar,其中 l ∈ [ l 0 , r 0 ] l\in [l_0,r_0] l∈[l0,r0], r ∈ [ l 1 , r 1 ] r\in [l_1, r_1] r∈[l1,r1…...

岩土工程安全监测无线振弦采集仪在无线组网的关键要点
岩土工程安全监测无线振弦采集仪在无线组网的关键要点 岩土工程是一种奇特而又极其重要的工程。它涉及到土地、岩石、气候等等因素,需要重视安全因素。而无线振弦采集仪作为一种常用的监测设备,可以采集岩土工程中的振动数据,从而确保工程的…...

代码随想录Day14 LeetCodeT110平衡二叉树 T257二叉树的所有路径 T404 左叶子之和
以下思路来自于: 代码随想录 (programmercarl.com) LeetCode T110 平衡二叉树 题目链接:110. 平衡二叉树 - 力扣(LeetCode) 题目思路 前面我们说过了,求二叉树的深度我们应该使用前序遍历,求二叉树的高度我们应该使用后序遍历,因为后序遍历可以将子树的…...
C语言自定义类型_枚举联合(3)
目录 枚举 什么是枚举类型? 枚举的声明 枚举的定义 枚举的优点 枚举的使用 联合(共用体) 什么是联合呢? 联合类型的定义 联合的特点 联合使用 联合大小的计算 联合的应用 今天接着我们来结束自定义类型。Ἑ…...
asp.net网上销售系统VS开发mysql数据库web结构c#编程Microsoft Visual Studio计算机毕业设计
一、源码特点 asp.net 网上销售系统 是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为mysql,使用c#语言开发 aspnet 网上销售系统1 二、功能介绍 前台功能…...
【Windows】RPC调用过程实例详解
概述:windows 创建 RPC调用过程实例详解 参考文章:Remote procedure call (RPC)(远程过程调用 (RPC)) - Win32 apps | Microsoft Learn 文章目录 0x01、生成 UUID 和模版(IDL)文件0x02、添加 acf 文件0x03、编译 idl 文件0x04、客…...
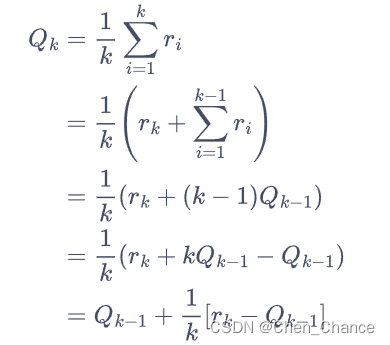
动手学强化学习第2章多臂老虎机
2.1简介 多臂老虎机问题可以被看作简化版的强化学习问题。但是其只有动作和奖励没有状态信息,算是简化版的强化学习问题。 2.2问题介绍 2.2.1问题定义 在多臂老虎机(MAB)问题中,有一个有K根拉杆的老虎机,拉动每一根拉杆都对应一个关于奖励…...

钡铼BL124EC实现EtherCAT转Ethernet/IP的优势
钡铼技术的BL124EC是一款用于将EtherCAT从站转换为Ethernet/IP从站的网关设备。它是钡铼技术开发的高性能、可靠的工业自动化通信解决方案之一。 添加图片注释,不超过 140 字(可选) BL124EC网关可以应用于多种工业自动化场景,以下…...

使用IntelliJ Idea必备的插件!
趁手的工具让开发事半功倍,好用的IDEA插件让效率加倍。 今天给大家分享几个优秀的IDEA插件。 插件安装 首先得知道在IDEA哪安装插件? 点击File---->Settings---->找到Plugins标签,即可搜索想要的插件进行安装了。 现在来看下有哪些值…...

代码随想录算法训练营第23期day19| 654.最大二叉树、617.合并二叉树、700.二叉搜索树中的搜索、98.验证二叉搜索树
目录 一、(leetcode 654)最大二叉树 二、(leetcode 617)合并二叉树 三、(leetcode 700)二叉搜索树中的搜索 四、(leetcode 98)验证二叉搜索树 一、(leetcode 654&…...
 459. 重复的子字符串)
第四章 字符串part02 28. 实现strStr() 459. 重复的子字符串
第四章 字符串part02 28. 实现strStr() 459. 重复的子字符串 一、28. 实现strStr() 题目链接:https://leetcode.cn/problems/repeated-substring-pattern/ 题目介绍: 给定一个非空的字符串 s ,检查是否可以通过由它的一个子串重复多次构成。…...
设计模式 - 状态模式
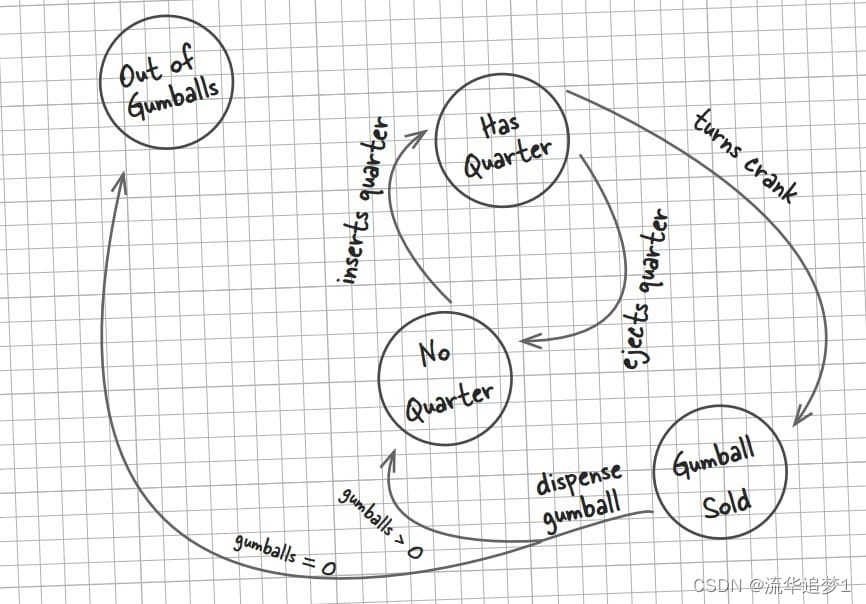
目录 一. 前言 二. 实现 一. 前言 状态模式(State Pattern):它主要用来解决对象在多种状态转换时,需要对外输出不同的行为的问题。状态和行为是一一对应的,状态之间可以相互转换。当一个对象的内在状态改变时&#x…...

【vim 学习系列文章 9 -- .vim 脚本文件开发学习】
文章目录 .vimrc 介绍.vim 脚本文件开发 .vimrc 介绍 在Vim中,你可以将一系列的Vim命令和设置写入一个脚本文件中,并使用:source命令来运行它。这种脚本文件通常被称为vimrc文件,因为它的默认名称是.vimrc。通常,我们将这个文件放…...

NAT模式和桥接模式的区别
NAT模式和桥接模式的区别 NAT模式和桥接模式都是虚拟机网络配置的两种方式,主要区别在于虚拟机与外部网络交互的方式不同。 NAT(Network Address Translation,网络地址转换)模式:在这种模式下,虚拟机和宿主…...

应对出海安全合规挑战,兆珑科技为什么选择了亚马逊云科技?
在中国企业出海进程中,安全合规是企业面临的首要挑战。尤其是当企业业务涉及金融相关领域时,面临着最为严苛的安全合规要求。 深圳兆珑科技有限公司是一家全球化的物联网生态企业,其业务覆盖100多个国家和地区,在欧洲、南美、亚太…...
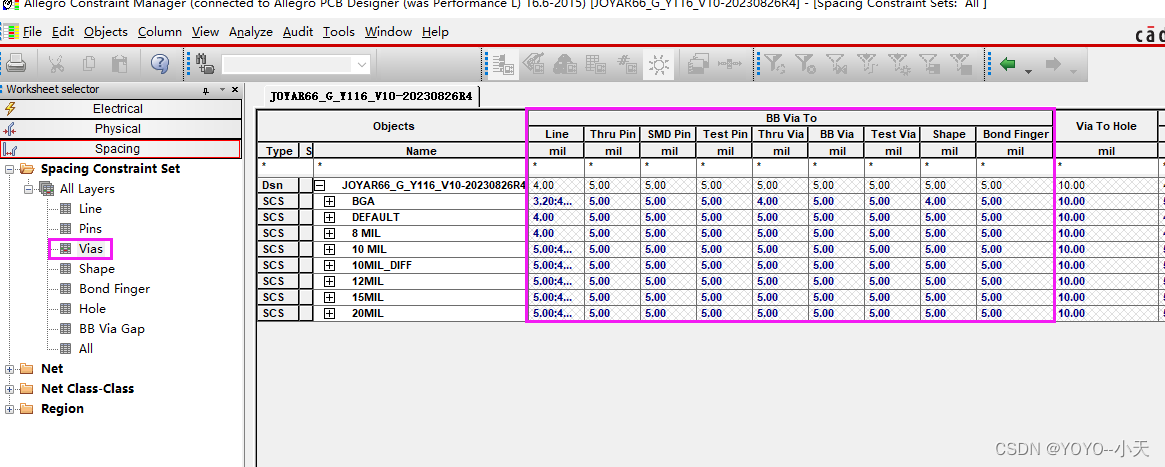
Allegro基本规则设置指导书之Spacing规则设置
进入规则设置界面 1.设置Line 到其他的之间规则: 2.设置Pins 到其他的之间规则: 3.设置Vias 到其他的之间规则:...
使用【Blob、Base64】两种方式显示【文本、图片、视频】 使用 video 组件播放视频
Blob 显示 Blob 对象的类型是由 MIME 类型(Multipurpose Internet Mail Extensions)来确定的。MIME 类型是一种标准,用于表示文档、图像、音频、视频等多媒体文件的类型。以下是一些常见的 Blob 对象类型: text/plain࿱…...

深度学习_1_基本语法
数据结构 代码: import torchx torch.arange(12)##产生长度为12的一维张量print(x)##X x.resize(3, 4)##被弃用##print(X)y torch.reshape(x, (3, 4))##修改向量为矩阵,一维变二维print(y)print(y.size())xx torch.zeros((2, 3, 4))##三维矩阵&…...
c#设计模式-行为型模式 之 中介者模式
🚀简介 又叫调停模式,定义一个中介角色来封装一系列对象之间的交互,使原有对象之间的耦合松散,且可以独立地改变它们之间的交互。 从下右图中可以看到,任何一个类的变 动,只会影响的类本身,以及…...
小程序uView2.X框架upload组件上传方法总结+避坑
呈现效果: 1.1单图片上传 1.2多图片上传 前言:相信很多人写小程序会用到uView框架,总体感觉还算OK吧,只能这么说,肯定也会遇到图片视频上传,如果用到这个upload组件相信你,肯定遇到各种各样的问题,这是我个人总结的单图片和多图片上传方法. uView2.X框架:uView 2.0 - 全面兼容…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
