一文讲解图像梯度
简介:
图像梯度计算的是图像变化的幅度。对于图像的边缘部分,其灰度值变化较大,梯度值变化也较大;相反,对于图像中比较平滑的部分,其灰度值变化较小,相应的梯度值变化也较小。一般情况下,图像梯度计算的是图像的边缘信息。它在图像处理和计算机视觉中具有重要的应用,常用于边缘检测、特征提取和图像增强等任务。
图像梯度概念:
图像梯度就是对图像的X轴,Y轴求其变化率,是一个二维的向量,分别表示X轴的变化和Y轴的变化:
其中:
- X轴的变化是指当前像素右侧(X加1)的像素值减去当前像素左侧(X减1)的像素值。
- Y轴的变化是当前像素下方(Y加1)的像素值减去当前像素上方(Y减1)的像素值。
将计算出来的两个分量合并在一起,形成一个二维向量就得到了图像梯度。
推导:
首先我们先来看一下数学知识微积分的求导的过程:
这里是对图像的一阶微分,但是图像时一个二维的向量,假设我们设该函数为f(x,y),我们看一下微积分中对两个未知数的微分,这里就是求偏导的内容
对x方向的求导:
对y方向的求导:
这里求导,高数的知识说这个值应该趋近于0,这样才能求的偏导,也就是
无限小,但是对于图像来说
取不到很小的值,图像中的像素离散的,最小的距离应为1。因此这里我们令
等于1。那么上面的公式就变为:
这样我们就得到了图像的梯度公式,仔细观察我们可以看到图像梯度可以近似为相邻像素的差值。
上述两个公式对所有 和
的有关值可用下图的一维模板对
的滤波得到。

用于计算梯度偏导数的滤波器模板,通常称之为梯度算子、边缘算子和边缘检测子等。
对于不同的滤波器模板得到的梯度是不同的,这也就衍生出很多算子,如Roberts、Prewitt、Sobel和Laplacian算子等。下面将详细介绍不同的算子。
梯度算子
梯度简单来说就是求导。OpenCV 提供了三种不同的梯度滤波器,或者说高通滤波器:Sobel Scharr 和Laplacian 。什么叫高通呢?其实就是和图像模糊相反。图像模糊是让低频通过,阻挡高频,这样就可以去除噪点,让锐利的边缘变平滑。高通滤波器就是让高频通过,阻挡低频,可以让边缘更加明显,增强图像。
Roberts 算子:
Roberts算子即交叉微分算子,是基于交叉差分的梯度算子。此算法通过局部差分来计算检测图像的边缘线条,对噪声敏感。
Roberts交叉微分算子分别为主对角线和副对角线方向的算子,有两个2*2的滤波算子组成:

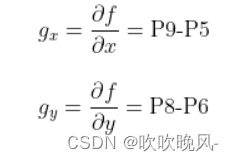
Prewitt 算子:
Prewitt算子是一种图像边缘检测的微分算子,其原理是利用特定区域内像素灰度值产生的差分实现边缘检测。由于Prewitt算子采用 33 模板对区域内的像素值进行计算,而Robert算子的模板为 22,故Prewitt算子的边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。Prewitt算子适合用来识别噪声较多、灰度渐变的图像,其计算公式如下所示:
例如,下面给出Prewitt算子的模板,在像素点P5处 和
方向上的梯度大小分别计算为:


Prewitt算子的边缘检测结果在水平方向和垂直方向均比Robert算子更加明显。
Sobel算子:
Sobel算子,主要用作边缘检测,是离散差分算子,用来运算图像梯度函数的灰度近似值。Sobel算子具有一定的平滑作用,对噪声不敏感。在图像的任何一点使用此算子,将会产生对应的梯度矢量或者法矢量。其中Sobel算子x轴y轴卷积核如下:

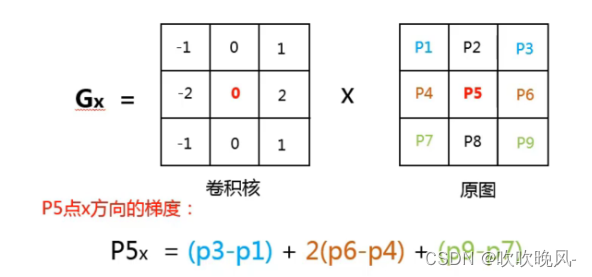

如上图我们可以看到对P5这个点求x轴,y轴的梯度。以Gx为例,P5的x轴梯度公式是:
P5 = (P3-P1)+2(P6-P4)+(P9-P7)
这里我们可以看到,由于P6和P4距离P5较近,对P5的影响较大,所以给予了一个较大的权重2,从差值中我们可以看到,P5右边的值减去P5左边的值,假设两边差值较大说明P5这个点位于边界,两边差值较小,说明P5在图像变化较为平缓区域。
下面我们使用python代码对其实现:
# coding:utf-8
import cv2
import numpy as np# Scharr算子实现梯度计算
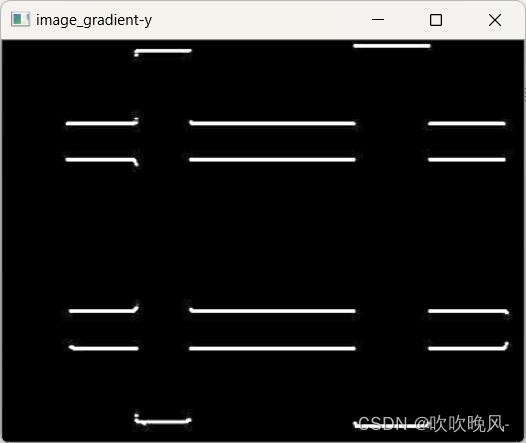
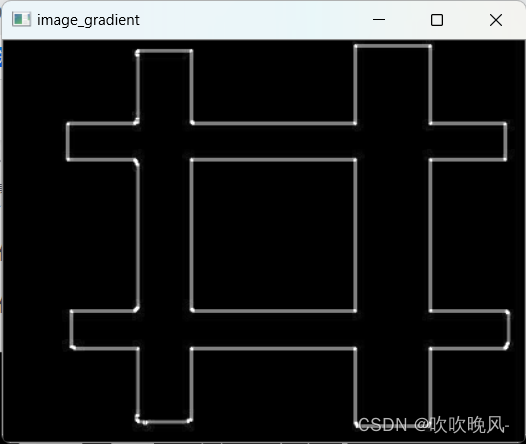
def Scharr_demo(image):# x 方向梯度image_grad_x = cv2.Sobel(image, cv2.CV_32F, 1, 0)# y 方向梯度image_grad_y = cv2.Sobel(image, cv2.CV_32F, 0, 1)# 分别求绝对值并转化为8位的图像上,这样做方便显示image_gradx = cv2.convertScaleAbs(image_grad_x)image_grady = cv2.convertScaleAbs(image_grad_y)# 显示两个方向图像cv2.imshow("image_gradient-x", image_gradx)cv2.imshow("image_gradient-y", image_grady)# 两个方向梯度的叠加,权重各自一半image_gradxy = cv2.addWeighted(image_gradx, 0.5, image_grady, 0.5, 0)cv2.imshow("image_gradient", image_gradxy)if __name__ == '__main__':image = cv2.imread("a.jpg")cv2.imshow("src_image", image)Scharr_demo(image)cv2.waitKey(0)cv2.destroyAllWindows()这里我们使用第一张图进行求图像梯度结果图如下:


Scharr算子:
在离散的空间上,有很多方法可以用来计算近似导数,在使用3×3的Sobel算子时,可能计算结果并不太精准。下面我们介绍Scharr算子,该算子具有和Sobel算子同样的速度,且精度更高。可以将Scharr算子看作对Sobel算子的改进,其核通常为:
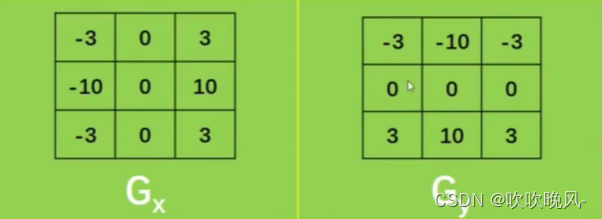
梯度的计算方法与Sobel算子一样,下面我们使用Python对其进行实现:
#coding:utf-8
import cv2
import numpy as np# Scharr算子实现梯度计算
def Scharr_demo(image):# x 方向梯度image_grad_x = cv2.Scharr(image, cv2.CV_32F, 1, 0)# y 方向梯度image_grad_y = cv2.Scharr(image, cv2.CV_32F, 0, 1)# 分别求绝对值并转化为8位的图像上,这样做方便显示image_gradx = cv2.convertScaleAbs(image_grad_x) image_grady = cv2.convertScaleAbs(image_grad_y)# 显示两个方向图像cv2.imshow("image_gradient-x", image_gradx)cv2.imshow("image_gradient-y", image_grady)#两个方向梯度的叠加,权重各自一半image_gradxy = cv2.addWeighted(image_gradx, 0.5, image_grady, 0.5, 0)cv2.imshow("image_gradient", image_gradxy)if __name__ == '__main__':image = cv2.imread("./test01.jpg")cv2.imshow("src_image", image)Scharr_demo(image)cv2.waitKey(0)cv2.destroyAllWindows()这里我们依旧使用第一张图进行求图像梯度结果图如下:



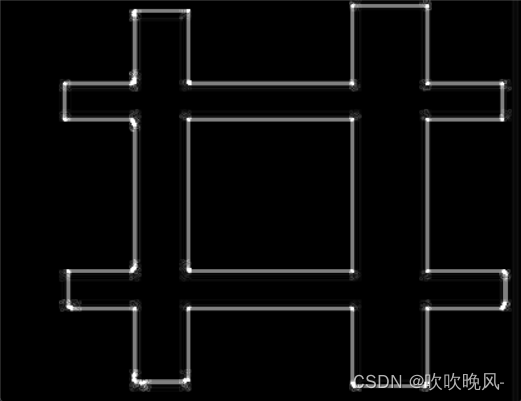
Sobel算子与Scharr算子比较:
Sobel算子的缺点是,当其核结构较小时,精确度不高,而Scharr算子具有更高的精度。
下面我们对两个算子对图像处理的结果进行展示:



这里第一张为原始图像,第二张是通过Sobel求图像梯度,第三张是通过Scharr算子求图像梯度。
Laplacian 算子:
Laplacian(拉普拉斯)算子是一种二阶导数算子,其具有旋转不变性,可以满足不同方向的图像边缘锐化(边缘检测)的要求。通常情况下,其算子的系数之和需要为零。例如,一个
3×3 大小的 Laplacian 算子如图 所示。

Laplacian 算子类似二阶 Sobel 导数,需要计算两个方向的梯度值。
为了更适合于数字图像处理,将该方程表示为离散形式:
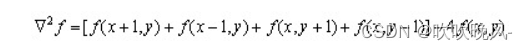
另外,拉普拉斯算子还可以表示成模板的形式,以便更好编程需要。如下图所示。
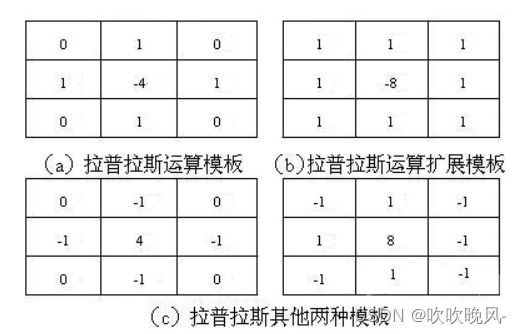
图(a)表示离散拉普拉斯算子的模板,图(b)表示其扩展模板,图(c)则分别表示其他两种拉普拉斯的实现模板。从模板形式容易看出,如果在图像中一个较暗的区域中出现了一个亮点,那么用拉普拉斯运算就会使这个亮点变得更亮。因为图像中的边缘就是那些灰度发生跳变的区域,所以拉普拉斯锐化模板在边缘检测中很有用。一般增强技术对于陡峭的边缘和缓慢变化的边缘很难确定其边缘线的位置。但此算子却可用二次微分正峰和负峰之间的过零点来确定,对孤立点或端点更为敏感,因此特别适用于以突出图像中的孤立点、孤立线或线端点为目的的场合。同梯度算子一样,拉普拉斯算子也会增强图像中的噪声,有时用拉普拉斯算子进行边缘检测时,可将图像先进行平滑处理。
图像锐化处理的作用是使灰度反差增强,从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算,因此可以对图像进行逆运算,如微分运算能够突出图像细节,使图像变得更为清晰。由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加而产生锐化图像。拉普拉斯锐化的基本方法可以由下式表示:

这种简单的锐化方法既可以产生拉普拉斯锐化处理的效果,同时又能保留背景信息,将原始图像叠加到拉普拉斯变换的处理结果中去,可以使图像中的各灰度值得到保留,使灰度突变处的对比度得到增强,最终结果是在保留图像背景的前提下,突现出图像中小的细节信息。但其缺点是对图像中的某些边缘产生双重响应。
各类算子的优缺点:
(1)Roberts 算子
Roberts算子利用局部差分算子寻找边缘,边缘定位精度较高,但容易丢失一部分边缘,不具备抑制噪声的能力。该算子对具有陡峭边缘且含噪声少的图像效果较好,尤其是边缘正负45度较多的图像,但定位准确率较差;
(2) Prewitt 算子
Prewitt算子对灰度渐变的图像边缘提取效果较好,而没有考虑相邻点的距离远近对当前像素点的影响,与Sobel 算子类似,不同的是在平滑部分的权重大小有些差异;
(3)Sobel 算子
Sobel算子考虑了综合因素,对噪声较多的图像处理效果更好,Sobel 算子边缘定位效果不错,但检测出的边缘容易出现多像素宽度。
(4)Scharr算子
Scharr算子,该算子具有和Sobel算子同样的速度,且精度更高。可以将Scharr算子看作对Sobel算子的改进。
(5)Laplacian 算子
Laplacian 算子不依赖于边缘方向的二阶微分算子,对图像中的阶跃型边缘点定位准确,该算子对噪声非常敏感,它使噪声成分得到加强,这两个特性使得该算子容易丢失一部分边缘的方向信息,造成一些不连续的检测边缘,同时抗噪声能力比较差,由于其算法可能会出现双像素边界,常用来判断边缘像素位于图像的明区或暗区,很少用于边缘检测。
相关文章:

一文讲解图像梯度
简介: 图像梯度计算的是图像变化的幅度。对于图像的边缘部分,其灰度值变化较大,梯度值变化也较大;相反,对于图像中比较平滑的部分,其灰度值变化较小,相应的梯度值变化也较小。一般情…...

湖州OLED透明拼接屏技术应用引领现代化旅游观光方式
湖州市位于中国浙江省北部,拥有悠久的历史和丰富的文化遗产。湖州市以其美丽的湖泊和秀丽的自然风光而闻名。 作为中国重要的历史文化名城之一,湖州市有着丰富的文化遗产和历史资源,如古城墙、古建筑和古镇等。 这为OLED透明拼接屏技术的应用…...
)
点云从入门到精通技术详解100篇-点云特征学习模型及其在配准中的应用(续)
目录 基于局部邻域的点云特征学习模型 3.1引言 3.2自适应邻域选择算法...

铁道交通运输运营3D模拟仿真实操提供一个沉浸、高效且环保的情境
VR模拟果蔬运输应急处理场景在农产品物流行业中具有重要的意义。这种模拟技术为农产品运输提供了全新的、更高效和更安全的方式来模拟真实世界的应急情况,帮助操作人员、研究者和管理者更好地理解和应对可能的运输风险措施。 VR模拟果蔬运输应急处理场景可以模拟出各…...

yum apt pip 阿里云源
centos yum 阿里云源 # 备份 mv /etc/yum.repos.d/CentOS-Base.repo /etc/yum.repos.d/CentOS-Base.repo.backup# centos 6 wget -O /etc/yum.repos.d/CentOS-Base.repo https://mirrors.aliyun.com/repo/Centos-vault-6.10.repo curl -o /etc/yum.repos.d/CentOS-Base.repo h…...

Python+Tkinter 图形化界面基础篇:多线程和异步编程
PythonTkinter 图形化界面基础篇:多线程和异步编程 引言为什么需要多线程和异步编程?使用多线程多线程示例步骤 1 :导入必要的模块步骤 2 :创建主窗口和按钮步骤 3 :创建下载线程步骤 4 :启动主事件循环 使…...
)
第13章 并发编程高阶(二)
13.11 Reentrantlock和Synchronized有哪些区别 难度:★★ 重点:★★ 白话解析 继续串线,搞明白了锁的设计,那Java设计的Reentrantlock锁和JVM底层的synchronized锁到底有什么区别呢。 参考答案 1、底层实现层面 synchronized 是JVM层面的锁,是Java关键字 reentrantlock…...
)
Android AMS——栈管理详解(十一)
上一篇我们找到了栈管理所在的方法,这里继续对内部方法进行详细分析。 setInitialState:初始化函数。 computeLaunchingTaskFlags:检查 Activity 的启动模式。 computeSourceRootTask:处理源 Activity 的所在栈。 getReusableTask:获取能够复用的 Task。 computeTargetTas…...
【Redis】Set集合相关的命令
目录 命令SADDSMEMBERSSISMEMBERSCARDSPOPSMOVESREMSINTERSINTERSTORESUNIONSUNIONSTORESDIFFSDIFFSTORE 命令 SADD 将⼀个或者多个元素添加到set中。注意,重复的元素⽆法添加到set中。 SADD key member [member ...]SMEMBERS 获取⼀个set中的所有元素࿰…...
力扣第501题 二叉树的众数 c++ (暴力 加 双指针优化)
题目 501. 二叉搜索树中的众数 简单 相关标签 树 深度优先搜索 二叉搜索树 二叉树 给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。 …...

MARKDOWN 文档图片编码嵌入方案
#1 写在前面 开始写这篇文章时,标题怎么定困扰我良久,缘于不晓得如何给接下来要做的事定个简单明了的标题:在📱终端只能纯文本交互的前提下,优雅展示 markdown 文档中的图片。这也许比问题本身还要棘手😄。…...

KubeVela可持续测试应用部署之Mock基础设施
Mock接口是我们常用的功能测试方案,有时候依赖的接口未开发完成或者依赖的第三方接口不提供测试环境等,只有Mock才能跑通流程。 我们基于KubeVela开发的云原生应用交付平台,提供如初始化基础设施导入、中间件部署共用基础设施等相关能力的测试,需要依赖基础设施。虽然terr…...

代理IP、Socks5代理与网络工程:解析技术世界的无限可能
在当今数字化的世界中,网络工程师不仅需要保证网络的稳定性,还要应对多样的技术挑战。代理IP和Socks5代理技术已经成为网络工程师工具箱中不可或缺的利器,在跨界电商、爬虫、出海、网络安全、游戏等领域发挥关键作用。本文将深入探讨这两项技…...

OpenCV级联分类器识别车辆实践笔记
1. OpenCV 级联分类器的基本原理 基于Haar特征的级联分类器的目标检测是Paul Viola和Michael Jones在2001年的论文中提出的一种有效的目标检测方法。这是一种基于机器学习的方法,从大量的正面和负面图像中训练级联函数。然后用它来检测其他图像中的物体。 Haar特征…...
VS编译的时候不生成Release文件夹
方法描述: Build>Configuration Manager>Release 编译》配置管理》选择发布版本 再编译就有了 具体操作过程 第一步: 第二步: 第三步: 特此记录 anlog 2023年10月12日...
14.2 Socket 反向远程命令行
在本节,我们将继续深入探讨套接字通信技术,并介绍一种常见的用法,实现反向远程命令执行功能。对于安全从业者而言,经常需要在远程主机上执行命令并获取执行结果。本节将介绍如何利用 _popen() 函数来启动命令行进程,并…...
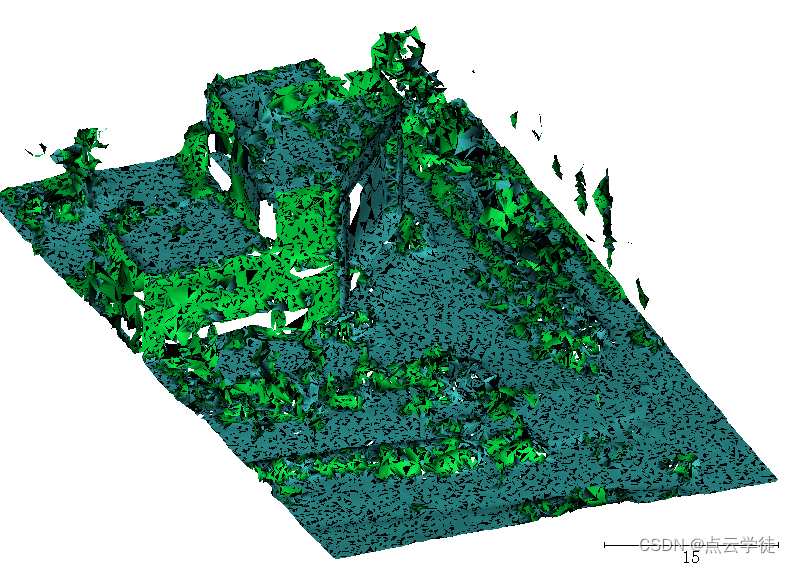
PCL点云处理之点云重建为Mesh模型并保存到PLY文件 ---方法二 (二百一十一)
PCL点云处理之点云重建为Mesh模型并保存到PLY文件 ---方法二 (二百一十一) 一、算法介绍二、算法实现1.代码2.效果一、算法介绍 离散点云重建为mesh网格模型,并保存到PLY文件中,用于其他软件打开查看,代码非常简短,复制粘贴即可迅速上手使用,具体参数根据自己的点云数据…...
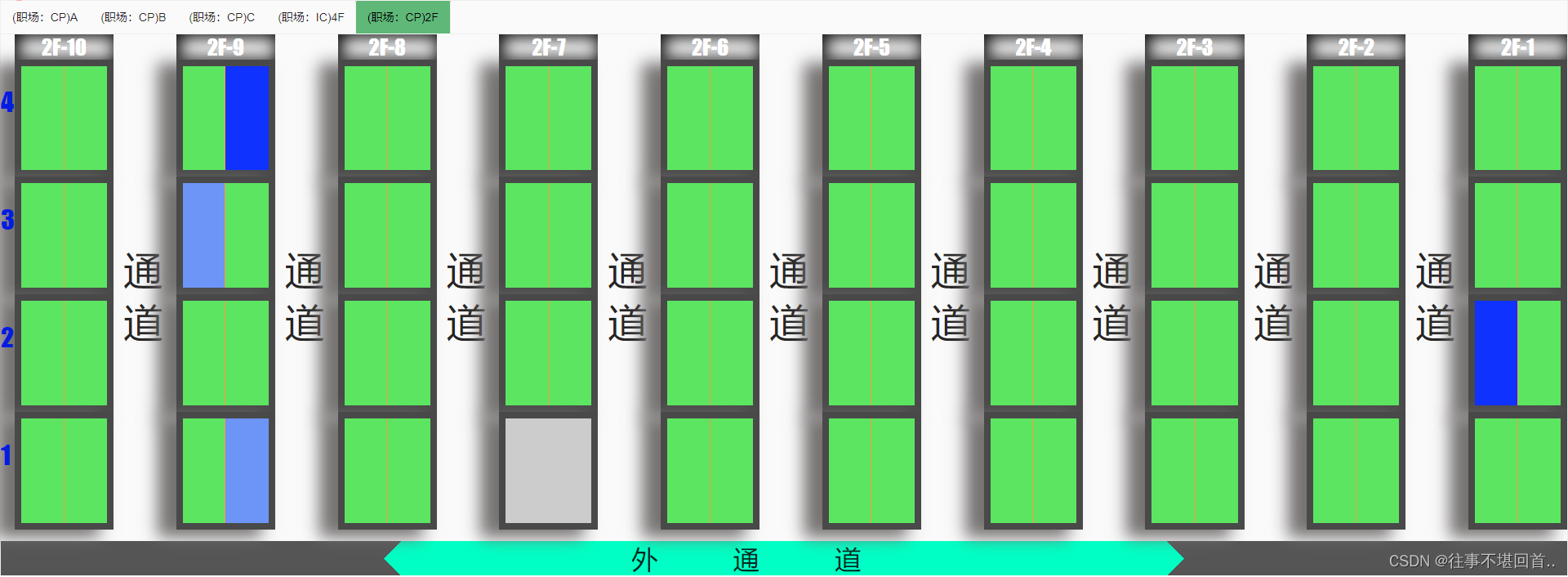
CSS 中::after的妙用(实现在margin中显示内容)
效果图如下: 背景: 如上图,之前只是当纯的写一个参考货架平面图,用作物料系统的在库状态可视化,当完成页面body分成10等份时,货架之间需要有通道,为了实现实际的样式,我给每个等份都…...

SentenceTransformer使用多GPU加速向量化
文章目录 前言代码 前言 当我们需要对大规模的数据向量化以存到向量数据库中时,且服务器上有多个GPU可以支配,我们希望同时利用所有的GPU来并行这一过程,加速向量化。 代码 就几行代码,不废话了 from sentence_transformers i…...

架构师-软件工程习题选择题
架构师-软件工程习题选择题 真题案例题 真题 c 瀑布模型:针对软件需求明确的情况,将前一个阶段做完,才能开始下一个阶段 原型模型:针对需求不明确的情况,快速搭建出系统原型,然后根据系统原型和客户确认需求…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...
