用3-8译码器实现全减器
描述
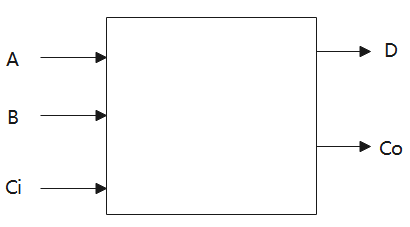
请使用3-8译码器和必要的逻辑门实现全减器,全减器接口图如下,A是被减数,B是减数,Ci是来自低位的借位,D是差,Co是向高位的借位。
3-8译码器代码如下,可将参考代码添加并例化到本题答案中。
module decoder_38(input E ,input A0 ,input A1 ,input A2 ,output reg Y0n , output reg Y1n , output reg Y2n , output reg Y3n , output reg Y4n , output reg Y5n , output reg Y6n , output reg Y7n
);always @(*)beginif(!E)beginY0n = 1'b1;Y1n = 1'b1;Y2n = 1'b1;Y3n = 1'b1;Y4n = 1'b1;Y5n = 1'b1;Y6n = 1'b1;Y7n = 1'b1;end else begincase({A2,A1,A0})3'b000 : beginY0n = 1'b0; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b001 : beginY0n = 1'b1; Y1n = 1'b0; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b010 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b0; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b011 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b0; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b100 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b0; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b101 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b0; Y6n = 1'b1; Y7n = 1'b1;end 3'b110 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b0; Y7n = 1'b1;end 3'b111 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b0;end default: beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;endendcase end
end endmodule
输入描述
input A ,input B ,input Ci 输出描述
output wire D ,output wire Co 解题分析
3-8译码器实现全减器
38译码器的输出实际上包含了输入A2 A1 A0组成的所有最小项,而全减器作为组合电路,其输出最终可化简为最小项的形式。
由于译码器的输出为最小项取反,而逻辑函数可以写成最小项之和的形式,故可以利用门电路和译码器实现逻辑函数。
需先列出全减器的真值表。
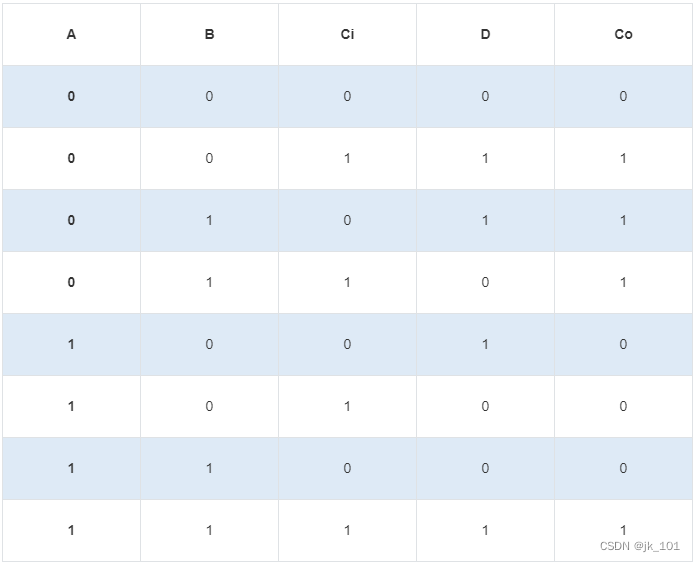
由真值表可得出,输出D的逻辑表达式用最小项表示为:
D = m1+m2+m4+m7输出Co的逻辑表达式用最小项表示为:
Co = m1+m2++m3+m7由于译码器的输出为最小项取反,下面需要将表达式中的最小项转换为最小项取反的形式。根据反演定理,转换结果如下:
D = (m1’m2’m4’m7’)’;Co=(m1’m2’m3’m7’)’‘表示取反。
由上式可知,采用与非门即可实现该电路的组合逻辑输出。关键电路如下:
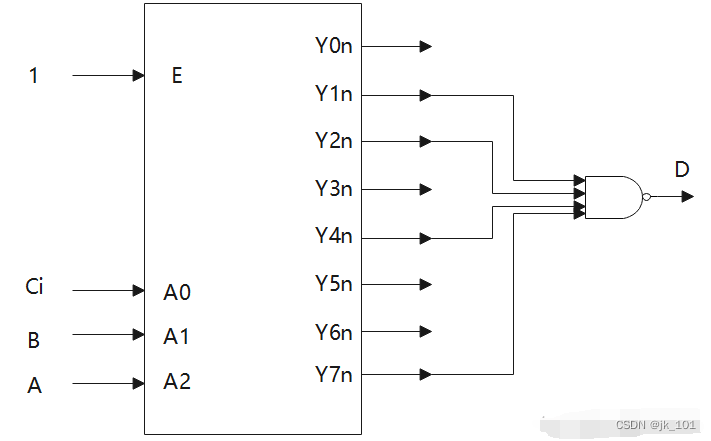
上图中D和Co的输入端来自同一各译码器。
结合电路图,将电路转换成Verilog代码描述如下:
wire Y0_n ; wire Y1_n ;wire Y2_n ;wire Y3_n ;wire Y4_n ;wire Y5_n ;wire Y6_n ;wire Y7_n ;decoder_38 U0(.E (1'b1),.A0 (Ci ),.A1 (B ),.A2 (A ),.Y0n (Y0_n), .Y1n (Y1_n),.Y2n (Y2_n),.Y3n (Y3_n),.Y4n (Y4_n),.Y5n (Y5_n),.Y6n (Y6_n),.Y7n (Y7_n));assign D = ~(Y1_n & Y2_n & Y4_n & Y7_n);assign Co = ~(Y1_n & Y2_n & Y3_n & Y7_n);参考代码
`timescale 1ns/1nsmodule decoder_38(input E ,input A0 ,input A1 ,input A2 ,output reg Y0n , output reg Y1n , output reg Y2n , output reg Y3n , output reg Y4n , output reg Y5n , output reg Y6n , output reg Y7n
);always @(*)beginif(!E)beginY0n = 1'b1;Y1n = 1'b1;Y2n = 1'b1;Y3n = 1'b1;Y4n = 1'b1;Y5n = 1'b1;Y6n = 1'b1;Y7n = 1'b1;end else begincase({A2,A1,A0})3'b000 : beginY0n = 1'b0; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b001 : beginY0n = 1'b1; Y1n = 1'b0; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b010 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b0; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b011 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b0; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b100 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b0; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;end 3'b101 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b0; Y6n = 1'b1; Y7n = 1'b1;end 3'b110 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b0; Y7n = 1'b1;end 3'b111 : beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b0; Y7n = 1'b0;end default: beginY0n = 1'b1; Y1n = 1'b1; Y2n = 1'b1; Y3n = 1'b1; Y4n = 1'b1; Y5n = 1'b1; Y6n = 1'b1; Y7n = 1'b1;endendcase end
end endmodulemodule decoder1(input A ,input B ,input Ci ,output wire D ,output wire Co
);wire Y0_n ;
wire Y1_n ;
wire Y2_n ;
wire Y3_n ;
wire Y4_n ;
wire Y5_n ;
wire Y6_n ;
wire Y7_n ;decoder_38 U0(.E (1'b1),.A0 (Ci ),.A1 (B ),.A2 (A ),.Y0n (Y0_n), .Y1n (Y1_n), .Y2n (Y2_n), .Y3n (Y3_n), .Y4n (Y4_n), .Y5n (Y5_n), .Y6n (Y6_n), .Y7n (Y7_n)
);assign D = ~(Y1_n & Y2_n & Y4_n & Y7_n);
assign Co = ~(Y1_n & Y2_n & Y3_n & Y7_n);endmodule注:解题分析来源于网友,如有侵权,请告删之。
相关文章:

用3-8译码器实现全减器
描述 请使用3-8译码器和必要的逻辑门实现全减器,全减器接口图如下,A是被减数,B是减数,Ci是来自低位的借位,D是差,Co是向高位的借位。 3-8译码器代码如下,可将参考代码添加并例化到本题答案中。 …...
招投标系统简介 企业电子招投标采购系统源码之电子招投标系统 —降低企业采购成本
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...
Linux Centos7 下使用yum安装的nginx平滑升级
1. 查看当前nginx版本 1nginx -v2. 查看centos版本 1cat /etc/redhat-release3. 创建一个新的文件nginx.repo,其中第三行的7是因为我的centos版本是7点多的,你看自己是多少就改多少 1vim /etc/yum.repos.d/nginx.repo23[nginx]4namenginx repo 5baseu…...

C/S架构学习之多线程实现TCP并发服务器
并发概念:并发是指两个或多个事件在同一时间间隔发生;多线程实现TCP并发服务器的实现流程:一、创建套接字(socket函数):通信域选择IPV4网络协议、套接字类型选择流式; int sockfd socket(AF_IN…...
iPhone手机记笔记工具选择用哪个
iPhone手机大家应该都比较熟悉,其使用性能是比较流畅的,在iPhone手机上记录笔记可以帮助大家快速地进行总结工作、记录工作内容等,在iPhone手机上记笔记工具选择用哪个呢? 可以在iPhone手机上使用的笔记工具是比较多的࿰…...
标签)
MyBatis动态SQL(if、choose、when和otherwise)标签
动态 SQL 是 MyBatis 的强大特性之一。在 JDBC 或其它类似的框架中,开发人员通常需要手动拼接 SQL 语句。根据不同的条件拼接 SQL 语句是一件极其痛苦的工作。例如,拼接时要确保添加了必要的空格,还要注意去掉列表最后一个列名的逗号。而动态…...
idea将jar包deploy到本地仓库
1、pom.xml文件引入配置,如下参考: <distributionManagement><snapshotRepository><id>maven-snapshots</id><url>http://nexus1.coralglobal.cn/repository/maven-snapshots/</url></snapshotRepository><…...

麻省理工学院与Meta AI共同开发StreamingLLM框架,实现语言模型无限处理长度
🦉 AI新闻 🚀 麻省理工学院与Meta AI共同开发StreamingLLM框架,实现语言模型无限处理长度 摘要:麻省理工学院与Meta AI的研究人员联合研发了一款名为StreamingLLM的框架,解决了大语言模型在RAM与泛化问题上的挑战&am…...

记录 K8S 挂了的解决经过
背景:早上到公司,有同事反馈部署K8S在集群上的 Redis 和 禅道 都不可用 排查循序: 登录 kubesphere 的 web 界面 (界面打开失败)ssh 登录主服务器 (正常)在主服务器上运行 kubectl get node 命…...

Flink---11、状态管理(按键分区状态(值状态、列表状态、Map状态、归约状态、聚合状态)算子状态(列表状态、广播状态))
星光下的赶路人star的个人主页 这世上唯一扛得住岁月摧残的就是才华 文章目录 1、状态管理1.1 Flink中的状态1.1.1 概述1.1.2 状态的分类 1.2 按键分区状态(Keyed State)1.2.1 值状态(ValueState)1.2.2 列表状态(ListS…...
Vue3中使用tinymce全功能演示,包括开源功能
效果图: 1、下载插件: npm i tinymce npm i tinymce/tinymce-vue 2、在node_modules文件夹中找到tinymce下的skins复制到项目public文件夹中 (可以先创建一个tinymce文件夹): 3、在tinymce官网中下载中文包,并放在刚…...
There was an error committing your changes: File could not be edited
使用github完成commit changes时报的一个错误,最终原因是没有填写Extended description...

10月9日,每日信息差
今天是2023年10月9日,以下是为您准备的14条信息差 第一、首只与规模挂钩型浮动费率基金即将面市。作为公募基金费率改革大背景下的首批浮动费率产品,华夏信兴回报混合是市场上首只管理费与管理规模挂钩的基金 第二、江北新区成立百亿产业发展母基金&am…...

【软考设计师】S01 数据结构 E01 线性结构 P01 线性表
线性表 前言——线性结构线性表线性表的定义线性表的特点线性表的存储结构顺序存储链式存储单链表双向链表循环链表静态链表 前言——线性结构 线性结构是一种基本的数据结构,主要用于对客观世界中具有单一前驱和后继的数据关系进行描述。线性结构的特点是数据元素…...

nginx配置https 访问
nginx 解压目录有configure文件 [rootoracledb10 ~]# which nginx1、检查nginx是否包含http_ssl_module 模块 如果出现 --with-http_ssl_module 就是已经安装了[rootoracledb10 sbin]# pwd /usr/local/nginx/sbin [rootoracledb10 sbin]# nginx -V nginx version: nginx/1.23…...

希亦CG声波清洗机:眼镜党福利,家庭必备清洗机
对于眼镜党来说最大的烦恼就是每天的佩戴和清洗,清洗是至关重要的,错误的清洗很容易引起镜片损坏,个人一直使用眼镜布清洗,除了费时费力之外清洁度也无法保证。希亦CG声波清洗机正是为了解决这一难题应运而生,可以彻底…...

2023年10月12日历史上的今天大事件早读
公元前539年10月12日波斯国王大流士的军队攻克巴比伦 1492年10月12日西班牙独立日 1492年10月12日哥伦布“发现新大陆” 1773年10月12日法国天文学家梅西叶首次发现具有螺旋结构的星系 1885年10月12日清政府改台湾府为行省 命刘铭传为台湾巡抚 1929年10月12日苏军向张学良…...
uCOSIII实时操作系统 五 任务API(时间片轮转API调度)
时间片轮转调度 时间片轮转法:主要用于分时系统中的进程调度。为了实现轮转调度,系统把所有就绪进程按照先入先出的原则排成一个队列的队首进程,让CPU上运行一个时间片的时间。时间片是一个小小的时间单位,通常为5~10ms数量级。当进程用完分…...

微信小程序项目如何用Hbuild启动,先让对方在微信开发平台将你的微信号添加成开发成员。
微信小程序项目如何用Hbuild启动,先让对方在微信开发平台将你的微信号添加成开发成员。然后在Hbuild官网下载,下载好后运行,点击文件导入项目,然后点击运行,模拟微信小程序,选择微信开发工具的地址…...
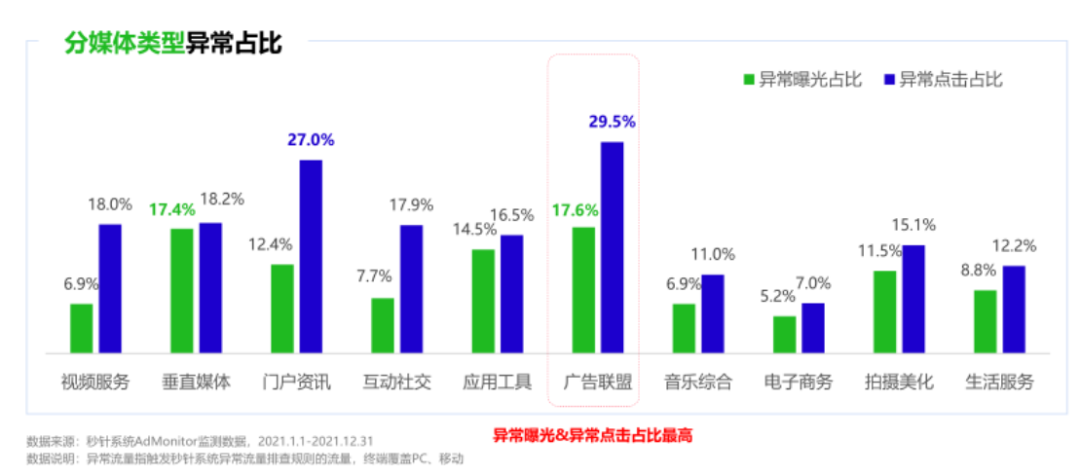
应对广告虚假流量,app广告变现该如何风控?
移动广告市场中的虚假流量一直是困扰各移动应用厂商的难题,广告作为app商业化变现最为直接快捷的途径,也引申出了流量作弊与反作弊的纷争。 根据《2021中国异常流量报告》,2021年中国品牌广告市场因异常流量造成的损失约为326亿人民币&#…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Selenium 查找页面元素的方式
Selenium 查找页面元素的方式 Selenium 提供了多种方法来查找网页中的元素,以下是主要的定位方式: 基本定位方式 通过ID定位 driver.find_element(By.ID, "element_id")通过Name定位 driver.find_element(By.NAME, "element_name"…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...

标注工具核心架构分析——主窗口的图像显示
🏗️ 标注工具核心架构分析 📋 系统概述 主要有两个核心类,采用经典的 Scene-View 架构模式: 🎯 核心类结构 1. AnnotationScene (QGraphicsScene子类) 主要负责标注场景的管理和交互 🔧 关键函数&…...

以太网PHY布局布线指南
1. 简介 对于以太网布局布线遵循以下准则很重要,因为这将有助于减少信号发射,最大程度地减少噪声,确保器件作用,最大程度地减少泄漏并提高信号质量。 2. PHY设计准则 2.1 DRC错误检查 首先检查DRC规则是否设置正确,然…...
