Layui合计自定义列
需求:第四列通过计算:27除以220

正常的汇总,增加这个属性就行

特殊的列,需要特殊处理
获取合计行:$(".layui-table-total div.layui-table-cell");
获取某列的值:$($(".layui-table-total div.layui-table-cell")[index]).html();done: function () {// 得出第四列的值 12.27%$($(".layui-table-total div.layui-table-cell")[4]).html(Utils.roundFixed(getFootValue(3) / getFootValue(2), 4) * 100 + "%")
}// 获取第几列的值
function getFootValue(index) {return Utils.parseFloat($($(".layui-table-total div.layui-table-cell")[index]).html());
}// 金额转化
Utils.parseFloat = function (num) {if (typeof num == 'string') {num = num.replace(/,/g, "");}if (!num || isNaN(num)) return 0;return parseFloat(num);
};Utils.roundFixed = function (num, fixed) {num = Utils.parseFloat(num);return Math.round(num * Math.pow(10, fixed)) / Math.pow(10, fixed);
};
相关文章:

Layui合计自定义列
需求:第四列通过计算:27除以220 正常的汇总,增加这个属性就行 特殊的列,需要特殊处理 获取合计行:$(".layui-table-total div.layui-table-cell"); 获取某列的值:$($(".layui-table-total …...
Tomcat自启动另一种方法
Tomcat自启动另一种方法 问题: 不知道怎么回事,好几台电脑都可以开机自启动tomcat,正常运行项目。一样的配置一样的操作流程,偏偏要运行的机器开机自启动后,项目不能运行,手动重启tomcat又可以用了。网上…...
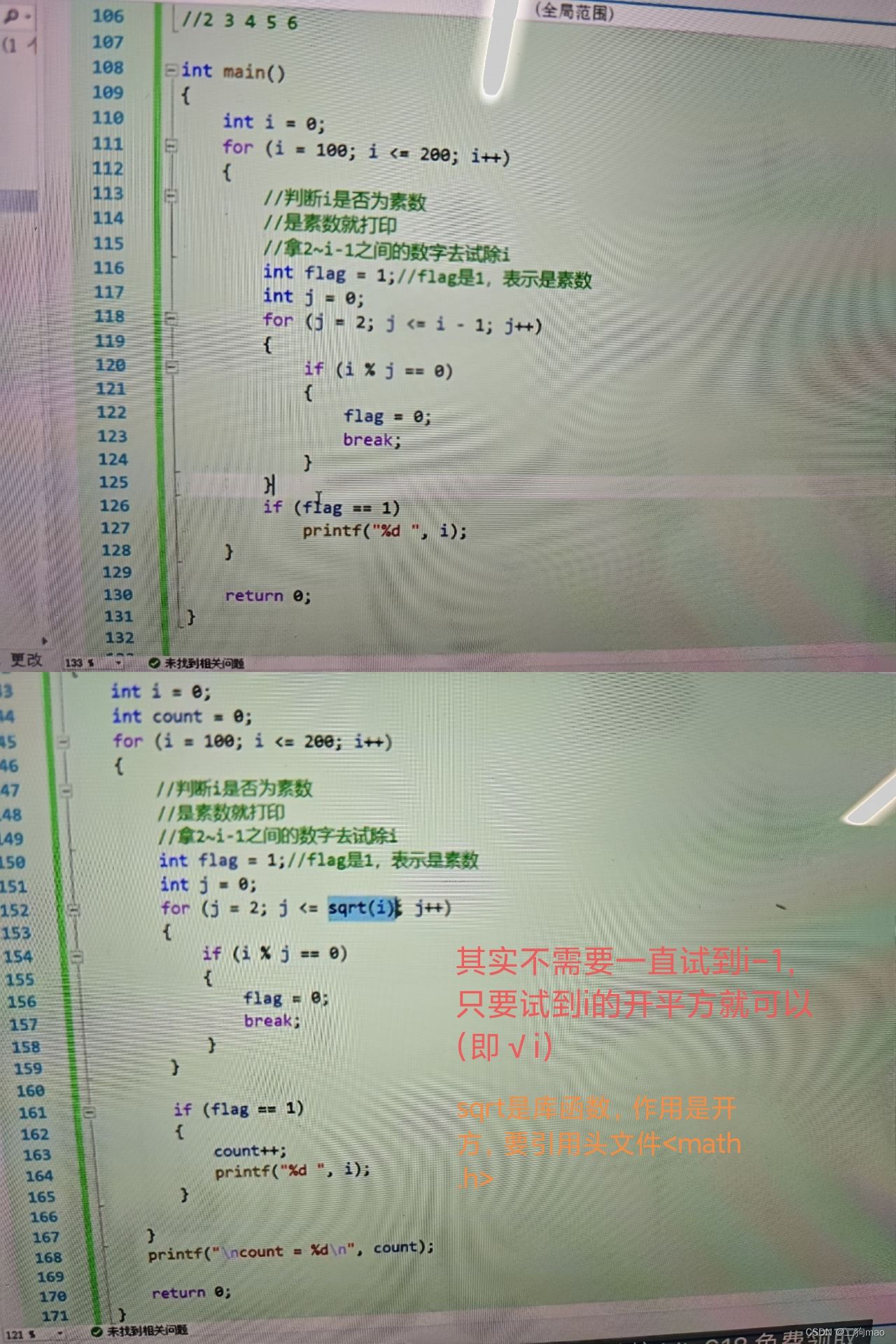
C语言,标志法
标志法通常用来检查或者进行过程中一些状态变化。 有一些是为了观察变化,举出一些以往代码的例子: 1.找出一串数字中没有重复出现过的数字 #include <stdio.h> int main() {int arr[1000] { 0 };int n 0;scanf("%d", &n);int i…...

适合自学的网络安全基础技能“蓝宝书”:《CTF那些事儿》
CTF比赛是快速提升网络安全实战技能的重要途径,已成为各个行业选拔网络安全人才的通用方法。但是,本书作者在从事CTF培训的过程中,发现存在几个突出的问题: 1)线下CTF比赛培训中存在严重的 “最后一公里”问题 &#…...

软件设计师学习笔记12-数据库的基本概念+数据库的设计过程+概念设计+逻辑设计
1.数据库的基本概念 1.1数据库的体系结构 1.1.1常见数据库 ①集中式数据库 数据是集中的;数据管理是集中的 ②C/S结构 客户端负责数据表服务;服务器负责数据库服务;系统分前后端;ODBC、JDBC ③分布式数据库 物理上分布、逻…...
distcc分布式编译
distcc https://gitee.com/bison-fork/distcc.git 下载工具链 mingw,https://www.mingw-w64.org/downloads/#w64devkitperl,https://strawberryperl.com/releases.html免安装zip版本,autoconf等脚本依赖perlautoconf、automake,…...

Java面试题-0919
集合篇 Java面试题-集合篇HashMap底层实现原理概述javaSE进阶-哈希表 为了满足hashmap集合的不重复存储,为什么要重写hashcode和equals方法? 首先理解一下hashmap的插入元素的前提: hashmap会根据元素的hashcode取模进行比较,当…...

WPF列表性能提高技术
WPF列表性能提高技术 WPF数据绑定系统不仅需要绑定功能,还需要能够处理大量数据而不会降低显示速度和消耗大量内存,WPF提供了相关的控件以提高性能,所有继承自ItemsControl的控件都支持该技术。 虚拟化 UI虚拟化是列表仅仅为当前显示项创建…...
 从初级到高级的综合指南(2))
掌握 BERT:自然语言处理 (NLP) 从初级到高级的综合指南(2)
BERT的先进技术 当您精通 BERT 后,就该探索先进技术以最大限度地发挥其潜力。在本章中,我们将深入研究微调、处理词汇外单词、领域适应,甚至从 BERT 中提取知识的策略。 微调策略:掌握适应 微调 BERT 需要仔细考虑。您不仅可以微调…...
【算法优选】 二分查找专题——贰
文章目录 😎前言🌲[山脉数组的峰顶索引](https://leetcode.cn/problems/peak-index-in-a-mountain-array/)🚩题目描述:🚩算法思路🚩代码实现: 🌴[寻找峰值](https://leetcode.cn/pro…...

SQL 的优化
SQL 优化是指对数据库查询语句进行优化,以提高查询性能和效率。下面列出了一些常见的 SQL 优化技巧: 1、索引优化 (1)使用适当的索引来加速查询操作。在频繁用于查询的列上创建索引,特别是在 WHERE 条件、JOIN 条件和…...

华为云云耀云服务器L实例评测|华为云上的CentOS性能监测与调优指南
目录 引言 编辑1 性能调优的基本要素 2 性能监控功能 2.1 监控数据指标 2.2 数据历史记录 2.3 多种统计指标 3 性能优化策略 3.1 资源分配 3.2 磁盘性能优化 3.3 网络性能优化 3.4 操作系统参数和内核优化 结论 引言 在云计算时代,性能优化和调优对于…...

Go If流程控制与快乐路径原则
Go if流程控制与快乐路径原则 文章目录 Go if流程控制与快乐路径原则一、流程控制基本介绍二、if 语句2.1 if 语句介绍2.2 单分支结构的 if 语句形式2.3 Go 的 if 语句的特点2.3.1 分支代码块左大括号与if同行2.3.2 条件表达式不需要括号 三、操作符3.1 逻辑操作符3.2 操作符的…...

yolov8 strongSORT多目标跟踪工具箱BOXMOT
1 引言 多目标跟踪MOT项目在Github中比较完整有:BOXMOT , 由mikel brostrom提供。在以前的版本中,有yolov5deepsort(版本v3-v5), yolov8strongsort(版本v6-v9),直至演变…...

如何开发一款跑酷游戏?
跑酷游戏(Parkour Game)是一种流行的视频游戏类型,玩家需要在游戏中控制角色进行极限动作、跳跃、爬墙和各种动作,以完成各种挑战和任务。如果你有兴趣开发一款跑酷游戏,以下是一些关键步骤和考虑事项: 游…...
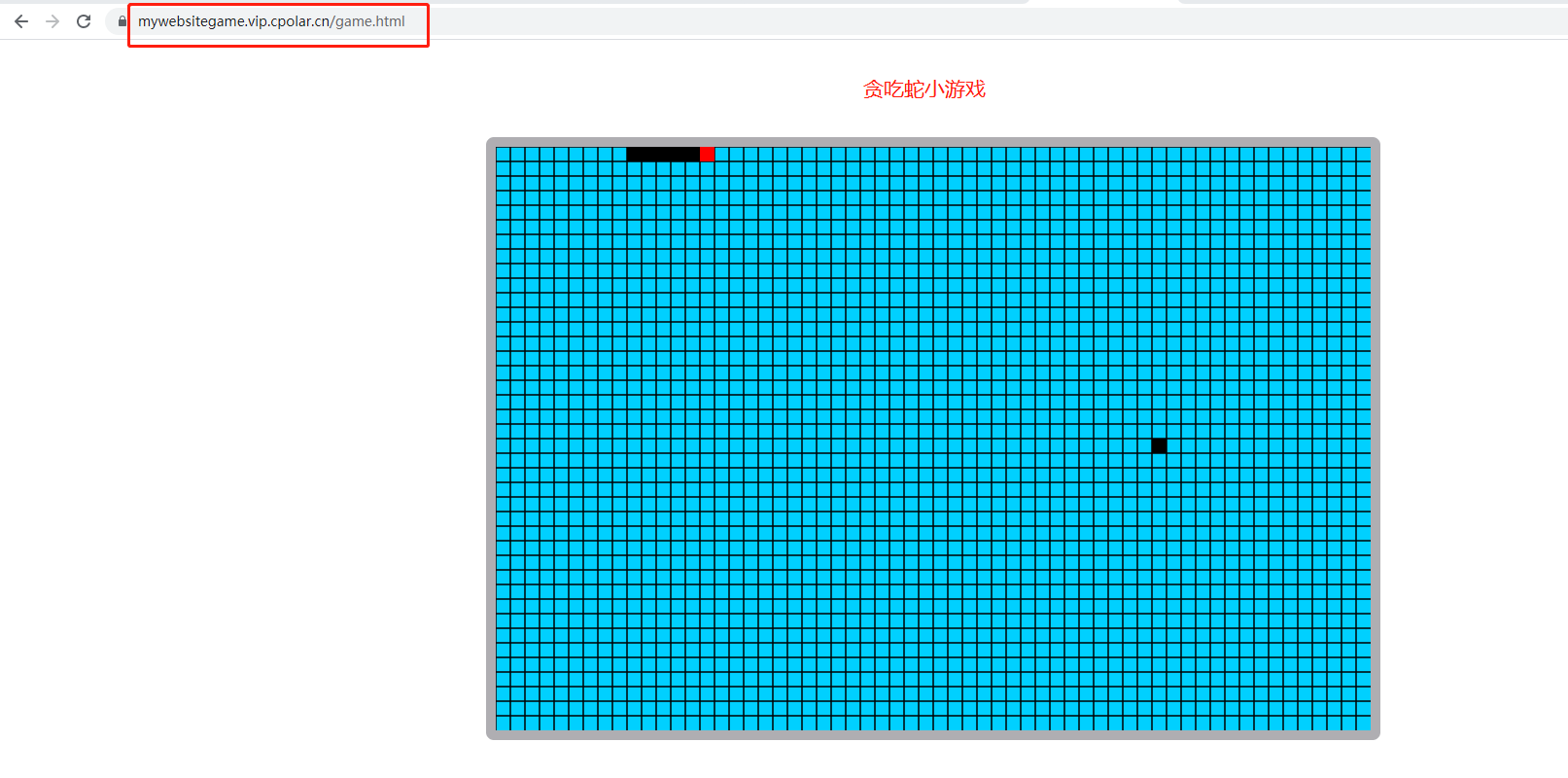
使用宝塔面板在Linux上搭建网站,并通过内网穿透实现公网访问
文章目录 前言1. 环境安装2. 安装cpolar内网穿透3. 内网穿透4. 固定http地址5. 配置二级子域名6. 创建一个测试页面 前言 宝塔面板作为简单好用的服务器运维管理面板,它支持Linux/Windows系统,我们可用它来一键配置LAMP/LNMP环境、网站、数据库、FTP等&…...

Unity可视化Shader工具ASE介绍——6、通过例子说明ASE节点的连接方式
大家好,我是阿赵。继续介绍Unity可视化Shader编辑插件ASE的用法。上一篇已经介绍了很多ASE常用的节点。这一篇通过几个小例子,来看看这些节点是怎样连接使用的。 这篇的内容可能会比较长,最终是做了一个遮挡X光的效果,不过把这…...
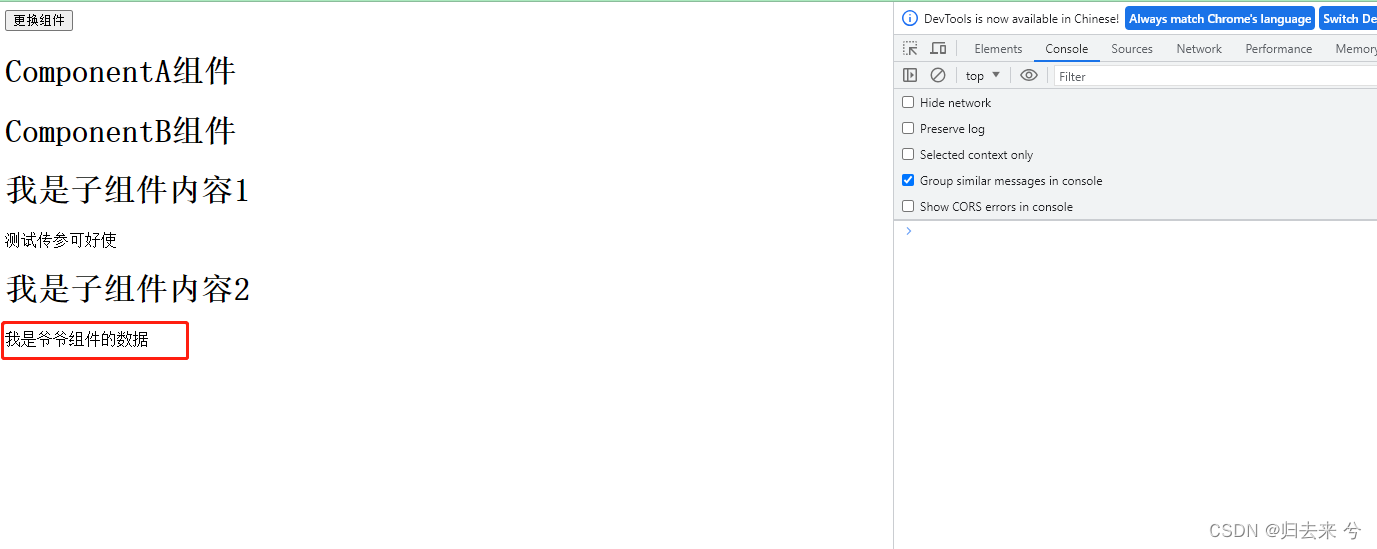
VUE3基础知识梳理
VUE3基础知识梳理 一、vue了解和环境搭建1.vue是什么:cn.vuejs.org/vuejs.org2.渐进式框架3.vue的版本4.vueAPI的风格5.准备环境5.1.创建vue项目5.2.vue的目录结构 二、vue3语法1.干净的vue项目2.模板语法2.1 文本插值2.2属性绑定2.3条件渲染2.4列表渲染2.5通过key管…...

Java架构师缓存通用设计方案
目录 1 采用多级缓存2 缓存数据尽量前移3 静态化4 数据平衡策略5 jvm缓存的问题6 redis存放数据解决7 redis垂直拆分8 总结1 采用多级缓存 在实际应用中需要考虑的实际问题。首先,前端页面可以做缓存,虽然图上没有显示,但在现实应用中这是提高性能的一个重要方面。前端页面缓…...
2023年【危险化学品生产单位安全生产管理人员】及危险化学品生产单位安全生产管理人员模拟考试题
题库来源:安全生产模拟考试一点通公众号小程序 危险化学品生产单位安全生产管理人员考前必练!安全生产模拟考试一点通每个月更新危险化学品生产单位安全生产管理人员模拟考试题题目及答案!多做几遍,其实通过危险化学品生产单位安…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
