【面试经典150 | 哈希表】存在重复元素 II
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:哈希表
- 方法二:滑动窗口
- 其他语言
- python3+哈希表
- python3+滑动窗口
- 写在最后
Tag
【哈希表】【滑动窗口】【数组】
题目来源
219. 存在重复元素 II

题目解读
判断在数组中有没有相同的元素小于一定的距离。
解题思路
方法一:哈希表
我们维护一个哈希表来记录数组中的元素以及上一次出现的位置,如果上一次出现的位置和这一次出现的位置之差小于等于 k,那就返回 true,否则返回 false。
实现代码
class Solution {
public:bool containsNearbyDuplicate(vector<int>& nums, int k) {int n = nums.size();unordered_map<int, int> mp;for (int i = 0; i < n; ++i) {if (mp.count(nums[i]) && (i - mp[nums[i]] <= k)) {return true;}mp[nums[i]] = i;}return false;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 为数组 nums 的长度。
空间复杂度: O ( n ) O(n) O(n),使用哈希表记录数组中元素上一次出现的位置。
方法二:滑动窗口
换一个思路,我们只要判断在长度为 k 的窗口中是否有重复的元素出现即可。在滑窗没满之前,就向滑窗中加入元素,加入之前判断滑窗内是否有当前要加入的元素,如果有,直接返回 false;当滑窗满了,滑动滑窗,当前的 nums[i] 要进入滑窗,那么 nums[i - k - i] 要退出滑窗,判断滑窗内是否有当前要加入的元素,如果有,直接返回 false。
如果滑窗滑到数组末尾,都没有返回 true,就返回 false。
实现代码
class Solution {
public:bool containsNearbyDuplicate(vector<int>& nums, int k) {unordered_set<int> s;int n = nums.size();for (int i = 0; i < n; ++i) {if (i > k) {s.erase(nums[i - k - 1]);}if (s.count(nums[i])) return true;s.emplace(nums[i]);}return false;}
};
时间复杂度: O ( n ) O(n) O(n), n n n 为数组 nums 的长度。
空间复杂度: O ( k ) O(k) O(k),使用无序集合记录滑窗中的元素。
其他语言
python3+哈希表
class Solution:def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:pos = {}for i, num in enumerate(nums):if num in pos and i - pos[num] <= k:return Truepos[num] = ireturn False
python3+滑动窗口
class Solution:def containsNearbyDuplicate(self, nums: List[int], k: int) -> bool:s = set()for i, num in enumerate(nums):if i > k:s.remove(nums[i - k - 1])if num in s:return Trues.add(num)return False
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【面试经典150 | 哈希表】存在重复元素 II
文章目录 Tag题目来源题目解读解题思路方法一:哈希表方法二:滑动窗口 其他语言python3哈希表python3滑动窗口 写在最后 Tag 【哈希表】【滑动窗口】【数组】 题目来源 219. 存在重复元素 II 题目解读 判断在数组中有没有相同的元素小于一定的距离。 解…...
Intellij 安装配置 lombok
Intellij 安装配置 lombok 用 lombok 能够减少 setter/getter/noArgsConstructor 这样的 boilerplate 代码,所以用起来还是比较方便的。 刚开始以为直接安装到 maven 里面就能用了,运行的时候发现 Getter, Data 这些 annotation 根本找不到,…...

Chrome插件精选 — 暗色主题插件
Chrome实现同一功能的插件往往有多款产品,逐一去安装试用耗时又费力,在此为某一类型插件记录下比较好用的一款或几款,便于节省尝试的时间和精力。 Dark Reader 下载地址 (访问密码: 8276) Dark Reader是一款浏览器扩展程序,用于…...
PXE解决uefi安装centos6黑屏问题
解决pxe安装centos6黑屏 author: 铁乐与猫 date:2021.12.10 背景 主板:supermicr SBI-4129P-T3N System InformationManufacturer: SupermicroProduct Name: SBI-4129P-T3NVersion: 123456789Serial Number: S264322X9905439UUID: 00000000-0000-0000-0000-AC1…...

Feign 调用为何POST不支持同时传入多个SpringQueryMap对象,但是GET方法就支持?
Feign 调用为何POST不支持同时传入多个SpringQueryMap对象,但是GET方法就支持? 1.1 问题背景1.2 原因分析1.3 修复方案1.3.1 修复方案一 切换使用GET方法,可以试用多个SpringQueryMap注解 (测试实际不行)1.3.2 修复方案…...
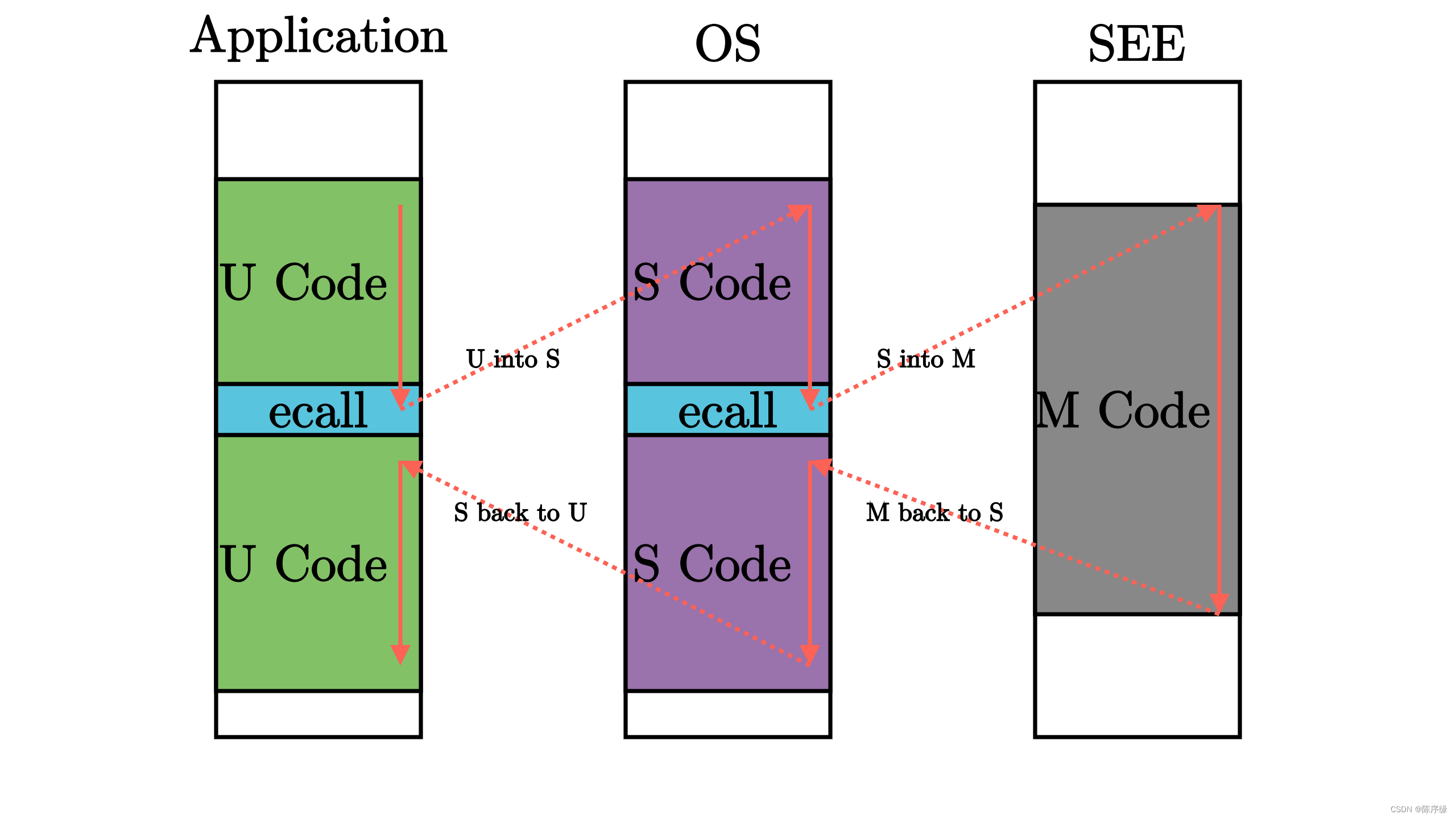
RISC-V 特权级架构
特权级别 级别的数值越大,特权级越高,掌控硬件的能力越强,在CPU硬件层面,M模式必须存在,其它模式可以不存在 执行环境调用 ecall ,这是一种很特殊的陷入类的指令, 相邻两特权级软件之间的接口正…...

目录启示:PHP 与命名空间的声明
文章目录 参考环境命名空间概念版本支持影响范围 全局命名空间概念魔术常量 \_\_NAMESPACE\_\_声明全局命名空间 声明命名空间为空间命名命名规则核心命名空间 子命名空间的声明在同一文件中定义多个命名空间无括号命名空间声明有括号命名空间声明禁止混合使用推荐使用有括号命…...
)
D. Divide and Equalize--Codeforces Round 903 (Div. 3)
D. Divide and Equalize 题意:让一组数中的一个数除以一个因子,一个数除以一个因子,假如经过若干次操作后能够使数组所有数相等,那么输出YES,否则输出NO。 分析:乘除因子,那么实际上就是因子的…...

保姆式教程:MAC安装Android studio(包括安装JDK,Android SDK),解决gradle下载慢的问题
文章目录 参考文章安装JDK并配置环境变量安装JDK配置JDK相关的环境变量 Android studio 安装下载Android studiogradle下载慢解决方法 安装Android SDK选择jdk版本安装SDK并配置环境变量 参考文章 原文链接 原文链接 安装JDK并配置环境变量 安装JDK 下载地址 下载后双击安装…...

Ps:选区的布尔运算
选区的布尔 Boolean运算指的是选区之间的相加(并集)、相减(差集)以及相交(交集),从而形成一个新的选区。 ◆ ◆ ◆ 使用工具选项栏 在 Ps 中,几乎所有的选区工具的工具选项栏上都有…...
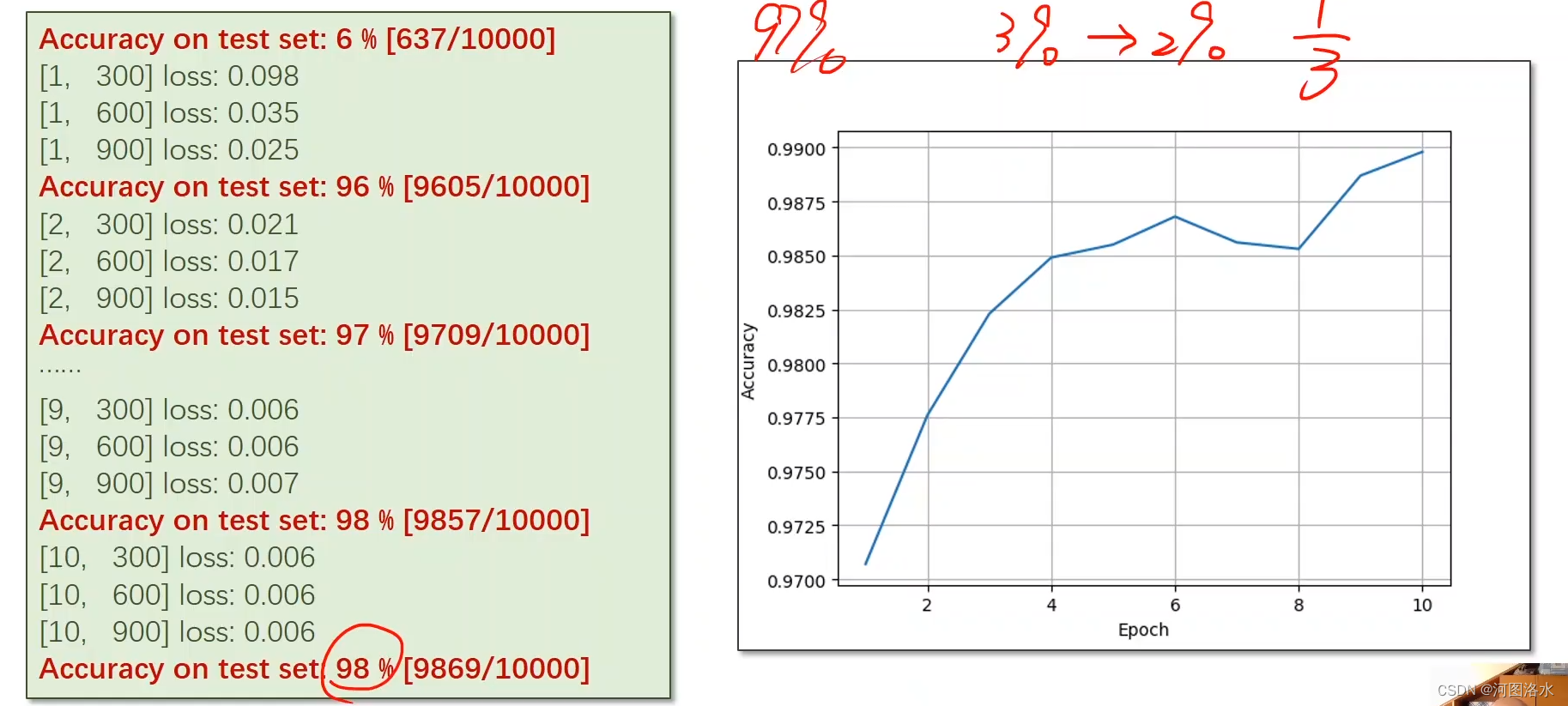
PyTorch 深度学习之卷积神经网络(基础篇)Basic CNN(九)
0. Revision: Fully connected Neural Network 全连接 1. Convolution Neural Network 保留空间信息 1.1 Convolution Convolution-Single Input Channel 单通道 数乘 3 input Channels 3通道 N input Channels N input Channels and M output channel M 个卷积核 1.2 conv…...
torch实现Gated PixelCNN
文章目录 PixelCNNGated PixelCNN PixelCNN import torch import torch.nn as nn import torch.nn.functional as F# Pixel CNNclass MaskConv2d(nn.Module):def __init__(self, conv_type, *args, **kwags):super().__init__()assert conv_type in (A, B)self.conv nn.Conv2…...

破局「二次创业」:合思的新解法
在新的水温下,寻找更为良性的发展正在成为企业的必答题。对此,合思给出的不仅是一份更“省”的答题方法。也更是从认知层到行动层,最后到工具层的一张授人以渔的“渔网”。 作者|思杭 编辑|皮爷 出品|产业家 今年4月初,广州…...
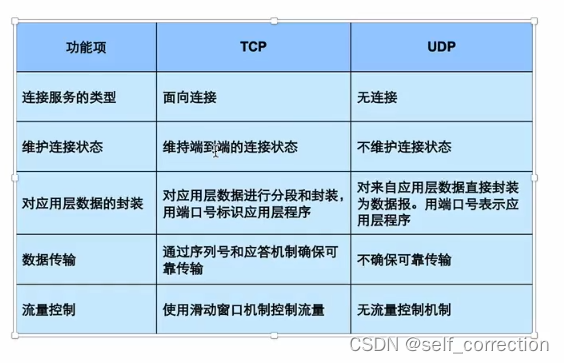
第五章:TCP和UDP基本原理
TCP和UDP基本原理 一、TCP/IP传输层的作用二、 端口1.范围2. 服务端3. 客户端4. 常见知名端口号4.1 TCP 80 HTTP4.2 TCP 20 21 FTP4.3 TCP 23 TELNET4.4 TCP 25 SMTP4.5 UDP 53 DNS4.6 TCP 443 HTTPS 三、 TCP原理1. TCP头部封装格式1.1 Source Port 源端口1.2 Destination Por…...

算法:动态规划的入门理解
文章目录 算法原理题目解析第n个泰波那契数列三步问题使用最小花费爬楼梯 从本篇开始总结的是动态规划的一些内容,动态规划是算法中非常重要的一个版块,因此也是学习算法中的一个重点,在学习动态规划前应当要把动态规划的基础知识学习一下 算…...

最新版nacos 2.2.3服务注册与发现版本依赖问题
最新版nacos的注册服务时配置文件写的是对的,但就是在nacos web页面无法看见服务,此时你需要注意你的依赖是否正确 spring: application:name: orderservicecloud:nacos:discovery:server-addr: 122.51.115.127:8848父工程依赖:现在最新的s…...
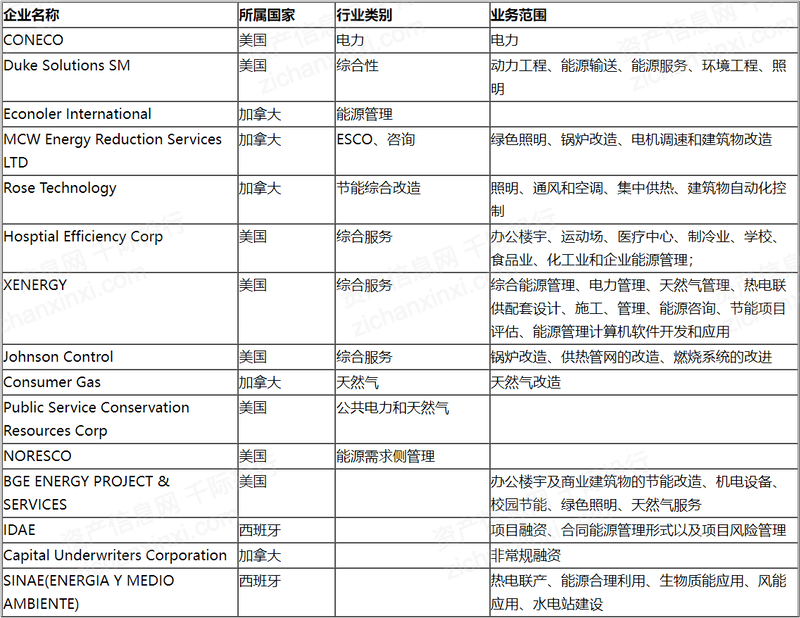
2023年中国合同能源管理行业研究报告
第一章 行业概况 1.1 定义及分类 合同能源管理 (Energy Performance Contracting, EPC) 是当前能源行业中一个重要的概念,它构建了一个桥梁,将节能服务公司 (Energy Management Company, EMCo) 与用能单位紧密联系在一起。通过特定的契约形式ÿ…...

php以半小时为单位,输出指定的时间范围
//可预订小时范围$hour [];for ($i$startHour*3600;$i<$endHour*3600;$i1800){//以半小时为单位输出$startHourItem date(H:i,strtotime(date(Y-m-d))$i);//小时开始$endHourItem date(H:i,strtotime(date(Y-m-d))$i1800);//当前时间再加半小时$hourItemStr $startHourI…...

Electron应用的 asar 打包 解压
前言: .asar文件是一种归档文件格式,通常用于封装Electron应用程序的资源。Electron是一个使得开发者能够使用Web技术构建跨平台桌面应用程序的框架。为了提高性能和简化部署,Electron应用程序的资源通常会被打包到一个.asar文件中。 安装 as…...

蓝桥等考Python组别十七级003
第一部分:选择题 1、Python L17 (15分) 运行下面程序,输出的结果是( )。 def func(x, y): return (x + y) // 3 print(func(7, 5)) 2468正确答案:B 2、Python L17 (15</...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
