Open Winding-PMSM-开绕组永磁同步电机基本介绍
文章目录
- 前言
- 简介
- Open Widing电机数学模型
- 零序模型
- 双逆变器调制
- 零序电流抑制基本思路
前言
最近看了些Open Winding永磁同步电机及其控制策略的文献资料,现做个总结。未来的研究方向也大概率围绕Open Winding开展,期待同行交流学习。
简介
开绕组(Open Winding)电机指把传统的交流电机的三相定子绕组的中性点X/Y/Z打开,这样具有六个接线端子结构的电机即开绕组电机。这样的结构的电机具有高直流电压利用率、更好的容错性能、多电平调制和高转矩密度的优点,因而广泛应用于电动汽车动力系统以及风力发电等场景。
Open Winding电机的驱动拓扑,据逆变器直流侧可以分为隔离直流母线isolated dc bus和共直流母线common dc bus两种类型。
- 隔离直流母线有两个电源,不存在零序通路,因而不必考虑这种拓扑的零序抑制问题。且两个电源的电压等级可以不同,因而存在更多控制的灵活性。缺点在于系统的体积会较共直流母线的拓扑更为庞大。
- 共直流母线的拓扑只有一个电源,存在零序通路,但该种拓扑结构更为简洁,能量密度更高,因而大多数的研究均围绕common dc bus开展,主要研究零序电流的抑制。
从个人观点来看,共直流母线确实更吸引我,至今阅读的文献也都是共直流母线的拓扑,下文提及的Open Winding电机的拓扑均为共直流母线拓扑。
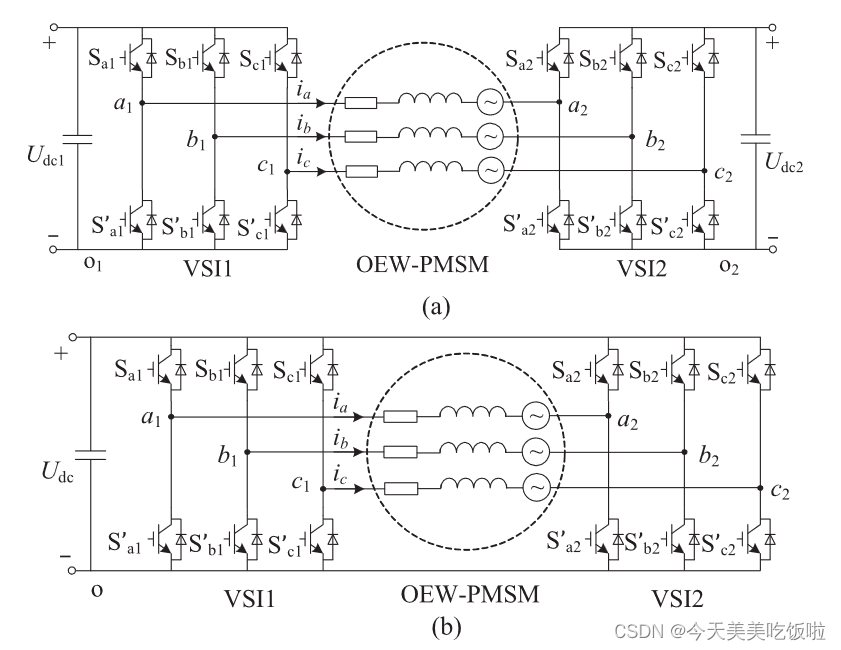
Open Widing电机数学模型
在abc坐标系下Open Winding电机的数学模型与传统的三相电机的数学模型完全相同,唯一不同在于需要考虑零序的影响。因此经park变换到旋转坐标系以后,零序分量不能忽略,必须加以考虑。
旋转坐标系下的电压方程以及转矩方程为:
[ u d u q u 0 ] \begin{bmatrix} u_d\\ u_q\\ u_0 \end{bmatrix} uduqu0 = [ p L d + R s p L q + R s p L 0 + R s ] \begin{bmatrix} pL_d+R_s& &\\ &pL_q+R_s&\\ &&pL_0+R_s \end{bmatrix} pLd+RspLq+RspL0+Rs [ i d i q i 0 ] \begin{bmatrix} i_d\\ i_q\\ i_0 \end{bmatrix} idiqi0 + [ 0 ω e ψ f 1 − 3 ω e ψ f 3 s i n ( 3 θ e ) ] \begin{bmatrix} 0\\ \omega_e\psi_{f1}\\ -3\omega_e\psi_{f3}sin(3\theta_e) \end{bmatrix} 0ωeψf1−3ωeψf3sin(3θe)
T e = 3 2 n p [ i q ψ f 1 + ( L d − L q ) i d i q − 6 i 0 ψ f 3 s i n ( 3 θ e ) ] T_e=\frac{3}{2}n_p[i_q\psi_{f1}+(L_d-L_q)i_di_q-6i_0\psi_{f3}sin(3\theta_e)] Te=23np[iqψf1+(Ld−Lq)idiq−6i0ψf3sin(3θe)]
其中, L d , L q , L 0 L_d,L_q,L_0 Ld,Lq,L0分别为d/q/0轴的等效电感, R s R_s Rs为每相绕组的等效电阻, ω e \omega_e ωe为电机电旋转角速度, ψ f 1 , ψ f 3 \psi_{f1},\psi_{f3} ψf1,ψf3分别为永磁体的磁链的基波分量以及三次谐波分量。记 e 0 = − 3 ω e ψ f 3 s i n ( 3 θ e ) e_0=-3\omega_e\psi_{f3}sin(3\theta_e) e0=−3ωeψf3sin(3θe),称 e 0 e_0 e0为Open Winding电机的零序反电动势。
从转矩方程可以看出,与传统的PMSM电机的转矩方程相比,多出了零序电流的贡献部分,且该部分正比于永磁体磁链的三次谐波以及与三倍电角度的正弦值有关。常规的永磁电机在制造时,通常有意保留永磁体的三次谐波谐波来提高电机的转矩密度,因此 ψ f 3 ≠ 0 \psi_{f3}\neq0 ψf3=0,因此零序电流的存在会显著影响电磁转矩,从而造成转矩脉动。这是共直流母线电压最为显著的问题,因而绝大多数共直流母线开绕组电机的研究均围绕零序电流的抑制开展。
零序模型
从零序电压方程中可以看出, u 0 = R s i 0 + L 0 d i 0 d t + e 0 u_0=R_si_0+L_0\frac{di_0}{dt}+e_0 u0=Rsi0+L0dtdi0+e0,因此可以画出零序等效电路。
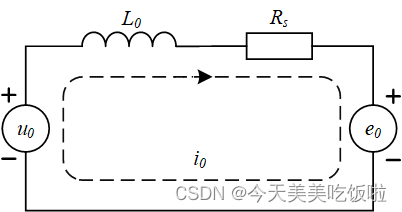
显然零序等效电路中有两个电压源,分别为 u 0 , e 0 u_0,e_0 u0,e0。其中 u 0 u_0 u0是逆变器经调制施加到OpenWinding电机机端上等效的零序电压(Zero Sequence Voltage,ZSV),在一些文献中也称为共模电压(Common Mode Voltage, CMV); e 0 e_0 e0是电机的零序反电动势,根据dq0坐标系下的电压方程可知, e 0 = − 3 ω e ψ f 3 s i n ( 3 θ e ) e_0=-3\omega_e\psi_{f3}sin(3\theta_e) e0=−3ωeψf3sin(3θe),是一个与磁链的三次谐波以及三倍电角度正弦值有关的变量。而前文已提到电机制造时会有意保留磁链的三次谐波,因此 ψ f 3 ≠ 0 \psi_{f3}\neq0 ψf3=0, e 0 e_0 e0不会恒为0。
因此若要达到消除或抑制零序电流 i 0 i_0 i0的效果,只能从共模电压 u 0 u_0 u0入手,施加一定的控制,使得 u 0 ≈ e 0 u_0\approx e_0 u0≈e0,从而抑制零序电流 i 0 i_0 i0。
双逆变器调制
由于Open Winding将电机绕组中性点X/Y/Z打开,可以将ABC三相绕组的一端a1,b1,c1接入逆变器1,而三相绕组的另一端a2,b2,c2接入逆变器2,为了使得电机的正常运行,做到两个逆变器的电压矢量,分别记为 u s 1 , u s 2 u_{s1},u_{s2} us1,us2合称为一个矢量圆 u s u_s us即可。
根据传统电机电压矢量,两个逆变器的电压矢量可以用下图表示,其中左图为逆变器1的电压矢量 u s 1 u_{s1} us1,右图为逆变器2的电压矢量 u s 2 u_{s2} us2。
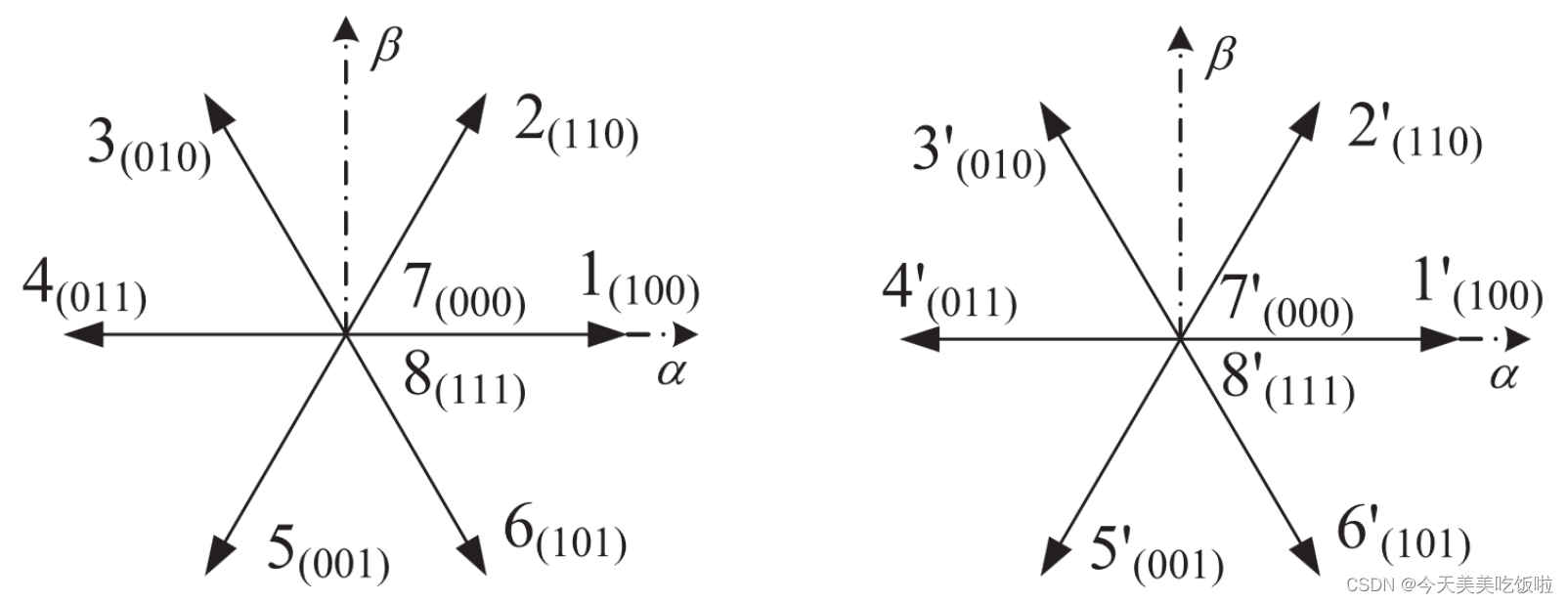
根据开绕组电机的特性,施加到开绕组电机上的合成电压矢量 u s = u s 1 − u s 2 u_s=u_{s1}-u_{s2} us=us1−us2,即用左图的电压矢量减去有图的电压矢量,得到的结果即双逆变器调制的电压矢量分布,结果如下图所示。
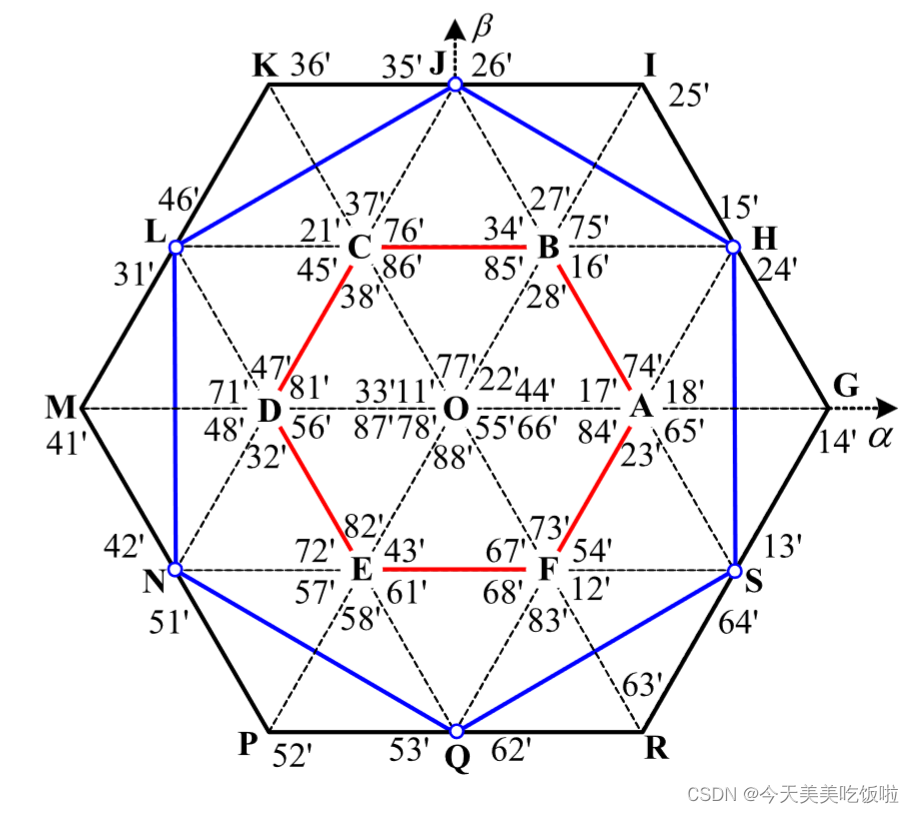
由最终的合成电压矢量图可以看出,双逆变器调制有三种六边形调制方式:
- 六边形ABCDEF,也称为内六边形调制,直流电压利用率最低,几乎不采用该种调制方式
- 六边形HJLNQS,也称为中间六边形调制,120度解耦调制,直流电压利用率较高,且不会因为调制产生共模电压。
- 六边形GIKMPR,也称为最大六边形调制,180度解耦调制,直流电压利用率最高,但会因为调制产生共模电压。
还有其他的调制方式,比如六边形钳位,但相较于前面提及的120度解耦调制与180度解耦调制相比实现方式更为复杂。
零序电流抑制基本思路
回到上文提到的内容,开绕组电机控制的首要目标是抑制零序电流,从零序等效电路模型出发,即需要灵活的控制由逆变器调制引起的共模电压CMV近似跟踪零序反电动势。120度解耦调制不会引入共模电压,即 u 0 ≡ 0 u_0\equiv0 u0≡0,零序电路中只有零序反电动势,具有非常大的零序环流;180度解耦会引入共模电压,但共模电压完全取决于SVPWM调制发波引入,不施加一定的控制,并不能做到 u 0 ≈ e 0 u_0\approx e_0 u0≈e0,同样不能抑制零序环流。
传统的SVPWM只需要根据两相静止坐标系下的 u α , u β u_{\alpha},u_{\beta} uα,uβ即可生成SVPWM,为了使得SVPWM调制出的共模电压可控,需要另外引入一个控制变量 u 0 u_0 u0,进而调节零矢量的调节时间,达到调制出的共模电压可控的效果。而这种引入第三个控制变量的SVPWM多用于开绕组电机的零序电流抑制,在多数文献中也称为三维调制。引入的控制变量 u 0 u_0 u0为零序电压指令值,由零序电流控制器产生,通常设置为PI或者PR控制器。
相关文章:

Open Winding-PMSM-开绕组永磁同步电机基本介绍
文章目录 前言简介Open Widing电机数学模型零序模型 双逆变器调制零序电流抑制基本思路 前言 最近看了些Open Winding永磁同步电机及其控制策略的文献资料,现做个总结。未来的研究方向也大概率围绕Open Winding开展,期待同行交流学习。 简介 开绕组(O…...
uniapp 一次性上传多条视频 u-upload accept=“video“ uni.chooseMedia uni.uploadFile
方式 一 部分安卓机 只能一条一条传视频 文档地址 uview 2.0 Upload 上传组件 html <view class"formupload"><u-upload accept"video":fileList"fileList3" afterRead"afterRead" delete"deletePic" name"…...

CentOS7卸载硬盘报错:umount: /data: target is busy.
问题描述 umount: /data: target is busy. 问题分析 硬盘正在被使用,不能被卸载。 解决方案 查看哪些程序在使用硬盘 [rootlocalhost ~]# lsof /data/ COMMAND PID USER FD TYPE DEVICE SIZE/OFF NODE NAME mysqld 15655 polkitd cwd …...
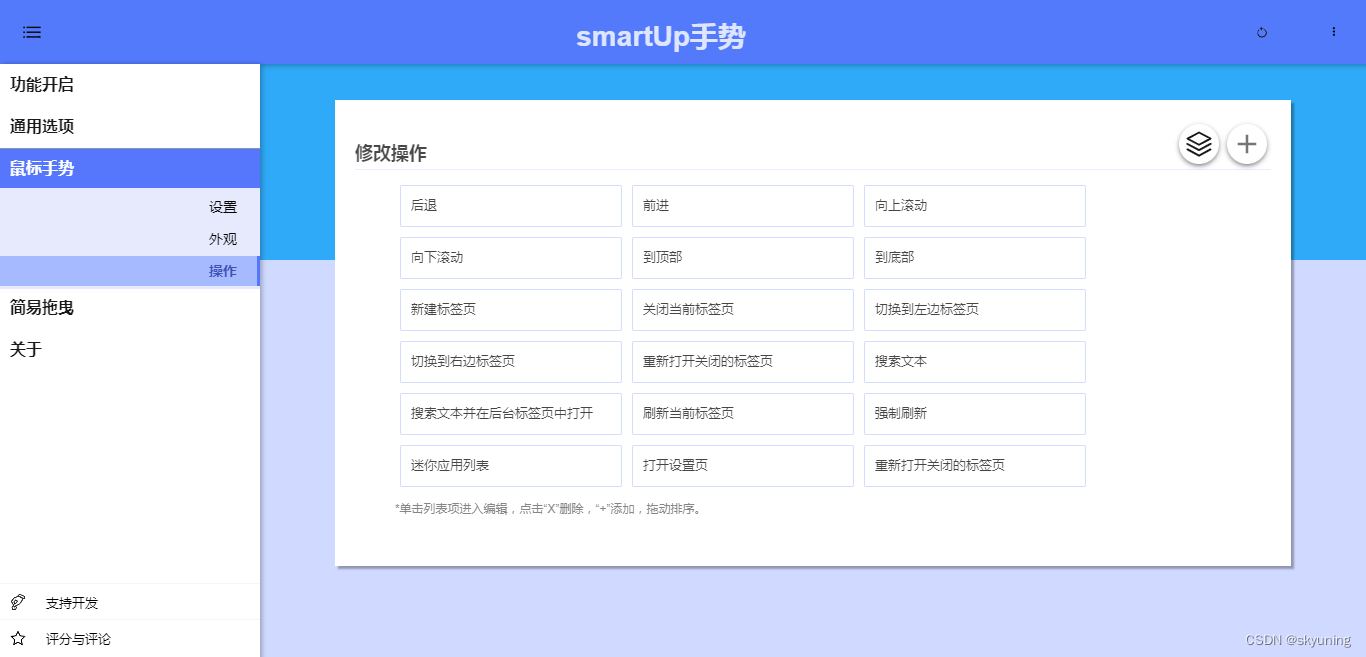
Chrome插件精选 — 鼠标手势插件
Chrome实现同一功能的插件往往有多款产品,逐一去安装试用耗时又费力,在此为某一类型插件记录下比较好用的一款或几款,便于节省尝试的时间和精力。 下面是两款比较好用的鼠标手势插件,支持很多设置选项,可以自定义手势&…...

JMeter分布式
一 分布式注意事项 关闭防火墙控制机和代理机在同一子网控制机和代理机上安装的jmeter和JDK版本要一样关闭jmeter的RMI SSL开关 二 代理机(agent)的配置 修改服务端口 打开bin/jmeter.properties文件,修改’server_port’ 将RMI SSL设备…...
[华为杯研究生创新赛 2023] 初赛 REV WP
前言 一年没打比赛了, 差一题进决赛, REV当时lin的第三个challenge没看出来是凯撒, 想得复杂了, 结果错失一次线下机会 >_< T4ee 动态调试, nop掉反调试代码 发现处理过程为 置换sub_412F20处理(这里看其他师傅的wp知道应该是rc4, 我是直接en逆的buf字符串中每一位和…...

C++中resize和reserve
1.reserve(n)对capacity操作 capacity < n : 扩容capacity > n : 不操作 2.resize(n, m)对size操作 size < n : size增加到n 增加的值为msize > n : size减小到ncapacity < n : 先增大容量至n 再增大size至n 增加的值为m...

【面试经典150 | 哈希表】存在重复元素 II
文章目录 Tag题目来源题目解读解题思路方法一:哈希表方法二:滑动窗口 其他语言python3哈希表python3滑动窗口 写在最后 Tag 【哈希表】【滑动窗口】【数组】 题目来源 219. 存在重复元素 II 题目解读 判断在数组中有没有相同的元素小于一定的距离。 解…...
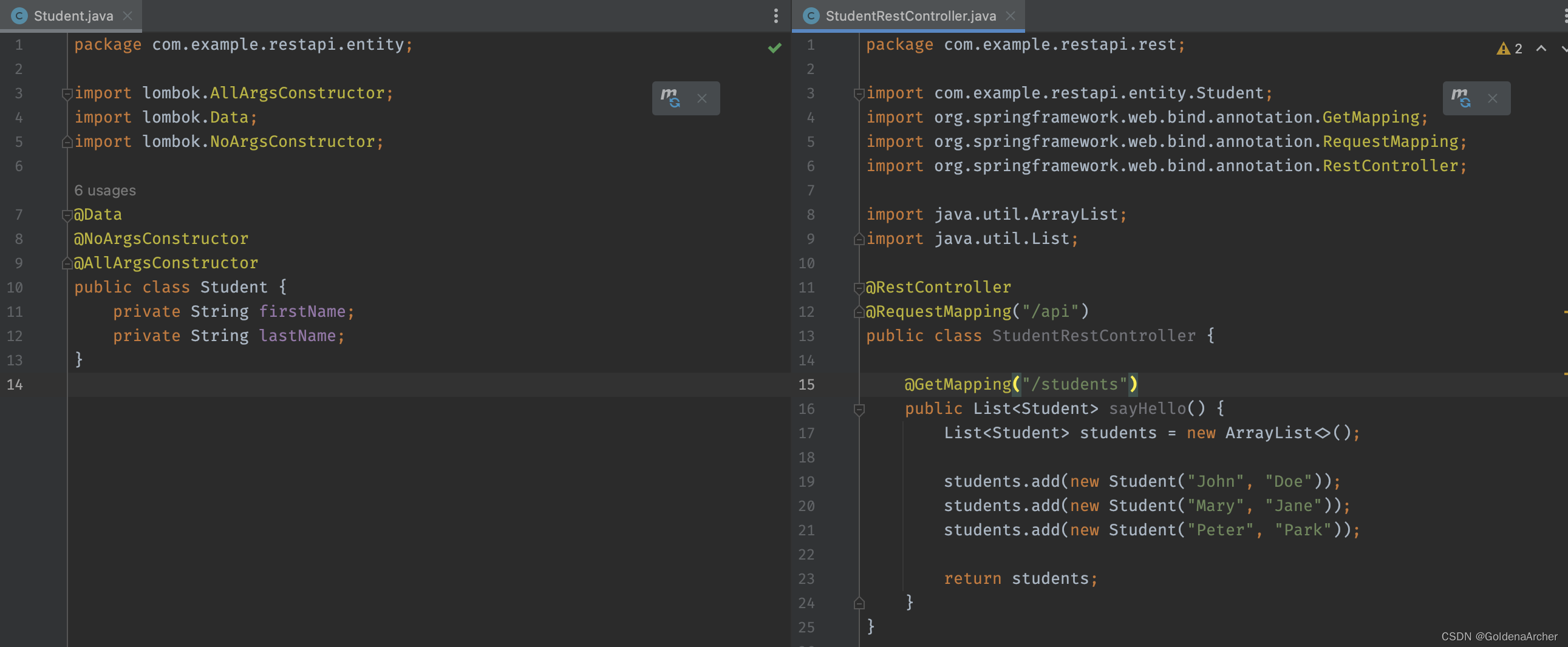
Intellij 安装配置 lombok
Intellij 安装配置 lombok 用 lombok 能够减少 setter/getter/noArgsConstructor 这样的 boilerplate 代码,所以用起来还是比较方便的。 刚开始以为直接安装到 maven 里面就能用了,运行的时候发现 Getter, Data 这些 annotation 根本找不到,…...

Chrome插件精选 — 暗色主题插件
Chrome实现同一功能的插件往往有多款产品,逐一去安装试用耗时又费力,在此为某一类型插件记录下比较好用的一款或几款,便于节省尝试的时间和精力。 Dark Reader 下载地址 (访问密码: 8276) Dark Reader是一款浏览器扩展程序,用于…...
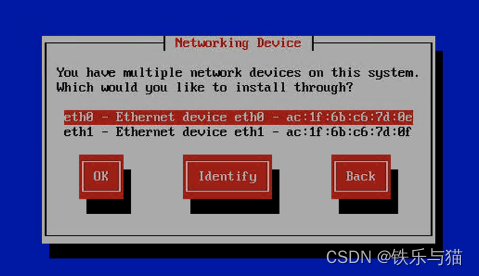
PXE解决uefi安装centos6黑屏问题
解决pxe安装centos6黑屏 author: 铁乐与猫 date:2021.12.10 背景 主板:supermicr SBI-4129P-T3N System InformationManufacturer: SupermicroProduct Name: SBI-4129P-T3NVersion: 123456789Serial Number: S264322X9905439UUID: 00000000-0000-0000-0000-AC1…...

Feign 调用为何POST不支持同时传入多个SpringQueryMap对象,但是GET方法就支持?
Feign 调用为何POST不支持同时传入多个SpringQueryMap对象,但是GET方法就支持? 1.1 问题背景1.2 原因分析1.3 修复方案1.3.1 修复方案一 切换使用GET方法,可以试用多个SpringQueryMap注解 (测试实际不行)1.3.2 修复方案…...
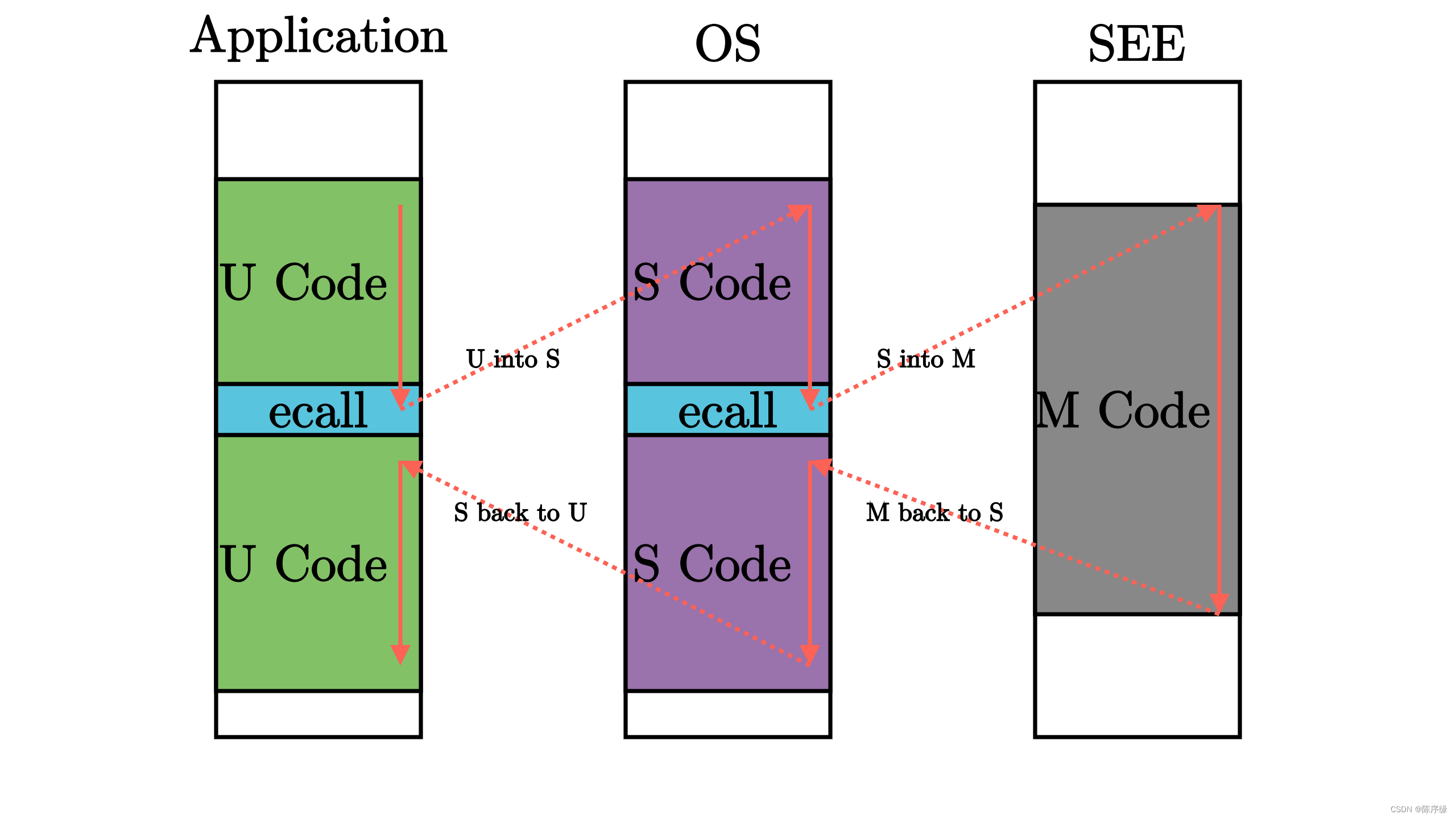
RISC-V 特权级架构
特权级别 级别的数值越大,特权级越高,掌控硬件的能力越强,在CPU硬件层面,M模式必须存在,其它模式可以不存在 执行环境调用 ecall ,这是一种很特殊的陷入类的指令, 相邻两特权级软件之间的接口正…...

目录启示:PHP 与命名空间的声明
文章目录 参考环境命名空间概念版本支持影响范围 全局命名空间概念魔术常量 \_\_NAMESPACE\_\_声明全局命名空间 声明命名空间为空间命名命名规则核心命名空间 子命名空间的声明在同一文件中定义多个命名空间无括号命名空间声明有括号命名空间声明禁止混合使用推荐使用有括号命…...
)
D. Divide and Equalize--Codeforces Round 903 (Div. 3)
D. Divide and Equalize 题意:让一组数中的一个数除以一个因子,一个数除以一个因子,假如经过若干次操作后能够使数组所有数相等,那么输出YES,否则输出NO。 分析:乘除因子,那么实际上就是因子的…...

保姆式教程:MAC安装Android studio(包括安装JDK,Android SDK),解决gradle下载慢的问题
文章目录 参考文章安装JDK并配置环境变量安装JDK配置JDK相关的环境变量 Android studio 安装下载Android studiogradle下载慢解决方法 安装Android SDK选择jdk版本安装SDK并配置环境变量 参考文章 原文链接 原文链接 安装JDK并配置环境变量 安装JDK 下载地址 下载后双击安装…...

Ps:选区的布尔运算
选区的布尔 Boolean运算指的是选区之间的相加(并集)、相减(差集)以及相交(交集),从而形成一个新的选区。 ◆ ◆ ◆ 使用工具选项栏 在 Ps 中,几乎所有的选区工具的工具选项栏上都有…...
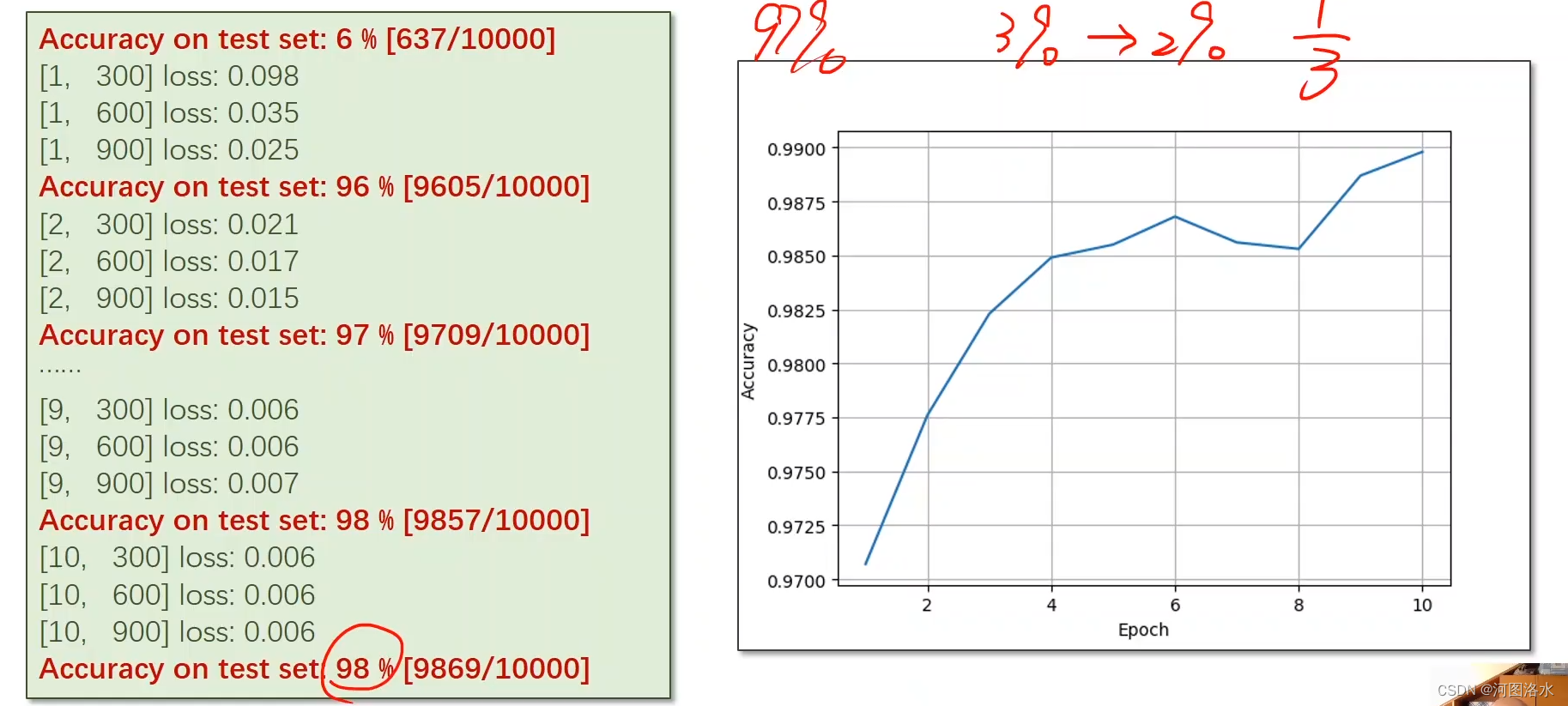
PyTorch 深度学习之卷积神经网络(基础篇)Basic CNN(九)
0. Revision: Fully connected Neural Network 全连接 1. Convolution Neural Network 保留空间信息 1.1 Convolution Convolution-Single Input Channel 单通道 数乘 3 input Channels 3通道 N input Channels N input Channels and M output channel M 个卷积核 1.2 conv…...
torch实现Gated PixelCNN
文章目录 PixelCNNGated PixelCNN PixelCNN import torch import torch.nn as nn import torch.nn.functional as F# Pixel CNNclass MaskConv2d(nn.Module):def __init__(self, conv_type, *args, **kwags):super().__init__()assert conv_type in (A, B)self.conv nn.Conv2…...

破局「二次创业」:合思的新解法
在新的水温下,寻找更为良性的发展正在成为企业的必答题。对此,合思给出的不仅是一份更“省”的答题方法。也更是从认知层到行动层,最后到工具层的一张授人以渔的“渔网”。 作者|思杭 编辑|皮爷 出品|产业家 今年4月初,广州…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
