当前位置： 首页 > news >正文

Android 12.0 hal层添加自定义hal模块功能实现

news 文章来源：https://blog.csdn.net/baidu_41666295/article/details/133778875 2025/4/22 13:10:41

1. 前言

在12.0的系统rom定制化开发中，在 对hal模块进行开发时，需要通过添加自定义的hal模块来实现某些功能时，就需要添加hal模块的相关功能，接下来就来实现一个案例来供参考
接下来就来具体实现这个功能

2.hal层添加自定义hal模块功能实现的核心类

hardware\interfaces\

3.hal层添加自定义hal模块功能实现的核心功能分析和实现


Android系统的硬件抽象层（Hardware Abstract Layer, HAL）运行在用户空间中，它向下屏蔽硬件驱动模块的实现细节，向上提供硬件访问服务。
通过硬件抽象层，Android系统分为两层来支持硬件设备，其中一层实现在用户空间（User Space），另外一层是现在内核空间（Kernel Space）。
传统的Linux系统把对硬件的支持完全是现在在内核空间，即把对硬件的支持完全实现在硬件驱动模块中。

HIDL的全称是HAL interface definition language（硬件抽象层接口定义语言），在此之前Android 有AIDL，
架构在Android binder 之上，用来定义Android 基于Binder通信的Client 与Service之间的接口。
HIDL也是类似的作用，只不过定义的是Android Framework与Android HAL实现之间的接口。

HIDL可以分为：HIDL C++(C++实现)、HIDL Java(Java 实现)，并且还主要分为直通式和绑定式，
本篇文章使用的C+&#

相关文章：

Android 12.0 hal层添加自定义hal模块功能实现

1. 前言 在12.0的系统rom定制化开发中，在 对hal模块进行开发时，需要通过添加自定义的hal模块来实现某些功能时，就需要添加hal模块的相关功能，接下来就来实现一个案例来供参考 接下来就来具体实现这个功能 2.hal层添加自定义hal模块功能实现的核心类 hardware\interfaces…...

编程日记 2023/10/14 10:08:48

如何理解vue声明式渲染

Vue.js中的声明式渲染是一种用来描述用户界面的方式，它强调“声明”应该如何渲染页面，而不需要关心底层的DOM操作。这与传统的命令式渲染方式，即手动控制DOM元素的创建、更新和销毁，形成了鲜明的对比。 理解Vue的声明式渲染的关键…...

编程日记 2023/10/14 10:07:46

【已解决】Vue全局引入scss 个别页面不生效 / 不自动引入全局样式

项目里配置了全局样式的引入，今天新建了 demo 页面去修改 element 的样式，发现全局的样式没有引入进来。 问题原因 在此页面 没有任何样式导致的 项目在编译的时候，会把 .vue 文件的样式抽离到单独的 css 文件中。 当该页面没有css代码的时…...

编程日记 2023/10/14 10:06:44

MySQL之双主双从读写分离

一个主机 Master1 用于处理所有写请求，它的从机 Slave1 和另一台主机 Master2 还有它的从 机 Slave2 负责所有读请求。当 Master1 主机宕机后， Master2 主机负责写请求， Master1 、 Master2 互为备机。架构图如下 : 准备 我们…...

编程日记 2023/10/14 10:05:43

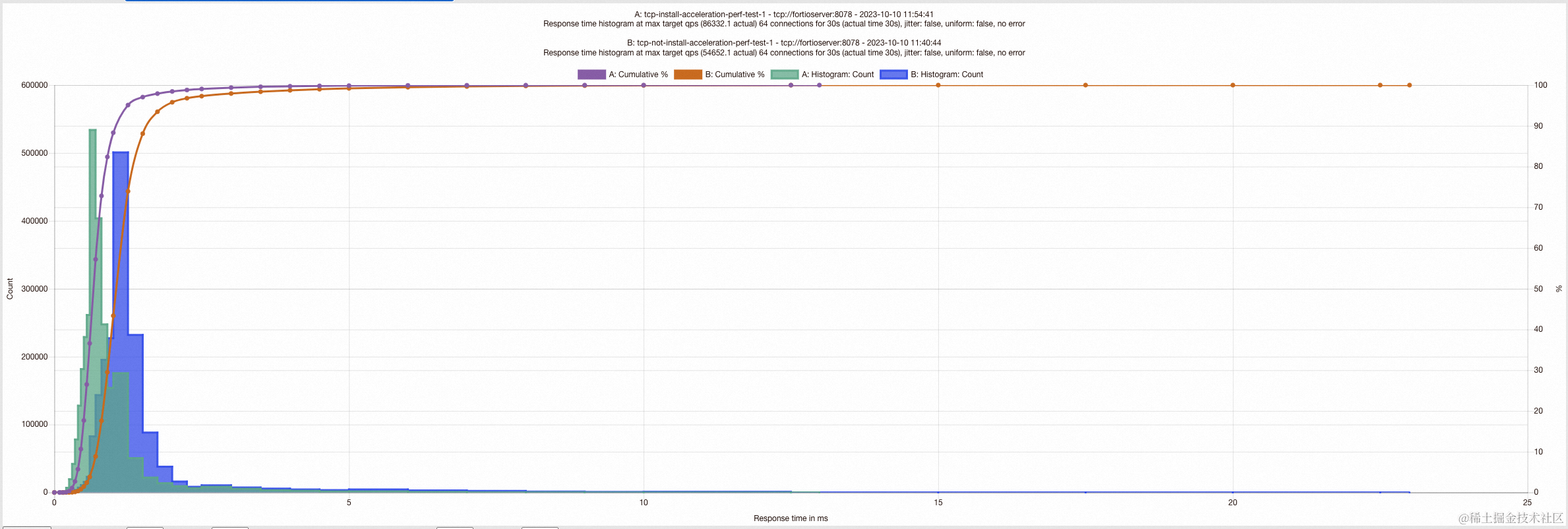
使用eBPF加速阿里云服务网格ASM

背景 随着云原生应用架构的快速发展，微服务架构已经成为了构建现代应用的主要方式之一。而在微服务架构中，服务间的通信变得至关重要。为了实现弹性和可伸缩性，许多组织开始采用服务网格技术来管理服务之间的通信。 Istio作为目前最受欢迎的…...

编程日记 2023/10/14 10:04:43

大型数据集处理之道：深入了解Hadoop及MapReduce原理

在大数据时代，处理海量数据是一项巨大挑战。而Hadoop作为一个开源的分布式计算框架，以其强大的处理能力和可靠性而备受推崇。本文将介绍Hadoop及MapReduce原理，帮助您全面了解大型数据集处理的核心技术。 Hadoop简介 Hadoop是一个基于Google…...

编程日记 2023/10/14 10:03:41

LCR 095. 最长公共子序列（C语言+动态规划）

1. 题目 给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。 一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符&#xff08…...

编程日记 2023/10/14 10:02:40

程序员不写注释：探讨与反思

一、为什么程序员不写注释 当程序员选择不写注释时，通常有一系列常见原因，这些原因可以影响他们的决策和行为。同时，这个决策可能会带来多方面的影响和后果。以下是详细阐述为什么程序员不写注释的常见原因以及这种决策可能导致的影响和后果…...

编程日记 2023/10/14 10:01:39

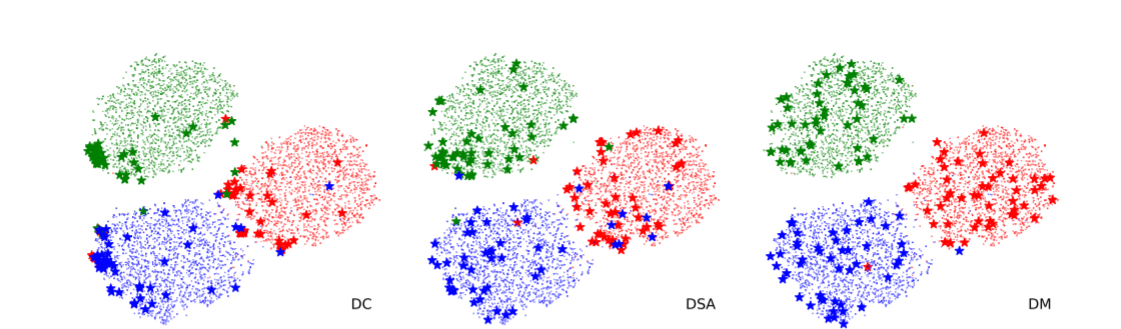
《论文阅读：Dataset Condensation with Distribution Matching》

点进去这篇文章的开源地址，才发现这篇文章和DC DSA居然是一个作者，数据浓缩写了三篇论文，第一篇梯度匹配，第二篇数据增强后梯度匹配，第三篇匹配数据分布。DC是匹配浓缩数据和原始数据训练一次后的梯度差，DS…...

编程日记 2023/10/14 10:00:37

免费chatGPT工具

发现很多人还是找不到好用的chatGPT工具，这里分享一个邮箱注册即可免费试用。 PromptsZone - 一体化人工智能平台使用 PromptsZone 与 ChatGPT、Claude、AI21 Labs、Google Bard 聊天，并使用 DALL-E、Stable Diffusion 和 Google Imagegen 创建图像&…...

编程日记 2023/10/14 9:59:32

数据分析基础:数据可视化+数据分析报告

数据分析是指通过对大量数据进行收集、整理、处理和分析，以发现其中的模式、趋势和关联，并从中提取有价值的信息和知识。 数据可视化和数据分析报告是数据分析过程中非常重要的两个环节，它们帮助将数据转化为易于理解和传达的形式&#xff0…...

编程日记 2023/10/14 9:58:31

settings.xml的文件配置大全

settings.xml 文件中最常配置的还是这几个标签 localRepository和mirrors settings.xml文件官方文档地址 <settings xmlns"http://maven.apache.org/SETTINGS/1.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"ht…...

编程日记 2023/10/14 9:57:29

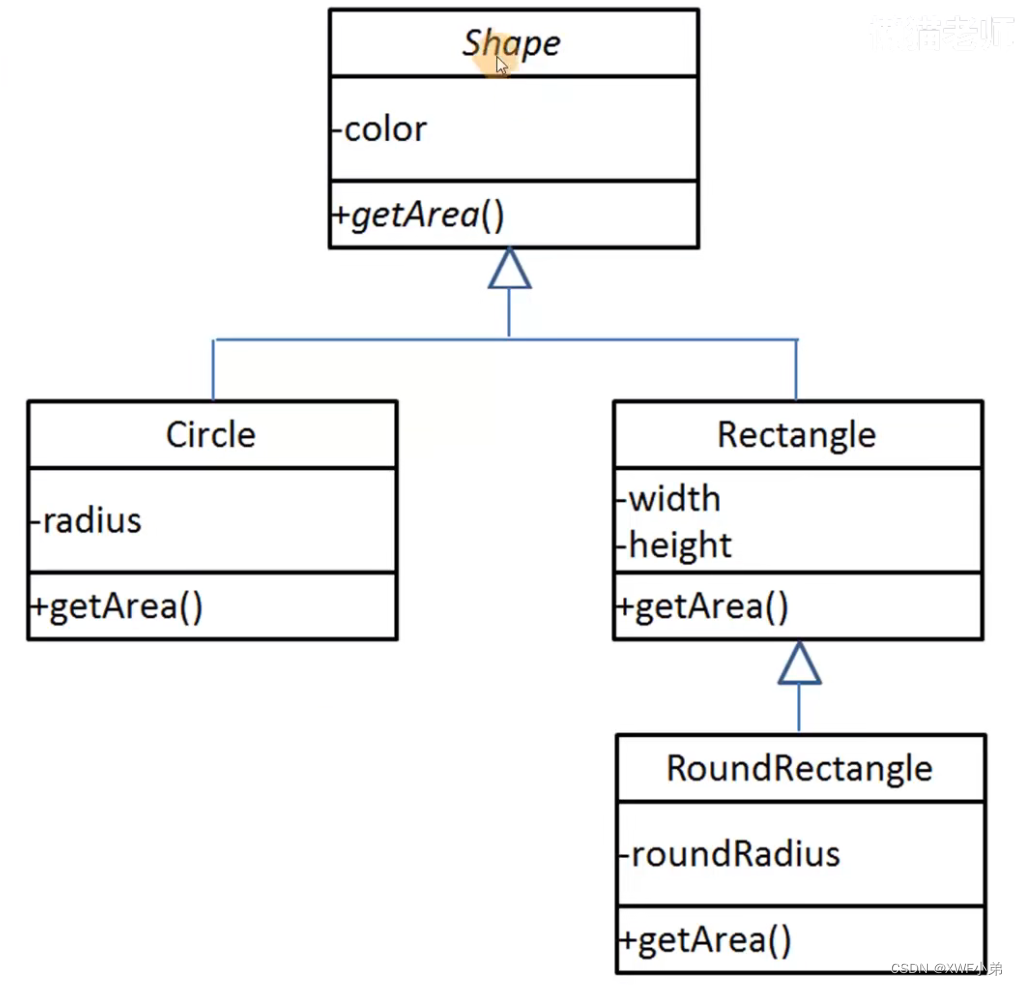
极简c++（7）类的继承

为什么要用继承 子类不必复制父类的任何属性&#xff0c;已经继承下来了&#xff1b;易于维护与编写&#xff1b; 类的继承与派生 访问控制规则 一般只使用Public&#xff01; 构造函数的继承与析构函数的继承 构造函数不被继承&#xff01; 在创建子类对象的时候&…...

编程日记 2023/10/14 9:56:28

DOSBox和MASM汇编开发环境搭建

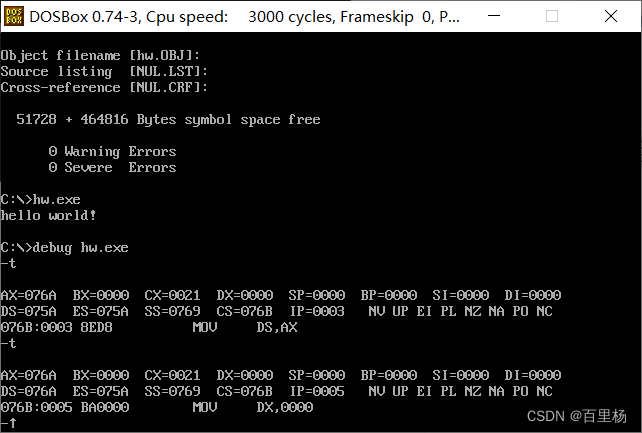
DOSBox和MASM汇编开发环境搭建 1 安装DOSBox2 安装MASM3 编译测试代码4 运行测试代码5 调试测试代码 本文属于《 X86指令基础系列教程》之一&#xff0c;欢迎查看其它文章。 1 安装DOSBox 下载DOSBox和MASM&#xff1a;https://download.csdn.net/download/u011832525/884180…...

编程日记 2023/10/14 9:55:27

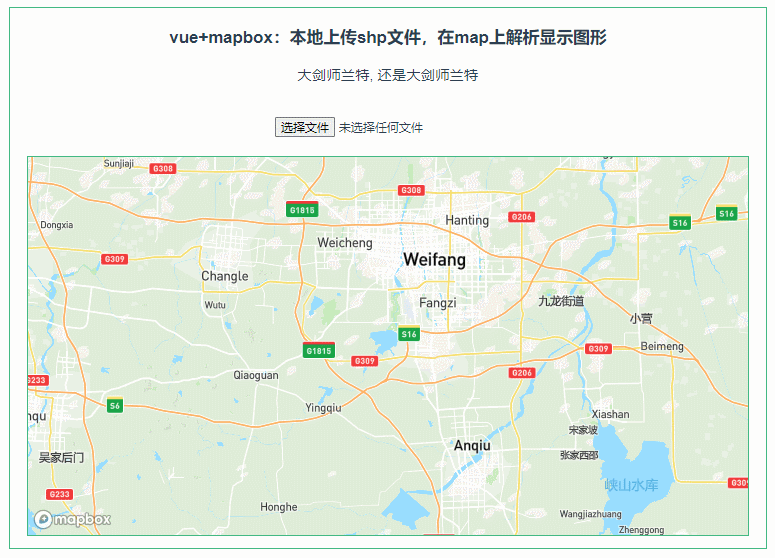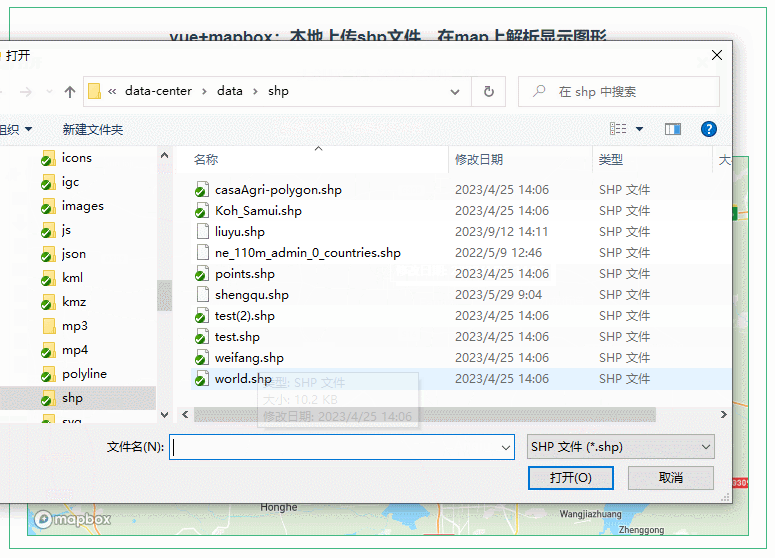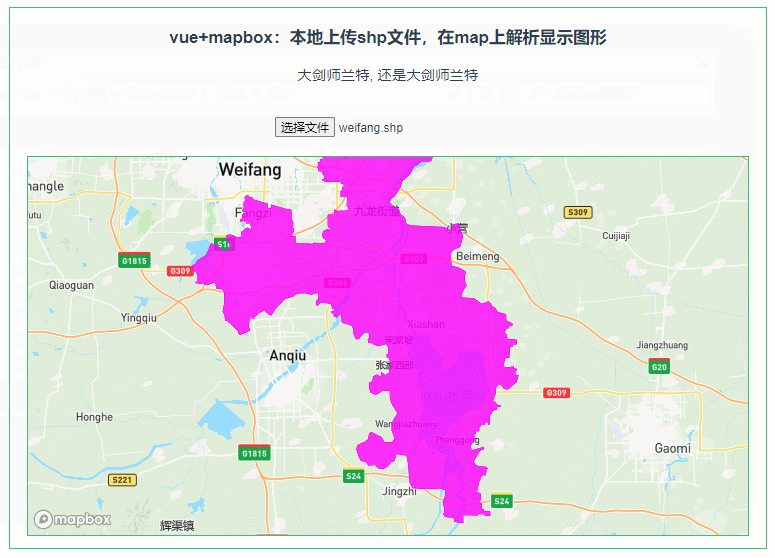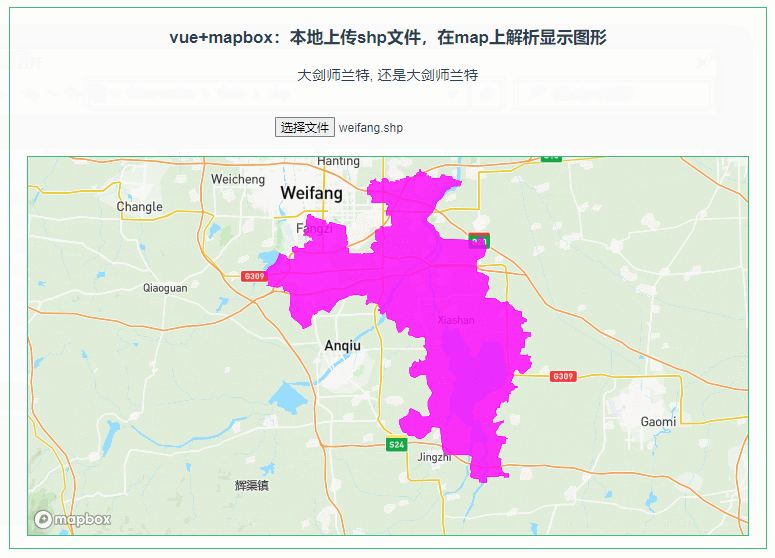
047：mapboxGL本地上传shp文件，在map上解析显示图形

第047个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+mapbox中本地上传shp文件，利用shapefile读取shp数据，并在地图上显示图形。 直接复制下面的 vue+mapbox源代码，操作2分钟即可运行实现效果 文章目录 示例效果配置方式示例源代码（共117行）加载shapefile.js方式…...

编程日记 2023/10/14 9:54:26

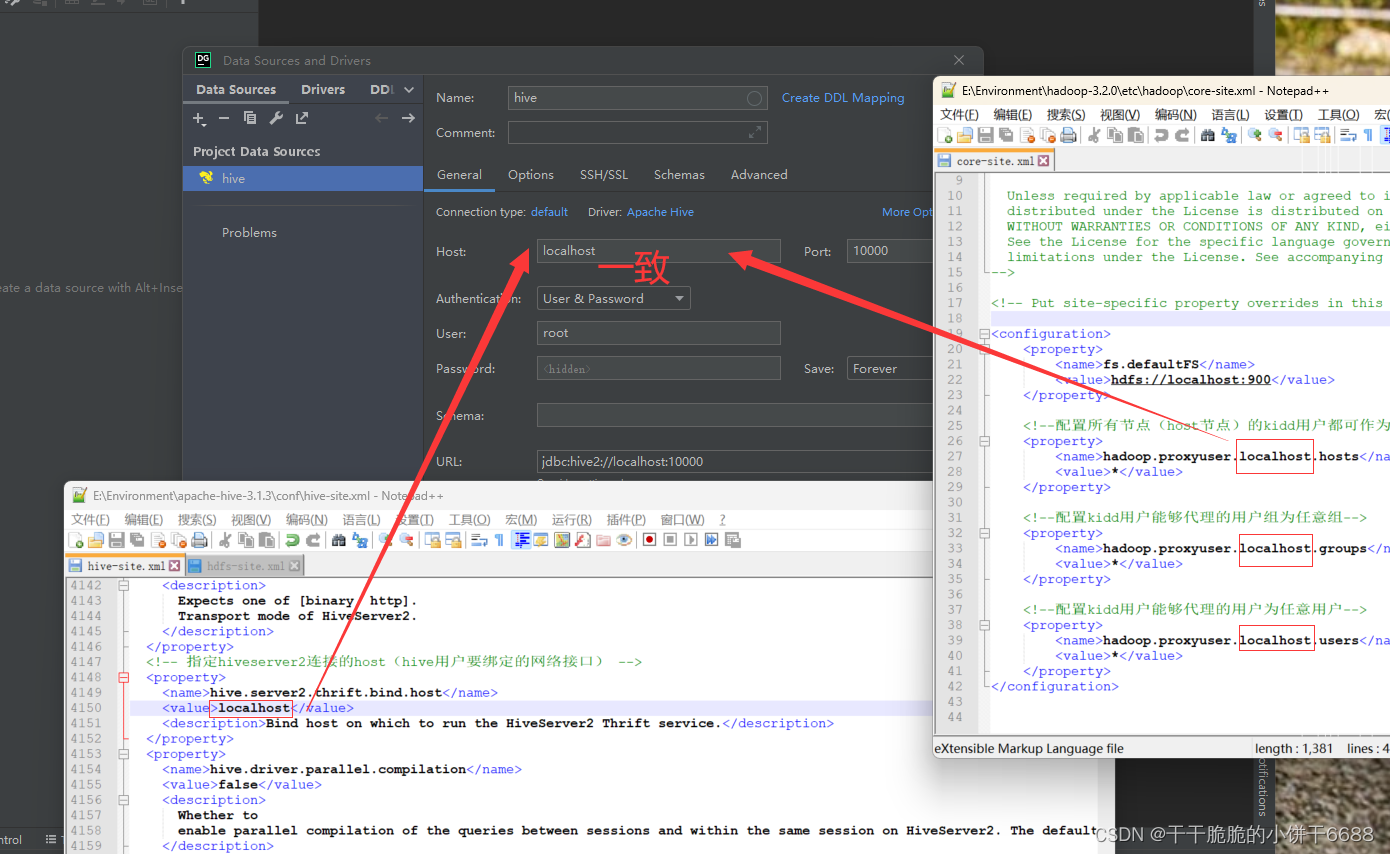
Windows下DataGrip连接Hive

DataGrip连接Hive 1. 启动Hadoop2. 启动hiveserver2服务3. 启动元数据服务4. 启动DG 1. 启动Hadoop 在控制台中输入start-all.cmd后&#xff0c;弹出下图4个终端&#xff08;注意终端的名字&#xff09;2. 启动hiveserver2服务 单独开一个窗口启动hiveserver2服务&#xff0c;…...

编程日记 2023/10/14 9:53:25

Xshell7和Xftp7超详细下载教程（包括安装及连接服务器附安装包）

1.下载 1.官网地址&#xff1a; XSHELL - NetSarang Website 选择学校免费版下载 2.将XSHELL和XFTP全都下载下来 2.安装 安装过程就是选择默认选项&#xff0c;然后无脑下一步 3.连接服务器 1.打开Xshell7&#xff0c;然后新建会话 2.填写相关信息 出现Connection establi…...

编程日记 2023/10/14 9:52:24

ASP.net数据从Controller传递到视图

最常见的方式是使用模型或 ViewBag。 使用模型传递数据&#xff1a; 在控制器中&#xff0c;创建一个模型对象&#xff0c;并将数据赋值给模型的属性。然后将模型传递给 View 方法。 public class HomeController : Controller {public IActionResult Index(){// 创建模型对…...

编程日记 2023/10/14 9:51:23

c++ 友元函数 友元类

1. 友元函数 1.1 简介 友元函数是在类的声明中声明的非成员函数&#xff0c;它被授予访问类的私有成员的权限。这意味着友元函数可以访问类的私有成员变量和私有成员函数&#xff0c;即使它们不是类的成员。 一个类中&#xff0c;可以将其他类或者函数声明为该类的友元&#…...

编程日记 2023/10/14 9:50:22

Spring推断构造器源码分析

Spring中bean虽然可以通过多种方式&#xff08;Supplier接口、FactoryMethod、构造器&#xff09;创建bean的实例对象&#xff0c;但是使用最多的还是通过构造器创建对象实例&#xff0c;也是我们最熟悉的创建对象的方式。如果有多个构造器时&#xff0c;那Spring是如何推断使用…...

编程日记 2023/10/14 9:49:21

十五、【历史记录画笔工具组】

文章目录 历史记录画笔工具历史记录艺术画笔工具 历史记录画笔工具 历史记录画笔工具很简单&#xff0c;就是将画笔工具嗯&#xff0c;涂抹过的修改过的地方&#xff0c;然后用历史记录画笔工具重新修改回来&#xff0c;比如我们将三叠美元中的一叠用画笔工具先涂抹掉&#xf…...

编程日记 2023/10/14 9:48:19

Spark上使用pandas API快速入门

文章最前&#xff1a; 我是Octopus&#xff0c;这个名字来源于我的中文名--章鱼&#xff1b;我热爱编程、热爱算法、热爱开源。所有源码在我的个人github &#xff1b;这博客是记录我学习的点点滴滴&#xff0c;如果您对 Python、Java、AI、算法有兴趣&#xff0c;可以关注我的…...

编程日记 2023/10/14 9:47:17

【WebRTC---源码篇】（十：零）WEBRTC/StreamStatisticianImpl持续更新中)

StreamStatisticianImpl是WebRTC的一个内部实现类&#xff0c;用于统计和管理媒体流的各种统计信息。 StreamStatisticianImpl负责记录和计算以下统计数据&#xff1a; 1. 带宽统计&#xff1a;记录媒体流的发送和接收带宽信息&#xff0c;包括发送比特率、接收比特率、发送丢…...

编程日记 2023/10/14 9:46:15

​调用Lua脚本tostring(xxx)报attempt to call a nil value (global ‘tostring‘

在c程序里调用Lua脚本, 脚本中用到了转字符串 tostring(xxx) str "test" function output(a,b,c)d "a:"..tostring(a).."b:"..tostring(b).."c"..tostring(c)return d end 实际运行会报错&#xff1a; attempt to call a nil v…...

编程日记 2023/10/14 9:45:14

PBA.客户需求分析 需求管理

一、客户需求分析 1 需求的三个层次: Requirement/Wants/Pains 大部分人认为&#xff0c;产品满足不了客户需要&#xff0c;是因为客户告知的需求是错误的&#xff0c;这听起来有一些道理&#xff0c;却没有任何意义。不同角色对于需求的理解是不一样的。在客户的需求和厂家的…...

编程日记 2023/10/14 9:44:13

Kafka进阶

Kafka进阶 Kafka事务 kafka的事务机制是指kafka支持跨多个主题和分区的原子性写入&#xff0c;即在一个事务中发送的所有消息要么全部成功&#xff0c;要么全部失败。 kafka的事务机制涉及到以下几个方面&#xff1a; 事务生产者&#xff08;transactional producer&#x…...

编程日记 2023/10/14 9:43:13

大数计算：e^1000/300！

1.问题&#xff1a;大数计算可能超出数据类型范围 当单独计算 &#xff0c;因为 &#xff0c;double的最大取值为1.79769e308&#xff0c;所以 肯定超过了double的表示范围。 同样&#xff0c;对于300&#xff01;也是如此。 那我们应该怎么去计算和存储结果呢&#xff1f;…...

编程日记 2023/10/14 9:42:10

力扣164最大间距

1.前言 因为昨天写了一个基数排序&#xff0c;今天我来写一道用基数排序实现的题解&#xff0c;希望可以帮助你理解基数排序。 这个题本身不难&#xff0c;就是线性时间和线性额外空间(O(n))的算法&#xff0c;有点难实现 基数排序的时间复杂度是O(d*(nradix))&#xff0c;其中…...

编程日记 2023/10/14 9:41:09

聚观早报 | “百度世界2023”即将举办；2024款岚图梦想家上市

【聚观365】10月13日消息 “百度世界2023”即将举办 2024款岚图梦想家上市 腾势D9用户超10万 华为发布新一代GigaGreen Radio OpenAI拟进行重大更新 “百度世界2023”即将举办 “百度世界2023”将于10月17日在北京首钢园举办。届时&#xff0c;百度创始人、董事长兼首席执…...

编程日记 2023/10/14 9:39:07

Windows 应用程序监控重启

执行思路 1.定时关闭可执行程序&#xff0c;2.再通过定时监控启动可执行程序 定时启动关闭程序.bat echo off cd "D:\xxxx\" :: 可执行程序目录 Start "" /b xxxx.exe :: 可执行程序 timeout /T 600 /nobreak >nul :: 600秒 taskkill /IM xxxx.exe /…...

编程日记 2023/10/14 9:38:06