排序算法-快速排序法(QuickSort)
排序算法-快速排序法(QuickSort)
1、说明
快速排序法是由C.A.R.Hoare提出来的。快速排序法又称分割交换排序法,是目前公认的最佳排序法,也是使用分而治之(Divide and Conquer)的方式,会先在数据中找到一个虚拟的中间值,并按此中间值将所有打算排序的数据分为两部分。其中小于中间值的数据放在左边,而大于中间值的数据放在右边,再以同样的方式分别处理左右两边的数据,直到排序完为止。操作与分割步骤如下:
假设有n项记录,其键值为
。
- 先假设K的值为第一个键值。
- 从左向右找出键值
,使得
。
- 从左向右找出键值
,使得
。
- 如果
,那么
与
互换,并回到步骤2。
- 如果
,那么将
与
互相,并以
为基准点分割成左、右两部分,然后针对左、右两边执行步骤1~5,直到左边键值等于右边键值为止。
2、算法分析
- 在最好情况和平均情况下,时间复杂度为
。在最坏情况下就是每次挑中的中间值不是最大就是最小的,其时间复杂度为
。
- 快速排序法不是稳定排序法。
- 在最坏情况下,空间复杂度为
,而在最好情况下,空间复杂度为
。
- 快速排序法是平均运行时间最快的排序法。
3、C++代码
#include<iostream>
using namespace std;void Print(int tempData[], int tempSize) {for (int i = 0; i < tempSize; i++) {cout << tempData[i] << " ";}cout << endl;
}void Quick(int tempData[], int tempLeft, int tempRight) {int temp;int leftIndex;int rightIndex;int t;if (tempLeft < tempRight) {leftIndex = tempLeft + 1;rightIndex = tempRight;while (true) {for (int i = tempLeft + 1; i < tempRight; i++) {if (tempData[i] >= tempData[tempLeft]) {leftIndex = i;break;}leftIndex++;}for (int j = tempRight; j > tempLeft + 1; j--) {if (tempData[j] <= tempData[tempLeft]) {rightIndex = j;break;}rightIndex--;}if (leftIndex < rightIndex) {temp = tempData[leftIndex];tempData[leftIndex] = tempData[rightIndex];tempData[rightIndex] = temp;}else {break;}}if (leftIndex >= rightIndex) {temp = tempData[tempLeft];tempData[tempLeft] = tempData[rightIndex];tempData[rightIndex] = temp;Quick(tempData, tempLeft, rightIndex - 1);Quick(tempData, rightIndex + 1, tempRight);}}
}int main() {const int size = 10;int data[100] = { 32,5,24,55,40,81,17,48,25,71 };//32 5 24 55 40 81 17 48 25 71//32 5 24 25 40 81 17 48 55 71//32 5 24 25 17 81 40 48 55 71//17 5 24 25 32 81 40 48 55 71//5 17 24 25 32 81 40 48 55 71//5 17 25 24 32 81 40 48 55 71//5 17 25 24 32 71 40 48 55 81//5 17 25 24 32 55 40 48 71 81//5 17 25 24 32 48 40 55 71 81//5 17 25 24 32 40 48 55 71 81Print(data, size);Quick(data, 0, size - 1);Print(data, size);return 0;
}输出结果

相关文章:

排序算法-快速排序法(QuickSort)
排序算法-快速排序法(QuickSort) 1、说明 快速排序法是由C.A.R.Hoare提出来的。快速排序法又称分割交换排序法,是目前公认的最佳排序法,也是使用分而治之(Divide and Conquer)的方式,会先在数…...
Python 简介
一、Python 简介 Python 是著名的“龟叔” Guido van Rossum 在 1989 年圣诞节期间,为了打发无聊的圣诞节而编写的一个编程语言。牛人就是牛人,为了打发无聊时间竟然写了一个这么牛皮的编程语言。 现在,全世界差不多有 600 多种编程语言&am…...
grafana api创建dashboard 记录
文章目录 json model导入申请api key创建dashboard删除dashboard json model导入 直接在ui通过json model 导入,开发自己用还好,但对非开发人员不太友好,故考虑通过api后台自动创建 api doc : https://grafana.com/docs/grafana/v9.3/devel…...

局域网上IP多播与IP单播关于MAC地址的区别
IP单播进行到局域网上的时候: 网际层使用IP地址进行寻址,各路由器收到IP数据报后,根据其首部中的目的IP地址的网络号部分,基于路由表进行查表转发。 查表转发的结果可指明IP数据报的下一跳路由器的IP地址,但无法指明…...

三数之和[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个整数数组nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i ! j、i ! k且j ! k,同时还满足nums[i] nums[j] nums[k] 0。请你返回所有和为0且不重复的三元组。 注意:答案中不可以…...

基于天牛须优化的BP神经网络(分类应用) - 附代码
基于天牛须优化的BP神经网络(分类应用) - 附代码 文章目录 基于天牛须优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.天牛须优化BP神经网络3.1 BP神经网络参数设置3.2 天牛须算法应用 4.测试结果&#x…...

渗透波菜网站
免责声明 本文发布的工具和脚本,仅用作测试和学习研究,禁止用于商业用途,不能保证其合法性,准确性,完整性和有效性,请根据情况自行判断。如果任何单位或个人认为该项目的脚本可能涉嫌侵犯其权利,…...

Spring Boot:Dao层-实例介绍
目录 Dao层的作用Dao层的特点与 Service 层和 Controller 层的关系实例介绍MenuDaoOperatorLogDaoRoleDaoUserDao四个文件的共同点引用的包使用Repository注解继承JpaRepository接口接口的实体类的主键类型使用 Query()注解 Dao层的作用 负责与数据库进行交互,主要…...

接口测试入门:深入理解接口测试!
很多人会谈论接口测试。到底什么是接口测试?如何进行接口测试?这篇文章会帮到你。 一、前端和后端 在谈论接口测试之前,让我们先明确前端和后端这两个概念。 前端是我们在网页或移动应用程序中看到的页面,它由 HTML 和 CSS 编写…...
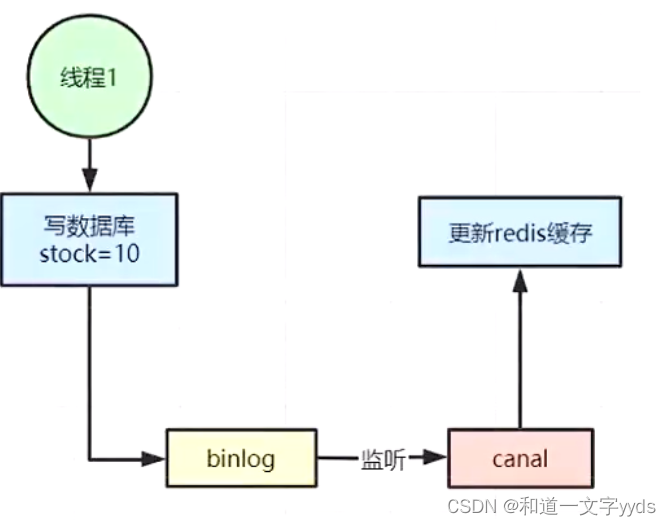
Redis微服务架构
Redis微服务架构 缓存设计 缓存穿透 缓存穿透是指查询一个根本不存在的数据,缓存层和存储层都不会命中,通常出于容错的考虑,如果从存储层查不到数据则不写入缓层。 缓存穿透将导致不存在的数据每次请求都要到存储层去查询,失去…...

【C++】 局部对象,引用返回
1、new 关键字 会在堆内申请空间,如果仅仅是普通调用构造函数,不会在堆内开辟空间。 2、函数调用会形成栈帧,进行压栈操作,函数调用结束,会进行弹栈。 函数内的局部对象,会随着弹栈,而被销毁(…...

线性代数中涉及到的matlab命令-第二章:矩阵及其运算
目录 1,矩阵定义 2,矩阵的运算 3,方阵的行列式和伴随矩阵 4,矩阵的逆 5,克莱默法则 6,矩阵分块 1,矩阵定义 矩阵与行列式的区别: (1)形式上行列式…...

计算机毕业设计选什么题目好?springboot 美食推荐系统
✍✍计算机编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java实战 |…...
爆肝整理,Jmeter接口性能测试-跨线程调用变量实操(超详细)
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、Jmeter中线程运…...
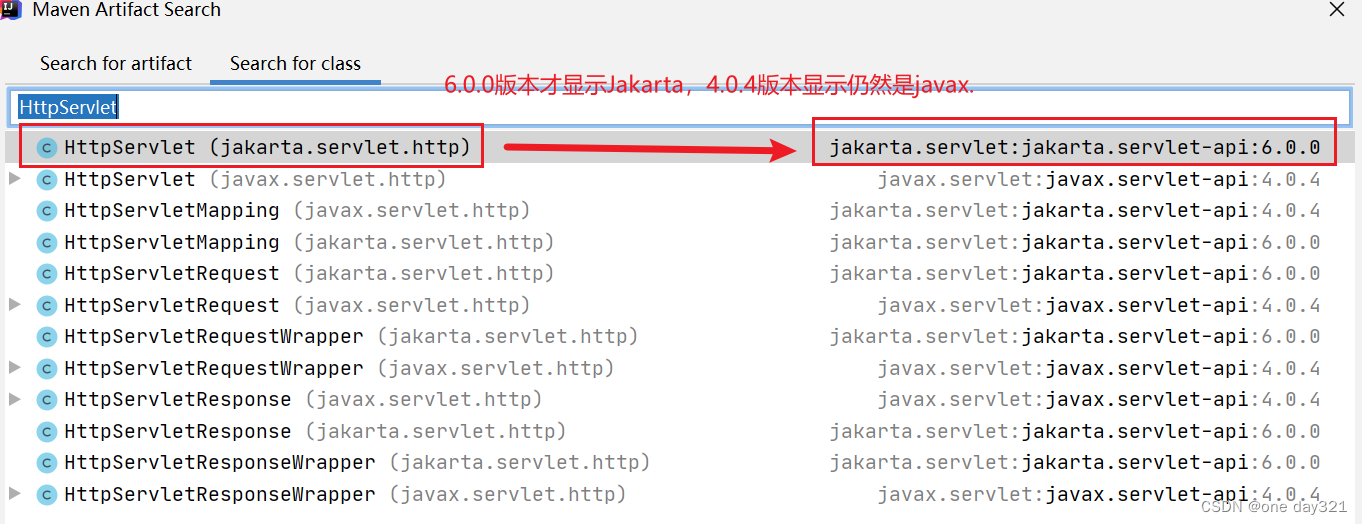
Maven导入程序包jakarta.servlet,但显示不存在
使用前提:(Tomcat10版本)已知tomcat10版本之后,使用jakart.servlet。而tomcat9以及之前使用javax.servlet。 问题描述:在maven仓库有导入了Jakarta程序包,但是界面仍然显示是javax。(下图&…...
es6(二)——常用es6说明
ES6的系列文章目录 es6(一)——var和let和const的区别 文章目录 ES6的系列文章目录一、变量的结构赋值1.数组的结构赋值2.对象的结构赋值 二、模板字符串三、扩展运算符1.字符串的使用2.数组的使用 四、箭头函数1.普通函数的定义2.箭头函数的定义3.箭头…...
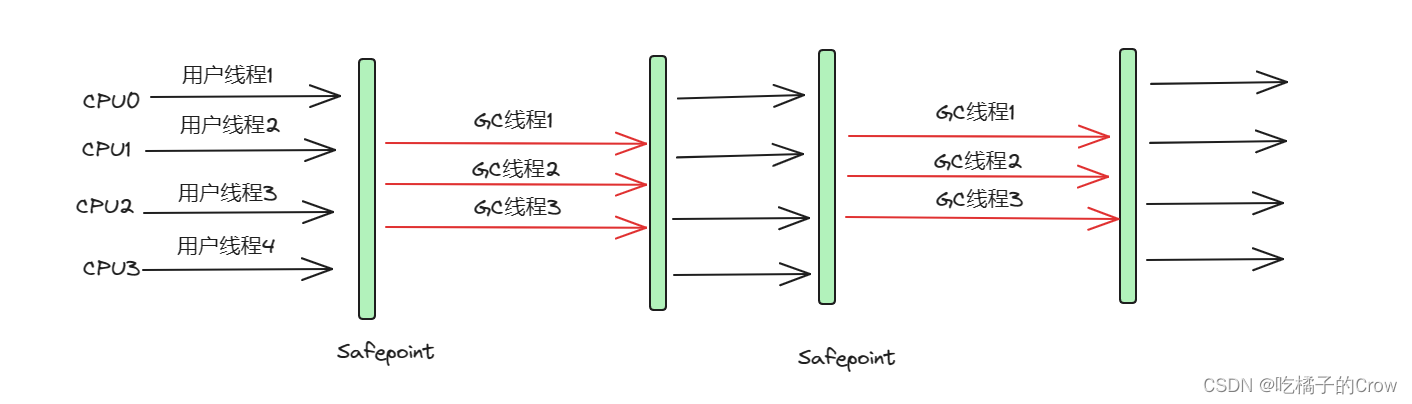
经典垃圾回收器
1.各垃圾回收器之间的配合使用关系 2.垃圾回收器的种类 2.1 Serial收集器(默认新生代收集器) Serial收集器是历史最悠久的收集器,曾经是新生代收集器的唯一选择,它是一个单线程工作的收集器,其“单线程”的意义不仅仅…...

台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法
台达DOP-B07S410触摸屏出现HMI no response无法上传的解决办法 台达触摸屏(B07S410)在上载程序时(显示No response from HMI)我以前的电脑是WIN7的,从来没出现过这样的问题,现在换成win10的,怎么都不行,(USB显示是一个大容量存储)换一台电脑(win10)有些行,有些不行…...

[资源推荐] 复旦大学张奇老师科研分享
刷B站的时候首页给我推了这个:【直播回放】复旦大学张奇教授亲授:人工智能领域顶会论文的发表指南先前也散漫地读了些许论文,但没有在一些宏观的方法论下去训练,读的时候能感觉出一些科研的套路,论文写作的套路&#x…...

C++数位动态规划算法:统计整数数目
题目 给你两个数字字符串 num1 和 num2 ,以及两个整数 max_sum 和 min_sum 。如果一个整数 x 满足以下条件,我们称它是一个好整数: num1 < x < num2 min_sum < digit_sum(x) < max_sum. 请你返回好整数的数目。答案可能很大&…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
