P1433 吃奶酪
#include <iostream>
#include <cmath>
using namespace std;
#define M 15
#define S(n) ((n) * (n))
double indx[M + 5], indy[M + 5], ans = 0, sum = 0;//坐标数组,从下标为1开始记录
int n, vis[M + 5] = { 0 };//vis数组,选过的数字标记为1,没选过的数字标记为0
double dis(int i, int j) {return sqrt(S(indx[i] - indx[j]) + S(indy[i] - indy[j]));
}
//c表示当前已经选了c个数字
//k表示最后一次选的是第k个点
void fun(int c, int k) {if (c == n) {if (!ans || ans > sum) ans = sum;return;}for (int i = 1; i <= n; i++) {if (vis[i]) continue;vis[i] = 1;sum += dis(i, k);fun(c + 1, i);vis[i] = 0;sum -= dis(i, k);}return;
}
int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> indx[i] >> indy[i];}fun(0, 0);printf("%.2lf", ans);return 0;
}8组超时,优化

#include <iostream>
#include <cmath>
using namespace std;
#define M 15
#define S(n) ((n) * (n))
double indx[M + 5], indy[M + 5], dp[70000][M + 5] = { 0 }, ans = 0; //坐标数组,从下标为1开始记录
//dp[i][j]:选择内容为i,最后一次选择的数字为j,的路径总长度
int n, vis[M + 5] = { 0 }; //vis数组,选过的数字标记为1,没选过的数字标记为0
double dis(int i, int j) { //返回第i个点到第j个点的距离return sqrt(S(indx[i] - indx[j]) + S(indy[i] - indy[j]));
}
//c表示当前已经选了c个数字
//k表示最后一次选的是第k个点
//m的二进制代表选择的内容
//sum表示这c个数字当前方案的路径总长度
void fun(int c, int k, int m, double sum) {if (c == n) {ans = sum;return;}dp[m][k] = sum; //到达一个新的节点,第一步就更新以m为内容,k为末端的路径长度for (int i = 1; i <= n; i++) {if (vis[i]) continue;int a = m + pow(2, i); //m如果自增,递归回来又要减,太麻烦,定义一个adouble d = dis(i, k); //后面最多用到三次,算出来方便用//以a为内容、i为路径已经被遍历过了,且之前的值小于等于这次遍历过去的值,那就不遍历过去了if (dp[a][i] != 0 && dp[a][i] <= sum + d) continue;//ans不为0且这次遍历过去sum超过ans,那就没必要过去了if (ans && ans <= sum + d) continue;vis[i] = 1;fun(c + 1, i, a, sum + d);vis[i] = 0;}return;
}
int main() {cin >> n;for (int i = 1; i <= n; i++) {cin >> indx[i] >> indy[i];}fun(0, 0, 0, 0);printf("%.2lf", ans);return 0;
}
相关文章:

P1433 吃奶酪
#include <iostream> #include <cmath> using namespace std; #define M 15 #define S(n) ((n) * (n)) double indx[M 5], indy[M 5], ans 0, sum 0;//坐标数组,从下标为1开始记录 int n, vis[M 5] { 0 };//vis数组,选过的数字标记为1…...
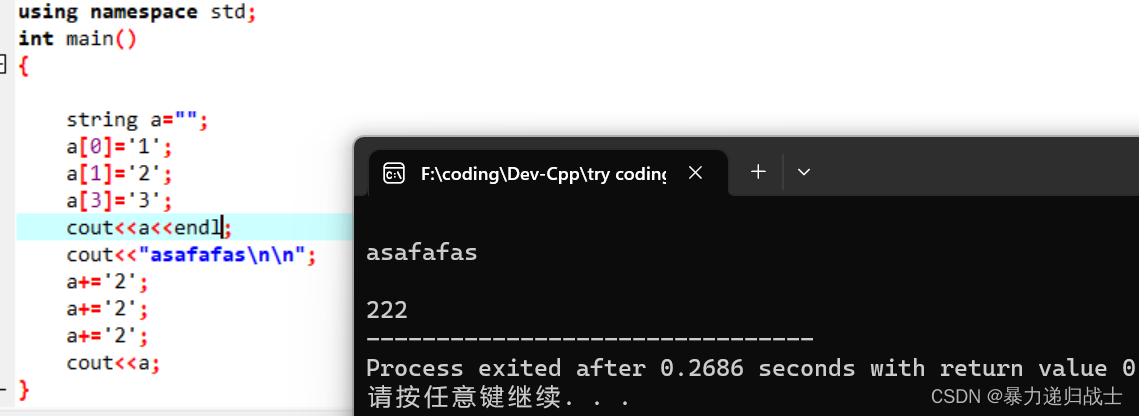
c++string类的赋值问题
来看问题: 为什么呢?是因为定义string a""时候a没有占用空间,所以没有a[0],a[1],a[3]。如果说string a"hhhhhh",那么图中a[0],a[1],a[3]就有效了。正确的做法是用连接,或者是定义时写成string a(6…...

服务器中了mkp勒索病毒怎么办?mkp勒索病毒特点,解密数据恢复
Mkp勒索病毒是最近比较流行的勒索病毒,从10月份国庆节假期结束以来,云天数据恢复中心陆续收到很多企业的求助,企业的服务器被mkp勒索病毒攻击,导致企业的众多软件无法正常使用,像用友与金蝶软件都有遭受过mkp勒索病毒的…...

深入探析网络代理与网络安全
随着互联网的快速发展,网络安全问题日益突出,而网络代理技术正成为应对安全挑战的重要工具。本文将深入探讨Socks5代理、IP代理以及它们在网络安全、爬虫开发和HTTP协议中的关键作用,以期帮助读者更好地理解和应用这些技术。 1. Socks5代理&…...

如何开始使用 Kubernetes RBAC
基于角色的访问控制 (RBAC) 是一种用于定义用户帐户可以在 Kubernetes 集群中执行的操作的机制。启用 RBAC 可以降低与凭证盗窃和帐户接管相关的风险。向每个用户授予他们所需的最低权限集可以防止帐户拥有过多的特权。 大多数流行的 Kubernetes 发行版都从单个用户帐户开始,…...

8.简易无线通信
预备知识 Zigbee无线通信,需要高频的载波来提供发射效率,Zigbee模块之间要可以正常的收发,接收模块必须把接收频率设置和发射模块的载波频率一致。Zigbee有27个载波可以进行通信,载波叫做信道(无线通信的通道…...

渗透测试漏洞挖掘技巧
文章目录 一、使用.json进行敏感数据泄漏二、如何查找身份验证绕过漏洞三、在Drupal上找到隐藏的页面四、遗忘的数据库备份五、电子邮件地址payloads六、HTTP主机头:localhost七、通过篡改URI访问管理面板八、通过URL编码空格访问管理面板九、篡改URI绕过403十、Byp…...

Nginx - 反向代理与负载均衡
目录 一、Nginx 1.1、Nginx 下载 1.2、nginx 基础配置的认识 a)第一部分:全局块 b)第二部分:events 块 c)第三部分:http 块 http 块中 内嵌的 server 块 1.3、一些常用配置 1.3.1、location 匹配级…...
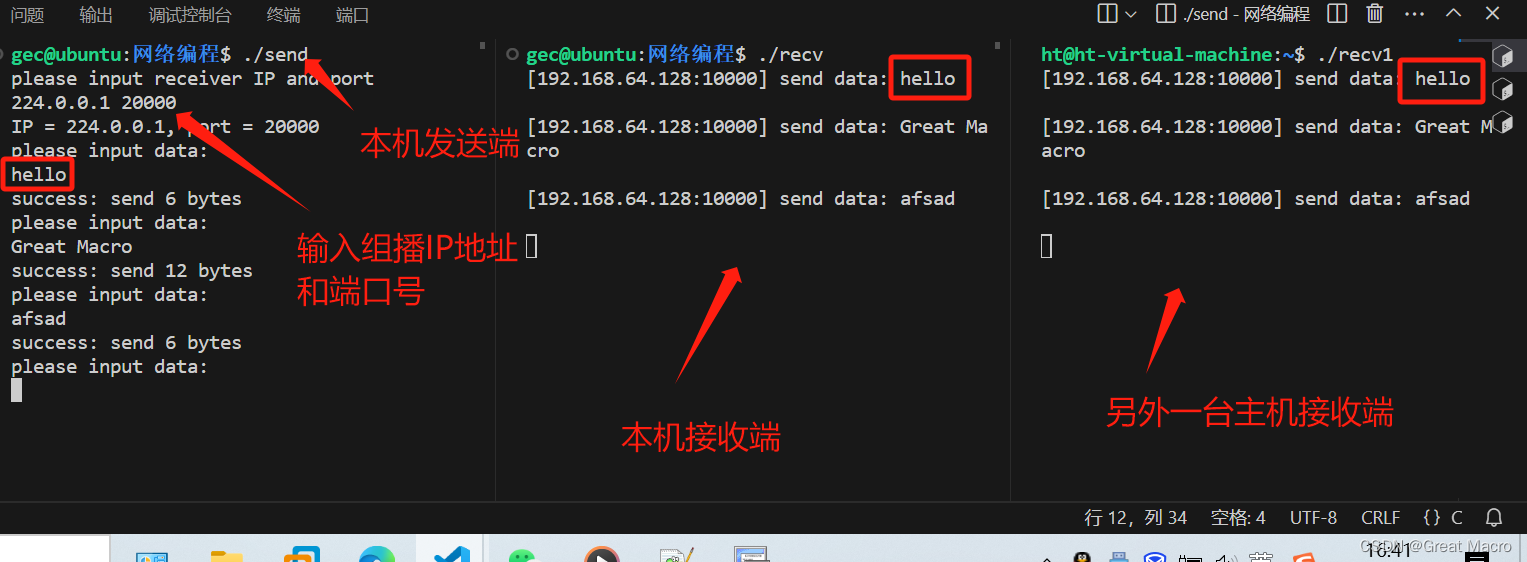
Linux网络编程系列之UDP组播
一、什么是UDP组播 UDP组播是指使用用户数据报协议(UDP)实现的组播方式。组播是一种数据传输方式,允许单一数据包同时传输到多个接收者。在UDP组播中,一个数据包可以被多个接收者同时接收,这样可以降低网络传输的负载和…...
-23)
设计模式~状态模式(state)-23
目录 (1)优点: (2)缺点: (3)使用场景: (4)注意事项: (5)应用实例: 代码 在状态模式(State Pattern)中,类的行为是基于它的状态改变的。这种类型的设计模式属于行为型模式。在状…...
linux环境下使用lighthouse与selenium
一、安装谷歌浏览器、谷歌浏览器驱动、lighthouse shell脚本 apt update && apt -y upgrade apt install -y curl curl -fsSL https://deb.nodesource.com/setup_18.x | bash apt install -y nodejs apt install -y npm npm install -g lighthouse apt-get install -y …...
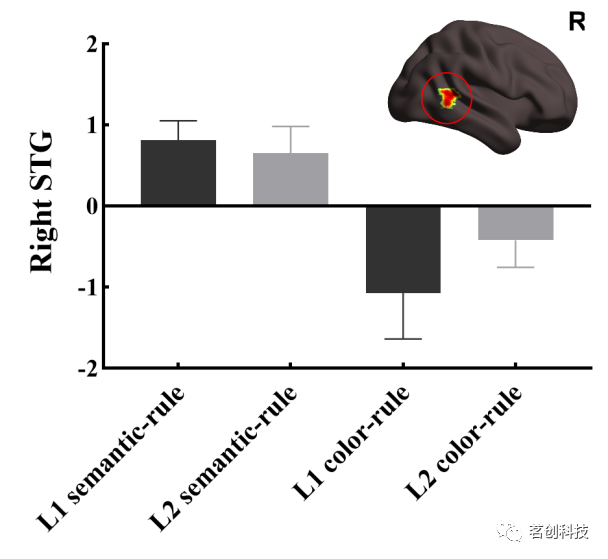
NeuroImage | 右侧颞上回在语义规则学习中的作用:来自强化学习模型的证据
在现实生活中,许多规则的获取通常需要使用语言作为桥梁,特别是语义在信息传递中起着至关重要的作用。另外,个体使用的语言往往具有明显的奖励和惩罚元素,如赞扬和批评。一种常见的规则是寻求更多的赞扬,同时避免批评。…...
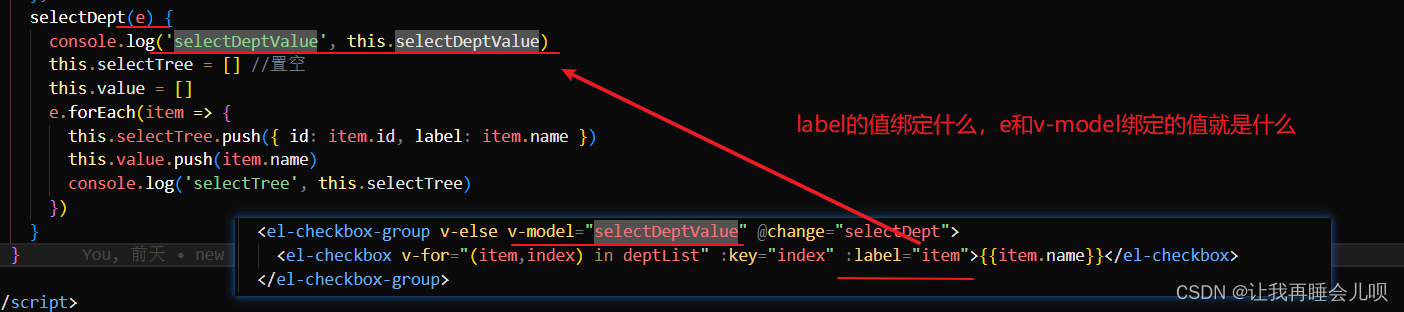
uni-app编程checkbox-group获取选中的每个checkbox的value值
uni-app编程checkbox-group获取选中的每个checkbox的value值_uniappcheckboxvalue-CSDN博客...

数组——螺旋矩阵II
文章目录 一、题目二、题解 题目顺序:代码随想录算法公开课,b站上有相应视频讲解 一、题目 59. Spiral Matrix II Given a positive integer n, generate an n x n matrix filled with elements from 1 to n2 in spiral order. Example 1: Input: n …...

反范式化设计
反范式化设计与范式化设计相对立。范式化设计是将数据组织成多个表,以最小化数据的冗余和提高数据一致性。相反,反范式化设计是故意增加冗余,以提高查询性能和降低复杂性。反范式化设计通常用于需要高度优化的读取密集型应用程序,…...

CCF CSP认证 历年题目自练Day31
题目一 试题编号: 202206-1 试题名称: 归一化处理 时间限制: 500ms 内存限制: 512.0MB 题目背景 在机器学习中,对数据进行归一化处理是一种常用的技术。 将数据从各种各样分布调整为平均值为 0、方差为 1的标准分布&a…...
)
PCL点云处理之从两片点云中获取具有匹配关系的同名点对 (二百一十八)
PCL点云处理之从两片点云中获取具有匹配关系的同名点对 (二百一十八) 一、算法介绍二、算法实现1.代码2.效果一、算法介绍 点云配准的前提是,我们知道或者预测了一些匹配对,我们认为这些匹配对就是两片点云中的同名点,同名点就是由于激光扫描存在误差的关系,导致同一地物…...
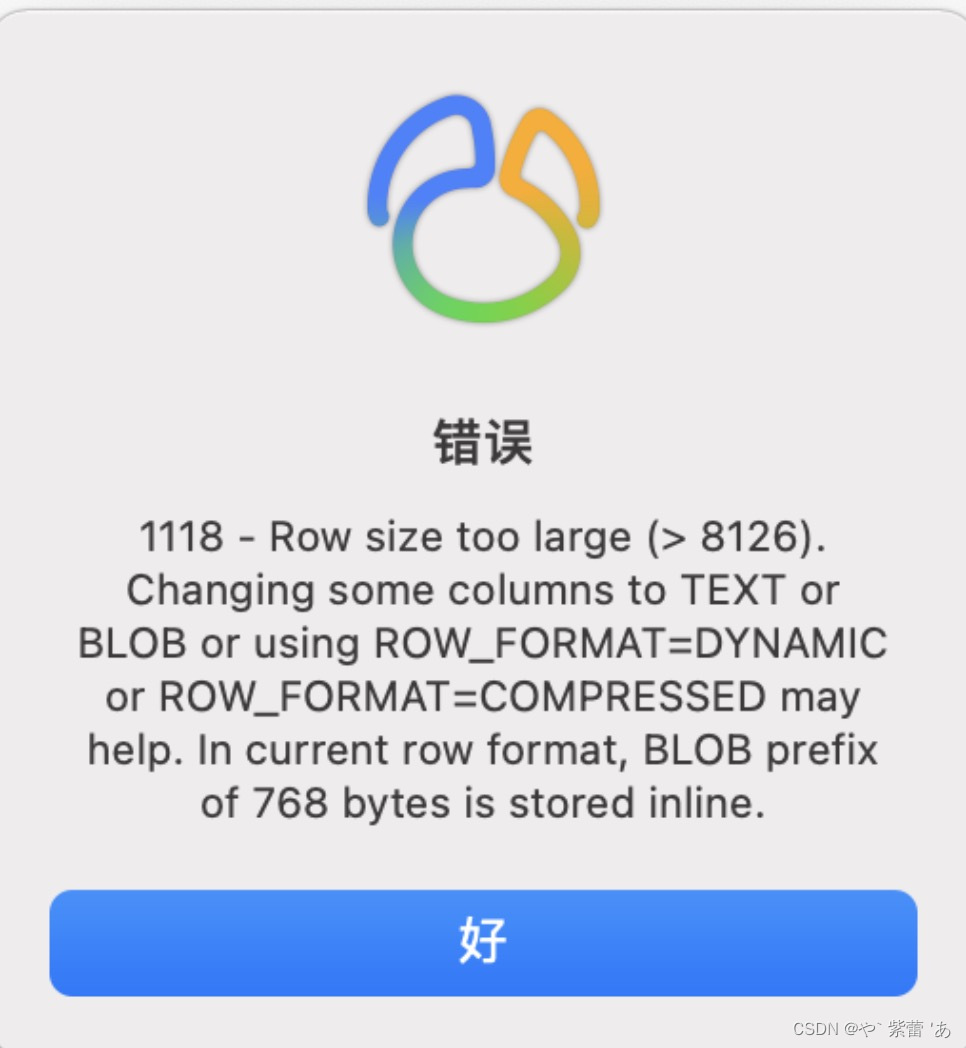
MySQL Row size too large (> 8126)
错误信息 ERROR 1118 (42000) at line 901: Row size too large (> 8126). Changing some columns to TEXT or BLOB or using ROW_FORMATDYNAMIC or ROW_FORMATCOMPRESSED may help. In current row format, BLOB prefix of 768 bytes is stored inline. 错误原因 这个问题…...
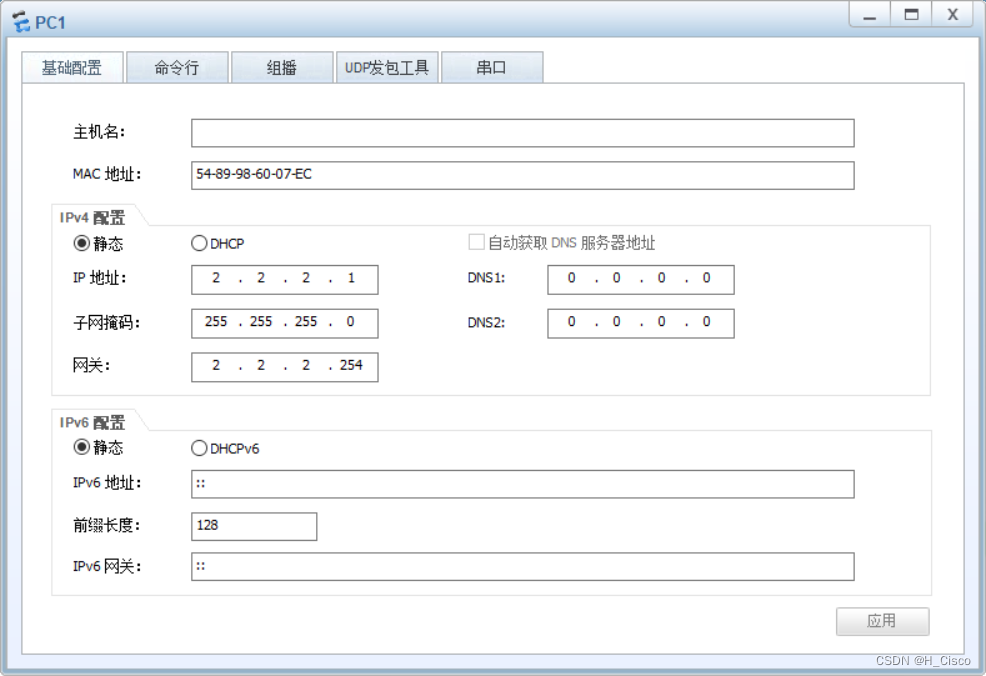
HUAWEI(26)——防火墙双机热备
一、拓扑 二、需求 PC2 ping PC1 FW1与FW2双机热备,FW1为active,FW2为Standby,抢占延时1s VRRP 三、配置 1.IP地址,防火墙接口加入区域 防火墙用户名:admin 防火墙旧密码:Admin@123 防火墙新密码:admin@123 [FW1]interface GigabitEthernet 1/0/0 [FW1-GigabitEthe…...

【ArcGIS】NDVI估算植被覆盖度FVC
NDVI估算植被覆盖度FVC NDVI计算植被覆盖度FVC计算NDVI估算植被覆盖度FVC操作步骤Step1:调出栅格计算器工具Step2:查找NDVIStep3: 参考 NDVI计算 植被覆盖度FVC计算 NDVI估算植被覆盖度FVC操作步骤 Step1:调出栅格计算器工具 1、首先打开软件&#x…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...
