AtCoder Beginner Contest 324(F)
AtCoder Beginner Contest 324
F Beautiful Path
需要一点思维的转化,一时竟然没想到。
题意
给定大小为 n n n 的有向图, m m m 条边,每条边有 b i , c i b_i,c_i bi,ci 两个属性,需要找到一条从 1 ∼ n 1\sim n 1∼n 的路径使得 w i = ( b 1 + b 2 + ⋯ + b k ) / ( c 1 + c 2 + ⋯ + c k ) w_i = (b_1+b_2+\dots+b_k) / (c_1+c_2+\dots+c_k) wi=(b1+b2+⋯+bk)/(c1+c2+⋯+ck) 最大。题目保证路径一定存在且无环。
思路
初看一时没思路,写了个到达 u u u 点时,以 w i w_i wi 的最大值为最优跑拓扑排序,这样显然是不对的,例如: 1 1 → 3 2 = 1 + 3 1 + 2 \frac 11\rightarrow \frac32 = \frac{1+3}{1+2} 11→23=1+21+3 会比 1 1 → 1 1 = 1 + 1 1 + 1 \frac11\rightarrow \frac11=\frac{1+1}{1+1} 11→11=1+11+1 更优,但是若是下一条边是 100 1 \frac{100}1 1100,两条路径更优的是 1 + 1 + 100 1 + 1 + 1 > 1 + 3 + 100 1 + 2 + 1 \frac{1+1+100}{1+1+1}>\frac{1+3+100}{1+2+1} 1+1+11+1+100>1+2+11+3+100.
这里需要转换一下思路:
求路径使得 max ( b 1 + b 2 + b 3 ) / ( c 1 + c 2 + c 3 ) = w i \max(b_1 + b_2 + b_3) / (c_1 + c_2 + c_3) = w_i max(b1+b2+b3)/(c1+c2+c3)=wi
设答案为 r e s res res
( b 1 + b 2 + b 3 ) / ( c 1 + c 2 + c 3 ) = r e s (b_1 + b_2 + b_3) / (c_1 + c_2 + c_3) = res (b1+b2+b3)/(c1+c2+c3)=res
( b 1 + b 2 + b 3 ) = ( c 1 + c 2 + c 3 ) ∗ r e s (b_1 + b_2 + b_3) = (c_1 + c_2 + c_3) * res (b1+b2+b3)=(c1+c2+c3)∗res
b 1 − c 1 ∗ r e s + b 2 − c 2 ∗ r e s + b 3 − c 3 ∗ r e s = 0 b_1 - c_1 * res + b_2 - c_2 * res + b_3 - c_3 * res = 0 b1−c1∗res+b2−c2∗res+b3−c3∗res=0
上式将 = = = 改成 ≥ \geq ≥ 显然也成立,于是就有了单调性,二分答案求解。
用拓扑排序时有个小坑点,从 1 1 1 出发可能有些节点到达不了,需要清除这些点的度。或者由于一定是小编号 → \rightarrow → 大编号,可以直接循环求解。
代码
#include <bits/stdc++.h>
using namespace std;#define ll long long
#define double long doubleconst int N = 2e5 + 10;struct node{int v, b, c;
};
vector<node> g[N];int n, m, d[N], t[N];
double f[N];
bool topu(double x){queue<int> q;for(int i = 1; i <= n; i ++){t[i] = d[i];f[i] = -1e10;}q.push(1);f[1] = 0.0;while(!q.empty()){int u = q.front(); q.pop();for(auto [v, b, c] : g[u]){f[v] = max(f[v], f[u] + (double)b - (double)c * x);t[v] --;if(!t[v]) q.push(v);}}return f[n] >= 0;
}int vis[N];
void dfs(int u){if(vis[u]) return ;vis[u] = 1;for(auto [v, a, b] : g[u]) dfs(v);
}int main(){ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);cin >> n >> m;for(int i = 1; i <= m; i ++){int u, v, b, c;cin >> u >> v >> b >> c;g[u].push_back({v, b, c});d[v] ++;}dfs(1);for(int i = 1; i <= n; i ++){ // 清除无法到达的节点的度if(vis[i]) continue ;for(auto [v, a, b] : g[i]) d[v] --;}double l = 0, r = 2e9;for(int i = 1; i <= 100; i ++){double mid = (l + r) / 2;if(topu(mid)) l = mid;else r = mid;}cout << fixed << setprecision(20) << l <<"\n";return 0;
}
G Generate Arrays(待补)
题意
思路
代码
相关文章:
)
AtCoder Beginner Contest 324(F)
AtCoder Beginner Contest 324 F Beautiful Path 需要一点思维的转化,一时竟然没想到。 题意 给定大小为 n n n 的有向图, m m m 条边,每条边有 b i , c i b_i,c_i bi,ci 两个属性,需要找到一条从 1 ∼ n 1\sim n 1∼n…...
-- i2s - 数字音频)
LuatOS-SOC接口文档(air780E)-- i2s - 数字音频
示例 -- 这个库属于底层适配库, 具体用法请查阅示例 -- demo/multimedia -- demo/tts -- demo/record常量 常量 类型 解释 i2s.MODE_I2S number I2S标准,比如ES7149 i2s.MODE_LSB number LSB格式 i2s.MODE_MSB number MSB格式,比如TM8211 …...

瑞芯微RK3568核心板在边缘服务器产品中的应用-迅为电子
迅为RK3568核心板在边缘服务器产品中可以发挥关键作用,为边缘计算应用提供高性能的计算和多媒体处理能力。边缘服务器通常用于处理和存储数据,执行本地计算任务,并支持与远程云服务的通信。以下是RK3568核心板在边缘服务器产品中的应用方案&a…...

pg ash自制版 pg_active_session_history
一、 实现功能 由于pgsentinel插件存在严重的内存占用问题,本篇改为自行实现,但其语句仍可以参考pgsentinel插件。PostgreSQL ash —— pgsentinel插件 学习与踩坑记录_CSDN博客 v1.0 根据pg 14版本设计及测试,仅支持收集主库信息。默认每10秒…...
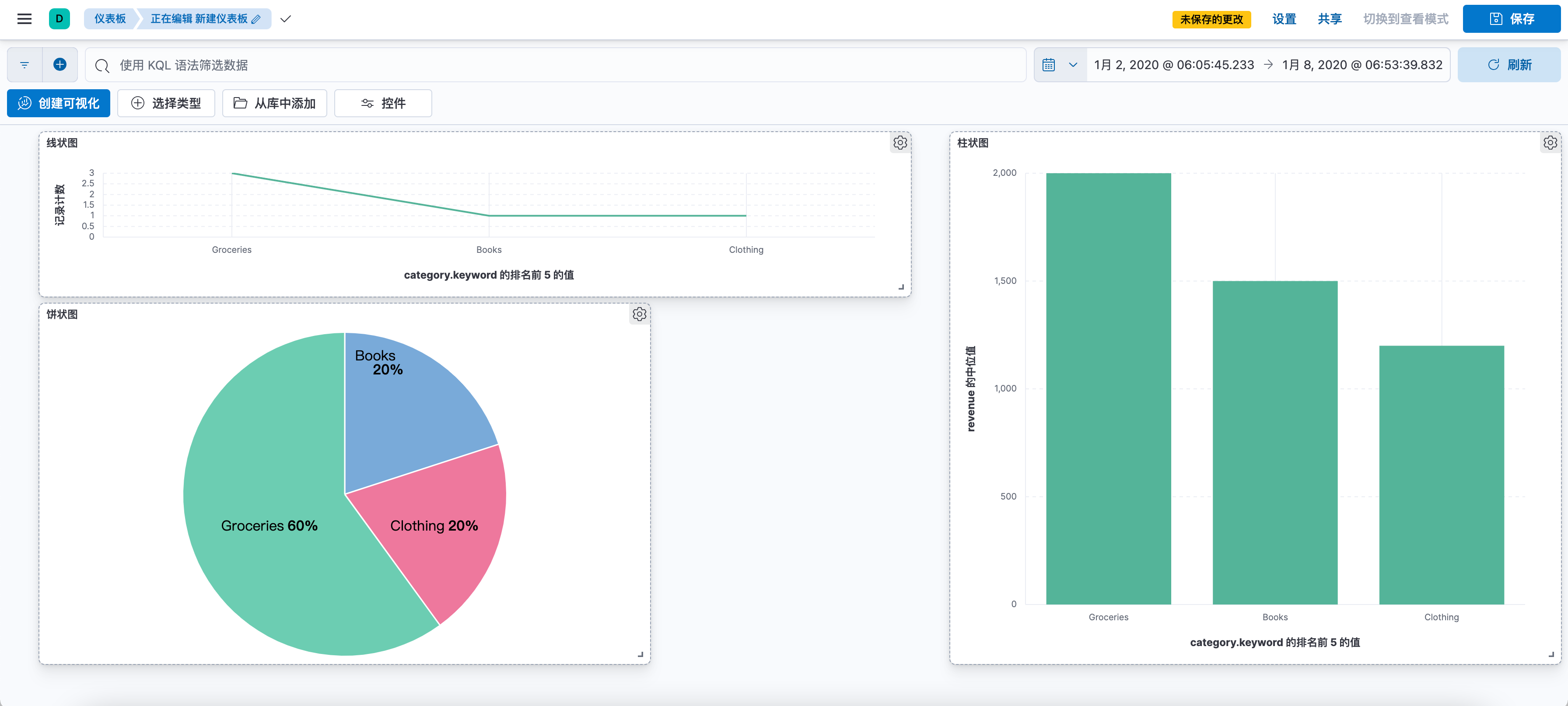
Elasticsearch系列组件:Kibana无缝集成的数据可视化和探索平台
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...
phpcms_v9模板制作及二次开发常用代码
0:调用最新文章,带所在版块 {pc:get sql"SELECT a.title, a.catid, b.catid, b.catname, a.url as turl ,b.url as curl,a.id FROM v9_news a, v9_category b WHERE a.catid b.catid ORDER BY a.id DESC " num"15" cache"300"} {lo…...
-概述)
自然语言处理(NLP)-概述
NLP 一、什么是自然语言处理(NLP)二、NLP的发展三、相关理论1 语言模型2 词向量表征和语义分析3 深度学习 一、什么是自然语言处理(NLP) 什么是自然语言处理 二、NLP的发展 三、相关理论 1 语言模型 序列数据形式多样…...

Python开发者的宝典:CSV和JSON数据处理技巧大公开!
更多资料获取 📚 个人网站:涛哥聊Python 在Python中处理CSV和JSON数据时,需要深入了解这两种数据格式的读取、写入、处理和转换方法。 下面将详细介绍如何在Python中处理CSV和JSON数据,并提供一些示例和最佳实践。 CSV数据处理…...

Unity中Commpont类获取子物体的示例
// 本脚本用于演示Component类 方法 //任何一个组件 都可以从游戏物体获取或者从其父对象哪里 子对象哪里获取,一个组件也可以拿到同一个物体上的其他组件 using System.Collections; using System.Collections.Generic; using UnityEngine; public class Component…...
【Vue面试题二十一】、Vue中的过滤器了解吗?过滤器的应用场景有哪些?
文章底部有个人公众号:热爱技术的小郑。主要分享开发知识、学习资料、毕业设计指导等。有兴趣的可以关注一下。为何分享? 踩过的坑没必要让别人在再踩,自己复盘也能加深记忆。利己利人、所谓双赢。 面试官:Vue中的过滤器了解吗&am…...

Unity 3D基础——缓动效果
1.在场景中新建两个 Cube 立方体,在 Scene 视图中将两个 Cude的位置错开。 2.新建 C# 脚本 MoveToTarget.cs(写完记得保存) using System.Collections; using System.Collections.Generic; using UnityEngine;public class MoveToTarget : M…...

高校教务系统登录页面JS分析——南京邮电大学
高校教务系统密码加密逻辑及JS逆向 本文将介绍南京邮电大学教务系统的密码加密逻辑以及使用JavaScript进行逆向分析的过程。通过本文,你将了解到密码加密的基本概念、常用加密算法以及如何通过逆向分析来破解密码。 本文仅供交流学习,勿用于非法用途。 一…...
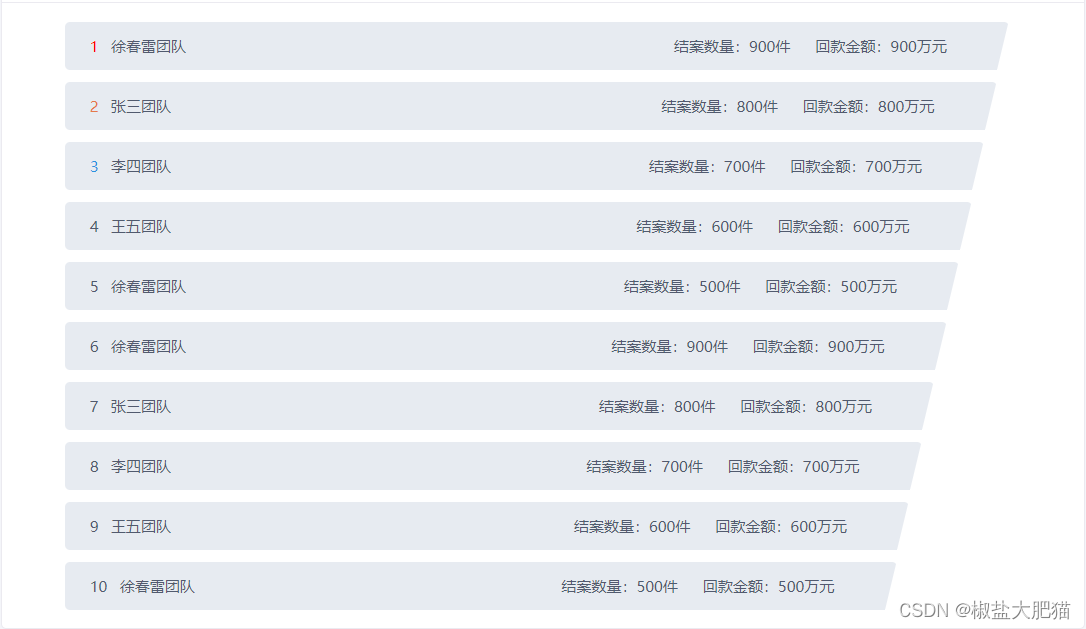
css实现排行榜样式(vue组件)
先看效果图: <template><div class"lawyer-refund-wrap"><div class"content"><divv-for"(item, index) in dataList" :key"index":style"{width: calc(100% - ${(index 1) * 10}px)}"c…...

I2VGen-XL高清图像生成视频大模型
本项目I2VGen-XL旨在解决根据输入图像生成高清视频任务。I2VGen-XL由达摩院研发的高清视频生成基础模型之一,其核心部分包含两个阶段,分别解决语义一致性和清晰度的问题,参数量共计约37亿,模型经过在大规模视频和图像数据混合预训…...
-每天10个小知识)
Angular知识点系列(1)-每天10个小知识
目录 1. Angular工作原理和与其他前端框架的区别2. 使用Angular的经验和最喜欢的特性3. 使用的最复杂的Angular组件或指令4. Angular的依赖注入系统和示例5. Angular的模块和组件生命周期6. 使用Angular路由和路由保护7. 在Angular应用中实现延迟加载8. 处理Angular应用中的状态…...
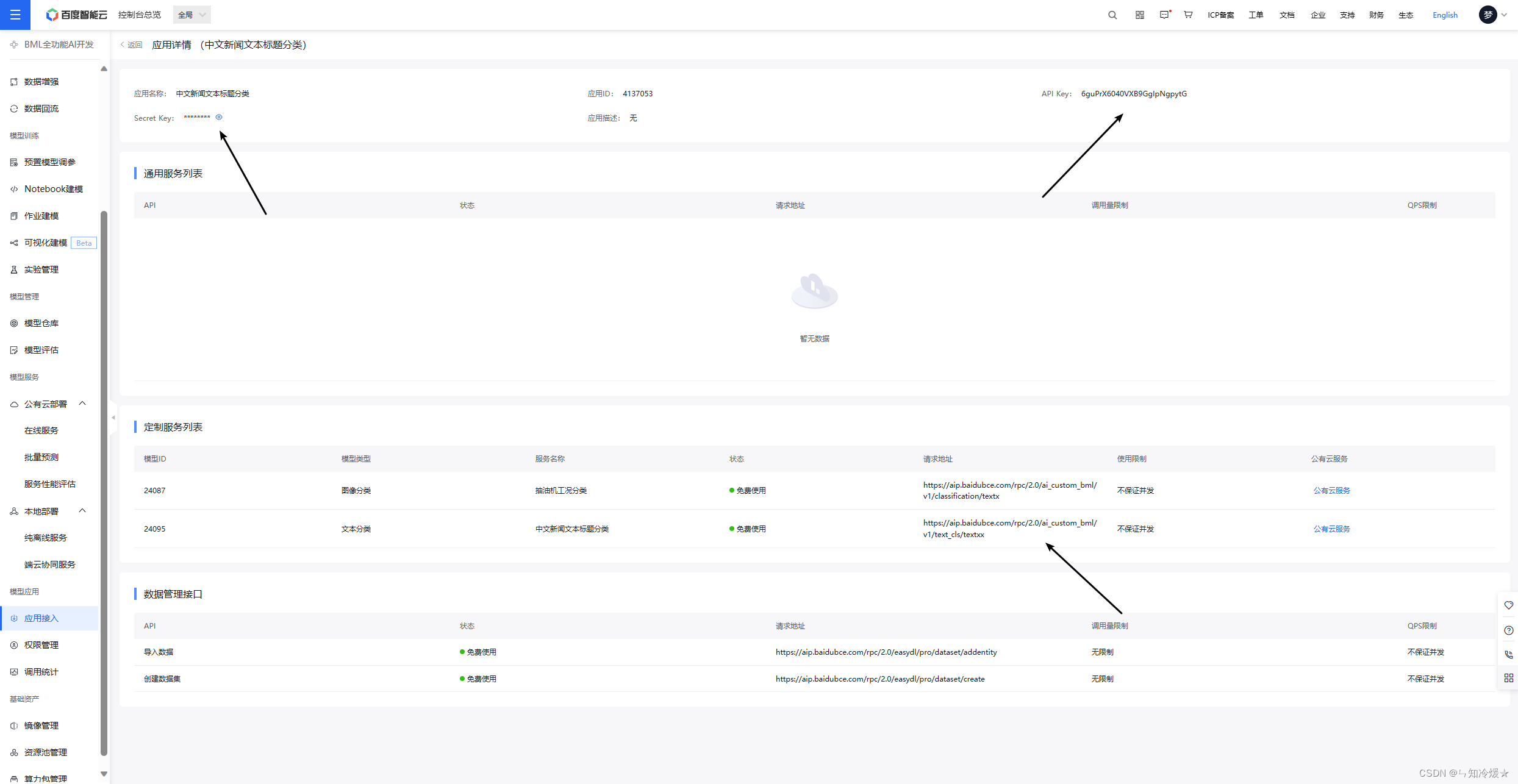
【从0开发】百度BML全功能AI开发平台【实操:以部署情感分析模型为例】
目录 一、全功能AI开发平台介绍二、AI项目落地应用流程(以文本分类为例)2-0、项目开始2-1、项目背景2-2、数据准备介绍2-3、项目数据2-4、建模调参介绍2-5、项目的建模调参2-6、开发部署2-7、项目在公有云的部署 附录:调用api代码总结 一、全…...

源码解析FlinkKafkaConsumer支持punctuated水位线发送
背景 FlinkKafkaConsumer支持当收到某个kafka分区中的某条记录时发送水位线,比如这条特殊的记录代表一个完整记录的结束等,本文就来解析下发送punctuated水位线的源码 punctuated 水位线发送源码解析 1.首先KafkaFetcher中的runFetchLoop方法 public…...
--- 父子组件传值)
vue3学习(五)--- 父子组件传值
文章目录 defineProps普通写法TS写法 defineEmits普通写法TS写法 defineExpose defineProps 和 defineEmits 都是只能在 <script setup> 中使用的编译器宏。他们不需要导入,且会随着 <script setup> 的处理过程一同被编译掉。 defineProps 接收父组件传…...

寻找AI时代的关键拼图,从美国橡树岭国家实验室读懂AI存力信标
超算,是计算产业的明珠,是人类探索未知的航船。超算的发展与变化,不仅代表着各个国家与地区间的科技竞争力,更将作为趋势风向标,影响整个数字化体系的走向。 在目前阶段,超算与AI计算的融合是大势所趋。为了…...

多线程并发篇---第十二篇
系列文章目录 文章目录 系列文章目录一、说说ThreadLocal原理?二、线程池原理知道吗?以及核心参数三、线程池的拒绝策略有哪些?一、说说ThreadLocal原理? hreadLocal可以理解为线程本地变量,他会在每个线程都创建一个副本,那么在线程之间访问内部 副本变量就行了,做到了…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
