九方财富冲刺上市:付费用户开始减少,退款金额飙升至4.9亿元
日前,九方财富控股有限公司(下称“九方财富”)通过港交所上市聆讯,并披露了聆讯后招股书。据贝多财经了解,九方财富最早于2021年8月31日在港交所递表,后在2022年3月、9月分别进行了更新。
据每日经济新闻报道,九方财富将于2月28日进入招股阶段。这意味着,九方财富有望将于2023年3月份正式登陆港交所。据报道,九方财富旗下主要子公司上海九方云智能科技有限公司(简称“上海九方云”)1996年成立,1998年取得证券投资顾问资质。

据招股书介绍,九方财富控股是一家在线投资决策解决方案提供商,提供在线投资者内容服务,包括在线高端投教服务及在线财商教育服务以及金融信息软件服务,帮助个人投资者更好地了解金融市场及制定投资计划或决策。
根据弗若斯特沙利文的资料,按2021年20.01亿元的总订单额及5.9%的市场份额计算,九方财富是我国第二大在线投资决策解决方案提供商。同时,该公司2021年在线高端投教服务及在线财商教育服务的总订单金额为13.91亿元,对应市场份额为11.2%。
贝多财经查询九方财富招股书发现,该公司的营收整体保持增长态势,但增长速率已经明显放缓,尤其是在2022年前10个月,同比增长速度减少至43.5%,相较于2019年至2021年的复合增长率104.72%下降约60个百分点,不过仍处于较高水平。
另一方面,九方财富产生的退款金额持续飙升,尤其是2021年和2022年前10个月。对此,九方财富归因于“金融市场的波动”。此外,九方财富的在线高端投教服务付费用户数量也在减少。
收入保持增长,增速有所放缓
据贝多财经了解,九方财富的经营主体包括上海富动文化传媒有限公司、上海九方云等,主要产品包括九方智投、赢马学堂、九方擒龙等,分别提供在线高端投教服务、在线财商教育服务以及在线金融信息软件服务等。
根据天眼查信息,上海九方云的前称为上海新汇通投资顾问有限公司,成立1996年8月,法定代表人为才子,全资股东为上海富动文化传媒有限公司。特别说明的是,上海九方云曾与其原股东对簿公堂。
据了解,福建华伦集团有限公司曾是上海九方云(即上海新汇通投资顾问有限公司)的股东。2018年7月、2019年11月,厦门市思明区人民法院曾分别对福建华伦集团有限公司持有的上海九方云0.5%、10%股权进行拍卖处理,评估价分别为7.47万元、31.40万元。
招股书显示,九方财富的收入整体保持增长态势。2019年、2020年、2021年和2022年前10个月,九方财富的收入分别约为2.74亿元、7.09亿元、11.49亿元和15.46亿元,净利润分别为-5784.0万元,8668.2万元、2.32亿元和3.48亿元。
贝多财经发现,九方财富的收入主要由在线高端投教服务、在线财商教育服务和金融信息软件服务三个板块构成。其中,在线高端投教服务收入的贡献比例最高,对应的收入占比分别为100.0%、100.0%、79.2%和61.7%。
据招股书介绍,九方财富于2021年起推出在线财商教育服务和金融信息软件服务。2021年和2022年前10个月,九方财富的金融信息软件服务收入分别为2.88亿元、5.89亿元,占总收入的比例分别为15.7%和38.2%,成为该公司新的增长点。
若剔除在线财商教育服务和金融信息软件服务收入,则九方财富的业绩增速则已经大幅放缓。2019年至2021年,九方财富的在线高端投教服务收入对应的复合年增长率高达104.72%,而2022年前10月则同比增长6.72%,降速明显。
纵观全局,九方财富的收入增速同样有所放缓。招股书显示,九方财富2019年的收入增长率为2726.7%,2020年、2021年度分别为158.4%和104.9%,而在2022年前10月则进一步下降至43.9%。
不过,九方财富的毛利率仍处于较高水平。2019年、2020年、2021年度和2022年前10个月,九方财富的毛利率分别为82.5%、89.7%、86.7%和88.4%,对应的净利率分别为-21.1%、12.2%、16.0%和22.5%,盈利水平持续优化。
付费用户减少,退款金额飙升
贝多财经注意到,九方财富的在线高端投教服务付费用户已经开始减少。招股书显示,九方财富的在线高端投教服务付费用户在2022年前10个月为30698人,而2021年前10个月则为31564人,相对减少866人。
于2019年、2020年及2021年以及截至2021年及2022年10月31日止10个月,九方财富的退款率分别为9.8%、12.5%、16.1%、16.1%及25.2%。九方财富在招股书中称,由于金融市场的波动,其截至2022年10月31日止十个月的退款率较2021年同期有所上升。
九方财富认为,在市场低迷期间,尤其是当个人投资者遭受损失时,他们倾向于将投资结果归因于该公司产品的质量,或自然会避免进一步投资或相关活动(包括使用该公司的产品),这将导致其客户提出的退款请求数量增加。
2019年、2020年和2021年,九方财富的退款金额分别约为4500万元、1.46亿元和3.83亿元。2022年前10个月,九方财富的退款金额则约为5.09亿元,2021年同期约为2.84亿元,同比增加79.24%。
按业务类型来看,九方财富的金融信息软件服务业务退款金额的增长更为明显。整个2021年,该公司的金融信息软件服务业务退款金额约为1.14亿元,2022年前10个月则达到2.17亿元,占总退款金额的比重增至42.7%。
而按是否为活跃付费用户划分,活跃付费用户则“接棒”非活跃付费用户成为退款的主力军。其中,2019年非活跃付费用户的退款金额约为2670万元,占比为59.3%。而在2020年、2021年和2022年前10月,非活跃付费用户的退款占比均不足4%。
相比之下,九方财富的活跃付费用户在2019年的退款金额仅约为1830万元,而2020年则增至1.44亿元,2021年度进一步增加至3.71亿元。2022年前10个月,九方财富的活跃付费用户退款金额更是达到4.91亿元。
事实上,另外一个指标更为突出,尤其是2021年和2022年。2019年、2020年和2021年以及2022年前10个月,九方财富因“产品/服务未能令人满意”产生的退款金额分别约为2320万元、7500万元、1.84亿元和2.23亿元。
另外,由于公司持有证券投资顾问资质,九方财富须接受中国证监会的定期检查。于2019年4月,中国证监会上海证监局对该公司进行现场检查,并发出了一份公告函,指出该公司运营中的五个问题。
其中,包括:(i)风险披露声明及服务协议中缺乏披露及客户身份识别不充分,(ii)投资建议依据的来源披露不足,(iii)使用第三方账户不当收取证券投资顾问服务费,(iv)若干员工的误导性宣传,及(v)确保记录可追溯性措施不足。
相关文章:

九方财富冲刺上市:付费用户开始减少,退款金额飙升至4.9亿元
日前,九方财富控股有限公司(下称“九方财富”)通过港交所上市聆讯,并披露了聆讯后招股书。据贝多财经了解,九方财富最早于2021年8月31日在港交所递表,后在2022年3月、9月分别进行了更新。 据每日经济新闻报…...
SSM+HTML搭建(小白教学)
最近做项目,觉得还是有意义记录以下前后端框架是怎么搭建的,今天给大家介绍介绍SSM:SpringBootSpringMVCMyBatis后端搭建:SpringBoot快速搭建的网站(Spring Initializr)选择创建之后,会下载到一个zip压缩包,对压缩包进行解压(包地址一般选择后端项目的放的文件夹中)用idea打开项…...
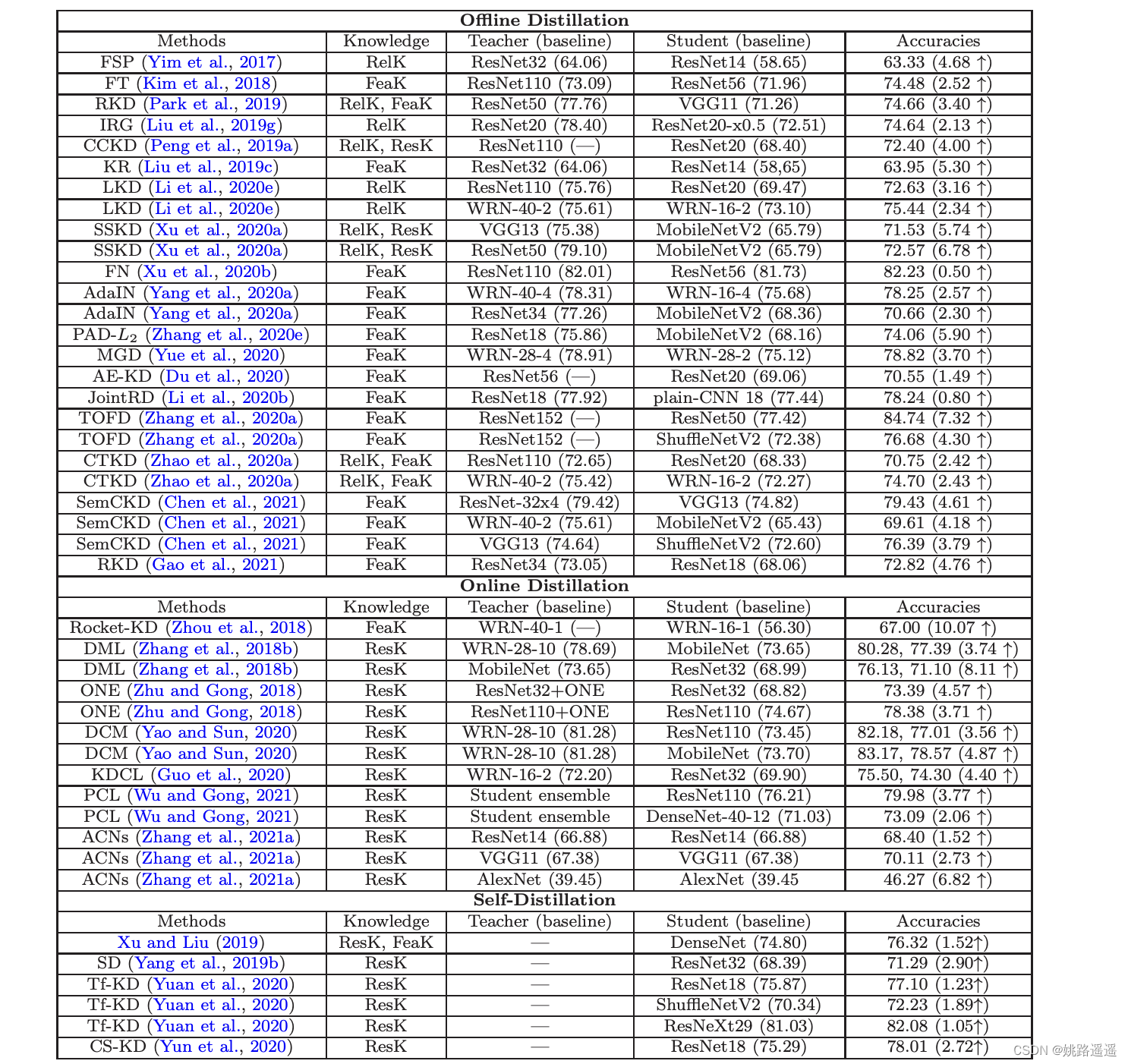
【知识蒸馏】知识蒸馏(Knowledge Distillation)技术详解
参考论文:Knowledge Distillation: A Survey 1.前言 近年来,深度学习在学术界和工业界取得了巨大的成功,根本原因在于其可拓展性和编码大规模数据的能力。但是,深度学习的主要挑战在于,受限制于资源容量࿰…...

公司新招了个腾讯5年经验的测试员,让我见识到什么才是真正的测试天花板····
5年测试,应该是能达到资深测试的水准,即不仅能熟练地开发业务,而且还能熟悉项目开发,测试,调试和发布的流程,而且还应该能全面掌握数据库等方面的技能,如果技能再高些的话,甚至熟悉分…...

(一维、二维)数组传参,(一级、二级)指针传参【含样例分析,新手易懂】
目录数组传参一维数组传参二维数组传参指针传参一级指针传参二级指针传参我们在写代码的时候难免要把数组或者指针传给函数,那函数的参数该如何设计呢? 数组传参 一维数组传参 我们首先来看下面代码的几个例子: #include <stdio.h>…...

for循环中的setTimeout以及var let作用域
看了很多解释,感觉都不好理解。这个文章是我自己的理解,可以做个参考,如果我理解的不对,欢迎在评论区指正: var:使用var声明的变量具有全局作用域 (循环中每次声明的是同一个变量) l…...
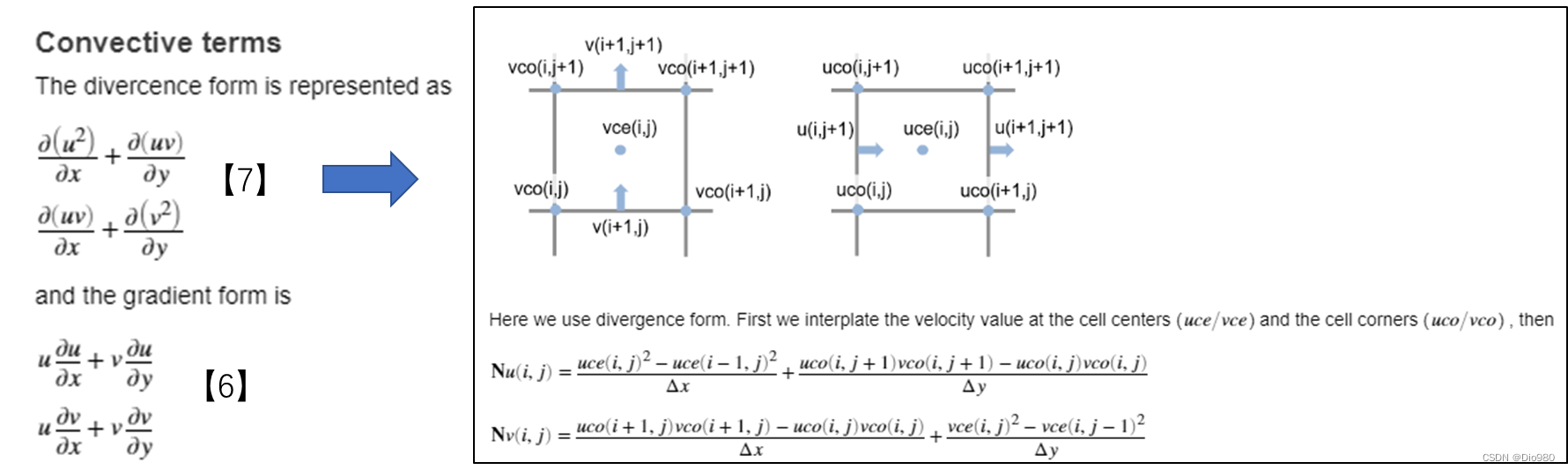
有限差分法求解不可压NS方程
网上关于有限差分法解NS方程的程序实现不尽完备,这里是一些补充注解 现有的优秀资料 理论向 【1】如何从物理意义上理解NS方程? - 知乎 【2】NS方程数值解法:投影法的简单应用 - 知乎 【3】[计算流体力学] NS 方程的速度压力法差分格式_…...
Android入门第66天-使用AOP
开篇这篇恐怕又是一篇补足网上超9成关于这个领域实际都是错的、用不起来的一个知识点了。网上太多太多教程和案例用的是一个叫hujiang的AOP组件-com.hujiang.aspectjx:gradle-android-plugin-aspectjx。首先这些错的文章我不知道是怎么来的,其次那些案例真的运行成功…...

pl/sql篇之触发器
简述本文將具体简述触发器的语法,触发条件及其适用场景,希望对读者理解,使用触发器能起到作用。触发器的定位触发器是数据库独立编译,存储的对象,是数据库重要的技术。和函数不同,触发器的执行是主动的&…...

黑马《数据结构与算法2023版》正式发布
有人的地方就有江湖。 在“程序开发”的江湖之中,各种技术流派风起云涌,变幻莫测,每一位IT侠客,对“技术秘籍”的追求和探索也从未停止过。 要论开发技术哪家强,可谓众说纷纭。但长久以来,确有一技&#…...
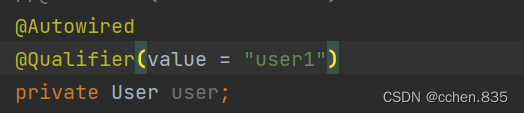
Spring的创建和使用
目录 创建Spring项目 步骤 1)使用Maven的方式创建Spring项目 2)添加Spring依赖 3)创建启动类 存Bean对象 1.创建Bean对象 2.将Bean注册到Spring中 取Bean对象并使用 步骤 1.先得到Spring上下文对象 2.从Spring中获取Bean对象 3.使用Bean ApplicationContext VS Bea…...
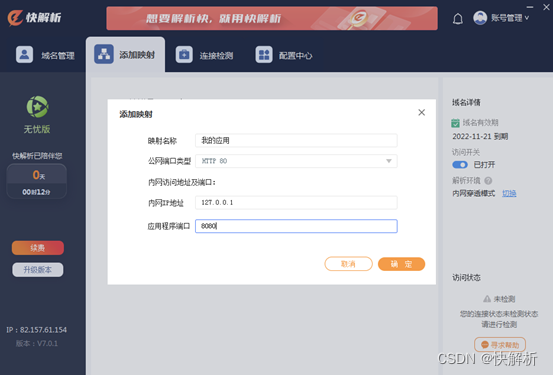
如何实现外网跨网远程控制内网计算机?快解析来解决
远程控制,是指管理人员在异地通过计算机网络异地拨号或双方都接入Internet等手段,连通需被控制的计算机,将被控计算机的桌面环境显示到自己的计算机上,通过本地计算机对远方计算机进行配置、软件安装程序、修改等工作。通俗来讲&a…...

【跟着ChatGPT学深度学习】ChatGPT教我文本分类
【跟着ChatGPT学深度学习】ChatGPT教我文本分类 ChatGPT既然无所不能,我为啥不干脆拜他为师,直接向他学习,岂不是妙哉。说干就干,我马上就让ChatGPT给我生成了一段文本分类的代码,不看不知道,一看吓一跳&am…...

IM即时通讯架构技术:可靠性、有序性、弱网优化等
消息的可靠性是IM系统的典型技术指标,对于用户来说,消息能不能被可靠送达(不丢消息),是使用这套IM的信任前提。 换句话说,如果这套IM系统不能保证不丢消息,那相当于发送的每一条消息都有被丢失的…...

【算法】三道算法题两道难度中等一道困难
算法目录只出现一次的数字(中等难度)java解答参考二叉树的层序遍历(难度中等)java 解答参考给表达式添加运算符(比较困难)java解答参考大家好,我是小冷。 上一篇是算法题目 接下来继续看下算法题…...
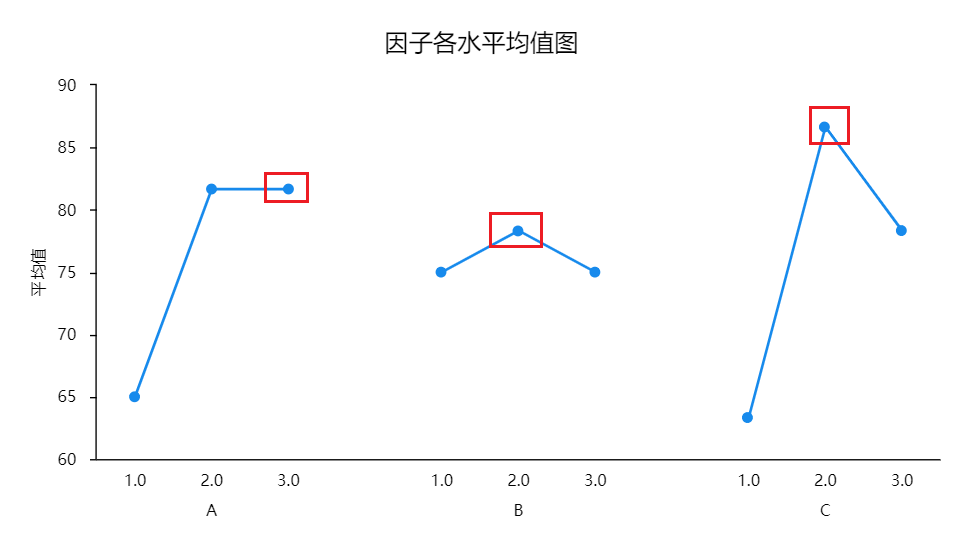
正交实验与极差分析
正交试验极差分析流程如下图: 正交试验说明 正交试验是研究多因素试验的设计方法。对于多因素、多水平的实验要求,如果每个因素的每个水平都要进行试验,这样就会耗费大量的人力和时间,正交试验可以选择出具有代表性的少数试验进行…...
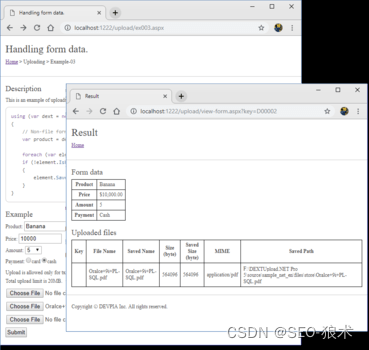
DEXTUpload .NET增强的上传速度和可靠性
DEXTUpload .NET增强的上传速度和可靠性 DEXTUpload.NET Pro托管在Windows操作系统上的Internet Information Server(IIS)上,服务器端组件基于HTTP协议,支持从web浏览器到web服务器的文件上载。它也可以在ASP.NET服务器应用程序平台开发的任何网站上使用…...
)
SkyWalking 将方法加入追踪链路(@Trace)
SkyWalking8 自定义链路追踪@Trace 自定义链路,需要依赖skywalking官方提供的apm-toolkit-trace包.在pom.xml的dependencies中添加如下依赖: <dependency><groupId>org.apache.skywalking</groupId><artifactId>apm-toolkit-trace</artifactId>&…...
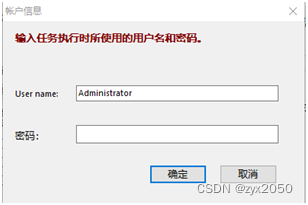
MySQL Administrator定时备份MySQL数据库
1、下载并安装软件mysql-gui-tools-5.0-r17-win32.exe 2、将汉化包zh_CN文件夹拷贝到软件安装目录 3、菜单中打开MySql Adminstrator,见下图,初次打开无服务实例。 点击已存储连接右侧按钮①,打开下图对话框。点击“新连接”按钮ÿ…...

Kubernetes入门教程 --- 使用二进制安装
Kubernetes入门教程 --- 使用二进制安装1. Introduction1.1 架构图1.2 关键字介绍1.3 简述2. 使用Kubeadm Install2.1 申请三个虚拟环境2.2 准备安装环境2.3 配置yum源2.4 安装Docker2.4.1 配置docker加速器并修改成k8s驱动2.5 时间同步2.6 安装组件3. 基础知识3.1 Pod3.2 控制…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
