当前位置： 首页 > news >正文

2023年中国分布式光纤传感产量、需求量及行业市场规模分析[图]

news 2026/2/9 4:22:37

分布式光纤传感器中的光纤能够集传感、传输功能于一体，能够完成在整条光纤长度上环境参量的空间、时间多维连续测量，具有结构简单、易于布设、性价比高、易实现长距离等独特优点，常用的分布式光纤传感器有光时域反射仪、布里渊分析仪、喇曼反射仪。

分布式光纤传感器主要种类

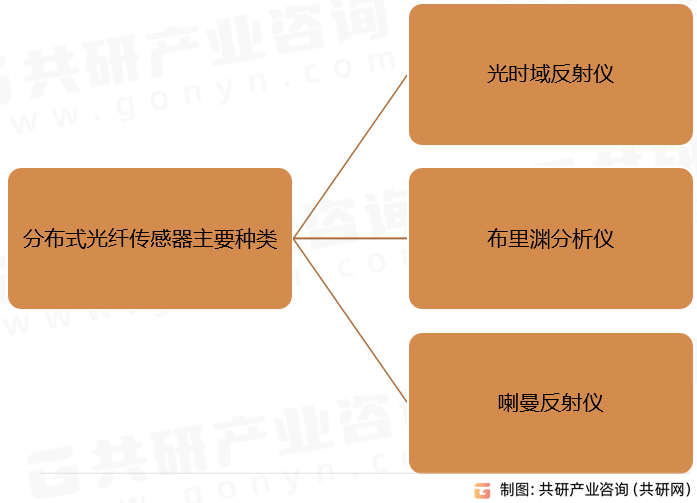
分布式光纤传感器主要种类

资料来源：共研产业咨询（共研网）

分布式光纤传感技术正在蓬勃发展。分布式光纤传感器具有抗电磁干扰、体积小、灵敏度高，尤其是具有实时、多点远程监控的优点，目前已发展成为仪器仪表、消防电子、电力安全保护等领域的重要产品线。分布式光纤传感器需求呈增长趋势，数据显示，2022年国内分布式光纤传感器产量4.25万套，需求量6.15万套。

2014-2023年中国分布式光纤传感器产销量及预测

2014-2023年中国分布式光纤传感器产销量及预测

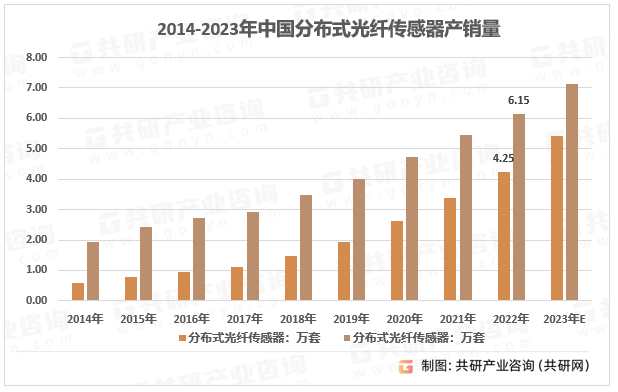
资料来源：共研产业咨询（共研网）

《2023-2029年全球与中国分布式光纤传感市场调查与投资潜力分析报告》为共研产业研究院自主研究发布的行业报告，是分布式光纤传感领域的年度专题报告。分布式光纤传感器特别适用于工作环境恶劣、监测距离长的电网基建、城市管廊、油气能源基建、海底缆线、交通基建、城市安防等领域中，受益于下游应用领域的建设需求，推动了分布式光纤行业的快速发展。2022年中国分布式光纤传感器市场规模达71.2亿元。

2014-2023年中国分布式光纤传感器市场规模及预测

2014-2023年中国分布式光纤传感器市场规模及预测

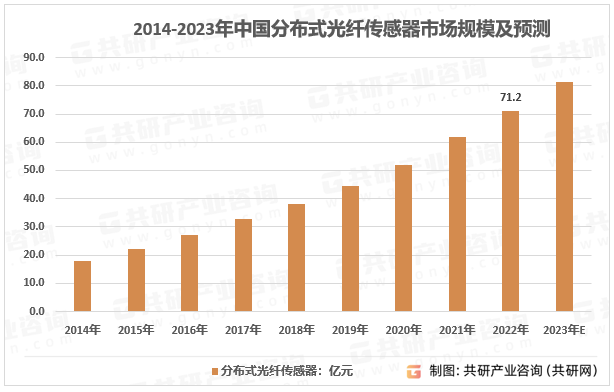
资料来源：共研产业咨询（共研网）

相关文章：

2023年中国分布式光纤传感产量、需求量及行业市场规模分析[图]

分布式光纤传感器中的光纤能够集传感、传输功能于一体，能够完成在整条光纤长度上环境参量的空间、时间多维连续测量，具有结构简单、易于布设、性价比高、易实现长距离等独特优点，常用的分布式光纤传感器有光时域反射仪、布里渊分析仪、喇曼反…...

编程日记 2023/10/15 18:04:59

B2R Raven: 2靶机渗透

B2R Raven: 2靶机渗透 视频参考：ajest ：https://www.zhihu.com/zvideo/1547357583714775040?utm_id0 原文参考：ajest ：https://zhuanlan.zhihu.com/p/270343652 文章目录 B2R Raven: 2靶机渗透1 启动靶机，查看后网卡…...

编程日记 2023/10/15 18:03:58

SpringBoot-黑马程序员-学习笔记（六）

目录 76.常用计量单位使用 77.bean属性校验 81.测试表现层 82.发送虚拟请求 94.springboot读写redis的客户端 100.ElasticSearch（简称ES） 一个分布式全文搜索引擎 76.常用计量单位使用 Data Component ConfigurationProperties(prefix "serve…...

编程日记 2023/10/15 18:02:57

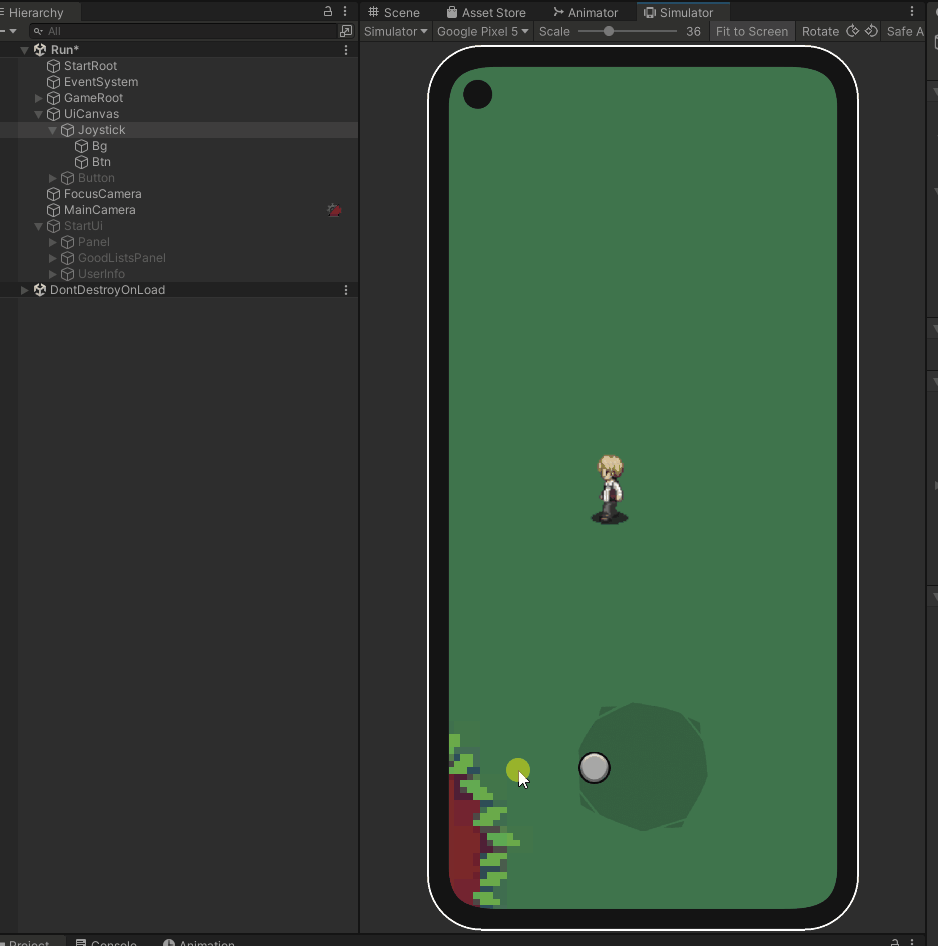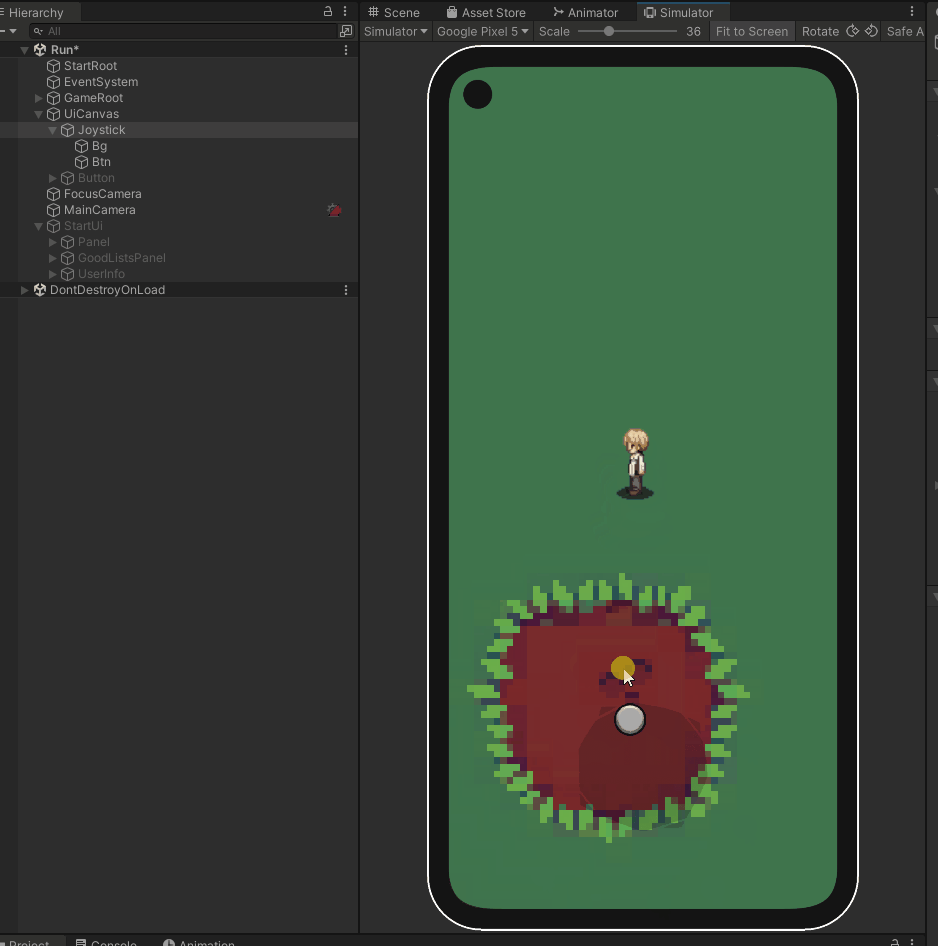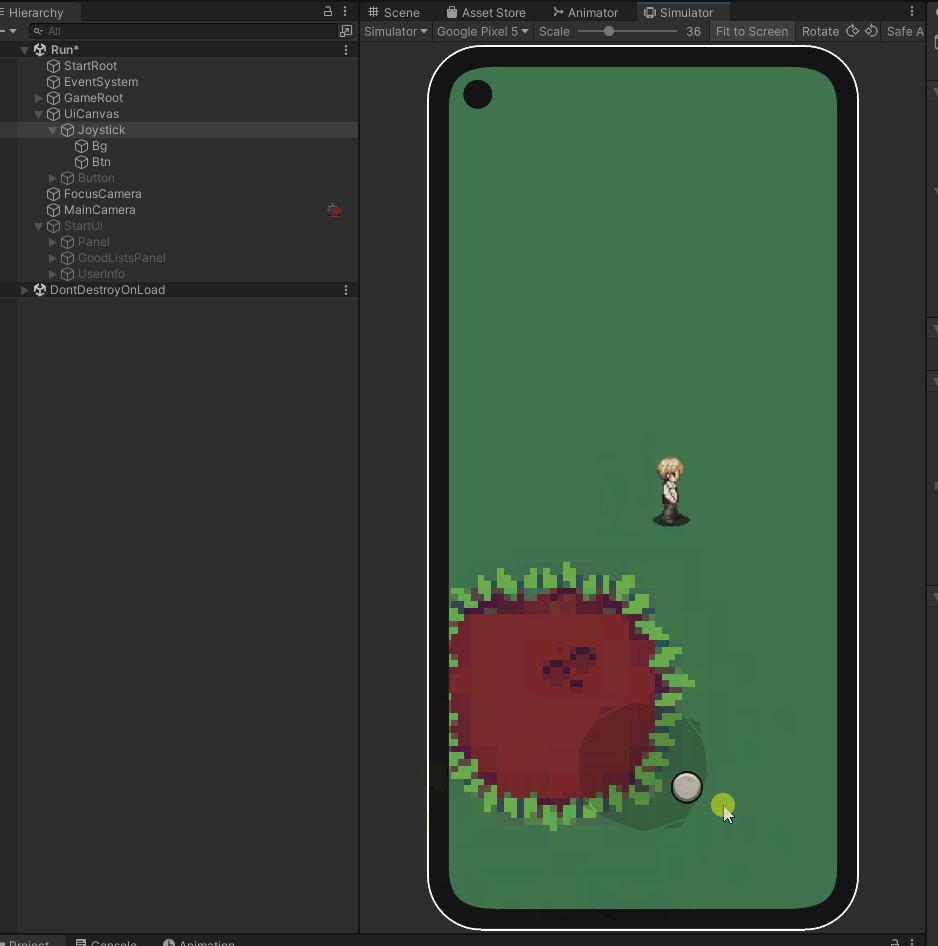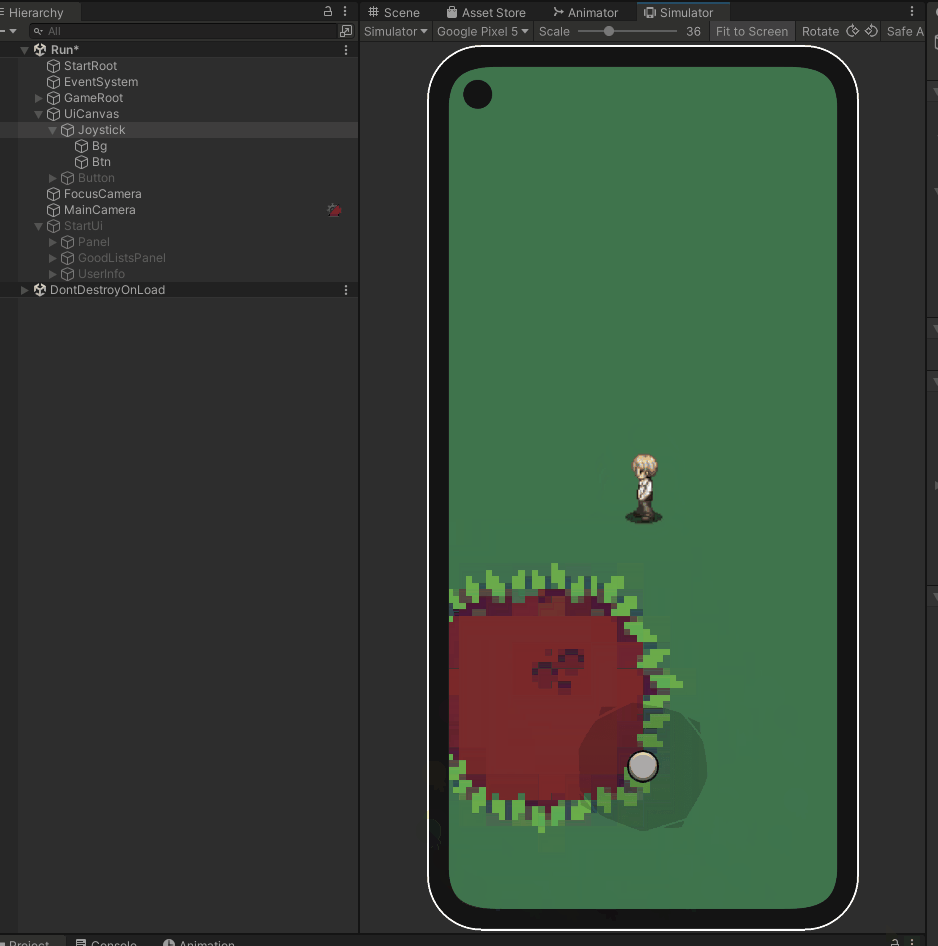
unity2022版本 实现手机虚拟操作杆

简介 在许多移动游戏中，虚拟操纵杆是一个重要的用户界面元素，用于控制角色或物体的移动。本文将介绍如何在Unity中实现虚拟操纵杆，提供了一段用于移动控制的代码。我们将讨论不同类型的虚拟操纵杆，如固定和跟随，以及如…...

编程日记 2023/10/15 18:01:56

『GitHub Actions』部署静态博客指南

前言 之前博主是使用的 Jenkins 实现 vuepress 博客的自动部署与持续交付，但是因为现在迁移服务器到海外，并且服务器配置降低。现在经常出现服务器的 Jenkins 构建过程中 CPU 占用率过高，导致服务器卡死 然后我想的话既然只是部署静态博客&…...

编程日记 2023/10/15 18:00:55

WPF Datagrid Header数据绑定，表头复选框实现全选、全否、部分选中，根据条目动态变化

制作一个根表头为CheckBox可全选、全不选的列表，且可根据条目自动调整CheckBox的状态（选中、不选、部分选中）。 本来是想用DataGrid做一个CheckBox的列用于勾选其中的某些行，当时做出来之后想着添加一个全选、全否的功能。做两个…...

编程日记 2023/10/15 17:59:54

Tensorflow2 中对模型进行编译，不同loss函数的选择下输入数据格式需求变化

一、tf2中常用的损失函数介绍 在 TensorFlow 2 中，编译模型时可以选择不同的损失函数来定义模型的目标函数。不同的损失函数适用于不同的问题类型和模型架构。下面是几种常见的损失函数以及它们的作用和适用场景： 1.均方误差（Mean Squared …...

编程日记 2023/10/15 17:58:53

【python】基础语法（三）--异常、模块、包

异常 代码中出现的报错问题，可能会导致整个代码的停止，为了避免这种情况，有了捕获异常操作； 捕获异常 提前预知可能出错的代码，做好准备，避免因bug导致整个项目停止； try：可能出…...

编程日记 2023/10/15 17:57:52

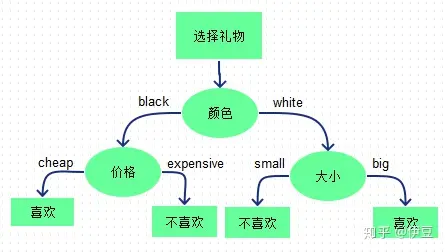
XGBoost+LR融合

1、背景简介 xgboostlr模型融合方法用于分类或者回归的思想最早由facebook在广告ctr预测中提出，其论文Practical Lessons from Predicting Clicks on Ads at Facebook有对其进行阐述。在这篇论文中他们提出了一种将xgboost作为feature transform的方法。大概的思想…...

编程日记 2023/10/15 17:56:51

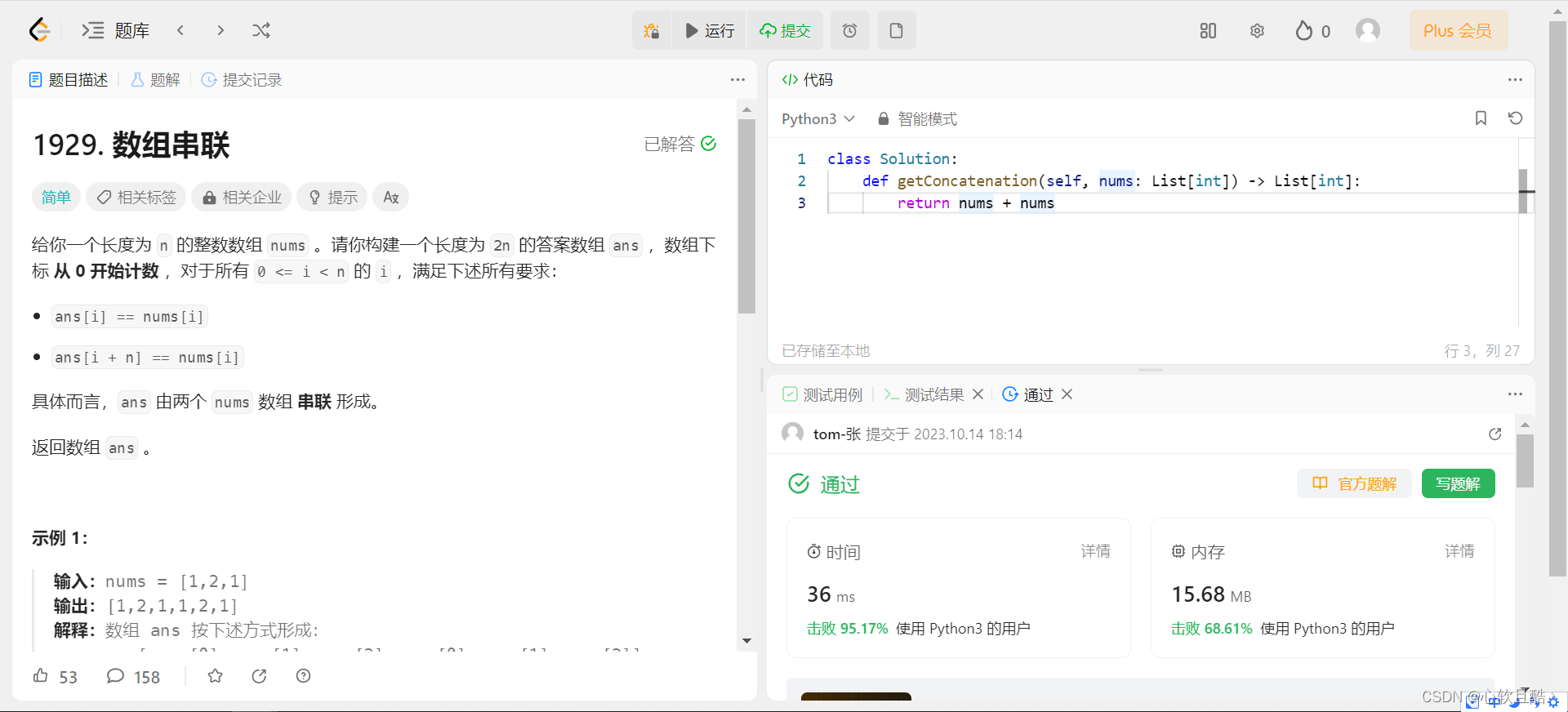
leetcode:1929. 数组串联(python3解法)

难度&#xff1a;简单 给你一个长度为 n 的整数数组 nums 。请你构建一个长度为 2n 的答案数组 ans &#xff0c;数组下标 从 0 开始计数 &#xff0c;对于所有 0 < i < n 的 i &#xff0c;满足下述所有要求&#xff1a; ans[i] nums[i]ans[i n] nums[i] 具体而言&am…...

编程日记 2023/10/15 17:55:49

Epoch和episodes的区别

“Epoch” 和 “episode” 是两个不同的概念&#xff0c;通常在不同领域中使用。 Epoch&#xff08;周期&#xff09;&#xff1a; Epoch 是一个在机器学习和深度学习中常用的术语&#xff0c;通常用于表示训练数据集中的一个完整遍历。在每个 epoch 中&#xff0c;整个训练数据…...

编程日记 2023/10/15 17:54:46

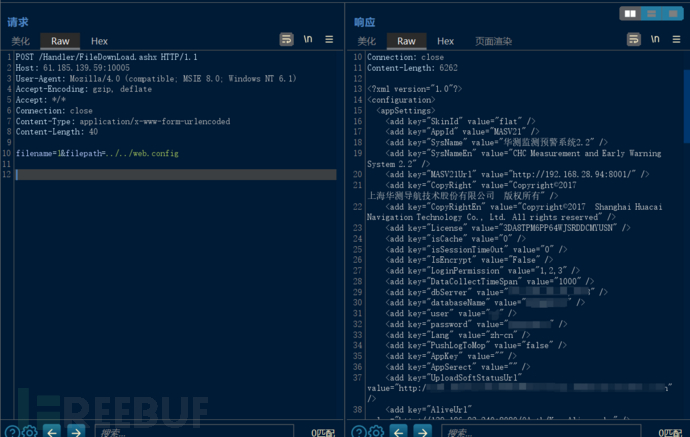
漏洞复现--华测监测预警系统2.2任意文件读取

免责声明&#xff1a; 文章中涉及的漏洞均已修复&#xff0c;敏感信息均已做打码处理&#xff0c;文章仅做经验分享用途&#xff0c;切勿当真&#xff0c;未授权的攻击属于非法行为&#xff01;文章中敏感信息均已做多层打马处理。传播、利用本文章所提供的信息而造成的任何直…...

编程日记 2023/10/15 17:53:45

数据结构 - 6（优先级队列（堆）13000字详解）

一&#xff1a;堆 1.1 堆的基本概念 堆分为两种&#xff1a;大堆和小堆。它们之间的区别在于元素在堆中的排列顺序和访问方式。 大堆&#xff08;Max Heap&#xff09;&#xff1a; 在大堆中&#xff0c;父节点的值比它的子节点的值要大。也就是说&#xff0c;堆的根节点是堆…...

编程日记 2023/10/15 17:52:44

Js高级技巧—拖放

拖放基本功能实现 拖放是一种非常流行的用户界面模式。它的概念很简单&#xff1a;点击某个对象&#xff0c;并按住鼠标按钮不放&#xff0c;将 鼠标移动到另一个区域&#xff0c;然后释放鼠标按钮将对象“放”在这里。拖放功能也流行到了 Web 上&#xff0c;成为 了一些更传统…...

编程日记 2023/10/15 17:51:43

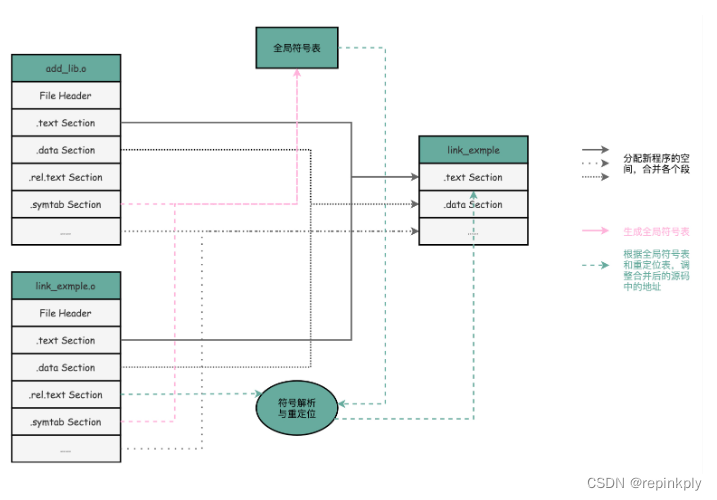
ELF和静态链接：为什么程序无法同时在Linux和Windows下运行？

目录 疑问 编译、链接和装载&#xff1a;拆解程序执行 ELF 格式和链接&#xff1a;理解链接过程 小结 疑问 既然我们的程序最终都被变成了一条条机器码去执行&#xff0c;那为什么同一个程序&#xff0c;在同一台计算机上&#xff0c;在 Linux 下可以运行&#xff0c;而在…...

编程日记 2023/10/15 17:50:42

【爬虫实战】python微博热搜榜Top50

一.最终效果 二.项目代码 2.1 新建项目 本文使用scrapy分布式、多线程爬虫框架编写的高性能爬虫&#xff0c;因此新建、运行scrapy项目3步骤&#xff1a; 1.新建项目: scrapy startproject weibo_hot 2.新建 spider: scrapy genspider hot_search "weibo.com" 3…...

编程日记 2023/10/15 17:49:40

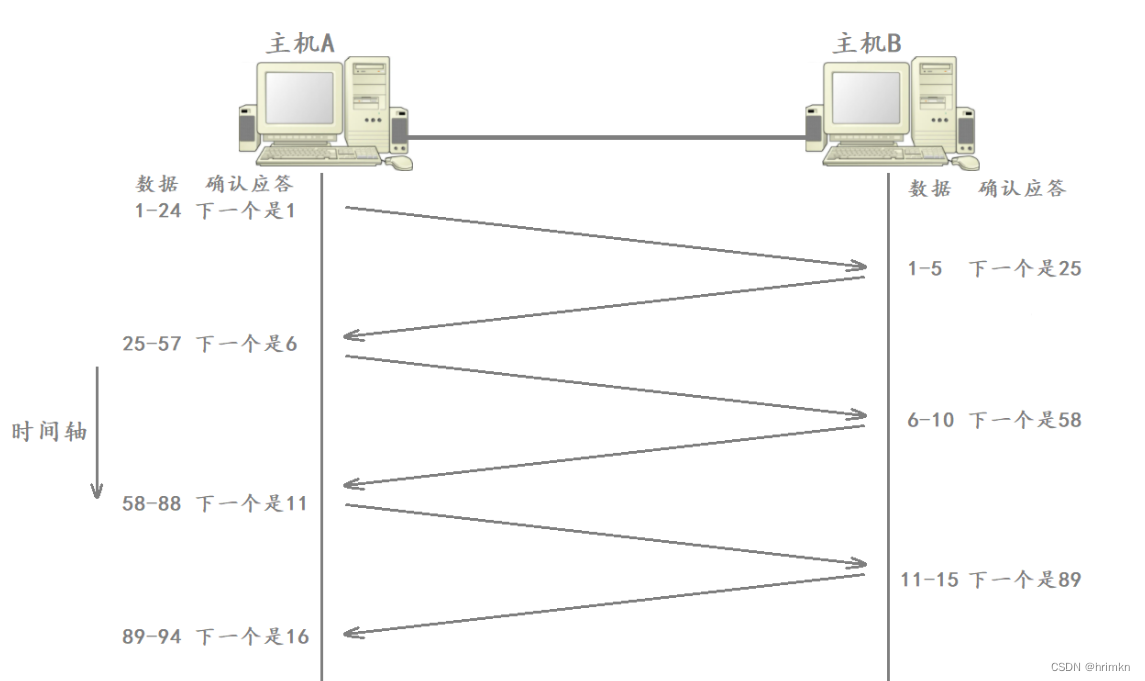
【网络基础】——传输层

目录 前言 传输层 端口号 端口号范围划分 知名端口号 进程与端口号的关系 netstat UDP协议 UDP协议位置 UDP协议格式 UDP协议特点 面向数据报 UDP缓冲区 UDP的使用注意事项 基于UDP的应用层协议 TCP协议 TCP简介 TCP协议格式 确认应答机制&#…...

编程日记 2023/10/15 17:48:38

删除字符串特定的字符（fF）C语言

代码&#xff1a; #include <stdio.h> void funDel(char *str) {int i, j;for (i j 0; str[i] ! \0; i)if (str[i] ! f && str[i] ! F)str[j] str[i];str[j] \0; }int main() {char str[100];printf("请输入一个字符串&#xff1a;");gets(str);pr…...

编程日记 2023/10/15 17:47:38

C++入门(1)：命名空间，IO流 输入输出，缺省参数

一、命名空间 1.1 命名空间的作用&#xff1a; ​ 避免标识符命名冲突 1.2 命名空间定义&#xff1a; 关键字&#xff1a;namespace namespace test {// 命名空间内可以定义变量/函数/类型int a 10;int Add(int x, int y){return x y;}struct Stack{int* a;int top;int …...

编程日记 2023/10/15 17:45:36

Go 语言面试题（三）：并发编程

文章目录 Q1 无缓冲的 channel 和 有缓冲的 channel 的区别&#xff1f;Q2 什么是协程泄露(Goroutine Leak)&#xff1f;Q3 Go 可以限制运行时操作系统线程的数量吗&#xff1f; Q1 无缓冲的 channel 和 有缓冲的 channel 的区别&#xff1f; 对于无缓冲的 channel&#xff0c…...

编程日记 2023/10/15 17:43:34

调用支付宝接口响应40004 SYSTEM_ERROR问题排查

在对接支付宝API的时候&#xff0c;遇到了一些问题&#xff0c;记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

编程新知 2026/2/8 20:41:48

微信小程序之bind和catch

这两个呢&#xff0c;都是绑定事件用的&#xff0c;具体使用有些小区别。 官方文档&#xff1a; 事件冒泡处理不同 bind&#xff1a;绑定的事件会向上冒泡&#xff0c;即触发当前组件的事件后&#xff0c;还会继续触发父组件的相同事件。例如&#xff0c;有一个子视图绑定了b…...

编程新知 2026/2/5 5:05:56

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例

使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件&#xff0c;常用于在两个集合之间进行数据转移&#xff0c;如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model&#xff1a;绑定右侧列表的值&…...

编程新知 2026/2/4 4:25:40

【HarmonyOS 5.0】DevEco Testing：鸿蒙应用质量保障的终极武器

——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的​​一体化测试平台​​&#xff0c;覆盖应用全生命周期测试需求&#xff0c;主要提供五大核心能力&#xff1a; ​​测试类型​​​​检测目标​​​​关键指标​​功能体验基…...

编程新知 2026/1/28 8:17:53

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序

一、开发准备 ​​环境搭建​​&#xff1a; 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 ​​项目创建​​&#xff1a; File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

编程新知 2025/9/5 12:16:40

反射获取方法和属性

Java反射获取方法 在Java中&#xff0c;反射&#xff08;Reflection&#xff09;是一种强大的机制&#xff0c;允许程序在运行时访问和操作类的内部属性和方法。通过反射&#xff0c;可以动态地创建对象、调用方法、改变属性值&#xff0c;这在很多Java框架中如Spring和Hiberna…...

编程新知 2025/11/9 2:57:17

vue3+vite项目中使用.env文件环境变量方法

vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量&#xff0c;这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

编程新知 2026/1/26 19:12:01

全志A40i android7.1 调试信息打印串口由uart0改为uart3

一&#xff0c;概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本&#xff1a;2014.07&#xff1b; Kernel版本&#xff1a;Linux-3.10&#xff1b; 二&#xff0c;Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01)&#xff0c;并让boo…...

编程新知 2026/2/5 6:28:09

docker 部署发现spring.profiles.active 问题

报错&#xff1a; org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

编程新知 2025/9/20 12:14:18

AI，如何重构理解、匹配与决策？

AI 时代&#xff0c;我们如何理解消费&#xff1f; 作者&#xff5c;王彬 封面&#xff5c;Unplash 人们通过信息理解世界。 曾几何时&#xff0c;PC 与移动互联网重塑了人们的购物路径&#xff1a;信息变得唾手可得&#xff0c;商品决策变得高度依赖内容。 但 AI 时代的来…...

编程新知 2026/1/30 2:33:11