字符串思维题练习 DAY6 (CF 245H , CF 559B , CF 1731C , CF1109B)
字符串思维题练习 DAY6 (CF 245H , CF 559B , CF 1731C , CF1109B)
CF 245 H. Queries for Number of Palindromes(字符串 + dp)
Problem - H - Codeforces
大意:给出一个字符串S (|S| ≤ 5000) , 给出 Q 次询问 , 每次询问 S 的一个区间 [l , r] , 求区间字符串的回文子串个数。
思路:一开始考虑了 马拉车 ,求出每个位置作为回文中心的最大回文半径 , 但是这样的话每次询问都要遍历区间[l , r] 去更新每一个回文中心所对应的回文半径 , 复杂度
O ( ∑ i = 1 Q ( r i − l i ) ) O(\sum_{i=1}^{Q}(r_i-l_i) ) O(i=1∑Q(ri−li))
显然是不能接受的 , 考虑 O(N^2) 预处理 , O(1) 回答询问
a n s [ i ] [ j ] 为 [ l , r ] 的答案 ans[i][j] ~为[l , r]的答案 ans[i][j] 为[l,r]的答案
考虑转移
a n s [ l ] [ r ] = a n s [ l ] [ r − 1 ] + p r e [ l ] [ r ] ans[l][r]=ans[l][r-1]+pre[l][r] ans[l][r]=ans[l][r−1]+pre[l][r]
pre[l][r] 是右边界为 r , 左边界 ≥ l 所有字符串中回文串的个数
p r e [ l ] [ r ] = p r e [ l ] [ r − 1 ] + d p [ l ] [ r ] pre[l][r] = pre[l][r-1]+dp[l][r] pre[l][r]=pre[l][r−1]+dp[l][r]
dp[l][r] 为 [l , r] 这个区间的字符串是否为回文串
所以显而易见问题就变成了就 dp[l][r] , 有两种求法
第一种 : 区间dp
不难看出我们要求的是一个个区间 , 且区间之间存在转移关系 , 所以可以使用区间 dp 进行转移。
初始化:初始化奇回文和偶回文 , 显然所有长度为一的区间都为回文区间 , 长度为二的区间判断是否回文即可。
转移方程: d p [ l ] [ r ] ∣ = ( d p [ l + 1 ] [ r − 1 ] & & ( s [ l ] = = s [ r ] ) ) 转移方程:dp[l][r] |= (dp[l + 1][r - 1] ~~\&\&~~ (s[l] == s[r])) 转移方程:dp[l][r]∣=(dp[l+1][r−1] && (s[l]==s[r]))
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
//#define int long long
const int INF = 9e18;
const int N = 5e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int ans[N][N] , pre[N][N];
bool dp[N][N];
int n , q;
string s;signed main(){IOScin >> s;n = s.size();s = '?' + s;for(int i = 1 ; i <= n ; i ++) dp[i][i] = 1;for(int i = 1 ; i < n ; i ++) dp[i][i + 1] = (s[i] == s[i + 1]);for(int len = 3 ; len <= n ; len ++) {for(int l = 1 ; l <= n ; l ++) {int r = l + len - 1;dp[l][r] |= (dp[l + 1][r - 1] && (s[l] == s[r]));}}for(int r = 1 ; r <= n ; r ++) {for(int l = r ; l >= 1 ; l --){pre[l][r] = pre[l + 1][r] + dp[l][r];}}for(int l = 1 ; l <= n ; l ++) {for(int r = l ; r <= n ; r ++) {ans[l][r] = ans[l][r - 1] + pre[l][r];}}cin >> q;while(q --) {int l , r;cin >> l >> r;cout << ans[l][r] << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
第二种:马拉车
马拉车的思路比较直接 , 求出每个回文中心对应的回文半径的长度 , 以当前回文中心更新即可。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
//#define int long long
//const int INF = 9e18;
const int N = 5e3 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int ans[N][N] , pre[N][N];
bool dp[N][N];
int n , q , m;
string s , t;int d[N * 2 + 1];
//给出一个字符串求d[i]数组并返回马拉车串
string manacher(string s){string now = "#$";int n = s.size();for(int i = 0 ; i < n ; i ++) now += s[i] , now += '$';n = now.size();d[1] = 1;for(int i = 2 , l , r = 1; i < n ; i ++){if(i <= r) d[i] = min(d[r - i + l] , r - i + 1);else d[i] = 1;while(now[i - d[i]] == now[i + d[i]]) d[i] += 1;if(i + d[i] - 1 > r) l = i - d[i] + 1 , r = i + d[i] - 1; }return now;
}void watch(string s){int n = s.size();for(int i = 0 ; i < n ; i ++) cout << s[i] << " ";cout << "\n"; for(int i = 0 ; i < n ; i ++) cout << d[i] << " ";cout << "\n";
}signed main(){IOScin >> s;n = s.size();t = manacher(s);m = t.size();
// watch(s); int len = 0 , l = 0 , r = 0;for(int i = 1 ; i <= m ; i ++) {if(i & 1) {//偶回文中心len = (d[i] - 1) / 2;l = (i - 1) / 2;r = (i + 1) / 2;} else {len = d[i] / 2;l = r = i / 2;}for(int i = 1 ; i <= len ; i ++ , l -= 1 , r += 1) {dp[l][r] = 1;}}for(int r = 1 ; r <= n ; r ++) {for(int l = r ; l >= 1 ; l --){pre[l][r] = pre[l + 1][r] + dp[l][r];}}for(int l = 1 ; l <= n ; l ++) {for(int r = l ; r <= n ; r ++) {ans[l][r] = ans[l][r - 1] + pre[l][r];}}cin >> q;while(q --) {int l , r;cin >> l >> r;cout << ans[l][r] << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
CF 559 B. Equivalent Strings(哈希+搜索剪枝)
Problem - B - Codeforces
大意:两个等长的字符串 a , b(条件相等)需要满足以下两个条件其一:
1 : 两个字符串相等
2: 字符串 a 可以分为等长的 a1 , a2 , 字符串 b 可以分为等长的 b1 b2 。满足 a1 与 b1(条件相等)a2 与 b2(条件相等)或者 a1 与 b2 (条件相等) a2 与 b1 (条件相等)。
给出两个登场字符串判断是否条件相等。
思路:不难看出这个条件相等是一个递归的定义 , 考虑递归搜索,哈希比较区间字符串。不妨计算一下递归搜索的复杂度。
首先考虑搜索的深度 , 由于每次往下走一层区间的长度减半 , 所以最多搜索 log(2e5) = 18 层 , 每次搜索 , 每个状态会分裂为四个状态即比较(a1 , b1) (a2 , b2) (a1 , b2) (a2 , b1) , 比较的次数为 4^18 = 6e15 , 非常恐怖的复杂度。
考虑搜索剪枝:
剪枝1 : 两个条件相等的区间字符的种类数和每种的个数相等 , 考虑前缀和处理 , O(1) 查询区间的字符个数 , 每次搜索之前判断一下是否相等。
剪枝2:对于每一层 , 满足两个条件其中一个当前区间的字符串即为条件相等 , 不用再去搜另外一颗子树。
加上两个剪枝后实测能跑 900ms , 时限 2s
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int INF = 9e18;
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;#define ull unsigned long long
const int Base = 131;
ull base[N] , hx[N] , hy[N];
string x , y;
int n;
int cntx[N][2] , cnty[N][2];
//-------------------------------------------------------------
//求[l , r) 的散列值 (从 0 开始)
inline ull get_x(int l,int r){return hx[r] - hx[l] * base[r - l];
}
inline ull get_y(int l,int r){return hy[r] - hy[l] * base[r - l];
}bool ask(int lx , int rx , int ly , int ry) {lx += 1;ly += 1;rx += 1;ry += 1;return (cntx[rx][0] - cntx[lx - 1][0] != cnty[ry][0] - cnty[ly - 1][0]) || (cntx[rx][1] - cntx[lx - 1][1] != cnty[ry][1] - cnty[ly - 1][1]);
}/*
哈希 + 递归搜索剪枝
两次剪枝
*/bool judge(int lx , int rx , int ly , int ry) {if(get_x(lx , rx + 1) == get_y(ly , ry + 1)) return 1;else {int len = rx - lx + 1;if(len & 1) {return 0;} else {int mid = len / 2;bool tag1 = 0 , tag2 = 0;if(ask(lx , lx + mid - 1 , ly , ly + mid - 1) || ask(lx + mid , rx , ly + mid , ry)) tag1 = 0;else tag1 = (judge(lx , lx + mid - 1 , ly , ly + mid - 1) && judge(lx + mid , rx , ly + mid , ry));if(tag1) return 1;if(ask(lx , lx + mid - 1 , ly + mid , ry) || ask(lx + mid , rx , ly , ly + mid - 1)) tag2 = 0;else tag2 = (judge(lx , lx + mid - 1 , ly + mid , ry) && judge(lx + mid , rx , ly , ly + mid - 1));if(tag2) return 1;return 0;}}
}signed main(){cin >> x >> y;n = x.size();base[0] = 1;for(int i = 1 ; i <= n ; i ++) base[i] = base[i - 1] * Base;hx[0] = 0;for(int i = 1 ; i <= n ; i ++) {hx[i] = hx[i - 1] * Base + x[i - 1];cntx[i][0] = cntx[i - 1][0] + (x[i - 1] == 'a');cntx[i][1] = cntx[i - 1][1] + (x[i - 1] == 'b');}hy[0] = 0;for(int i = 1 ; i <= n ; i ++) {hy[i] = hy[i - 1] * Base + y[i - 1];cnty[i][0] = cnty[i - 1][0] + (y[i - 1] == 'a');cnty[i][1] = cnty[i - 1][1] + (y[i - 1] == 'b');}if(judge(0 , n - 1 , 0 , n - 1)) {cout << "YES\n";} else {cout << "NO\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
CF 1731 C. Even Subarrays(枚举剪枝)
Problem - C - Codeforces
大意:给出一个序列 , 求有多少个子区间异或和不为平方数。
转化问题 , 原题 = 总子区间个数 - 异或和为平方数的子区间个数 , 所以要求异或和为平方数的子区间个数。
思路:显然区间异或和能组成的平方数是有限的 , 最多有 根号个的 , 所以我们不妨对于每一个右边界记录合法的左边界的个数 , 合法的左边界即枚举每一个可能组成的平方数 ,根据 pre[l - 1] = pre[r] ^ x , 求出合法的左边界的前缀状态 , 计数即可。
复杂度 O ( n n ) 复杂度O(n\sqrt n) 复杂度O(nn)
注意:坑点在于异或和能表示的范围和状态记录的范围数组开的大小 , 要注意。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int INF = 9e18;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;/*
ans = all - 区间异或值为平方数的区间个数
*/int n , t , a[N];
int v[N] , cnt;signed main(){IOScin >> t;while(t --) {cin >> n;for(int i = 1 ; i <= n ; i ++) {cin >> a[i];}cnt = 0;v[++cnt] = 0;for(int i = 1 ; i * i <= 2 * n ; i ++) v[++cnt] = i * i;//注意思考这里的空间为什么开四倍vector<int>pre(4 * n + 1);int res = 0 , ans = (n + 1) * n / 2 , now = 0;pre[0] = 1;for(int i = 1 ; i <= n ; i ++) {now ^= a[i];for(int j = 1 ; j <= cnt ; j ++) {res += pre[now ^ v[j]];} pre[now] += 1;}cout << ans - res << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
CF 1109 B. Sasha and One More Name(思维)
Problem - B - Codeforces
大意:给出一个回文字符串 , 求最小的分割次数 k , 将当前回文串分割为 k + 1 部分 , 然后重排这 k + 1 部分 , 能得到一个新的回文字符串。
思路:考虑当前字符串是否存在的一个长度 ≤ len / 2 的前缀位置不是当前字符串的border , 如果存在 , 显然 k = 2 的花费就能解决 , 如果不存在 , 手模一下发现不可能存在答案。
对于比 k = 2 更优的答案即 k = 1 的情况 , 考虑暴力枚举分割位置 , 检验方案是否合理 , 复杂度O(n^2);
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int INF = 9e18;
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int nex[N];void init(string s){int len = s.size();nex[1] = 0;for(int i = 2 ; i <= len ; i ++){nex[i] = nex[i-1];while(nex[i] && s[nex[i]] != s[i-1]) nex[i] = nex[nex[i]];nex[i] += (s[i-1] == s[nex[i]]);}
}string s;
int n;signed main(){cin >> s;n = s.size();init(s);bool ok = 0;int ans = -1;vector<bool>tag(n + 1);int now = nex[n];while(now) {tag[now] = 1;now = nex[now];}string now_s , now_k;for(int i = 1 ; i < n ; i ++) {now_s = s.substr(i) + s.substr(0 , i);if(now_s == s) continue;now_k = now_s;reverse(now_k.begin() , now_k.end());if(now_s != now_k) continue;ok = 1; }if(ok == 1) {ans = 1;} else {for(int i = 1 ; i <= n / 2 ; i ++) if(!tag[i]) ans = 2;}if(ans == -1) {cout << "Impossible\n";} else {cout << ans << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
)
字符串思维题练习 DAY6 (CF 245H , CF 559B , CF 1731C , CF1109B)
字符串思维题练习 DAY6 (CF 245H , CF 559B , CF 1731C , CF1109B) CF 245 H. Queries for Number of Palindromes(字符串 dp) Problem - H - Codeforces 大意:给出一个字符串S (|S| ≤ 5000) , 给出 Q 次询问 , 每…...
Linux:Mac VMware Fusion13以及CentOS7安装包
Linux:Mac VMware Fusion13以及CentOS7安装包 1. Mac VMware Fusion132. CentOS7安装包3. 安装 1. Mac VMware Fusion13 下载官网地址:https:www.vmware.com/products/fusion/fusion-evaluation.html 2. CentOS7安装包 注意是m芯片需要使用arm架构的i…...

【微服务部署】十、使用Docker Compose搭建高可用Redis集群
现如今,业务系统对于缓存Redis的依赖似乎是必不可少的,我们可以在各种各样的系统中看到Redis的身影。考虑到系统运行的稳定性,Redis的应用和MySQL数据库一样需要做到高可用部署。 一、Redis 的多种高可用方案 常见的Redis的高可用方案有以下…...

【数据结构】树状数组C++详解
文章目录 引入树状数组定义什么是单点修改和区间查询工作原理区间查询代码实现单点修改实现代码242. 一个简单的整数问题AC代码如下:练习:AC代码如下:引入 242. 一个简单的整数问题 给定长度为 N的数列 A A A<...
机器人制作开源方案 | 扫地机器人
1. 功能描述 扫地机器人是现代家庭清洁的得力助手,能够自主规划清扫路径,避开障碍物,有效覆盖整个清洁区域。扫地机器人的出现极大地减轻了家庭清洁的负担,节省了时间和精力,它可以定期清理地面,确保家居环…...
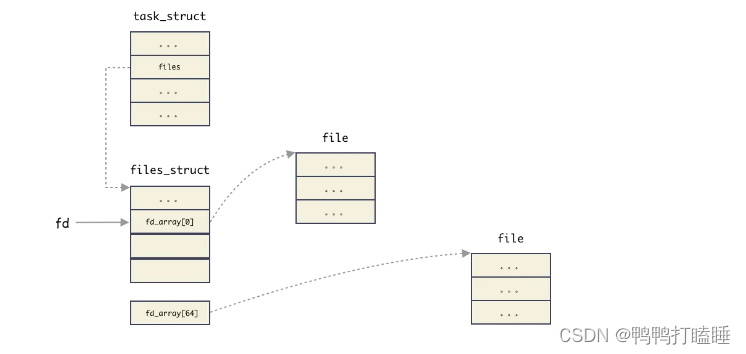
10.2手动推导linux中file, cdev, inode之间的关系
是时候可以手动推导一下linux里面基类父类和子类的关系了 代码放最后把 简单说明版 详细流程 第一步注册驱动 cdev结构体能看做是一个基类,那么链表里面都是字符设备驱动的cdev连载一起,啥串口,lcd的,通过cdev->list_head连接 那cdev结构体里有主次设备号 第一步 使用r…...

JavaScript基础知识13——运算符:一元运算符,二元运算符
哈喽,大家好,我是雷工。 JavaScript的运算符可以根据所需表达式的个数,分为一元运算符、二元运算符、三元运算符。 一、一元运算符 1、一元运算符:只需要一个表达式就可以运算的运算符。 示例:正负号 一元运算符有两…...
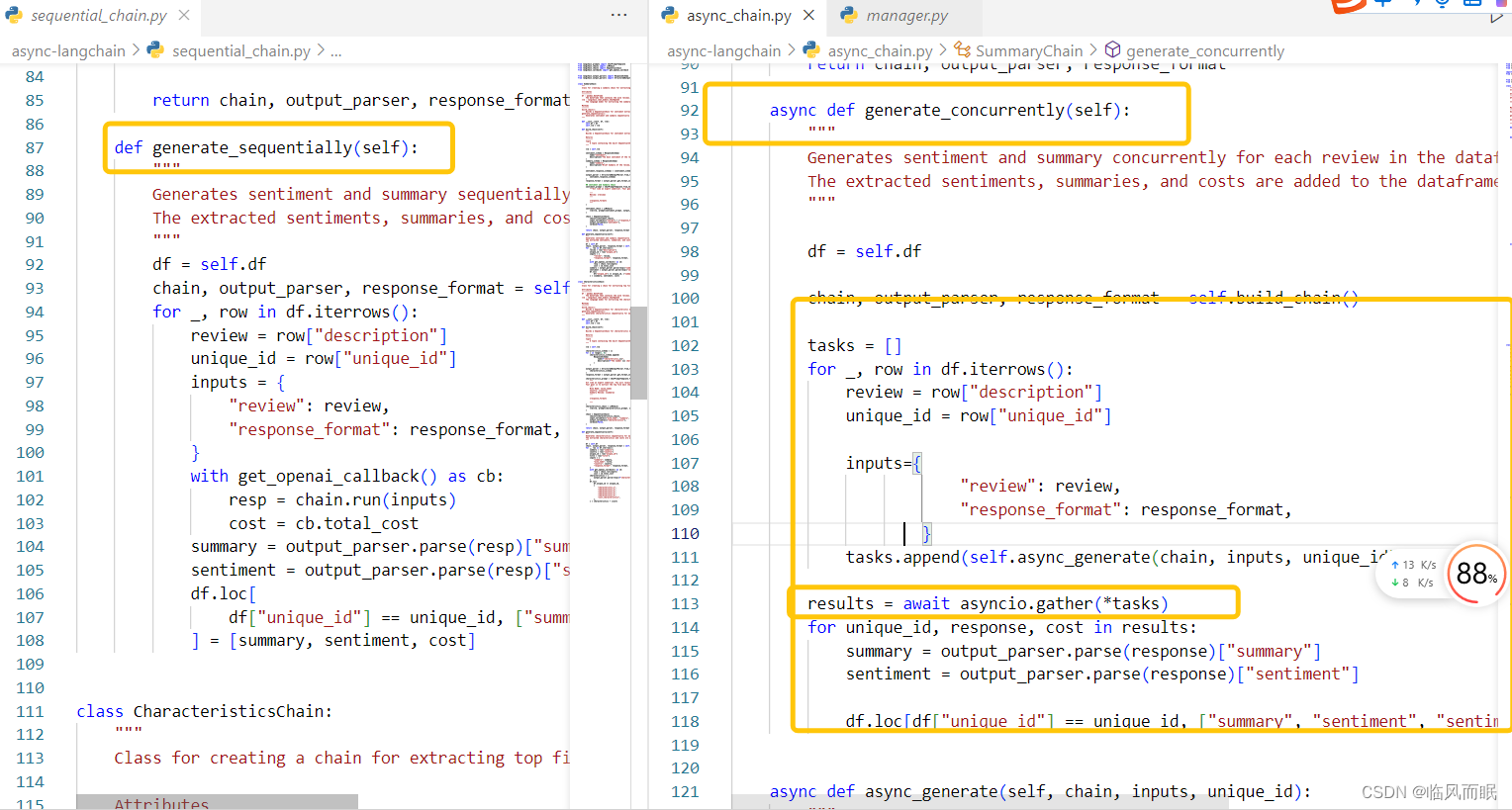
异步使用langchain
文章目录 一.先利用langchain官方文档的AI功能问问二.langchain async api三.串行,异步速度比较 一.先利用langchain官方文档的AI功能问问 然后看他给的 Verified Sources 这个页面里面虽然有些函数是异步函数,但是并非专门讲解异步的 二.langchain asy…...

抖音开放平台第三方代小程序开发,授权事件、消息与事件通知总结
大家好,我是小悟 关于抖音开放平台第三方代小程序开发的两个事件接收推送通知,是开放平台代小程序实现业务的重要功能。 授权事件推送和消息与事件推送类型都以Event的值判断。 授权事件推送通知 授权事件推送包括:推送票据、授权成功、授…...
华为9.20笔试 复现
第一题 丢失报文的位置 思路:从数组最小索引开始遍历 #include <iostream> #include <vector> using namespace std; // 求最小索引值 int getMinIdx(vector<int> &arr) {int minidx 0;for (int i 0; i < arr.size(); i){if (arr[i] …...
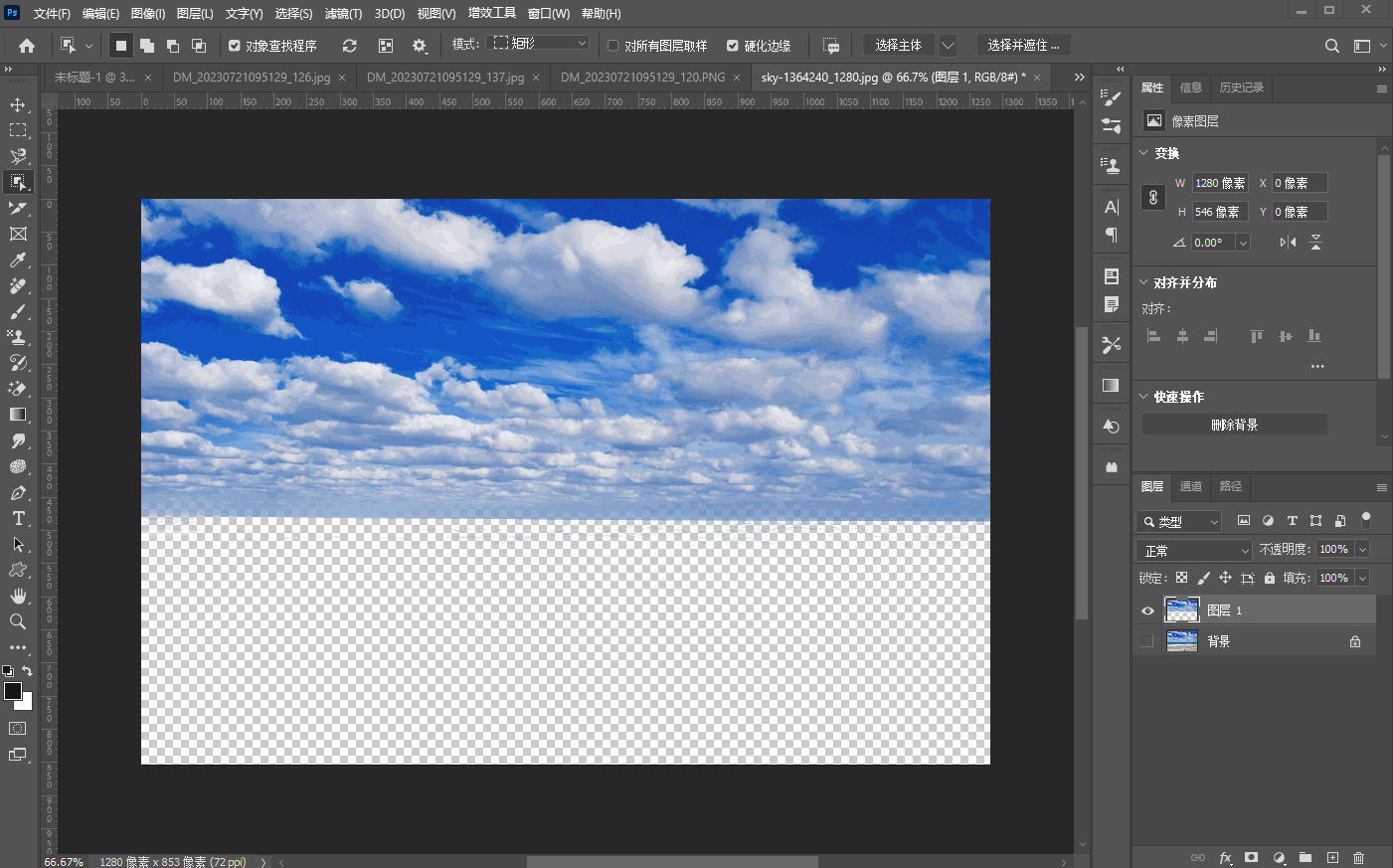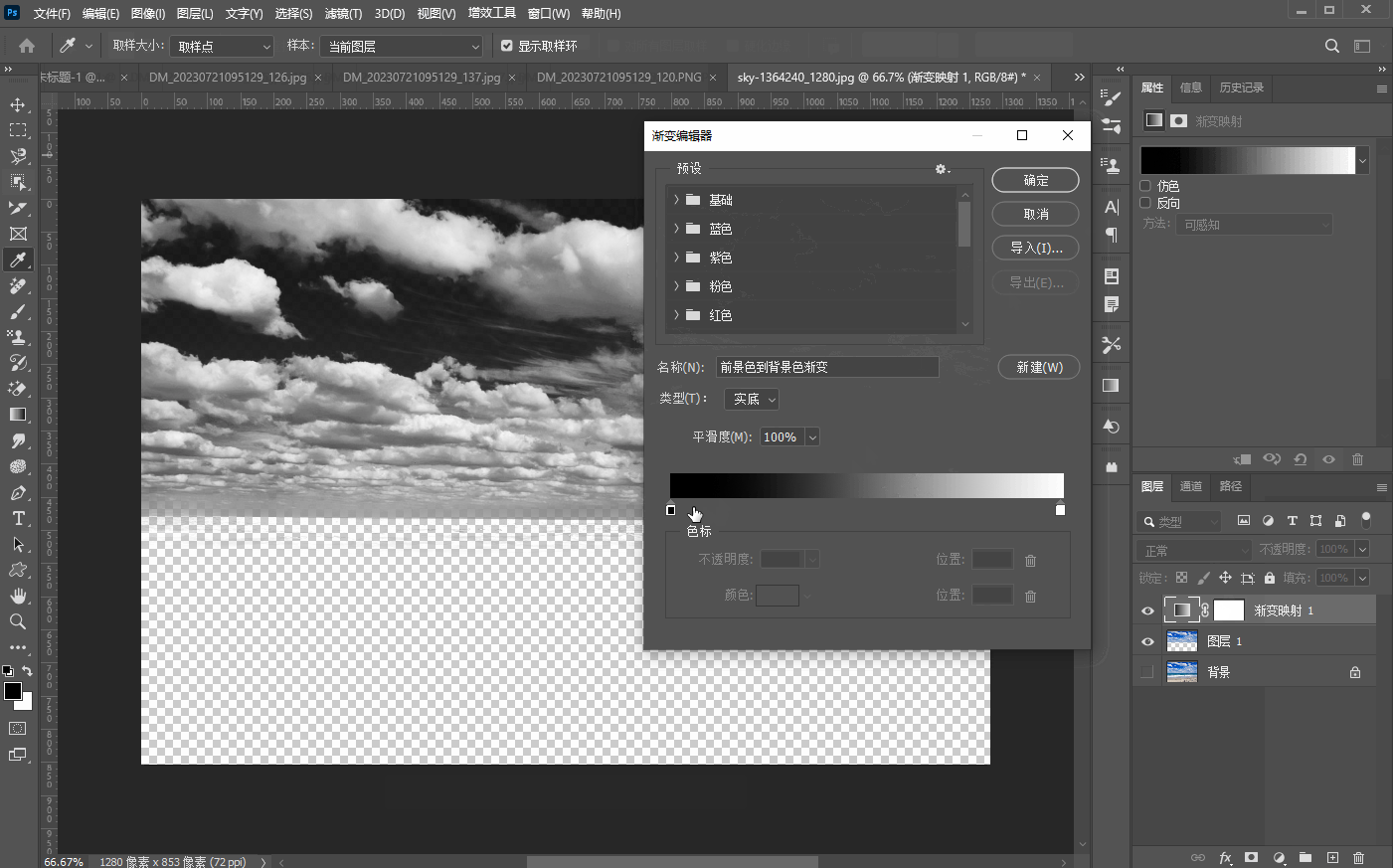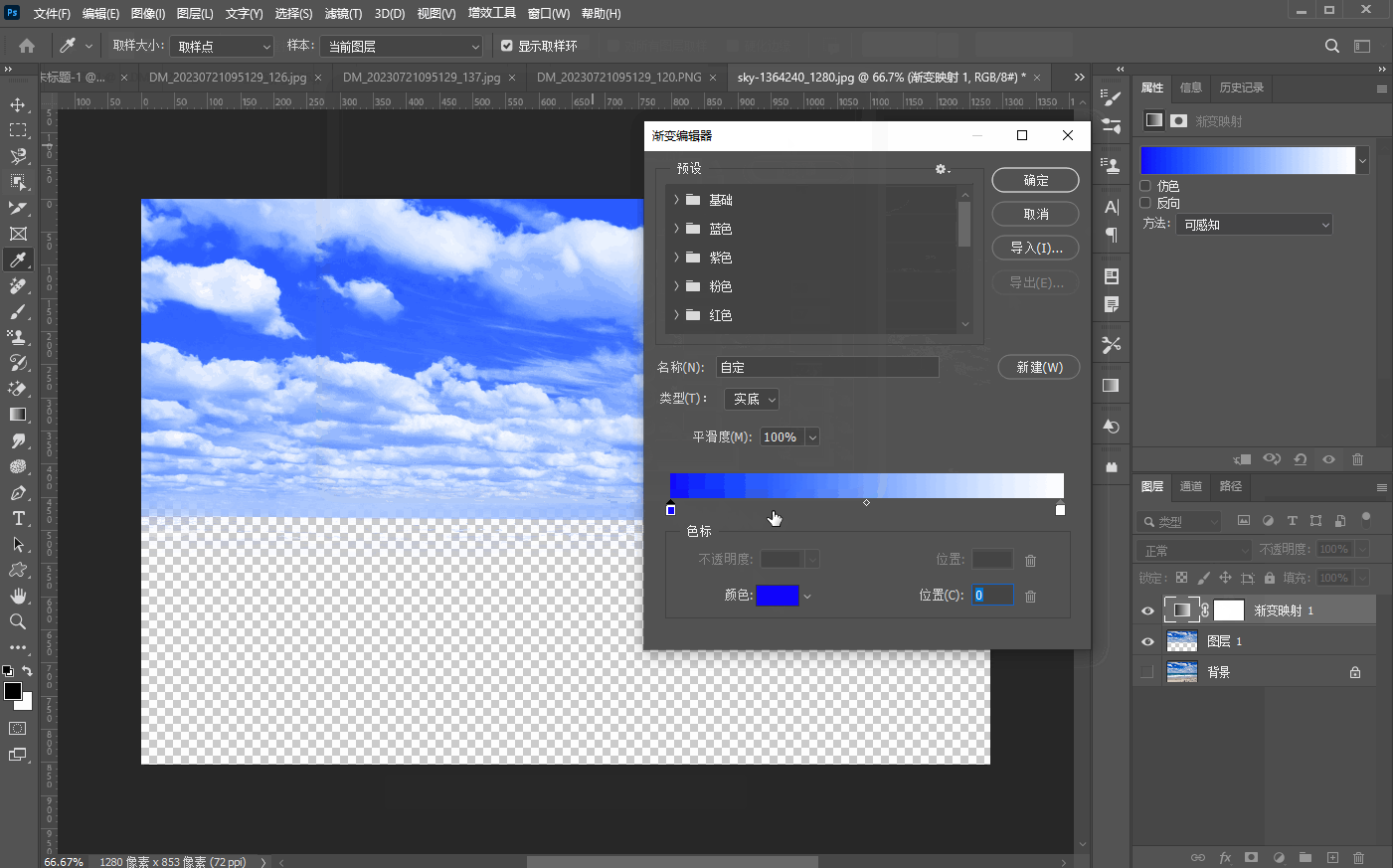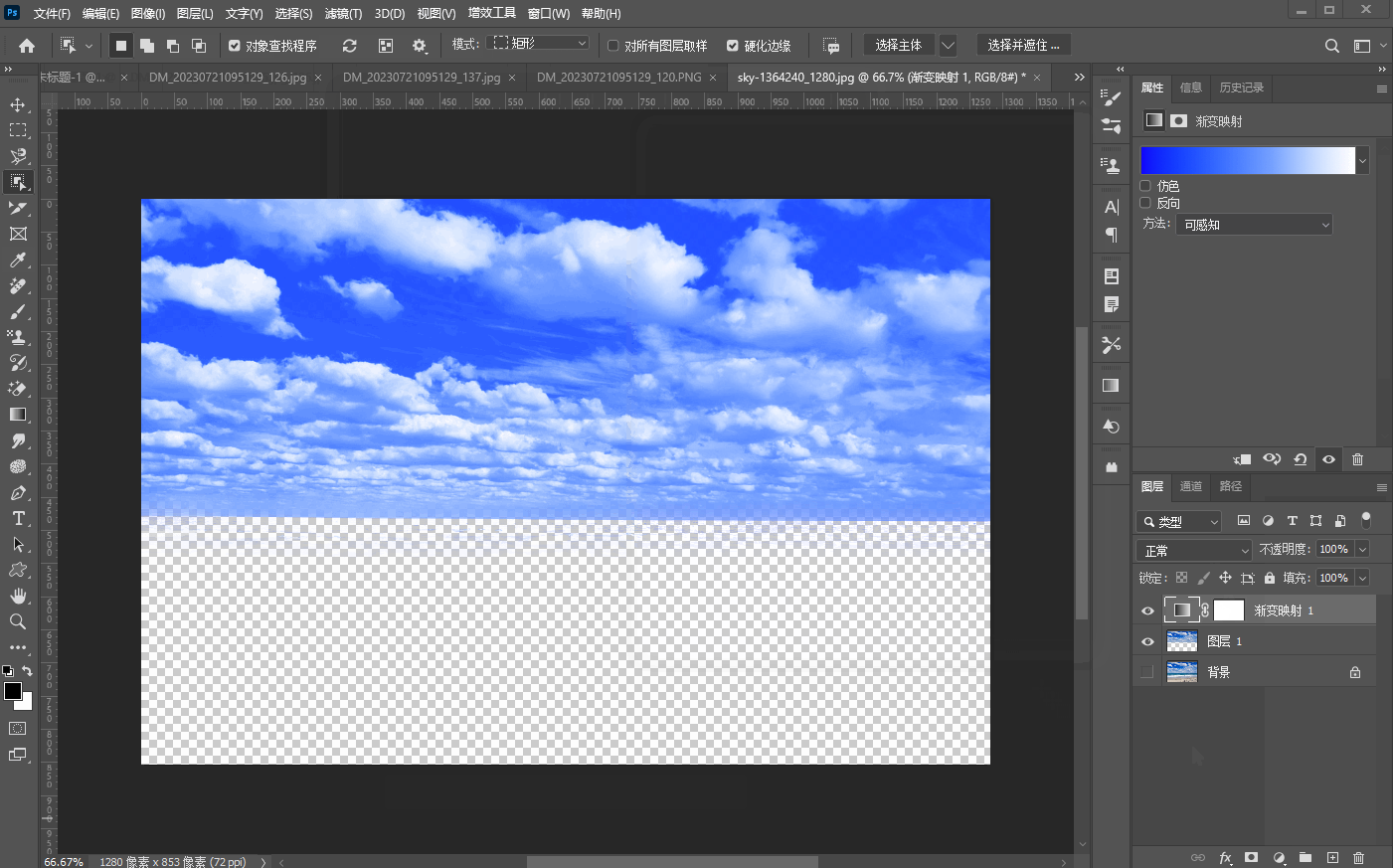
二十五、【色调调整基础】
文章目录 1、亮度/对比度a、亮度b、对比度 2、曝光度3、阈值4、色阶5、反相6、黑白7、渐变映射 1、亮度/对比度 a、亮度 亮度是指画面的明亮程度 b、对比度 对比度指的是一幅图像中,明暗区域最亮和最暗之间不同亮度层级的测量,如下图所示࿰…...
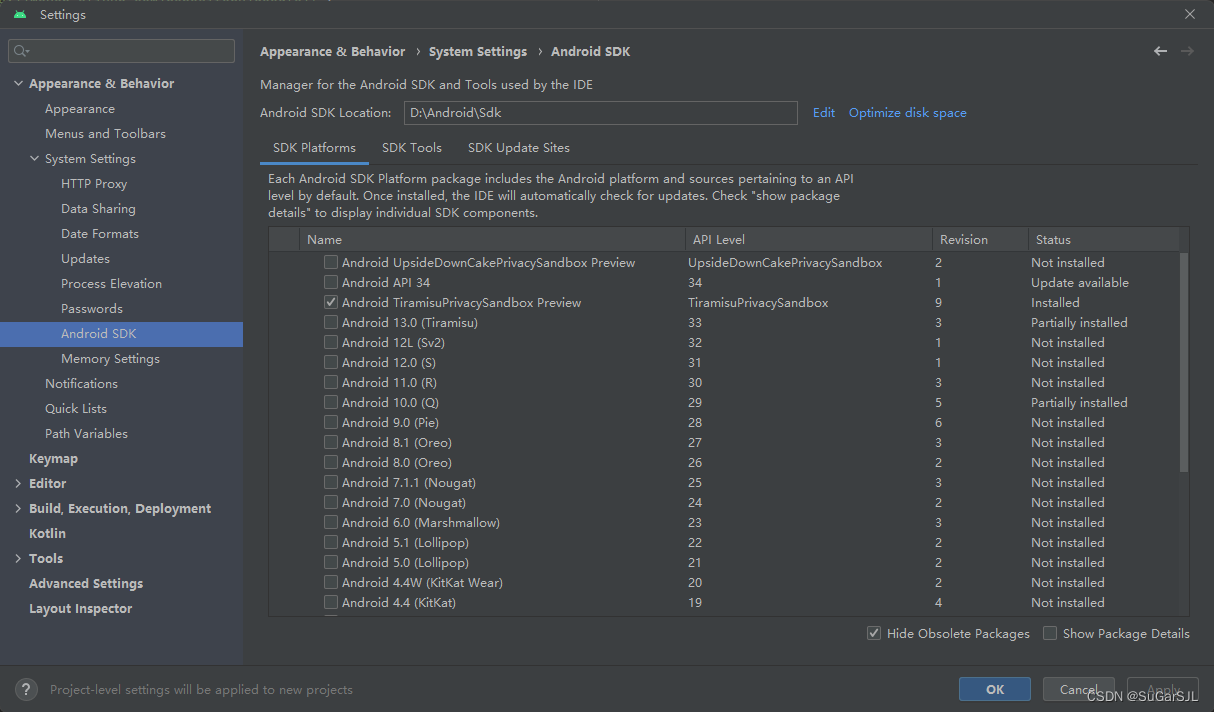
Android Studio SDK manager加载packages不全
打开Android Studio里的SDK manager,发现除了已安装的,其他的都不显示。 解决方法: 设置代理: 方便复制> http://mirrors.neusoft.edu.cn/ 重启Android Studio...

[esp32-wroom]基础开发
1、点亮LED灯 int led_pin2; void setup() {// put your setup code here, to run once:pinMode(led_pin,OUTPUT);}void loop() {// put your main code here, to run repeatedly:digitalWrite(led_pin,HIGH);delay(1000);digitalWrite(led_pin,LOW);delay(1000); } 2、LED流…...

利用Docker 实现 MiniOB环境搭建
官方文档有,但是感觉写的跟shift一样(或者是我的阅读理解跟shift一样 下面是自己的理解 一.下载docker 这个去官网下载安装,没什么说的 Docker: Accelerated Container Application Development 二.用docker下载MiniOB环境 1.打开powershell ( win r ,然后输入powershell…...

【DB2】—— 数据库表查询一直查不出来数据
问题描述 近日,数据库的测试环境中有一个打印日志表,一共有将近50w的数据,Java程序在查询的时候一直超时。 在DBvisualizer中查询数据无论是使用select * 还是 select count(*)查询的时候都是一直在执行,就是查询不到结果。 排查…...
【教程】使用vuepress构建静态文档网站,并部署到github上
官网 快速上手 | VuePress (vuejs.org) 构建项目 我们跟着官网的教程先构建一个demo 这里我把 vuepress-starter 这个项目名称换成了 howtolive 创建并进入一个新目录 mkdir howtolive && cd howtolive使用你喜欢的包管理器进行初始化 yarn init 这里的问题可以一…...

python 机器视觉 车牌识别 - opencv 深度学习 机器学习 计算机竞赛
1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 基于python 机器视觉 的车牌识别系统 🥇学长这里给一个题目综合评分(每项满分5分) 难度系数:3分工作量:3分创新点:3分 🧿 更多资…...
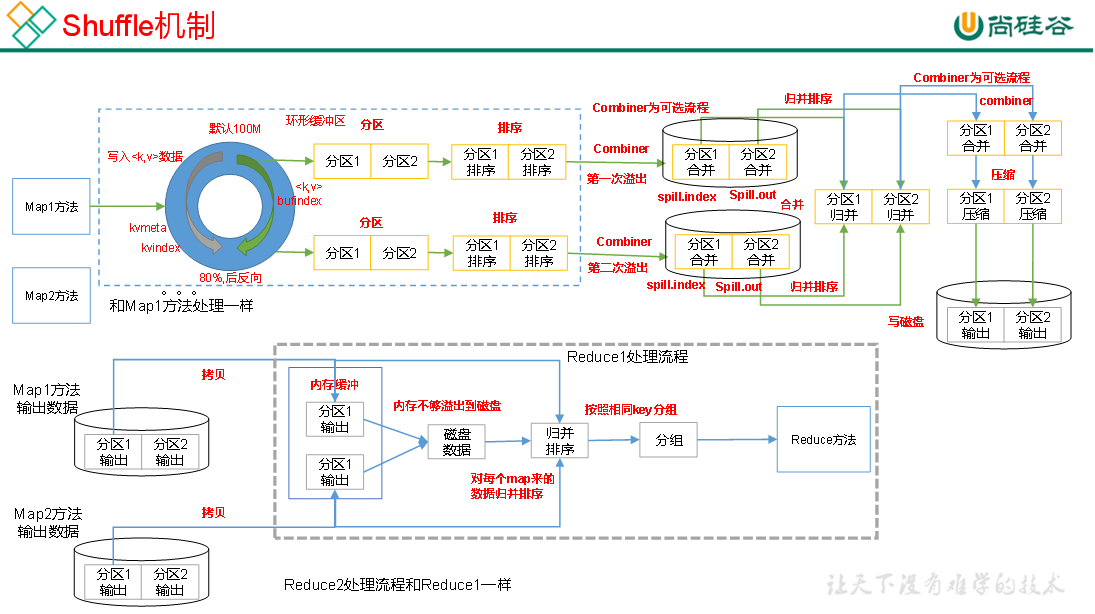
Hadoop3教程(十二):MapReduce中Shuffle机制的概述
文章目录 (95) Shuffle机制什么是shuffle?Map阶段Reduce阶段 参考文献 (95) Shuffle机制 面试的重点 什么是shuffle? Map方法之后,Reduce方法之前的这段数据处理过程,就叫做shuff…...

MySQL为什么用b+树
索引是一种数据结构,用于帮助我们在大量数据中快速定位到我们想要查找的数据。 索引最形象的比喻就是图书的目录了。注意这里的大量,数据量大了索引才显得有意义,如果我想要在[1,2,3,4]中找到4这个数据,直接对全数据检索也很快&am…...

浅谈机器学习中的概率模型
浅谈机器学习中的概率模型 其实,当牵扯到概率的时候,一切问题都会变的及其复杂,比如我们监督学习任务中,对于一个分类任务,我们经常是在解决这样一个问题,比如对于一个n维的样本 X [ x 1 , x 2 , . . . .…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

stm32wle5 lpuart DMA数据不接收
配置波特率9600时,需要使用外部低速晶振...
