List集合拆分为多个List
list 拆分
- 目录
- 概述
- 需求:
- 设计思路
- 实现思路分析
- 1.list 拆分是
- 2.用stream的parallel实现list的分批处理
- 3.使用stream的parallel实现list的分批处理
- 参考资料和推荐阅读
Survive by day and develop by night.
talk for import biz , show your perfect code,full busy,skip hardness,make a better result,wait for change,challenge Survive.
happy for hardess to solve denpendies.
目录

概述
list 拆分是一个常见的需求。
需求:
list 拆分是一个常见的需求。
设计思路
实现思路分析
1.list 拆分是
// 创建模拟listList<Integer> dataList = new ArrayList<>();for (int i = 1; i <= 22; i++) {dataList.add(i);}// 每批次数据记录数量int partialLimit = 10;//判断是否有必要分批if (partialLimit < dataList.size()) {//当前数据按限制条数可分为多少批次int part = dataList.size()/partialLimit;List<Integer> partList;for (int i = 0; i < part; i++) {// 截取批次长度的listpartList = dataList.subList(0, partialLimit);// 分批业务逻辑处理- 打印替代System.out.println("分割出口的数据: "+partList);// 去除已经处理的部分 (Arrays.asList()方式生成的数据不能进行此修改操作,会报错)partList.clear();System.out.println("剩余数据: "+dataList);}// 获取最后一次截取后的剩余列表数据if (!dataList.isEmpty()) {// 业务逻辑数据处理, - 打印替代System.out.println(dataList);}} else {System.out.println("数据不需要分批,直接进行业务逻辑处理!");}
2.用stream的parallel实现list的分批处理
// 按每5个一组分割int partialLimit = 5;List<Integer> list = Arrays.asList(1, 2, 3, 4, 5, 6, 7,8,9,10);// 获取需要分割的次数,注意不能直接除以批次数量int limit = (list.size()+partialLimit -1)/partialLimit;// 使用流遍历操作List<List<Integer>> arrayList = new ArrayList<>();Stream.iterate(0, n -> n + 1).limit(limit).forEach(i -> {arrayList.add(list.stream().skip((long) i * partialLimit).limit(partialLimit).collect(Collectors.toList()));});System.out.println(arrayList);
3.使用stream的parallel实现list的分批处理
// 按每5个一组分割int partialLimit = 5;List<Integer> list = Arrays.asList(1, 2, 3, 4, 5, 6, 7,8,9,10);// 获取需要分割的次数,注意不能直接除以批次数量,会丢失数据;int limit = (list.size()+partialLimit -1)/partialLimit;// 获取分割后的集合List<List<Integer>> splitList = Stream.iterate(0, n -> n + 1).limit(limit).parallel().map(a -> list.stream().skip((long) a * partialLimit).limit(partialLimit).parallel().collect(Collectors.toList())).collect(Collectors.toList());// 执行具体业务方法。打印代替System.out.println(splitList);
参考资料和推荐阅读
参考资料
官方文档
开源社区
博客文章
书籍推荐
1.https://www.cnblogs.com/ChenQ2/p/16636306.html
2.https://www.cnblogs.com/ChenQ2/p/16636306.html
欢迎阅读,各位老铁,如果对你有帮助,点个赞加个关注呗!同时,期望各位大佬的批评指正~
相关文章:

List集合拆分为多个List
list 拆分 目录概述需求: 设计思路实现思路分析1.list 拆分是2.用stream的parallel实现list的分批处理3.使用stream的parallel实现list的分批处理 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full bus…...
:MapReduce中的分区)
Hadoop3教程(十三):MapReduce中的分区
文章目录 (96) 默认HashPartitioner分区(97) 自定义分区案例(98)分区数与Reduce个数的总结参考文献 (96) 默认HashPartitioner分区 分区,是Shuffle里核心的一环…...
笔记本Win10系统一键重装操作方法
笔记本电脑已经成为大家日常生活和工作中必不可少的工具之一,如果笔记本电脑系统出现问题了,那么就会影响到大家的正常操作。这时候就可以考虑给笔记本电脑重装系统了。接下来小编给大家介绍关于一键重装Win10笔记本电脑系统的详细步骤方法。 推荐下载 系…...

FilterRegistrationBean能不能排除指定url
文章目录 什么是FilterRegistrationBean举个栗子但是如果我想要排除某些uri方法总结FilterRegistrationBean只能设置指定的url进行过滤,而不能指定排除uri,只能使用OncePerRequestFilter的shouldNotFilter方法,排除uri 什么是FilterRegistrationBean FilterRegistrationBean是…...
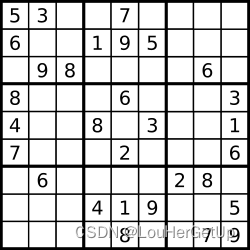
【LeetCode】36. 有效的数独
1 问题 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图&…...
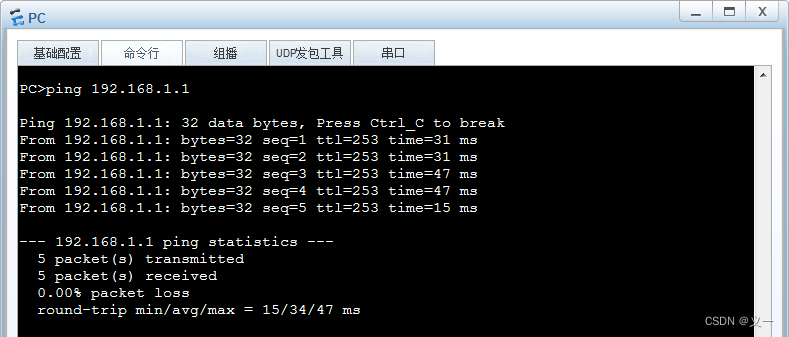
华为---PPP协议简介及示例配置
PPP协议简介 PPP是Point-to-Point Protocol的简称,中文翻译为点到点协议。与以太网协议一样,PPP也是一个数据链路层协议。以太网协议定义了以太帧的格式,PPP协议也定义了自己的帧格式,这种格式的帧称为PPP帧。 利用PPP协议建立的二层网络称为…...
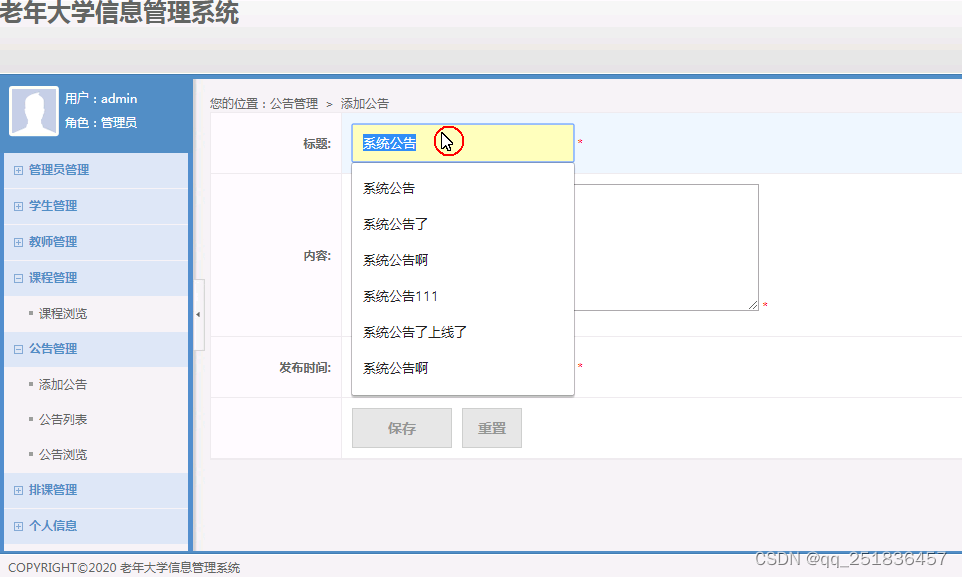
asp.net老年大学信息VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio计算机毕业设计
一、源码特点 asp.net老年大学信息管理系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c# 语言开发 asp.net老年大学信息管理系统…...
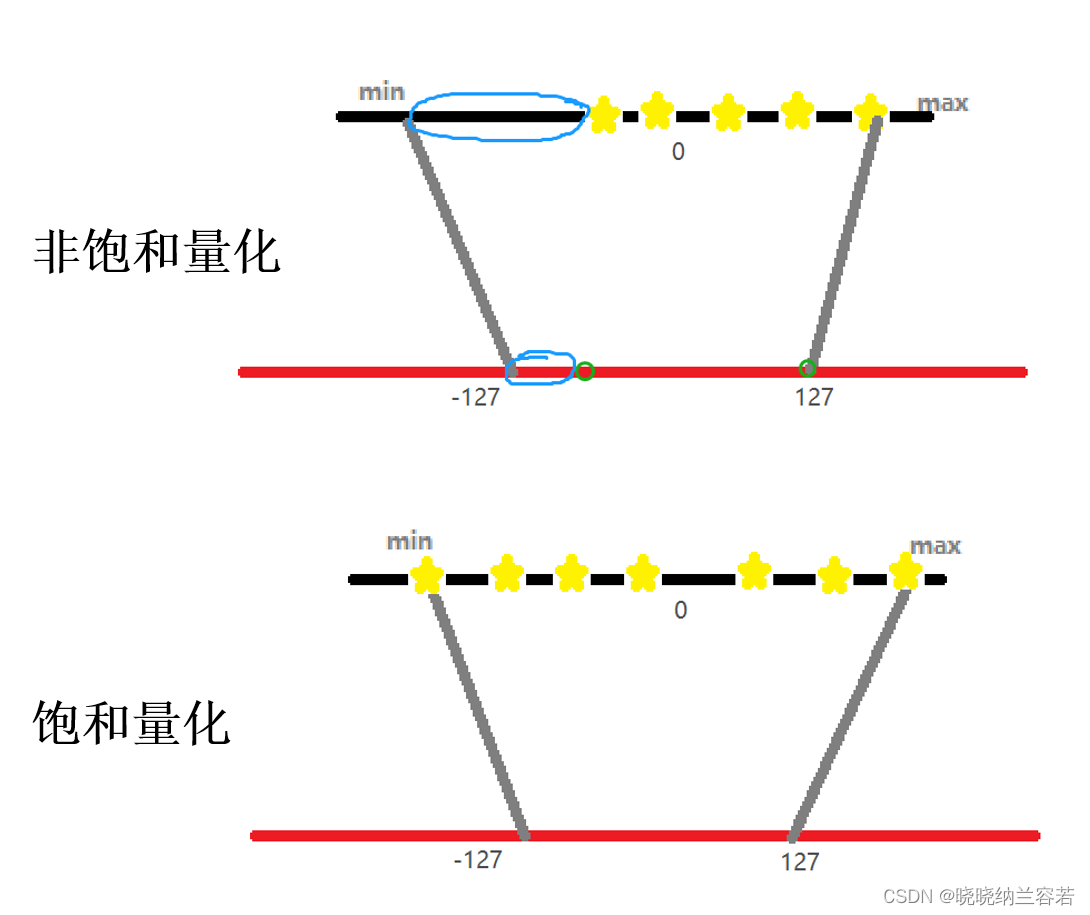
模型量化笔记--对称量化和非对称量化
1–量化映射 量化映射的通用公式为: r S ( q − Z ) r S(q - Z) rS(q−Z) 其中r表示量化前数据的真实值,S表示缩放因子,q表示量化后的数值,Z表示零点 2–非对称量化 非对称量化需要一个偏移量Z来完成零点的映射,即量化前的零…...

PA2019 Terytoria
洛谷P5987 [PA2019] Terytoria 题目大意 在一个平面直角坐标系上,有一个长度为 X X X,宽度为 Y Y Y的地图,这个地图的左边界和右边界是连通的,下边界和上边界也是连通的。 在地图中,有 X Y X\times Y XY个格子以及…...

内容分发网络CDN分布式部署真的可以加速吗?原理是什么?
Cdn快不快?她为什么会快?同样的带宽为什么她会快?原理究竟是什么,同学们本着普及知识的想法,我了解的不是很深入,适合小白来看我的帖子,如果您是大佬还请您指正错误的地方,先谢谢大佬…...
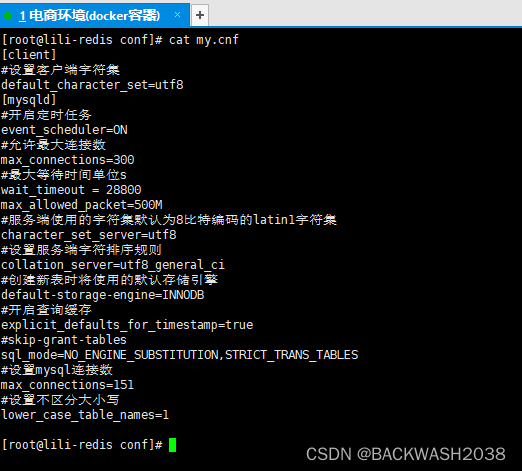
微服务docker部署实战
docker基础和进阶(*已掌握的可以跳过 *) 基础 docker基础 进阶 docker进阶 准备工作 提前准备好mysql和redis的配置,如下 在/zzq/mysql/conf目录下配置mysql配置文件my.cnf [client] #设置客户端字符集 default_character_setutf8 [mysqld] #开启定时任务 event_s…...

js实现拖拽功能
基于onMouseDown 、onMouseMove 、onMouseUp 使用 mousedown、mousemove 和 mouseup 事件来实现拖拽的基本思路是: 在 mousedown 事件中,开始追踪拖拽操作并记录鼠标按下的位置。 在 mousemove 事件中,根据鼠标的移动,更新被拖拽…...

数据库主从切换过程中Druid没法获取连接错误
背景: 今天dba在进行DB的主从切换,导致应用一直报错,获取不到DB连接,druid的错误信息如下: Could not open JDBC Connection for transaction; nested exception is com.alibaba.druid.pool.GetConnectionTimeoutExc…...
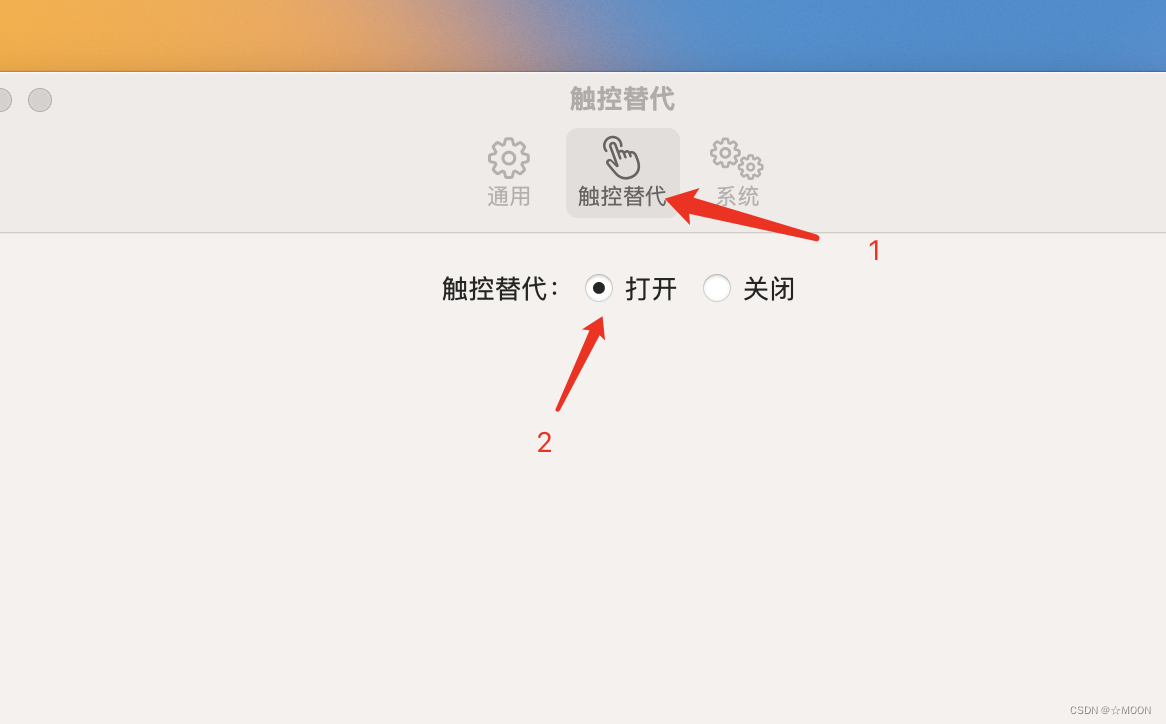
【iOS】Mac M1安装iPhone及iPad的app时设置问题
【iOS】Mac M1安装iPhone及iPad的app时设置问题 简介一,设置问题二,适配问题 简介 由于 苹果M1芯片的Mac可用安装iPhone以及iPad应用,因为开发者并没有适配Mac,因此产生了很多奇怪问题,这里总结归纳Mac M1安装iPhone和…...
Springboot 启动报错@spring.active@解析错误
Caused by: org.yaml.snakeyaml.scanner.ScannerException: while scanning for the next token found character that cannot start any token. (Do not use for indentation)in reader, line 10, column 13:active: spring.active^查看是否勾选...

【算法挨揍日记】day15——560. 和为 K 的子数组、974. 和可被 K 整除的子数组
560. 和为 K 的子数组 560. 和为 K 的子数组 题目描述: 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 子数组是数组中元素的连续非空序列。 解题思路: 我们可以很容易想到暴力解法…...

数字时代的探索与革新:Socks5代理的引领作用
在当今快速发展的数字时代,技术创新推动着社会的变革与进步。Socks5代理作为一项重要的网络技术,正引领着跨界电商、爬虫数据分析、企业全球化和游戏体验优化等领域的发展。本文将深入探讨Socks5代理技术在这些领域中的引领作用,以及它如何塑…...
算法-堆/归并排序-排序链表
算法-堆/归并排序-排序链表 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/sort-list/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 优先级队列构建大顶堆 2.1 思路 优先级队列构建小顶堆链表所有元素放入小顶堆依次取出堆顶…...
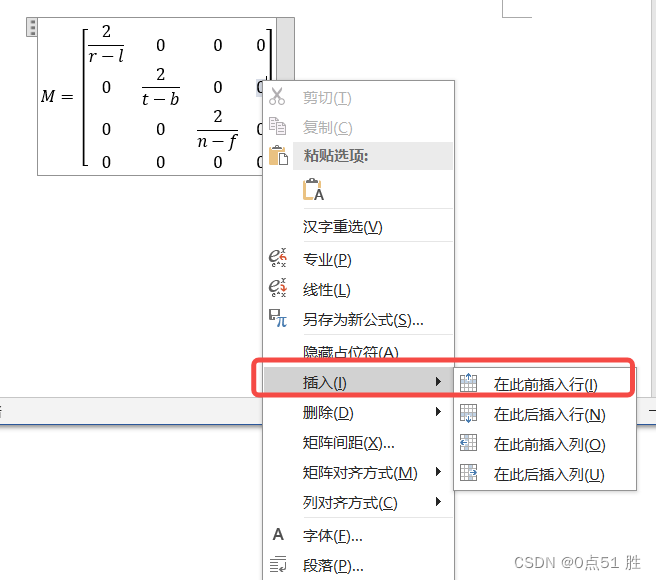
word 如何编写4x4矩阵
百度上给的教程,打印出来没有对齐 https://jingyan.baidu.com/article/6b182309995f8dba58e159fc.html 百度上的方式试了一下,不会对齐。导致公式看起来很奇怪。 下面方式会自动对齐 摸索了一下发现可以用下面这种方式编写 4x4 矩阵。先创建一个 3x3…...
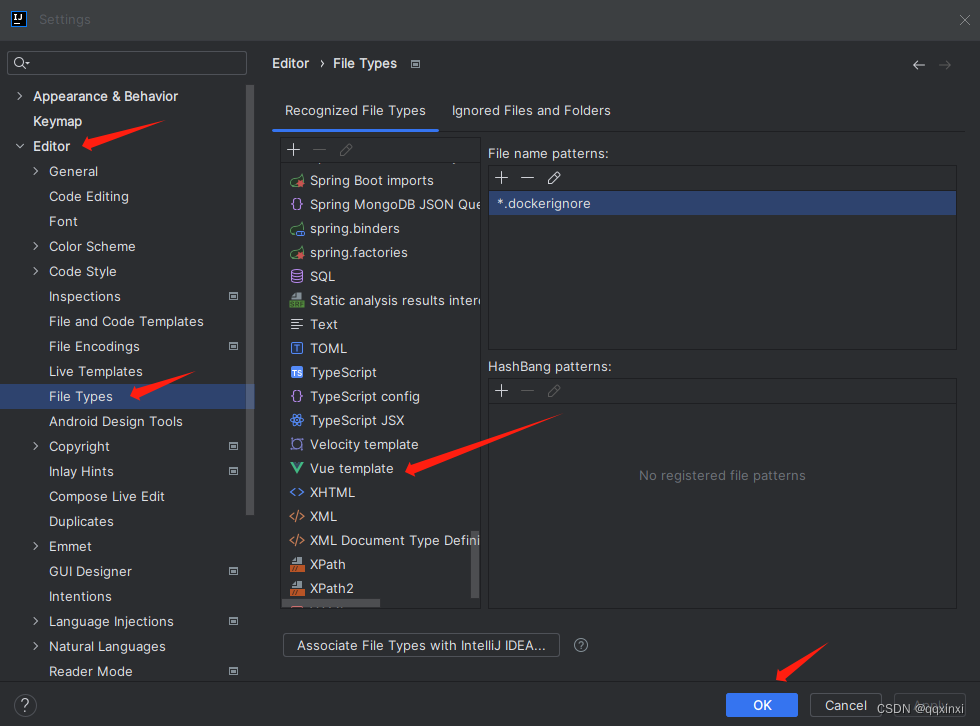
INTELlij IDEA编辑VUE项目
菜单中选择setting–>Plugins 或者快捷键 ctrlalts 搜索vue,但有些情况会搜索不出来,先说搜索到的情况 如下图所示: 如果没有vue.js则说明过去已经安装了。 搜索到了后点击Install安装即可, 但即使搜索成功了,也不…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
