多数元素[简单]
优质博文:IT-BLOG-CN
一、题目
给定一个大小为n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数大于n/2的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109
进阶: 尝试设计时间复杂度为O(n)、空间复杂度为O(1)的算法解决此问题。
二、代码
【1】哈希映射(HashMap): 来存储每个元素以及出现的次数。对于哈希映射中的每个键值对,键表示一个元素,值表示该元素出现的次数。我们用一个循环遍历数组nums并将数组中的每个元素加入哈希映射中。在这之后,我们遍历哈希映射中的所有键值对,返回值最大的键。我们同样也可以在遍历数组nums时候使用打擂台的方法,维护最大的值,这样省去了最后对哈希映射的遍历。
class Solution {public int majorityElement(int[] nums) {// 思想: 通过 hashMap 存放 value 和 count , 如果 count > n/2 直接返回if (nums.length == 0) {return 0;}int mid = nums.length/2;Map<Integer, Integer> map = new HashMap<Integer, Integer>(); for (int i = 0; i < nums.length; i++) {map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);if (map.getOrDefault(nums[i], 0) > mid) {return nums[i];}}return 0;}
}
时间复杂度: O(n)其中n是数组nums的长度。我们遍历数组nums一次,对于nums中的每一个元素,将其插入哈希表都只需要常数时间。如果在遍历时没有维护最大值,在遍历结束后还需要对哈希表进行遍历,因为哈希表中占用的空间为O(n)(可参考下文的空间复杂度分析),那么遍历的时间不会超过O(n)。因此总时间复杂度为O(n)。
空间复杂度: O(n)哈希表最多包含n−⌊n/2⌋个键值对,所以占用的空间为O(n)。这是因为任意一个长度为n的数组最多只能包含n个不同的值,但题中保证nums一定有一个众数,会占用(最少)⌊n/2⌋+1个数字。因此最多有n−(⌊n/2⌋+1)个不同的其他数字,所以最多有n−⌊n/2⌋个不同的元素。
【2】排序: 如果将数组nums中的所有元素按照单调递增或单调递减的顺序排序,那么下标为⌊n/2⌋的元素(下标从0开始)一定是众数。
class Solution {public int majorityElement(int[] nums) {Arrays.sort(nums);return (nums[nums.length/2]);}
}
时间复杂度: O(nlogn)将数组排序的时间复杂度为O(nlogn)。
空间复杂度: O(logn)如果使用语言自带的排序算法,需要使用O(logn)的栈空间。如果自己编写堆排序,则只需要使用O(1)的额外空间。
【3】Boyer-Moore 投票算法: 如果我们把众数记为+1,把其他数记为−1,将它们全部加起来,显然和大于0,从结果本身我们可以看出众数比其他数多。
oyer-Moore算法的本质和分治十分类似。我们首先给出Boyer-Moore算法的详细步骤:
【1】我们维护一个候选众数candidate和它出现的次数count。初始时candidate可以为任意值,count为0;
【1】我们遍历数组nums中的所有元素,对于每个元素x,在判断x之前,如果count的值为0,我们先将x的值赋予candidate,随后我们判断x:如果x与candidate相等,那么计数器count的值增加1;如果x与candidate不等,那么计数器count的值减少1。在遍历完成后,candidate即为整个数组的众数。
我们举一个具体的例子,例如下面的这个数组:
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
在遍历到数组中的第一个元素以及每个在 | 之后的元素时,candidate都会因为count的值变为0而发生改变。最后一次candidate的值从5变为7,也就是这个数组中的众数。
Boyer-Moore算法的正确性较难证明,这里给出一种较为详细的用例子辅助证明的思路,供读者参考:首先我们根据算法步骤中对count的定义,可以发现:在对整个数组进行遍历的过程中,count的值一定非负。这是因为如果count的值为0,那么在这一轮遍历的开始时刻,我们会将x的值赋予candidate并在接下来的一步中将count的值增加1。因此count的值在遍历的过程中一直保持非负。
那么count本身除了计数器之外,还有什么更深层次的意义呢?我们还是以数组
[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
作为例子,首先写下它在每一步遍历时candidate和count的值:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
candidate: 7 7 7 7 7 7 5 5 5 5 5 5 7 7 7 7
count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
我们再定义一个变量value,它和真正的众数maj绑定。在每一步遍历时,如果当前的数x和maj相等,那么value的值加1,否则减1。value的实际意义即为:到当前的这一步遍历为止,众数出现的次数比非众数多出了多少次。我们将value的值也写在下方:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
value: 1 2 1 2 1 0 -1 0 -1 -2 -1 0 1 2 3 4
有没有发现什么?我们将count和value放在一起:
nums: [7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]
count: 1 2 1 2 1 0 1 0 1 2 1 0 1 2 3 4
value: 1 2 1 2 1 0 -1 0 -1 -2 -1 0 1 2 3 4
发现在每一步遍历中,count和value要么相等,要么互为相反数!并且在候选众数candidate就是maj时,它们相等,candidate是其它的数时,它们互为相反数!
为什么会有这么奇妙的性质呢?这并不难证明:我们将候选众数candidate保持不变的连续的遍历称为「一段」。在同一段中,count的值是根据candidate == x的判断进行加减的。那么如果candidate恰好为maj,那么在这一段中,count和value的变化是同步的;如果candidate不为maj,那么在这一段中count和value的变化是相反的。因此就有了这样一个奇妙的性质。
这样以来,由于:我们证明了count的值一直为非负,在最后一步遍历结束后也是如此;由于value的值与真正的众数maj绑定,并且它表示「众数出现的次数比非众数多出了多少次」,那么在最后一步遍历结束后,value的值为正数;
在最后一步遍历结束后,count非负,value为正数,所以它们不可能互为相反数,只可能相等,即count == value。因此在最后「一段」中,count的value的变化是同步的,也就是说,candidate中存储的候选众数就是真正的众数maj。
class Solution {public int majorityElement(int[] nums) {int count = 0;Integer candidate = null;for (int num : nums) {if (count == 0) {candidate = num;}count += (num == candidate) ? 1 : -1;}return candidate;}
}
时间复杂度: O(n),Boyer-Moore算法只对数组进行了一次遍历。
空间复杂度: O(1),Boyer-Moore算法只需要常数级别的额外空间。
相关文章:

多数元素[简单]
优质博文:IT-BLOG-CN 一、题目 给定一个大小为n的数组nums,返回其中的多数元素。多数元素是指在数组中出现次数大于n/2的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。 示例 1: 输入:nums [3,2,3…...

34 个高质量免费教育资源
🧑🎓 综合型在线学习网站:21个 🛜 专业类在线教育网站:13个 ⬇️⬇️⬇️ 0 examtopics www.examtopics.cn 专业的AWS等IT认证考试题库 一、综合型在线学习网站 1、Coursera coursera.org 美国斯坦福大学两名计算机…...
基础课5——语音合成技术
TTS是语音合成技术的简称,也称为文语转换或语音到文本。它是指将文本转换为语音信号,并通过语音合成器生成可听的语音。TTS技术可以用于多种应用,例如智能语音助手、语音邮件、语音新闻、有声读物等。 TTS技术通常包括以下步骤: …...

安全事件报告和处置制度
1、总则 1.1、目的 为了严密规范XXXXX单位信息系统的安全事件处理程序,确保各业务系统的正常运行和系统及网络的安全事件得到及时响应、处理和跟进,保障网络和系统持续安全运行,确保XXXXX单位重要计算机信息系统的实体安全、运行安全和数据…...

java干掉 if-else
前言 传统做法-if-else分支 策略模式Map字典 责任链模式 策略模式注解 物流行业中,通常会涉及到EDI报文(XML格式文件)传输和回执接收,每发送一份EDI报文,后续都会收到与之关联的回执(标识该数据在第三方系统中的流转状态ÿ…...

29 Python的pandas模块
概述 在上一节,我们介绍了Python的numpy模块,包括:多维数组、数组索引、数组操作、数学函数、线性代数、随机数生成等内容。在这一节,我们将介绍Python的pandas模块。pandas模块是Python编程语言中用于数据处理和分析的强大模块&a…...
树叶识别系统python+Django网页界面+TensorFlow+算法模型+数据集+图像识别分类
一、介绍 树叶识别系统。使用Python作为主要编程语言开发,通过收集常见的6中树叶(‘广玉兰’, ‘杜鹃’, ‘梧桐’, ‘樟叶’, ‘芭蕉’, ‘银杏’)图片作为数据集,然后使用TensorFlow搭建ResNet50算法网络模型,通过对…...

【问题解决:配置】解决spring mvc项目 get请求 获取中文字符串参数 乱码
get类型请求的发送过程 前端发送一个get请求的过程: 封装参数进行URL编码,也就是将中文编码成一个带有百分号的字符串,具体可以在这个网站进行测试。http://www.esjson.com/urlEncode.html 进行Http编码,这里浏览器或者postman都…...

python每日一练(9)
🌈write in front🌈 🧸大家好,我是Aileen🧸.希望你看完之后,能对你有所帮助,不足请指正!共同学习交流. 🆔本文由Aileen_0v0🧸 原创 CSDN首发🐒 如…...

JVM第十四讲:调试排错 - Java 内存分析之堆内存和MetaSpace内存
调试排错 - Java 内存分析之堆内存和MetaSpace内存 本文是JVM第十四讲,以两个简单的例子(堆内存溢出和MetaSpace (元数据) 内存溢出)解释Java 内存溢出的分析过程。 文章目录 调试排错 - Java 内存分析之堆内存和MetaSpace内存1、常见的内存溢出问题(内存…...

【1day】泛微e-office OA SQL注入漏洞学习
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现...

线上问题:所有用户页面无法打开
线上问题:所有用户页面无法打开 1 线上问题2 问题处理3 复盘3.1 第二天观察 1 线上问题 上午进入工作时间,Cat告警出现大量linda接口超时Exception。 随后,产品和运营反馈无法打开页面,前线用户大量反馈无法打开页面。 2 问题处…...

RabbitMQ和spring boot整合及其他内容
在现代分布式应用程序的设计中,消息队列系统是不可或缺的一部分,它为我们提供了解耦组件、实现异步通信和确保高性能的手段。RabbitMQ,作为一款强大的消息代理,能够协助我们实现这些目标。在本篇CSDN博客中,我们将探讨…...
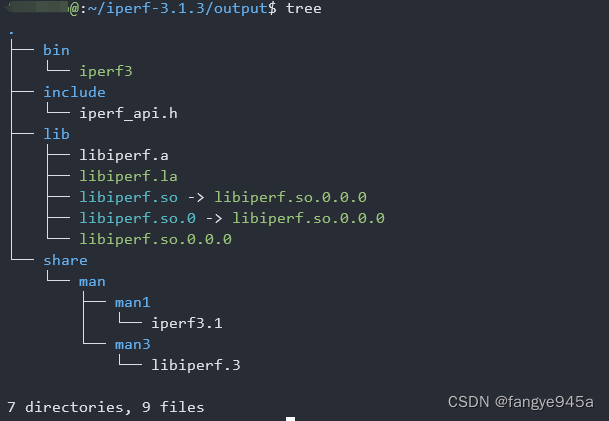
iperf3交叉编译
简介 iperf3是一个用于执行网络吞吐量测量的命令行工具。它支持时序、缓冲区、协议(TCP,UDP,SCTP与IPv4和IPv6)有关的各种参数。对于每次测试,它都会详细的带宽报告,延迟抖动和数据包丢失。 如果是ubuntu系…...
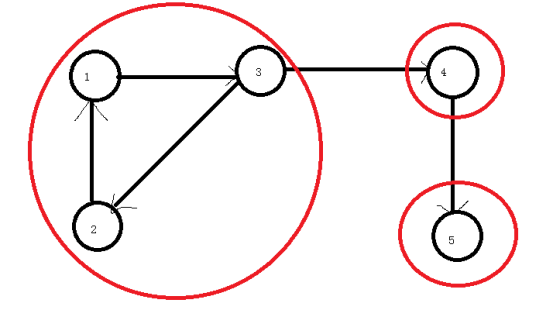
TARJAN复习 求强连通分量、割点、桥
TARJAN复习 求强连通分量、割点、桥 文章目录 TARJAN复习 求强连通分量、割点、桥强连通分量缩点桥割点 感觉之前写的不好, 再水一篇博客 强连通分量 “有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有…...

python实现批量数据库数据插入
import pandas as pd import pymysql # 连接 MySQL 数据库 conn pymysql.connect( hostlocalhost, useryour_username, passwordyour_password, databaseyour_database_name, charsetutf8mb4, ) # 读取已有数据 existing_data pd.read_csv("86w全…...

python安装,并搞定环境配置和虚拟环境
鄙人使用Python来进行项目的开发,一般都是通过Anaconda来完成的。Anaconda不但封装了Python,还包含了创建虚拟环境的工具。 anaconda安装 安装anaconda,可以搜索清华镜像源,然后搜索anaconda,点击进入,然…...
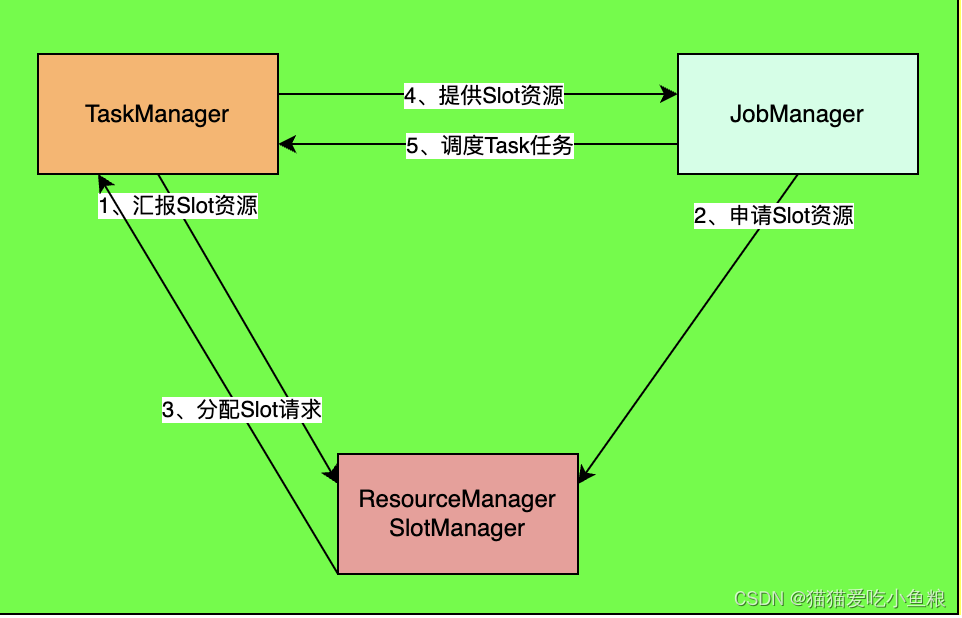
Flink 的集群资源管理
集群资源管理 一、ResourceManager 概述 1、ResourceManager 作为统一的集群资源管理器,用于管理整个集群的计算资源,包括 CPU资源、内存资源等。 2、ResourceManager 负责向集群资源管理器申请容器资源启动TaskManager实例,并对TaskManag…...

STM32学习笔记
前言 今天开始学习STM32,公司封闭git网络,所以选择CSDN来同步学习进度,方便公司和家里都能更新学习笔记。 参考学习资料 江科大STM32教学视频: 江科大自动协STM32视频_哔哩哔哩_bilibili...
Java应用性能问题诊断技巧
作者:张彦东 参考:https://developer.aliyun.com/ebook/450?spma2c6h.20345107.ebook-index.28.6eb21f54J7SUYc 文章目录 (一)内存1.内存2.内存-JMX3.内存-Jmap4.内存-结合代码确认问题 (二)CPU1.CPU-JMX或…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
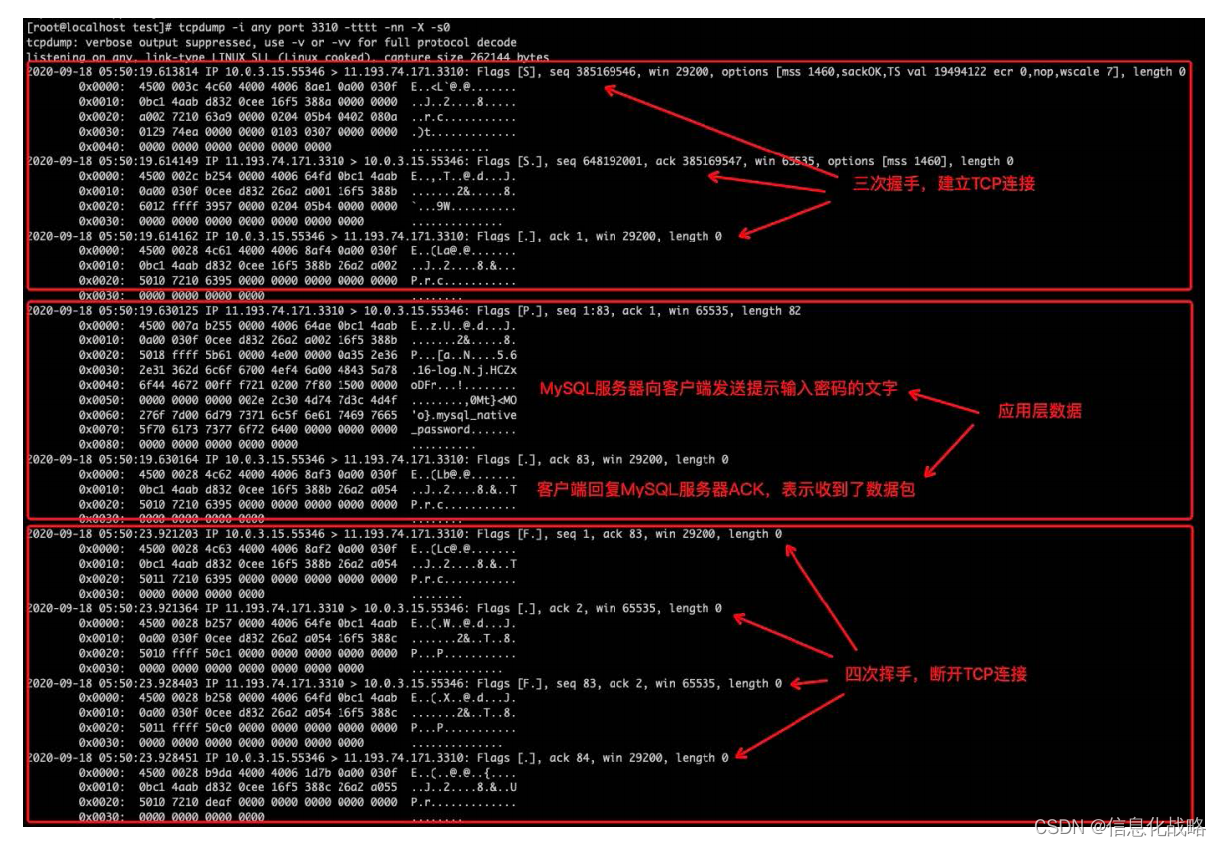
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
