【Hello Algorithm】暴力递归到动态规划(三)
暴力递归到动态规划(三)
- 最长公共子序列
- 递归版本
- 动态规划
- 最长回文串子序列
- 方法一
- 方法二
- 递归版本
- 动态规划
- 象棋问题
- 递归版本
- 动态规划
- 咖啡机问题
- 递归版本
- 动态规划
最长公共子序列
这是leetcode上的一道原题 题目连接如下
最长公共子序列
题目描述如下
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
递归版本
还是一样 我们首先来设计一个函数 函数原型如下
int process(string& str1 , string& str2 , int i , int j)
这个递归函数的含义是 给你两个字符串 s1 和 s2 再给你它们的一个最大下标 现在要求这个函数返回它们公共子序列的最大值
参数表示如下
- int i : 表示一个字符串str1中的下标
- int j : 表示一个字符串str2中的下标
还是一样 我们首先想base case
- 假如i的下标为0 j的下标也为0 此时我们就可以直接返回一个确定的值
代码表示如下
// base case if (i == 0 && j == 0) { return str1[i] == str2[j] ? 1 : 0; }
此时我们排除了i 和 j都为0的情况 剩下了三种情况
- i j 其中一个为0 (两种)
- i j都不为0
当i j都不为0时候 我们还要讨论 i j 是否为公共子序列的下标也是分为三种情况
- i可能是 j不是
- j可能是 i不是
- i j都是
之后我们分别将代码全部写好就可以了
if (i == 0){if (str1[i] == str2[j]){return 1;}else {return process(str1 , str2 , i , j-1);}}else if (j == 0){if (str1[i] == str2[j]){return 1;}else { return process(str1 , str2 , i - 1 , j); }}else {// j != 0;// i != 0;// possible i ... jint p1 = process(str1 , str2 , i - 1 , j);int p2 = process(str1 , str2 , i , j - 1);int p3 = str1[i] == str2[j] ? 1 + process(str1 , str2 , i -1 , j -1) : 0 ;return max(p1 , max (p2 , p3));}
}动态规划
我们观察原递归函数
process(string& str1 , string& str2 , int i , int j)
我们发现变化的值只有 i 和 j
于是我们可以利用i j 做出一张dp表
还是一样 我们首先来看base case
// base case if (i == 0 && j == 0) { return str1[i] == str2[j] ? 1 : 0; }
于是我们就可以把i == 0 并且 j ==0 的这些位置值填好
dp[0][0] = str1[0] == str2[0] ? 1 : 0;
之后根据 i == 0 j ==0 这两个分支继续动规
for (int j = 1 ; j < static_cast<int>(str2.size()) ; j++){ dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j-1]; } for (int i = 1 ; i < static_cast<int>(str1.size()) ; i++){ dp[i][0] = str1[i] == str2[0] ? 1 : dp[i-1][0];}
递归的最后一部分依赖三个位置
else {// j != 0;// i != 0;// possible i ... jint p1 = process(str1 , str2 , i - 1 , j);int p2 = process(str1 , str2 , i , j - 1);int p3 = str1[i] == str2[j] ? 1 + process(str1 , str2 , i -1 , j -1) : 0 ;return max(p1 , max (p2 , p3));}
我们只需要再递归表中依次填写即可 代码表示如下
int process1(string& str1, string& str2, vector<vector<int>>& dp)
{ dp[0][0] = str1[0] == str2[0] ? 1 : 0; for (int j = 1 ; j < static_cast<int>(str2.size()) ; j++) { dp[0][j] = str1[0] == str2[j] ? 1 : dp[0][j-1]; } for (int i = 1 ; i < static_cast<int>(str1.size()) ; i++) { dp[i][0] = str1[i] == str2[0] ? 1 : dp[i-1][0]; } for (int i = 1 ; i < static_cast<int>(str1.size()) ; i++) { for (int j = 1 ; j < static_cast<int>(str2.size()) ; j++) { int p1 = dp[i-1][j]; int p2 = dp[i][j-1]; int p3 = str1[i] == str2[j] ? 1 + dp[i-1][j-1] : 0; dp[i][j] = max(p1 , max(p2 , p3)); } } return dp[str1.size() - 1][str2.size() - 1];
}
最长回文串子序列
方法一
做这道题目我们其实可以复用下上面的最长公共子序列的代码来做
我们可以将字符串逆序一下创造出一个新的字符串
再找出这两个字符串的最长公共子序列 我们找出来的最长公共子序列就是回文子序列 (其实我们可以想想两个指针从一个字符串的两端开始查找)
方法二
递归版本
我们写的递归函数如下
int process(string& str , int L , int R)
它的含义是 我们给定一个字符串str 返回给这个字符串从L到R位置上的最大回文子串
参数含义如下
- str 我们需要知道回文子串长度的字符串
- L 我们需要知道回文子串长度的起始位置
- R 我们需要知道回文子串长度的终止位置
所有的递归函数都一样 我们首先来想base case
这道题目中变化的参数其实就只有L 和 R 所以说我们只需要考虑L和R的base case
如果L和R相等 如果L和R只相差1
if (L == R) { return 1; } if (L == R - 1) { return str[L] == str[R] ? 2 : 1; }
之后我们来考虑下普遍的可能性
- 如果L 和 R就是回文子序列的一部分
- 如果L可能是回文子序列的一部分 R不是
- 如果L不是回文子序列的一部分 R有可能是
我们按照上面的可能性分析写出下面的代码 之后返回最大值即可
int p1 = process(str , L + 1 , R); int p2 = process(str , L , R - 1);int p3 = str[L] == str[R] ? 2 + process(str , L + 1, R - 1) : 0; return max(max(p1 , p2) , p3);
动态规划
我们注意到原递归函数中 可变参数只有L 和 R 所以说我们只需要围绕着L 和 R建立一张二维表就可以
当然 在一般情况下 L是一定小于等于R的 所以说L大于R的区域我们不考虑
我们首先来看base case
if (L == R) { return 1; } if (L == R - 1) { return str[L] == str[R] ? 2 : 1; }
围绕着这个base case 我们就可以填写两个对角线的内容
for (int L = 0; L < str.size(); L++){for(int R = L; R < str.size(); R++){if (L == R){dp[L][R] = 0;}if (L == R-1){dp[L][R-1] = str[L] == str[R] ? 2 : 1;}} }
接下来我们看一个格子普遍依赖哪些格子
int p1 = process(str , L + 1 , R); int p2 = process(str , L , R - 1);int p3 = str[L] == str[R] ? 2 + process(str , L + 1, R - 1) : 0;
从上面的代码我们可以看到 分别依赖于
L+1 R
L , R-1
L+1 , R-1
从图上来分析 黑色的格子依赖于三个红色格子
于是我们就可以沿着对角线来不断的填写数字
横行一直从0开始 纵列一直在变化 所以我们用列来遍历
最后返回dp[0][str.size()-1]即可
int process1(string& str , vector<vector<int>>& dp){for (int L = 0; L < str.size(); L++){for(int R = 0; R < str.size(); R++){if (L == R){dp[L][R] = 1;}if (L == R-1){dp[L][R] = str[L] == str[R] ? 2 : 1;}}} for (int startR = 2; startR < str.size(); startR++){int L = 0;int R = startR;while (R < str.size()){int p1 = dp[L+1][R];int p2 = dp[L][R-1];int p3 = str[L] == str[R] ? 2 + dp[L+1][R-1] : 0;dp[L][R] = max(p1 , max(p2 , p3));L++;R++;}}return dp[0][str.size()-1];}
象棋问题
递归版本
现在给你一个横长为10 纵长为9的棋盘 给你三个参数 x y z
现在一个马从(0 , 0)位置开始运动
提问 有多少种方法使用K步到指定位置 (指定位置坐标随机给出 且一定在棋盘上)
首先我们可以想出这么一个函数
int process(int x , int y , int rest , int a , int b)
它象棋目前在 x y位置 还剩下 rest步 目的地是到 a b位置
让你返回一个最多的路数
我们首先来想base case
- 首先肯定是剩余步数为0 我们要开始判断是否跳到目的地了
- 其次我们还要判断是否越界 如果越界我们直接返回0即可
代码表示如下
if (x < 0 || x > 9 || y < 0 || y > 8){return 0;}if (rest == 0){return (x == a && y ==b) ? 1 : 0;}
接下来我们开始讨论普遍情况 其实就是把马的各个位置跳一遍
int ways = process(x-2 , y+1 , rest-1 , a , b); ways += process(x-1 , y+2 , rest-1 , a , b); ways += process(x+1 , y+2 , rest-1 , a , b); ways += process(x+2 , y+1 , rest-1 , a , b); ways += process(x-2 , y-1 , rest-1 , a, b); ways += process(x-1 , y-2 , rest-1 , a , b); ways += process(x+1 , y-2 , rest-1 , a, b); ways += process(x+2 , y-1 , rest-1 , a ,b);
其实这样子我们的代码就完成了 总体代码如下
int process(int x , int y , int rest , int a , int b)
{if (x < 0 || x > 9 || y < 0 || y > 8){return 0;}if (rest == 0) { return (x == a && y ==b) ? 1 : 0; } int ways = process(x-2 , y+1 , rest-1 , a , b); ways += process(x-1 , y+2 , rest-1 , a , b); ways += process(x+1 , y+2 , rest-1 , a , b); ways += process(x+2 , y+1 , rest-1 , a , b); ways += process(x-2 , y-1 , rest-1 , a, b); ways += process(x-1 , y-2 , rest-1 , a , b); ways += process(x+1 , y-2 , rest-1 , a, b); ways += process(x+2 , y-1 , rest-1 , a ,b); return ways;
}
动态规划
我们对于原递归函数进行观察 可以得知
int process(int x , int y , int rest , int a , int b)
原函数中 变化的参数只有 x y 和rest 于是乎我们可以建立一个三维的数组
x的范围是0 ~ 9 y的范围是0 ~ 8 而rest的范围则是根据我们步数来决定的 0~K
所以说此时我们以X为横坐标 Y为纵坐标 REST为竖坐标
vector<vector<vector<int>>> dp(10 , vector<vector<int>>(9 , vector<int>(8 , 0)));
我们首先看base case分析下
if (x < 0 || x > 9 || y < 0 || y > 8){return 0;}
如果有越界的地方 我们直接返回0即可
if (rest == 0){return (x == a && y ==b) ? 1 : 0;}
在z轴为0的时候 我们只需要将a b 0坐标标记为1即可
nt process1(int k , int a , int b , vector<vector<vector<int>>>& dp)
{ dp[a][b][0] = 1; for (int z = 1; z <= k; z++) { for (int x = 0; x < 10; x++) { for (int y = 0; y < 9; y++) { int ways = pickdp(x-2 , y+1 , z-1, dp);ways += pickdp(x-1 , y+2 , z-1 , dp);ways += pickdp(x+1 , y+2 , z-1 , dp);ways += pickdp(x+2 , y+1 , z-1 , dp);ways += pickdp(x-2 , y-1 , z-1 , dp);ways += pickdp(x-1 , y-2 , z-1 , dp);ways += pickdp(x+1 , y-2 , z-1 , dp); ways += pickdp(x+2 , y-1 , z-1 , dp);dp[x][y][z] = ways;}} }return dp[0][0][k];
}咖啡机问题
给你一个数组arr arr[i]表示第i号咖啡机泡一杯咖啡德时间
给定一个正数N 表示第N个人等着咖啡机泡咖啡 每台咖啡机只能轮流泡咖啡
只有一台洗咖啡机 一次只能洗一个被子 时间耗费a 洗完才能洗下一杯
当然 每个咖啡杯也能自己挥发干净 挥发干净的时间为b 咖啡机可以并行的挥发
假设所有人拿到咖啡之后立刻喝干净
返回从开始等待到所有咖啡机变干净的最短时间
我们首先来分析下题目
这里其实是两个问题
- 问题一 每个人喝咖啡喝完的时间是多少
- 问题二 每个人洗完的时间是多少
对于问题一 我们可以使用一个小根堆来做
我们定义一个机器类 里面有两个成员函数
机器的开始时间和机器的使用时间 我们使用它们相加之和来作为小根堆排序的依据
之后我们就能得到每个人喝完咖啡的最优解了
class Machine
{ public: int _starttime; int _worktime; public: int getsum() const { return _starttime + _worktime; } public: Machine() = default; Machine(int st , int wt) :_starttime(st) ,_worktime(wt) {} bool operator()(const Machine& obj1 , const Machine& obj2) { return obj1.getsum() > obj2.getsum(); }
};
vector<int> process(vector<int>& arr , int num)
{vector<int> ans;priority_queue<Machine , vector<Machine> , Machine> heap;for (auto x : arr) {heap.push(Machine(0 , x));}for (int i = 0; i < num; i++){Machine cur = heap.top();heap.pop();ans.push_back(cur.getsum());cur._starttime += cur._worktime;heap.push(Machine(cur._starttime , cur._worktime));}return ans;
}
递归版本
我们在写递归版本的时候首先要想到递归函数的含义
它的含义是返回一个所有咖啡杯都被洗完的最小值
之后我们可以想base case 当什么样的时候 该函数无法递归了
最后列出所有可能性即可
int process(vector<int>& end , int index , int a , int b , int avltime)
{if (index == static_cast<int>(end.size())){return 0;} // possible 1 int p1 = max(a + end[index] , process(end , index+1 , a , b , avltime)); // possible 2 int p2 = max(b + end[index], process(end , index+1 , a , b , avltime + b)); return min(p1 , p2);
}动态规划
这个问题的动态规划涉及到一个大小问题
因为我们无法确定avltime使用到的时间 所以这里有两种解决方案
- 将它开辟的足够大
- 根据最大值计算 (假设所有人都用咖啡机洗)
int dpprocess(vector<int>& end , int a , int b , vector<vector<int>> dp)
{// dp[N][...] = 0;for (int indexdp = static_cast<int>(end.size()) - 1; indexdp >= 0 ; indexdp--){for (int freetime = 0; freetime <= 10000 ; freetime++){int p1 = max(a + end[indexdp] , dp[indexdp+1][freetime]);int p2 = max(b + end[indexdp] , dp[indexdp+1][freetime+b]);dp[indexdp][freetime] = min(p1 , p2);}}return dp[0][0];
}相关文章:

【Hello Algorithm】暴力递归到动态规划(三)
暴力递归到动态规划(三) 最长公共子序列递归版本动态规划 最长回文串子序列方法一方法二递归版本动态规划 象棋问题递归版本动态规划 咖啡机问题递归版本动态规划 最长公共子序列 这是leetcode上的一道原题 题目连接如下 最长公共子序列 题目描述如下…...

gitLab更新11.11.3->16.1.5
gitlab当前版本11.11.3 postgreSQL当前版本 9.6.11 gitlab升级顺序 11.11.3 -》 12.0.12 -》 12.10.14 -》13.0.14 -》 13.1.11 -》13.8.8 -》13.12.15 -》14.0.12 —》 14.3.6 -》 14.9.5 -》 14.10.5 -》 15.0.5 -》 15.1.6 -》 15.4.6 -》 15.11.13 -》 16.0.X —》 16.…...

12-k8s-HPA自动扩缩容
文章目录 一、k8s弹性伸缩类型二、HPA原理三、metrics-server插件四、创建nginx提供负载测试五、部署HPA master操作即可 一、k8s弹性伸缩类型 Cluster-Autoscale: 集群容量(node数量)自动伸缩,跟自动化部署相关的,依赖iaas的弹性伸缩,主要用…...

从十月稻田,看大米为何能卖出200亿市值?
国无农不稳,民无粮不安。新时代的农村农民,需要现代化的农业作依托,而在农业现代化的过程中,品牌化、数字化成为至关重要的一环。 金秋十月,从南到北,从东到西,中国农村的每一块土地都洋溢着丰…...

功能集成,不占空间,同为科技TOWE嵌入式桌面PDU超级插座
随着现代社会人们生活水平的不断提高,消费者对生活质量有着越来越高的期望。生活中,各式各样的电气设备为我们的生活带来了便利,在安装使用这些用电器时,需要考虑电源插排插座的选择。传统的插排插座设计多暴露于空间之中…...

使用pdf.js预览pdf文件时如何兼容chrome66版本
最近在做一个需求,在PC端实现预览pdf文件的功能,但是要最低兼容chrome的66版本,因为公司用的chrome浏览器最低版本就是66版本。 现在下载PDF.js(链接:https://mozilla.github.io/pdf.js/) 下载下来的版本是…...
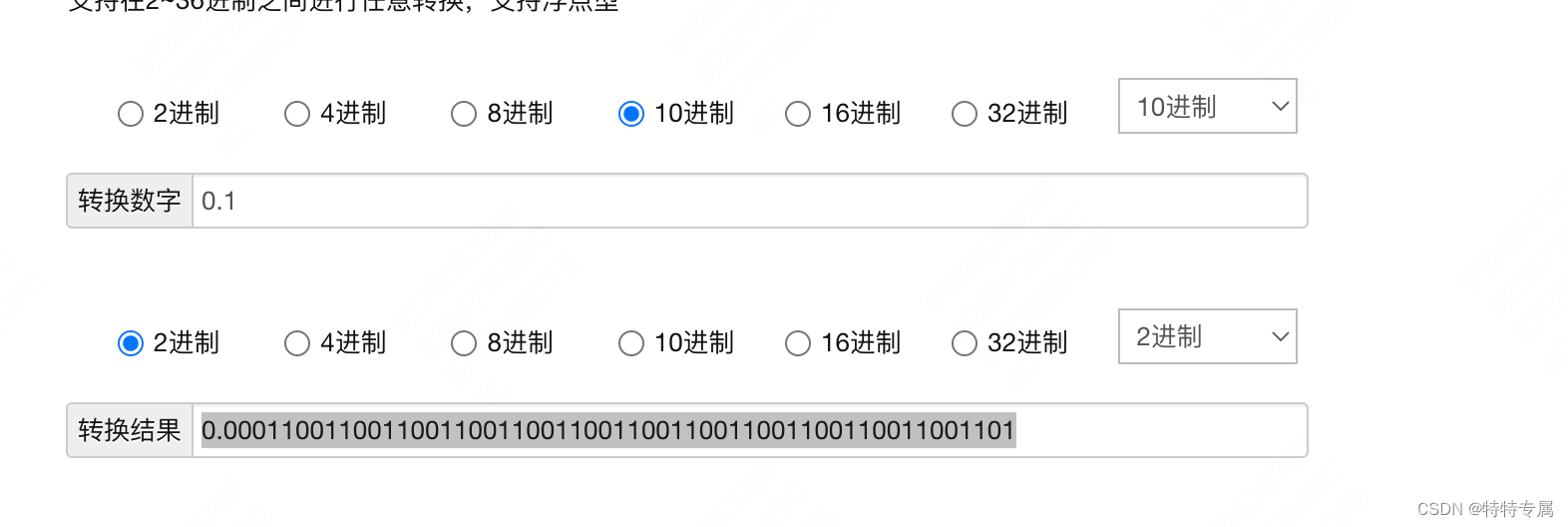
一篇文章讲明白double、float丢失精度的问题
1.背景 1.10.1 1.2000000000000002 发现上面计算的值竟然和数学计算不一致 2. 问题 计算机是通过二进制计算的,如果我们在二进制的视角来看待上面问题,就很容易发现问题了。 例如:把「0.1」转成二进制的表示,然后还原成十进制&…...

Day 2 Qt
#include "my_widget.h" #include "ui_my_widget.h"My_Widget::My_Widget(QWidget *parent): QWidget(parent), ui(new Ui::My_Widget) {ui->setupUi(this);//窗口的相关设置 // this -> resize(800,500);this -> setWindowTitle("QQ聊天…...
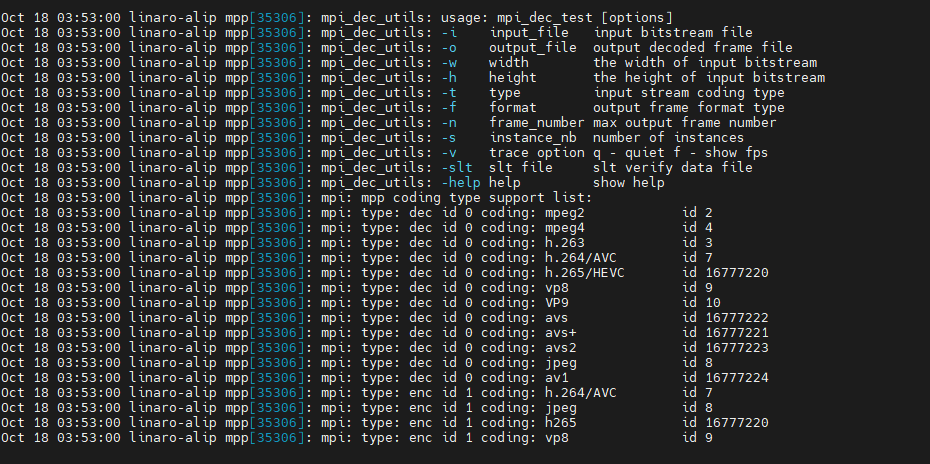
ArmSoM-W3之RK3588 MPP环境配置
1. 简介 瑞芯微提供的媒体处理软件平台(Media Process Platform,简称 MPP)是适用于瑞芯微芯片系列的 通用媒体处理软件平台。该平台对应用软件屏蔽了芯片相关的复杂底层处理,其目的是为了屏蔽不 同芯片的差异,为使用者…...

【C++ 拷贝构造函数详解】
在 C 编程中,拷贝构造函数是一个重要的概念,用于创建一个对象的副本。拷贝构造函数允许你在不改变原始对象的情况下创建一个新的对象,这在很多情况下非常有用。在本篇博客中,我们将详细讨论 C 拷贝构造函数的用法和实现。 什么是…...
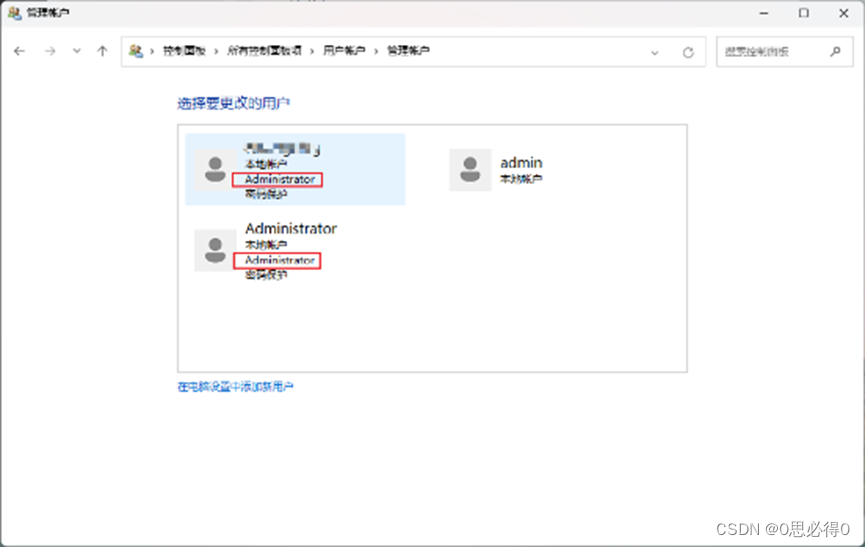
[计算机提升] 用户和用户组
1.1 用户和用户组 1.1.1 用户 用户账户是计算机操作系统中用于标识和管理用户身份的概念。 每个用户都拥有一个唯一的用户账户,该账户包含用户的登录名、密码和其他与用户身份相关的信息。 用户账户通常用于验证用户身份,并授权对系统资源的访问权限。…...
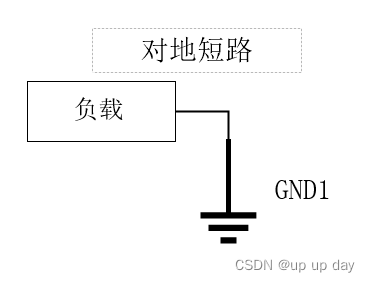
开路、断路和短路区别
文章目录 开路和断路击穿电源短路、用电器短路、对地短路和对电源短路 开路和断路 开路和断路是电路中两种用于描述电流流动情况的状态。 两者易混淆,常被混淆使用,但是它们还是有所不同。 开路表示电路中存在一个断链,电流无法从一个点流到…...

springBoot web开发自动配置和默认效果
web开发自动配置和默认效果 自动配置默认配置 自动配置 绑定了配置文件的一堆配置项 1、springMVC的所有配置 spring.mvc 2、Web场景通用配置 spring.web 3、文件上传配置 spring.servlet.multipart 4、服务器的配置serve: 比如:编码方式等 默认配置 重要…...
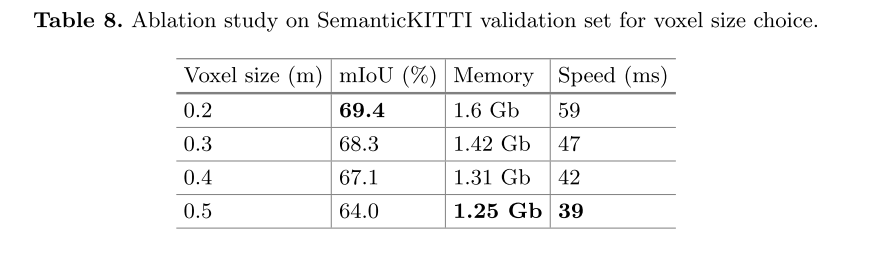
论文阅读:Efficient Point Cloud Segmentation with Geometry-Aware Sparse Networks
来源:ECCV2022 链接:Efficient Point Cloud Segmentation with Geometry-Aware Sparse Networks | SpringerLink 0、Abstract 在点云学习中,稀疏性和几何性是两个核心特性。近年来,为了提高点云语义分割的性能,人们提…...
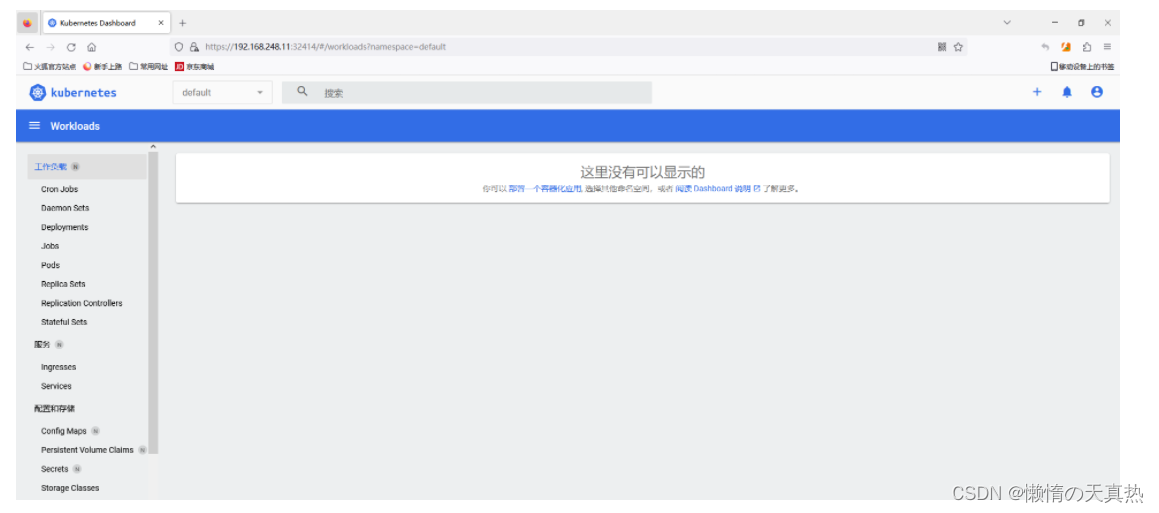
1-k8s1.24-底座搭建-基于containerd
文章目录 一、服务器准备二、安装Containerd三、安装k8s四、安装部署dashboard ps:第一遍搭建ks8的时候,由于k8s在1.24版本之后就放弃了对docker的支持,如果要继续使用docker需要自己加载插件。所以一开始就是直接使用 k8s1.24containerd进行…...

Java文件前后端上传下载工具类
任何非压缩格式下载 package com.pisx.pd.eco.util;import java.io.*; import java.util.Collections; import java.util.HashMap; import java.util.Map;import javax.servlet.ServletOutputStream; import javax.servlet.http.HttpServletResponse;import org.springframewo…...

内燃机可变气门驱动研究进展
Review of Advancement in Variable Valve Actuation of Internal Combustion Engines AbstractIntroduction燃烧和气体交换需要电子控制 paper Abstract 近年来,人们对空气污染和能源使用的日益关注导致了车辆动力总成系统的电气化。 另一方面,一个多世…...

NEFU离散数学实验2-容斥原理
相关概念 离散数学中的容斥原理是一种使用集合运算的技巧,通常用于计算两个或更多集合的并集或交集的大小。以下是一些与容斥原理相关的常见概念和公式。 概念: 1. 集合:由元素组成的对象,通常用大写字母表示,如A、B、…...
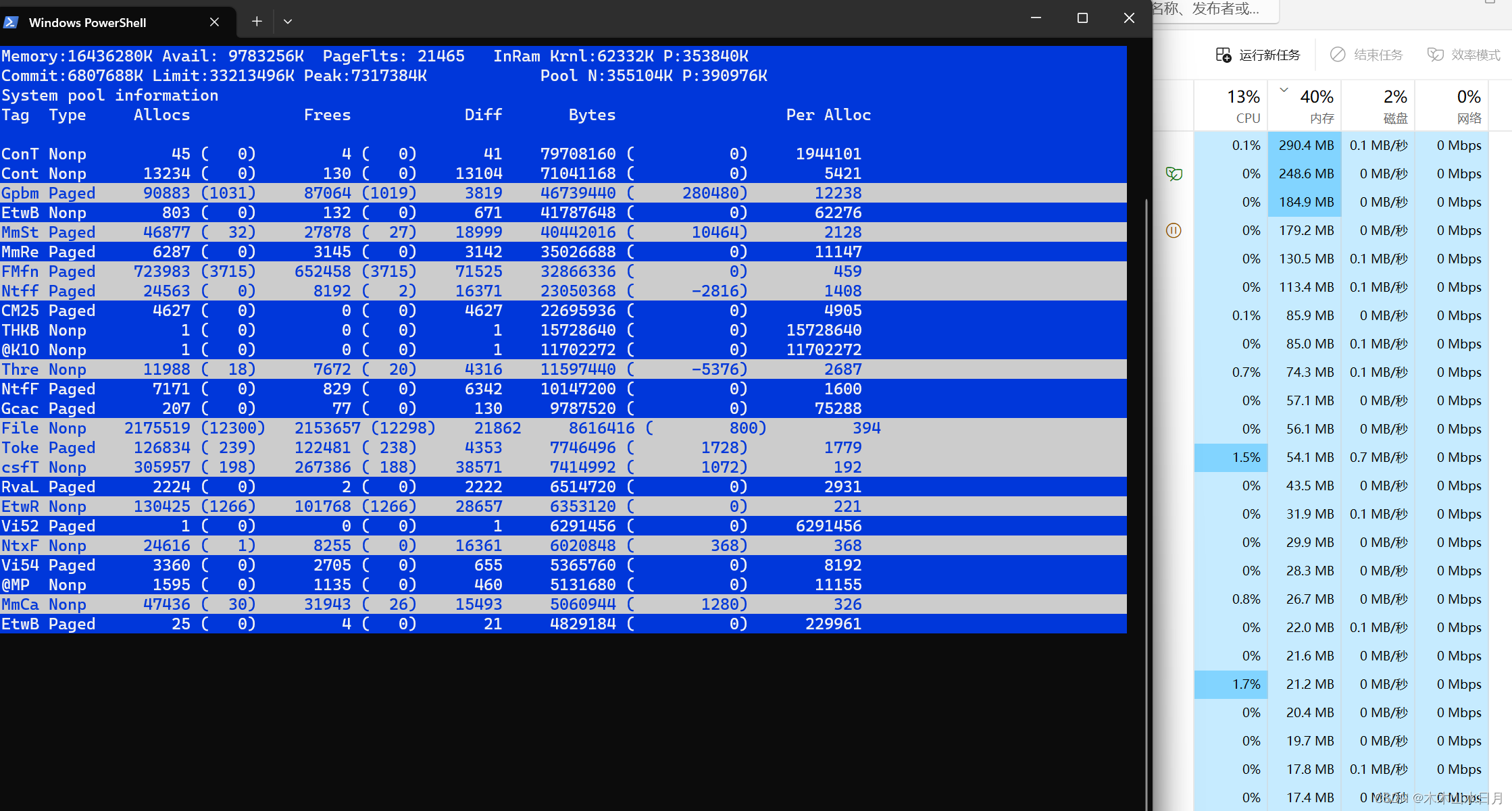
解决Windows内存溢出/占满死机问题-PoolMon工具
某一天, 工作所用笔记本突然越来越卡直至死机 以为只是windows11的抽风行为,之前就因为windows11资源管理器经常卡死(后升级小版本好多了)。 遂长按电源键强制关机重启。 然慢慢又越来越卡,直至卡死,无…...
【ROS】ros-noetic和anaconda联合使用【教程】
【ROS】ros-noetic和anaconda联合使用【教程】 文章目录 【ROS】ros-noetic和anaconda联合使用【教程】1. 安装anaconda2. 创建虚拟环境3. 查看python解释器路径4. 在虚拟环境中使用任意的包5. 创建工作空间和ros功能包进行测试Reference 1. 安装anaconda 在Ubuntu20.04中安装…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Neko虚拟浏览器远程协作方案:Docker+内网穿透技术部署实践
前言:本文将向开发者介绍一款创新性协作工具——Neko虚拟浏览器。在数字化协作场景中,跨地域的团队常需面对实时共享屏幕、协同编辑文档等需求。通过本指南,你将掌握在Ubuntu系统中使用容器化技术部署该工具的具体方案,并结合内网…...
