第 367 场 LeetCode 周赛题解
A 找出满足差值条件的下标 I

模拟
class Solution {
public:vector<int> findIndices(vector<int> &nums, int indexDifference, int valueDifference) {int n = nums.size();for (int i = 0; i < n; i++)for (int j = 0; j <= i; j++)if (i - j >= indexDifference && abs(nums[i] - nums[j]) >= valueDifference)return {i, j};return {-1, -1};}
};
B 最短且字典序最小的美丽子字符串

枚举:先枚举美丽子字符串的长度以求其最短长度 l e n len len ,然后遍历求长为 l e n len len 的字典序最小的美丽子字符串。
class Solution {
public:string shortestBeautifulSubstring(string s, int k) {int n = s.size();vector<int> ps(n + 1);//前缀和for (int i = 0; i < n; i++)ps[i + 1] = ps[i] + (s[i] == '1' ? 1 : 0);for (int len = k; len <= n; len++) {int find = 0;for (int i = 0, j = i + len - 1; j < n; i++, j++) {if (ps[j + 1] - ps[i] == k)//子字符串s[i,j]中1的个数恰好等于 kfind = 1;}string res = "";if (find) {for (int i = 0, j = i + len - 1; j < n; i++, j++) {if (ps[j + 1] - ps[i] == k) {if (res.empty() || s.substr(i, len) < res)res = s.substr(i, len);}}return res;}}return "";}
};
C 找出满足差值条件的下标 II

前缀极值:设 j ≤ i j\le i j≤i ,且 i − j ≥ i n d e x D i f f e r e n c e i-j\ge indexDifference i−j≥indexDifference,为了使 a b s ( n u m s [ i ] − n u m s [ j ] ) abs(nums[i]-nums[j]) abs(nums[i]−nums[j]) 尽量大, n u m s [ i ] nums[i] nums[i] 应该尽量小或尽量大,所以预处理求出前缀极小值数组 m n mn mn ( m n [ i ] = a r g m i n 0 ≤ k ≤ i { n u m s [ k ] } mn[i]=argmin_{0\le k\le i} \{nums[k]\} mn[i]=argmin0≤k≤i{nums[k]} )和前缀极大值数组 m x mx mx( m x [ i ] = a r g m a x 0 ≤ k ≤ i { n u m s [ k ] } mx[i]=argmax_{0\le k\le i} \{nums[k]\} mx[i]=argmax0≤k≤i{nums[k]} ),然后枚举 i i i 。
class Solution {
public:vector<int> findIndices(vector<int> &nums, int indexDifference, int valueDifference) {int n = nums.size();int mx[n], mn[n];mx[0] = 0;mn[0] = 0;for (int i = 1; i < n; i++) {mx[i] = nums[mx[i - 1]] > nums[i] ? mx[i - 1] : i;mn[i] = nums[mn[i - 1]] < nums[i] ? mn[i - 1] : i;}for (int i = 0; i < n; i++) {if (i - indexDifference >= 0) {if (abs(nums[i] - nums[mx[i - indexDifference]]) >= valueDifference)return {i, mx[i - indexDifference]};if (abs(nums[i] - nums[mn[i - indexDifference]]) >= valueDifference)return {i, mn[i - indexDifference]};}}return {-1, -1};}
};
D 构造乘积矩阵

前后缀处理:设 p r e [ i ] pre[i] pre[i] 为前 i + 1 i+1 i+1 行元素之积,设 s u f [ i ] suf[i] suf[i] 为后 g r i d . s i z e ( ) − i grid.size()-i grid.size()−i 行元素之积,设 l e f t [ i ] [ j ] left[i][j] left[i][j] 为第 i i i 行前 j + 1 j+1 j+1 个
元素之积,设 r i g h t [ i ] [ j ] right[i][j] right[i][j] 为第 i i i 行后 g r i d [ 0 ] . s i z e ( ) − j grid[0].size()-j grid[0].size()−j 个元素之积,则 p [ i ] [ j ] = p r e [ i − 1 ] × s u f [ i + 1 ] × l e f t [ i ] [ j − 1 ] × r i g h t [ i ] [ j + 1 ] p[i][j]=pre[i-1]\times suf[i+1] \times left[i][j-1]\times right[i][j+1] p[i][j]=pre[i−1]×suf[i+1]×left[i][j−1]×right[i][j+1]
class Solution {
public:using ll = long long;vector<vector<int>> constructProductMatrix(vector<vector<int>> &grid) {int m = grid.size(), n = grid[0].size();int mod = 12345;vector<vector<int>> res(m, vector<int>(n));vector<ll> row(m, 1), pre(m, 1), suf(m, 1);for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++)row[i] = row[i] * grid[i][j] % mod;pre[i] = i != 0 ? pre[i - 1] * row[i] % mod : row[i];}for (int i = m - 1; i >= 0; i--)suf[i] = i != m - 1 ? suf[i + 1] * row[i] % mod : row[i];vector<ll> left(n), right(n);for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++)left[j] = j != 0 ? left[j - 1] * grid[i][j] % mod : grid[i][j];for (int j = n - 1; j >= 0; j--)right[j] = j != n - 1 ? right[j + 1] * grid[i][j] % mod : grid[i][j];int other = (i != 0 ? pre[i - 1] : 1) * (i != m - 1 ? suf[i + 1] : 1) % mod;for (int j = 0; j < n; j++)res[i][j] = other * (j != 0 ? left[j - 1] : 1) % mod * (j != n - 1 ? right[j + 1] : 1) % mod;}return res;}
};
相关文章:

第 367 场 LeetCode 周赛题解
A 找出满足差值条件的下标 I 模拟 class Solution { public:vector<int> findIndices(vector<int> &nums, int indexDifference, int valueDifference) {int n nums.size();for (int i 0; i < n; i)for (int j 0; j < i; j)if (i - j > indexDiffe…...
最新百度统计配置图文教程,获取siteId、百度统计AccessToken、百度统计代码教程
一、前言 很多网友开发者都不知道百度统计siteId、百度统计token怎么获取,在网上找的教程都是几年前老的教程,因此给大家出一期详细百度统计siteId、百度统计token、百度统计代码获取详细步骤教程。 二、登录到百度统计 1.1 登录到百度统计官网 使用…...

【C++ 学习 ㉘】- 详解 C++11 的列表初始化
目录 一、C11 简介 二、列表初始化 2.1 - 统一初始化 2.2 - 列表初始化的使用细节 2.2.1 - 聚合类型的定义 2.2.2 - 注意事项 2.3 - initializer_list 2.3.1 - 基本使用 2.3.2 - 源码剖析 一、C11 简介 1998 年,C 标准委员会发布了第一版 C 标准࿰…...

OpenCV12-图像卷积
OpenCV12-图像卷积 图像卷积 图像卷积 OpenCV中提供了filt2D()函数用于实现图像和卷积模板之间的卷积运算: void filter2D(InputArray src, // 输入图像OutputArray dst, // 输出图像int ddepth, // 输出图像数据类型(深度)ÿ…...
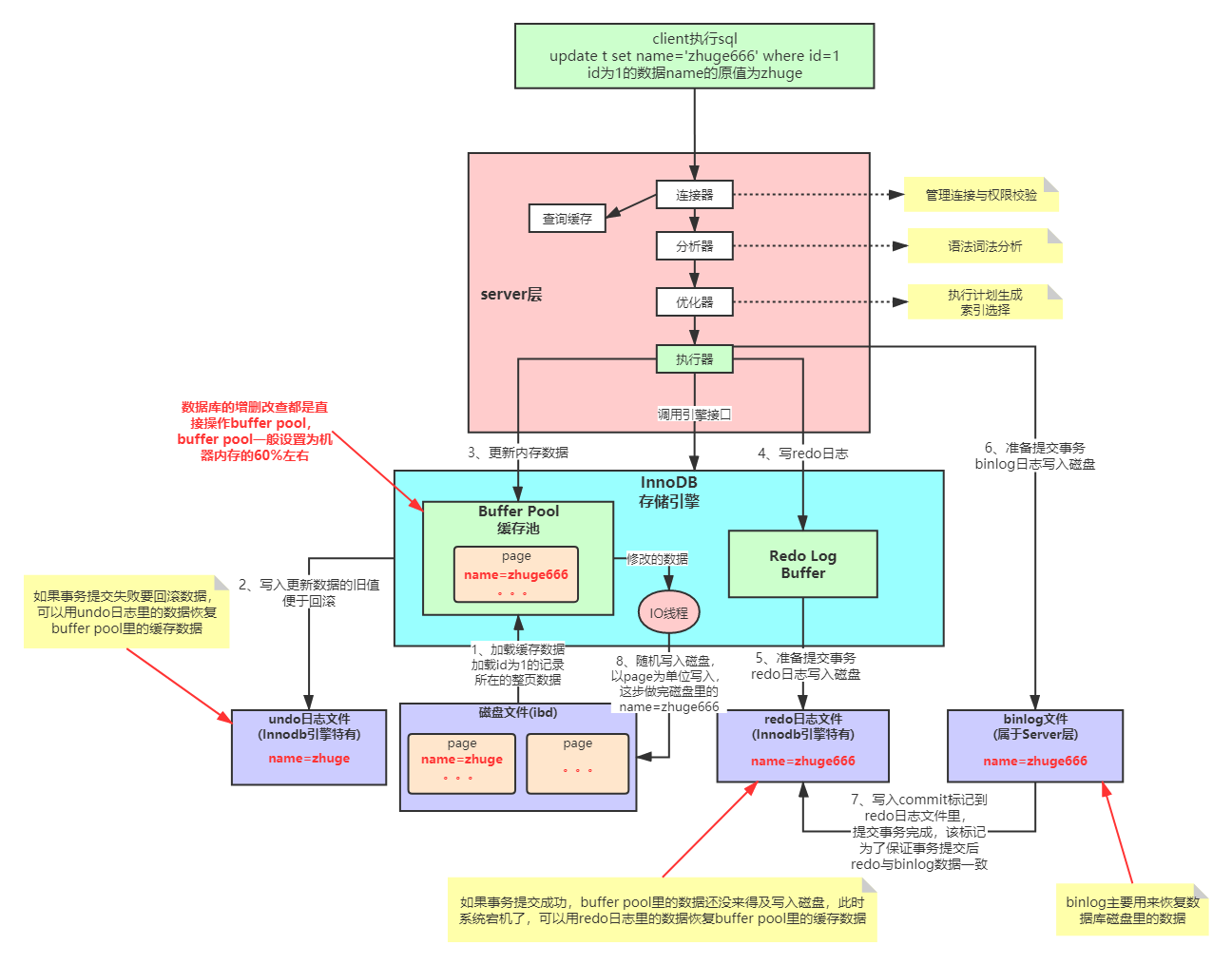
MVCC与BufferPool缓存机制
MVCC多版本并发控制机制 Mysql在可重复读隔离级别下如何保证事务较高的隔离性,我们上节课给大家演示过,同样的sql查询语句在一个事务里多次执行查询结果相同,就算其它事务对数据有修改也不会影响当前事务sql语句的查询结果。 这个隔离性就是…...
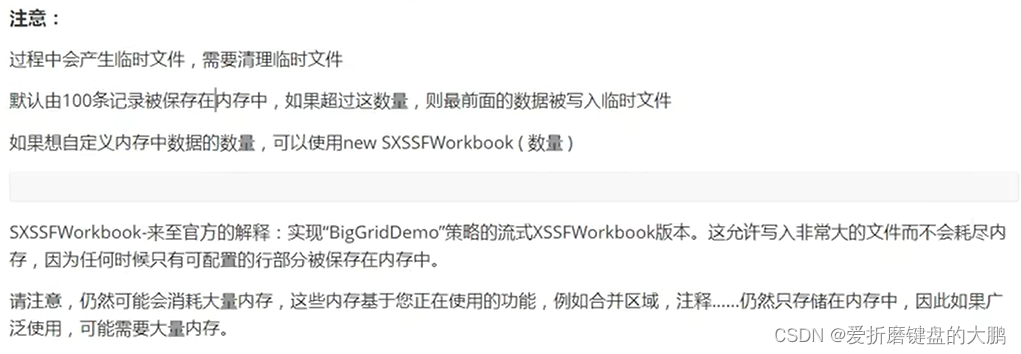
POI、Easy Excel操作Excel
文章目录 1.常用的场景2.基本功能3.Excel在Java中是一个对象4. 简单的写(07版本(.xlsx)Excel)大文件写HSSF大文件写XSSF大文件写SXSSF 5. Excel读5.1 读取遇到类型转化问题该怎么解决5.2 遇到Excel公式怎么办 6. Easy Excel6.1简单…...

网络安全(黑客)自学方向
每年报考网络安全专业的人数很多,但不少同学听说千万别学网络安全,害怕网络安全专业很难就业。下面就带大家深入了解一下网络安全专业毕业后可以干什么,包括网络安全专业的就业前景和方向等。 随着信息化时代的到来,网络安全行业…...

react写一个简单的3d滚轮picker组件
1. TreeDPicker.tsx文件 原理就不想赘述了, 想了解的话, 网址在: 使用vue写一个picker插件,使用3d滚轮的原理_vue3中支持3d picker选择器插件-CSDN博客 import React, { useEffect, useRef, Ref, useState } from "react"; import Animate from "../utils/an…...

Compose竖向列表LazyColumn
基础列表一 LazyColumn组件中用items加载数据,rememberLazyListState()结合rememberCoroutineScope()实现返回顶部。 /*** 基础列表一*/ Composable fun Items() {Box(modifier Modifier.fillMaxSize()) {val context LocalContext.currentval dataList arrayLi…...

6.自定义相机控制器
愿你出走半生,归来仍是少年! Cesium For Unity自带的Dynamic Camera,拥有优秀的动态展示效果,但是其对于场景的交互方式用起来不是很舒服。 通过模仿Cesium JS 的交互方式,实现在Unity中的交互: 通过鼠标左键拖拽实现场景平移通过…...
一文带你GO语言入门
什么是go语言? Go语言(又称Golang)是Google开发的一种静态强类型、编译型、并发型,并具有垃圾回收功能的编程语言。Go语言的主要特点包括:- 简洁和简单 - 语法简单明快,易于学习和使用 特点 高效 编译速度快,执行效率高 并发支持 原生支持并发,利用goroutine实现高效的并发…...

前后端小项目链接
1.vue的创建 vue的项目创建 1.1 vue create vue_name 1.2 Babel Router(路由) CSS Pre-processors 路由可通过:npm i vue-router3.5.2 -S 下载 1.3less 1.4 In dedicated config files 1.5 启动命令:npm run serve 端口号在vue.config。js中配置 devS…...
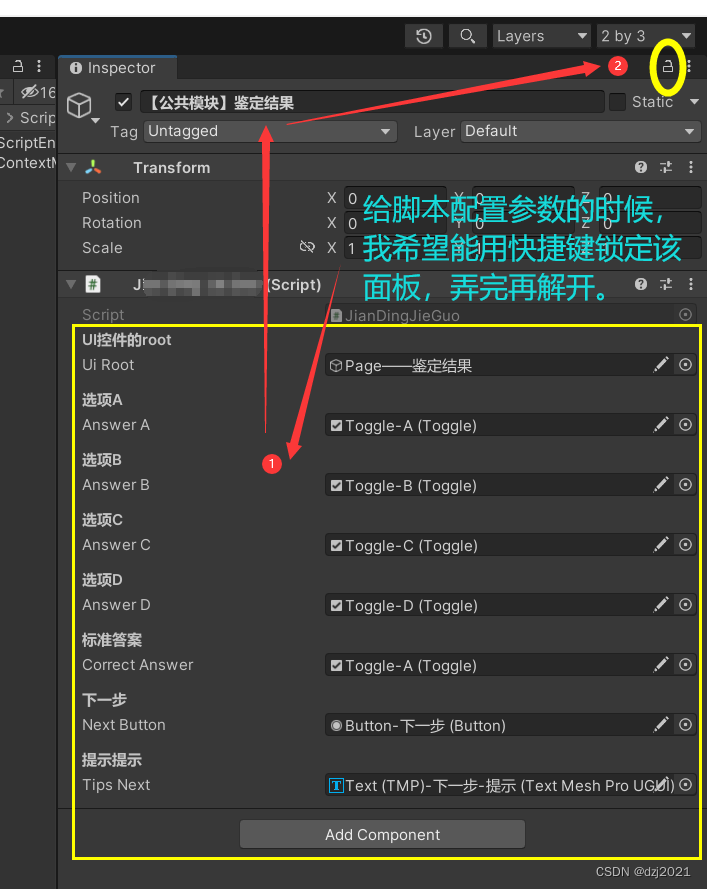
编辑器功能:用一个快捷键来【锁定】或【解开】Inspector面板
一、需求 我有一个脚本,上面暴露了许多参数,我要在场景中拖物体给它进行配置。 如果不锁定Inspector面板的话,每次点击物体后,Inspector的内容就是刚点击的物体的内容,而不是挂载脚本的参数面板。 二、 解决 &…...

Vue 网络处理 - axios 异步请求的使用,请求响应拦截器(最佳实践)
目录 一、axiox 1.1、axios 简介 1.2、axios 基本使用 1.2.1、下载核心 js 文件. 1.2.2、发送 GET 异步请求 1.2.3、发送 POST 异步请求 1.2.4、发送 GET、POST 请求最佳实践 1.3、请求响应拦截器 1.3.1、拦截器解释 1.3.2、请求拦截器的使用 1.3.3、响应拦截器的使…...
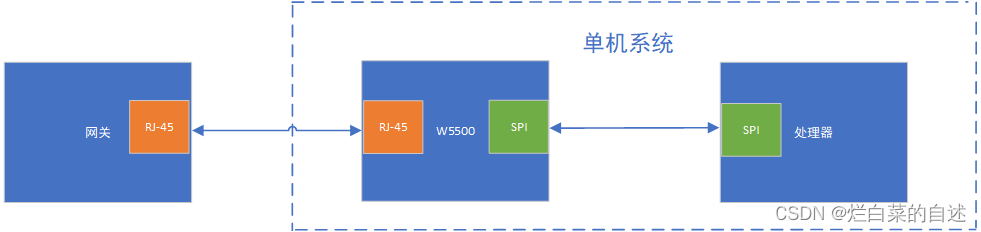
关于W5500网卡使用过程的部分问题记录
某个项目中用到了W5500这种自带网络协议栈的网卡芯片,由于该项目开发时间很紧,就临时网上买了一些模块拼凑到了一套系统,经过验证果真这种拼积木的方法只能用在学生实验开发中,真不能拿来做工程应用,硬件太不稳定很容易…...

Unity DOTS World Entity ArchType Component EntityManager System概述
最近DOTS终于发布了正式的版本, 我们来分享以下DOTS里面地几个关键概念,方便大家上手学习掌握Unity DOTS开发。 Unity DOTS 中所有的Entities 都是被放到World世界中。每个Entity在它所在的World里面有唯一不同的ID号来区分。DOTS项目中可以同时有多个World。每个W…...
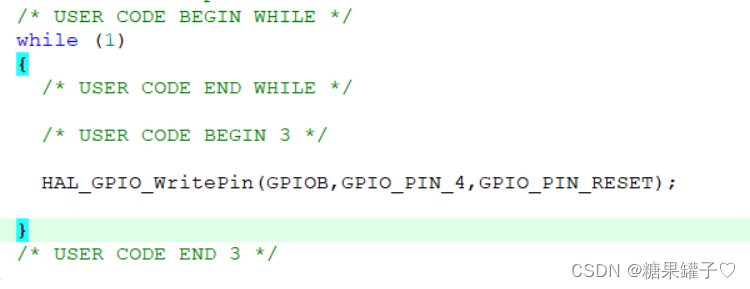
最详细STM32,cubeMX 点亮 led
这篇文章将详细介绍 如何在 stm32103 板子上点亮一个LED. 文章目录 前言一、开发环境搭建。二、LED 原理图解读三、什么是 GPIO四、cubeMX 配置工程五、解读 cubeMX 生成的代码六、延时函数七、控制引脚状态函数点亮 LED 八、GPIO 的工作模式九、为什么使用推挽输出驱动 LED总结…...
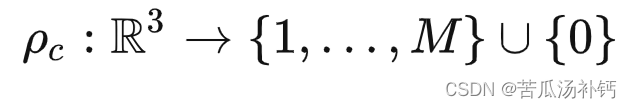
论文阅读:Image-to-Lidar Self-Supervised Distillation for Autonomous Driving Data
目录 摘要 Motivation 整体架构流程 技术细节 雷达和图像数据的同步 小结 论文地址: [2203.16258] Image-to-Lidar Self-Supervised Distillation for Autonomous Driving Data (arxiv.org) 论文代码:GitHub - valeoai/SLidR: Official PyTorch implementati…...

前端版本控制工具,常见的Git 和SVN
目录 前言GitGit简介Git的优势Git常用指令常见的Git服务 SVN (Subversion)SVN简介SVN的优势SVN常用指令SVN与Git的区别 👍 点赞,你的认可是我创作的动力! ⭐️ 收藏,你的青睐是我努力的方向! ✏️ 评论,你…...
C++ —— Tinyxml2在Vs2017下相关使用2(较文1更复杂,附源码)
相关链接 C —— Tinyxml2在Vs2017下相关使用1(附源码) tinyxml2简介 TinyXML2是一个简单,小巧,高效,CXML解析器,可以很容易地集成到其他程序中。TinyXML-2解析一个XML文档,并从中构建一个 可以…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

Python爬虫实战:研究Restkit库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的有价值数据。如何高效地采集这些数据并将其应用于实际业务中,成为了许多企业和开发者关注的焦点。网络爬虫技术作为一种自动化的数据采集工具,可以帮助我们从网页中提取所需的信息。而 RESTful API …...
)
2025.6.9总结(利与弊)
凡事都有两面性。在大厂上班也不例外。今天找开发定位问题,从一个接口人不断溯源到另一个 接口人。有时候,不知道是谁的责任填。将工作内容分的很细,每个人负责其中的一小块。我清楚的意识到,自己就是个可以随时替换的螺丝钉&…...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...
