数据结构详细笔记——栈与队列
文章目录
- 栈的三要素
- 逻辑结构(定义)
- 数据的运算(基本操作)
- 存储结构(物理结构)
- 顺序栈(顺序存储)
- 链栈(链式存储)
- 队列的三要素
- 逻辑结构(定义)
- 数据的运算(基本操作)
- 存储结构(物理结构)
- 顺序队列(顺序存储)
- 链式队列(链式存储)
- 队列的变种
- 栈在括号匹配中的应用
- 栈在表达式求值中的应用
- 中缀表达式 ------>后缀表达式
- 后缀表达式的计算
- 中缀表达式 ------>前缀表达式
- 前缀表达式的计算
- 用栈实现中缀表达式的计算
栈的三要素
逻辑结构(定义)
栈是只允许在一端进行插入或删除操作的线性表
特点:后进先出(LIFO)
数据的运算(基本操作)
InitStack(&S)
初始化栈:构造一个空栈S,分配内存空间DestroyStack(&S)
销毁栈:销毁并释放栈S所占用的内存空间Push(&S,x)
进栈:若栈S未满,则将x加入使之成为新栈顶Pop(&S,&x)
出栈:若栈非空,则弹出栈顶元素,并用x返回GetTop(S,&x)
读栈顶元素:若栈S非空,则用x返回栈顶元素StackEmpty(S)
判断一个栈S是否为空,若S为空,则返回true,否则返回false
栈的常考题型
已知进栈顺序,问有哪些合法的出栈顺序?
出栈元素不同排列的个数为
存储结构(物理结构)
顺序栈(顺序存储)
顺序栈的定义
#define MaxSize 10
typedef struct{ELemType data[MaxSize]; // 静态数组存放栈中元素int top; // 栈顶指针
}SqStack;
初始化栈
void InitStack(SqStack &S){S.top = 0;
}
判空
bool StackEmpty(SqStack S){if(S.top == -1)return true;elsereturn false;
]
进栈操作
bool Push(SqStack &S,ElemType x){if(S.top == MaxSize - 1)renturn false;S.top = S.top + 1; // 指针先加1S.data[S.top] = x; // 新元素入栈return true;
}
出栈操作
bool Pop(SqStack &S, ElemType &x){if(S.top == -1)return false;x = S.data[S.top];S.top = S.top - 1;return true;
}
读栈顶元素
bool GetTop(SqStack S, ElemType &x){if(S.top == -1)return false;x = S.data[S.top];return true;
|
共享栈
#define MaxSize 10
typedef struct{ElemType data[MaxSize];int top0; // 0号栈栈顶指针int top1; // 1号栈栈顶指针
} ShStack;// 初始化栈
void InitStack(ShStack &S){S.top0 = -1;S.top1 = MaxSize;
}
栈满的条件: top0 + 1 = top1
链栈(链式存储)
链栈的定义
其操作相当于头插法建立单链表(只从表头进行增加删除操作)
typedef struct LinkNode{ELemType data; // 数据域struct LinkNode *next; // 指针域
}*LinkStack;
队列的三要素
逻辑结构(定义)
队列是只允许在一端进行插入,在另一端删除的线性表
特点:先进先出(FIFO)
数据的运算(基本操作)
InitQueue(&Q)
初始化队列:构造一个空队列QDestroyQueue(&Q)
销毁队列:销毁并释队列Q所占用的内存空间EnQueue(&Q,x)
入队:若队列Q未满,则将x加入使之成为新的队尾DeQueue(&Q,&x)
出队:若队列非空,删除队头元素,并用x返回GetHead(Q,&x)
读队头元素:若队列Q非空,则用x返回队头元素QueueEmpty(Q)
判断一个队列Q是否为空,若Q为空,则返回true,否则返回false
存储结构(物理结构)
顺序队列(顺序存储)
队列的顺序实现
#define MaxSize 10
typedef struct{ElemType data[MaxSize];int front,rear;
} SqQueue;
初始化队列
void InitQueue(SqQueue &Q){Q.rear = Q.front = 0;
}
判断队列是否为空
bool QueueEmpty(SqQueue Q){if(Q.rear == Qfront)return true;elsereturn false;
}
入队
bool EnQueue(SqQueue &Q,ElemType x){if((Q.rear + 1) % MaxSize == Q.front)return false; //队满则报错Q.data[Q.rear] = x;Q.rear = (Q.rear + 1) % MaxSize; //队尾指针加一取模return true;
}
出队
bool DeQueue(SqQueue &Q,ElemType &x){if(Q.rear == Q.front)return false; // 队空则报错x = Q.data[Q.front];Q.front = (Q.front + 1) % MaxSize;return true;
}
获取队头元素的值,用x返回
bool GetHead(SqQueue Q,ElemType &x){if(Q.rear == Q.front)return false;x = Q.data[Q.front];return true;
}
队列元素的个数:
(rear - front + MaxSzie)% MaxSize
链式队列(链式存储)
队列的链式实现
typedef struct LinkNode{ // 链式队列结点ElemType data; struct LinkNode *next;
}LinkNode;typedef struct{ // 链式队列LinkNode *front,*rear; // 队列的队头和队尾指针
}LinkQueue;
初始化(带头结点)
void InitQueue(LinkQueue &Q){// 初始化 front、rear 都指向头结点Q.front = Q.rear = (LinkNode *) malloc(sizeof(LinkNode));Q.front->next = NULL;
}
队列是否为空
bool IsEmpty(LinkQueue Q){if(Q.rear == Qfront)return true;elsereturn false;
}
新元素入队(带头结点)
void EnQueue(LinkNode &Q,ElemType x){LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));s->data = x;s->next = null;Q.rear->next = s;Q.rear = s;
}
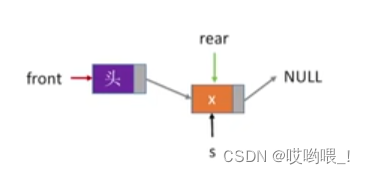
入队(不带头结点)
void EnQueue(LinkQueue &Q,ElemType x){LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));s->data = x;s->next = NULL;if(Q.front == NULL){ // 在空队列中插入第一个元素Q.front = s; // 修改队头队尾的指针Q.rear = s;} else{Q.rear->next = s;Q.rear = s;}
}
出队(带头结点)
bool DeQueue(LinkQueue &Q,ElemType &x){if(Q.front == Q.rear)return false; // 空队LinkNode *p = Q.front->next;x = p.data;Q.front->next = p->next;if(Q.rear == p) // 此次是最后一个结点出队Q.rear = Q.front;free(p); // 释放结点空间return true;
}
出队(不带头结点)
bool DeQueue(LinkQueue &Q,ElemType &x){if(Q.front == NULL)return false;LinkNode *p = Q.front;x = p->data;Q.front = p->next;if(Q.rear = p)[Q.front = NULL;Q.rear = NULL;}free(p);return true;
}
队列的变种
双端队列:允许从两端插入、两端删除的队列
输入受限的双端队列:允许从两端删除、从一端插入的队列
输出受限的双端队列:允许从两端插入、从一端删除的队列
考点:对输出序列的合法性的判断
栈在括号匹配中的应用
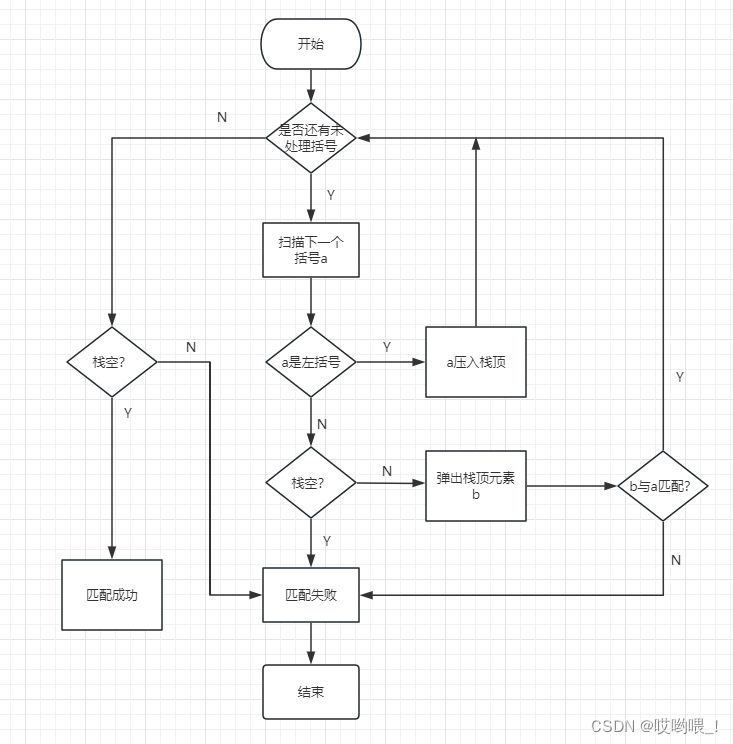
代码实现
#define MaxSize 10
typedef struct{char data[MaxSize];int top;
}SqStack;// 初始化栈
void InitStack(SqStack &S)// 判断栈是否为空
bool StackEmpty(SqStack S)// 新元素入栈
bool Push(SqStack &S,char x)// 栈顶元素出栈,用x返回
bool Pop(SqStack &S,char &x)bool bracketCheck(char str[],int length){SqStack S;InitStack(S); // 初始化for(int i = 0; i < length; i++){if(str[i] == '(' || str[i] == '[' || str[i] == '{'){Push(S, str[i]); // 扫描到左括号,入栈} else {if(StackEmpty(S)) // 扫描到右括号,并且当前栈空return false; // 匹配失败char topElem;Pop(S, topElem); // 栈顶元素出栈if(str[i] == ')' && topElem != '(')return false;if(str[i] == ']' && topElem != '[')return false;if(str[i] == '}' && topElem != '{')return false;}}return StackEmpty(S); // 检索完全部括号后,栈空说明匹配成功
}
栈在表达式求值中的应用
三种算术表达式:
1、中缀表达式:运算符在两个操作数中间 —— a+b
2、后缀表达式(逆波兰表达式):运算符在两个操作数后面 —— ab+
3、前缀表达式(波兰表达式):运算符在两个操作数前面 —— +ab
中缀表达式 ------>后缀表达式
手算
1、确定中缀表达式中各个运算符的运算顺序
2、选择下一个运算符,按照【 左操作符 右操作符 运算符 】的方式组合成一个新的操作数
3、如果还有运算符没被处理,就继续2
注意:为了保证手算和机算结果相同,采用“左优先”原则:只有左边的运算符能先运算,就优先算左边(可保证运算顺序唯一)
机算
初始化一个栈,用于保存暂时还不能确定运算顺序的运算符
从左到右处理各个元素,直到末尾,可能遇到三种情况:
1、遇到操作数:直接加入后缀表达式
2、遇到界限符:遇到 “ ( ” 直接入栈,遇到 “ ) ” 则依次弹出栈内运算符并加入后缀表达式,直到弹出 “ ( ” 为止。注意:“ ( ” 不加入后缀表达式
3、遇到运算符:依次弹出栈中优先级高于或者等于当前运算符的所有运算符,并加入后缀表达式,若碰到 “ ( ” 或栈空则停止。之后再把当前的运算符入栈
4、处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式
后缀表达式的计算
1、从左往右扫描下一个元素,直到处理完所有的元素
2、若扫描到操作数则压入栈,并回到1;否则执行3
3、若扫描到运算符,则弹出两个栈顶元素,执行相应运算(先出栈的是右操作数),运算结果压回栈顶,回到1
4、若表达式合法。则最后栈中只会留下一个元素,就是最终结果
中缀表达式 ------>前缀表达式
1、确定中缀表达式中各个运算符的运算顺序
2、选择下一个运算符,按照【 运算符 左操作符 右操作符 】的方式组合成一个新的操作数
3、如果还有运算符没被处理,就继续2
注意:为了保证手算和机算结果相同,采用“右优先”原则:只有右边的运算符能先运算,就优先算右边(可保证运算顺序唯一)
前缀表达式的计算
1、从右往左扫描下一个元素,直到处理完所有的元素
2、若扫描到操作数则压入栈,并回到1;否则执行3
3、若扫描到运算符,则弹出两个栈顶元素,执行相应运算(先出栈的是左操作数),运算结果压回栈顶,回到1
4、若表达式合法。则最后栈中只会留下一个元素,就是最终结果
用栈实现中缀表达式的计算
中缀表达式 ------>后缀表达式 与 后缀表达式的计算 的结合
*初始化两个栈:操作数栈 和 运算符栈
若扫描到操作数,压入操作数栈
若扫描到运算符或者界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈
每当弹出一个运算符时,就需要在弹出两个操作数栈的栈顶元素并执行相应的运算,运算结果再压回操作数栈中
相关文章:

数据结构详细笔记——栈与队列
文章目录 栈的三要素逻辑结构(定义)数据的运算(基本操作)存储结构(物理结构)顺序栈(顺序存储)链栈(链式存储) 队列的三要素逻辑结构(定义…...

JVM调试命令与调试工具
目录 一、JDK自带命令 1、jps 2、jstat(FullGC频繁解决方案) 3、jmap 4、jhat 5、jstack(cpu占用高解决方案) 6、jinfo 二、JDK的可视化工具JConsole 1、JConsole 2、VisualVM 一、JDK自带命令 Sun JDK监控和故障处理命令如: 1、jps JVM Proc…...
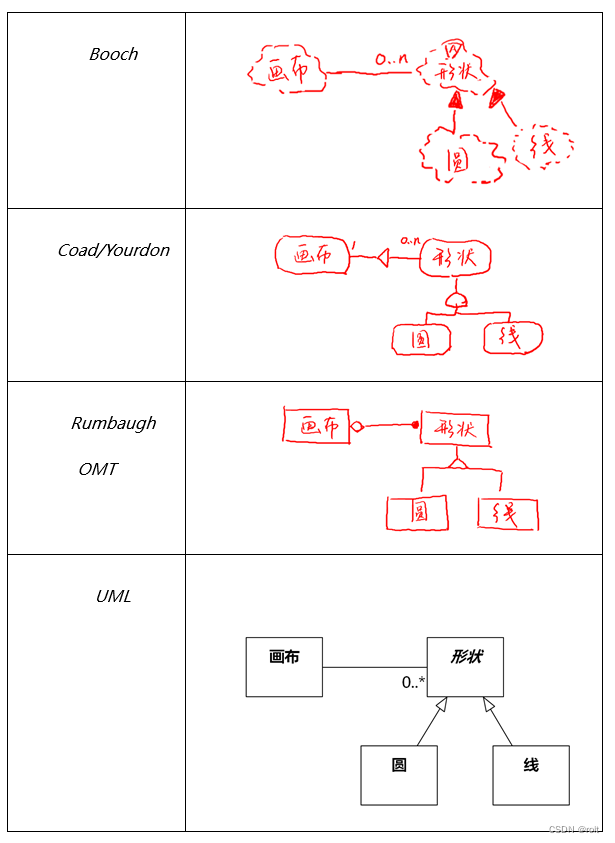
《软件方法》第1章2023版连载(07)UML的历史和现状
DDD领域驱动设计批评文集 做强化自测题获得“软件方法建模师”称号 《软件方法》各章合集 1.3 统一建模语言UML 1.3.1 UML的历史和现状 上一节阐述了A→B→C→D的推导是不可避免的,但具体如何推导,有各种不同的做法,这些做法可以称为“方…...
)
chromium 54 chrome 各个版本发布功能列表(109-119)
chromium Features 109-119 From https://chromestatus.com/features chromium109 Features:12 Auto range support for font descriptors inside font-face rule Auto range support for variable fonts in ‘font-weight’, ‘font-style’ and ‘font-stretch’ descrip…...
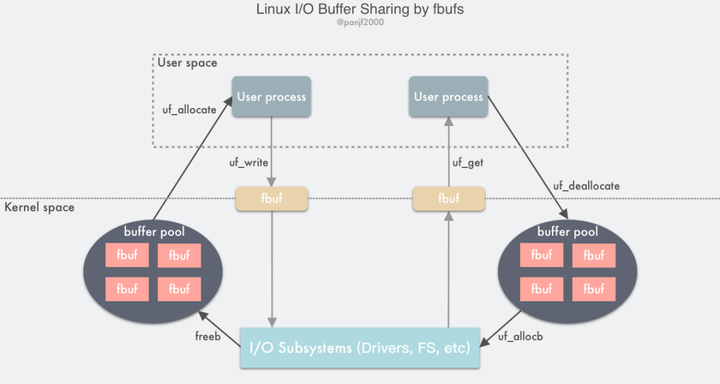
Linux实现原理 — I/O 处理流程与优化手段
Linux I/O 接口 Linux I/O 接口可以分为以下几种类型: 文件 I/O 接口:用于对文件进行读写操作的接口,包括 open()、read()、write()、close()、lseek() 等。 网络 I/O 接口:用于网络通信的接口,包括 socket()、conne…...

第 367 场 LeetCode 周赛题解
A 找出满足差值条件的下标 I 模拟 class Solution { public:vector<int> findIndices(vector<int> &nums, int indexDifference, int valueDifference) {int n nums.size();for (int i 0; i < n; i)for (int j 0; j < i; j)if (i - j > indexDiffe…...
最新百度统计配置图文教程,获取siteId、百度统计AccessToken、百度统计代码教程
一、前言 很多网友开发者都不知道百度统计siteId、百度统计token怎么获取,在网上找的教程都是几年前老的教程,因此给大家出一期详细百度统计siteId、百度统计token、百度统计代码获取详细步骤教程。 二、登录到百度统计 1.1 登录到百度统计官网 使用…...

【C++ 学习 ㉘】- 详解 C++11 的列表初始化
目录 一、C11 简介 二、列表初始化 2.1 - 统一初始化 2.2 - 列表初始化的使用细节 2.2.1 - 聚合类型的定义 2.2.2 - 注意事项 2.3 - initializer_list 2.3.1 - 基本使用 2.3.2 - 源码剖析 一、C11 简介 1998 年,C 标准委员会发布了第一版 C 标准࿰…...

OpenCV12-图像卷积
OpenCV12-图像卷积 图像卷积 图像卷积 OpenCV中提供了filt2D()函数用于实现图像和卷积模板之间的卷积运算: void filter2D(InputArray src, // 输入图像OutputArray dst, // 输出图像int ddepth, // 输出图像数据类型(深度)ÿ…...
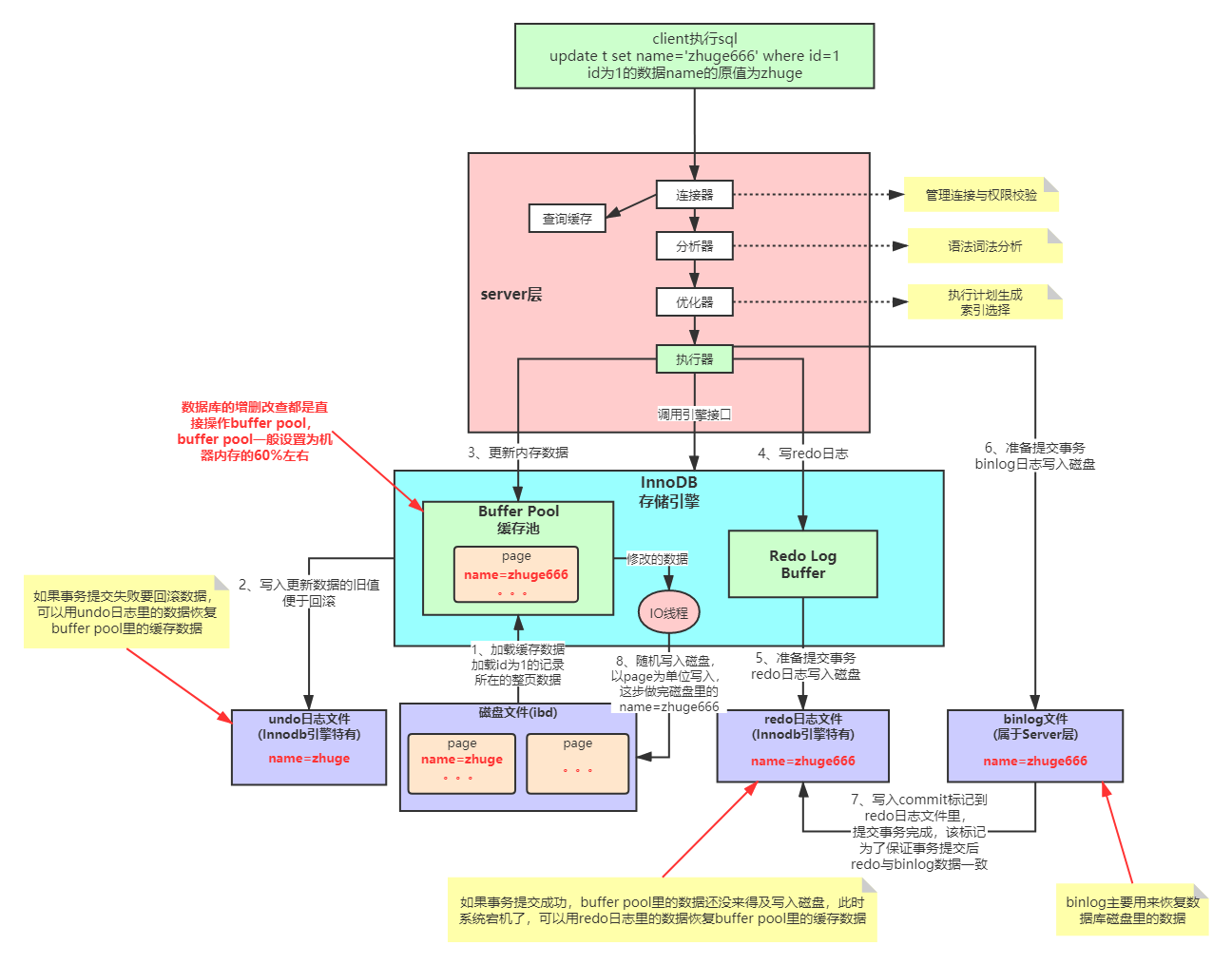
MVCC与BufferPool缓存机制
MVCC多版本并发控制机制 Mysql在可重复读隔离级别下如何保证事务较高的隔离性,我们上节课给大家演示过,同样的sql查询语句在一个事务里多次执行查询结果相同,就算其它事务对数据有修改也不会影响当前事务sql语句的查询结果。 这个隔离性就是…...
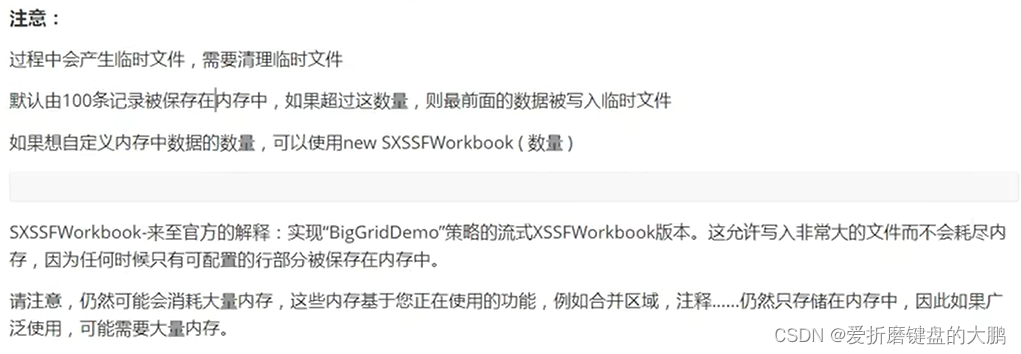
POI、Easy Excel操作Excel
文章目录 1.常用的场景2.基本功能3.Excel在Java中是一个对象4. 简单的写(07版本(.xlsx)Excel)大文件写HSSF大文件写XSSF大文件写SXSSF 5. Excel读5.1 读取遇到类型转化问题该怎么解决5.2 遇到Excel公式怎么办 6. Easy Excel6.1简单…...

网络安全(黑客)自学方向
每年报考网络安全专业的人数很多,但不少同学听说千万别学网络安全,害怕网络安全专业很难就业。下面就带大家深入了解一下网络安全专业毕业后可以干什么,包括网络安全专业的就业前景和方向等。 随着信息化时代的到来,网络安全行业…...

react写一个简单的3d滚轮picker组件
1. TreeDPicker.tsx文件 原理就不想赘述了, 想了解的话, 网址在: 使用vue写一个picker插件,使用3d滚轮的原理_vue3中支持3d picker选择器插件-CSDN博客 import React, { useEffect, useRef, Ref, useState } from "react"; import Animate from "../utils/an…...

Compose竖向列表LazyColumn
基础列表一 LazyColumn组件中用items加载数据,rememberLazyListState()结合rememberCoroutineScope()实现返回顶部。 /*** 基础列表一*/ Composable fun Items() {Box(modifier Modifier.fillMaxSize()) {val context LocalContext.currentval dataList arrayLi…...

6.自定义相机控制器
愿你出走半生,归来仍是少年! Cesium For Unity自带的Dynamic Camera,拥有优秀的动态展示效果,但是其对于场景的交互方式用起来不是很舒服。 通过模仿Cesium JS 的交互方式,实现在Unity中的交互: 通过鼠标左键拖拽实现场景平移通过…...
一文带你GO语言入门
什么是go语言? Go语言(又称Golang)是Google开发的一种静态强类型、编译型、并发型,并具有垃圾回收功能的编程语言。Go语言的主要特点包括:- 简洁和简单 - 语法简单明快,易于学习和使用 特点 高效 编译速度快,执行效率高 并发支持 原生支持并发,利用goroutine实现高效的并发…...

前后端小项目链接
1.vue的创建 vue的项目创建 1.1 vue create vue_name 1.2 Babel Router(路由) CSS Pre-processors 路由可通过:npm i vue-router3.5.2 -S 下载 1.3less 1.4 In dedicated config files 1.5 启动命令:npm run serve 端口号在vue.config。js中配置 devS…...
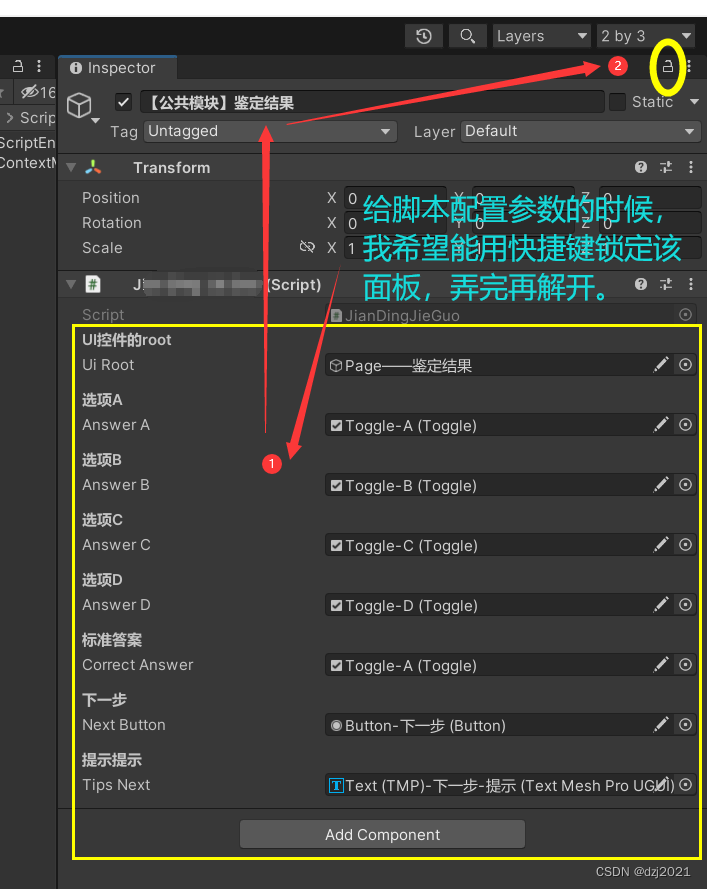
编辑器功能:用一个快捷键来【锁定】或【解开】Inspector面板
一、需求 我有一个脚本,上面暴露了许多参数,我要在场景中拖物体给它进行配置。 如果不锁定Inspector面板的话,每次点击物体后,Inspector的内容就是刚点击的物体的内容,而不是挂载脚本的参数面板。 二、 解决 &…...

Vue 网络处理 - axios 异步请求的使用,请求响应拦截器(最佳实践)
目录 一、axiox 1.1、axios 简介 1.2、axios 基本使用 1.2.1、下载核心 js 文件. 1.2.2、发送 GET 异步请求 1.2.3、发送 POST 异步请求 1.2.4、发送 GET、POST 请求最佳实践 1.3、请求响应拦截器 1.3.1、拦截器解释 1.3.2、请求拦截器的使用 1.3.3、响应拦截器的使…...
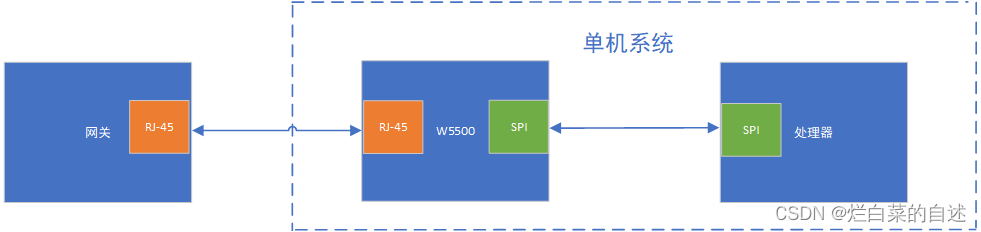
关于W5500网卡使用过程的部分问题记录
某个项目中用到了W5500这种自带网络协议栈的网卡芯片,由于该项目开发时间很紧,就临时网上买了一些模块拼凑到了一套系统,经过验证果真这种拼积木的方法只能用在学生实验开发中,真不能拿来做工程应用,硬件太不稳定很容易…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...