【算法设计与分析zxd】第7章 贪心法
贪心算法的设计技术
用贪心法 求问题的解
【例7-1】
问题分析
命题:
那么B是S’的一个最优解。若不然,假如S’有解B’,B’>B,那么用B’替换B以后得到解{i1 ,i2 , …,ik}∪B’,将比S的活动更多,这与S是最优解矛题得证。
计算模型
struct Active{startTime s;//开始时间endTime e;//结束时间selectflag f;//选标识
}A[n];(2)计算:
活动i 与 活动j 相容 -> A[ i ].s >= A[ j ].e 或 A[ j ].s >= A[ i ].e
用归并排序 或 其他任何高效的排序算法完成 以a[i].e的从小到大 的排序,形成排序A[1].e≤A[2].e ≤…≤A[n].e
【例7-2】数列极差。
问题分析
命题:
证明:
(1) 当k=3时,
数列a={a1 , a2 , a3},不妨令a1< a2< a3 ,这样
——思考:
A={a1,a2},B={b1,b2,b3}, 设[A]=[a1 a2]=a1*a2+1 一种值在运算中{B}={b1,b2,b3}表示三个 顺序 ,即[b1 b2 b3], [b1 b3 b2], [b2 b3 b1],若有A<a3<B<a4, 试比较 [[A],a3,{B},a4]与 [[A],a4,{B},a3]猜测:[[A],a3,{B},a4] > [[A],a4,{B},a3]
因为a3<a4 ,设a4=a3+k , a3=a4-k
[[A],a3,{B},a4]
=[ [A] ,a4-k ,{B} ,a4 ]
= [ [A]*(a4-k)+1 , {B},a4 ]
=[ [ A,a4]-[A]*k ,{B},a4 ] ——(1)B={b1,b2,b3} 取任意一个次序
[[A],a3,{B},a4] ——代入(1)式
=[ [A,a4]-[A]*k ,{ b1, b2,b3,b4},a4 ]
=[ [A,a4]-[A]*k ,b1, {b2,b3,b4},a4 ]
= [ ( [A,a4]-[A]*k )*b1+1 , {b2,b3,b4},a4 ]
=[ [A,a4,b1] -[A]*k*b1 , {b2,b3,b4},a4 ]
=.....
= [ [A,a4,b1,b2,b3]-[A]*k*b1*b2*b3 ,a4 ]
=[ [A,a4,b1,b2,b3] *a4 -[A]*k*b1*b2*b3*a4 +1]
=[ [A,a4,b1,b2,b3] *a4 +1 -[A]*k*b1*b2*b3*a4 ]从结果倒推,找[[A],a4,{B},a3] 形式
aj=ai+k ,a4=a3+k ,
[[A],a3,{B},a4]
=[ [A,a4,b1,b2,b3] *a4 +1 -[A]*k*b1*b2*b3*a4 ] (上文,代入a4=a3+k)
=[ [A,a4,b1,b2,b3] *(a3+k) +1 -[A]*k*b1*b2*b3*a4 ]
=[ [A,a4,b1,b2,b3] *a3+[A,a4,b1,b2,b3]*k +1 -[A]*k*b1*b2*b3*a4 ]
=[ [A,a4,b1,b2,b3,a3]+[A,a4,b1,b2,b3]*k -[A]*k*b1*b2*b3*a4 ]
=[ [A,a4,b1,b2,b3,a3]+k*( [A,a4,b1,b2,b3] -[A]*b1*b2*b3*a4 ) ]
= [ [A,a4,B,a3+k] +1 - [A]*k*b1*b2*b3*a4 ]
=[ [A,a4,B] *(a3+k)+1 - [A]*k*b1*b2*b3*a4 ]
=[ [A,a4,B] *a3+1+[A,a4,B] *k - [A]*k*b1*b2*b3*a4 ]
=[ [A,a4,B,a3] + [A,a4,B] *k - [A]*k*b1*b2*b3*a4 ]
= [ [A,a4,B,a3] + k* ( [A,a4,B] - [A]*b1*b2*b3*a4 ) ]
只需比较 [A,a4,B] - [A]*b1*b2*b3*a4 与0
( [A]*a4 +1 )*B+1 -[A]*b1*b2*b3*a4
=展开或者非常显然 >0因此[[A],a3,{B},a4] > [[A],a4,{B},a3]
设A={a1,a2...an}
[A,ai]
= [{a1,a2,...an} ,ai ]
=[a1,a2,a3...an,ai]
=[ a1*a2+1,a3...an,ai]
=[ ((a1*a2)+1 )*a3+1,....an,ai]
=[ [A],ai ]
(2)假设k=n时命题成立。
——引理
设有数列集合A和B,正整数a i , a j ,且有A<a i < a j <B,其中,B={b 1 , b 2 , …b m },{B}表示B中元素的任意组合序列,则有[ [A] , a i , {B}, a j ]> [ [A], a j , {B}, a i ]。引理证明:第一个表达式 用第二个表达的出来,比较差别
∵ai< aj,∵不妨设aj = ai +k, ai = aj – k // (k>0)
ai = aj – k
[[A], ai, {B}, aj]
= [[A], aj – k, {B}, aj]
= [[A]*(aj – k)+1, {B}, aj]
= [[A]*aj –[A]*k+1, {B}, aj] = [ [A]*aj+1 – [A]*k, {B}, aj]
=[ [A, aj] –[A]*k, {B}, aj]将B={b1 , b2 , …bm }代入上式,并取B的[任意]一个次序
[[A], ai, B, aj]
= [[A, aj] –[A]*k, b1 ,{ b2 , …bm}, aj]
= [([A, aj] –[A]*k)*b1 +1,{ b2 , …bm}, aj]
=[ [A, aj] *b1 –[A]*k*b1 +1,{ b2 , …bm}, aj]
= [ [A, aj,b1 ] –[A]*k*b1 ,{ b2 , …bm}, aj]
= [ [A, aj,b1 ,b2 ,…bm] –[A]*k*b1 * b2 *…*bm, aj]
= [ ([A, aj,b1 ,b2 ,…bm]–[A]*k*b1 * b2 *…*bm) * aj +1]
= [ [A, aj,b1 ,b2 ,…bm] * aj–[A]*k*b1 * b2 *…*bm* aj +1]代入aj = ai +k,B= b1,b2,…bm
[[A], ai, B, aj]
= [ [A, aj, B] * (ai+k)+1 –[A]*k*b1* b2*…*bm* aj]
= [ [A, aj, B] * ai+1+[A, aj, B] *k –[A]*k*b1* b2*…*bm* aj]
= [ [A, aj, B, ai] +[A, aj, B] *k –[A]*k*b1* b2*…*bm* aj]
= [ [A, aj, B, ai] + k * ([A, aj, B] –[A]*b1* b2*…*bm* aj)]
//证明+的这个 k * ([A, aj, B] –[A]*b1* b2*…*bm* aj)]>0依据B次序的任意性,可得[[A], a i ,{B}, a j ] = [ [A, a j , {B}, a i ] + k * ([A, a j , B] –[A]*b 1 * b 2 *…*b m * a j )]因为[A, a j]=[A]* aj +1,所以[A, a j, B] >[A]*b1 * b2 *…*bm* a j ,//[ A aj B ]= ( [ A ]*aj +1 )*B+1 =[ A ] * aj*B +B +1则必定有 [[A], a i ,{B}, a j ] > [A, a j , {B}, a i ]∴引理成立。引理推广[{A}, a i ,{B}, a j ] > [{A}, a j , {B}, a i ] 当 [{A}]<a i < a j <[{B}]A的任意顺序引理:[ [A] , ai, {B}, aj ]> [ [A], aj, {B}, ai ]。
根据计算可以得出 [A , ai ] = [ [A], ai ]
但是[ai,A] != [ai,[A] ]
比如[ai ,a1,a2]= (ai*a1+1)*a2+1 =ai*a1*a2+ai*a1+a2+1
[ai,[A]]=ai*(a1*a2+1)=ai*a1*a2+ai

计算模型
代码:
#include<bits/stdc++.h>
using namespace std;
//堆排序 -完全二叉树
/*01 23 4 5 6
*/void show(int a[],int n)
{for(int i=0;i<n;i++){cout<<a[i]<<"\t";}cout<<endl<<endl;
}void min_h(int a[],int start,int end)
{//建立父节点指针和子节点指针int f=start;///父节点 int c=f*2+1;//左孩子 int t;//用于交换的临时变量 while(c<=end)//若子节点指针在范围内,进行比较 {//找到最小值的下标 if(c+1<=end && a[c]>a[c+1])//右孩子在范围中,左孩子>右孩子 {c++;}//选中左右孩纸中较小值 //如果父节点 < 子节点 //此时 父<右<左 调整完成 if(a[f]<a[c])return;else//交换 父>右 左>右 ,右是最小的 换到父节点上去 {t=a[f];a[f]=a[c];a[c]=t;f=c;c=f*2+1;}}
}
void min(int a[],int n)
{//初始化 i从最后一个父节点开始调整for(int i=n/2-1;i>=0;i--){min_h(a,i,n-1);} for(int i=n-1;i>0;i--){swap(a[0],a[i]);min_h(a,0,i-1);}
}
int cal(int a[], int n)
{int v1=0,v2=1;while (n > 2){show(a,n);min(a, n);//maxa[v1] = a[v1] * a[v2] + 1;a[v2] = a[n-1];//下次还需排序,因此不用在意顺序,直接将最后一个向前移动n = n - 1;//数目--}//此时n==2return a[0] * a[1] + 1;
}
int main()
{int n = 4;int a[4] = { 8,2,1,3 };cout<<"最大极差:" << cal(a, n);return 0;
}
【例7-3】最优装载。
问题分析
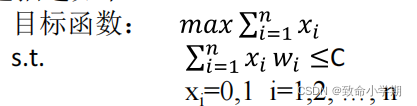
贪心策略:轻者优先
| 算法设计与描述 | 算法分析 |
| 输入: | (1)问题输入规模为n |
| 输出: | |
| (2)选择集装箱是主要工作,时间渐进复杂度T(n)=n (3)排序最快的时间复杂度T(n)=O(nlogn) (4)上述(2)(3)是并列执行的,按照第2章的定理2.2可知时间渐进复杂度T(n)=O(nlogn) |
t[]数组存放集装箱的原始编号。通过t 找到x 下标变量
【例7-4】键盘输入
n1=“1 2 4 3 5 8 6 3”n2=“2 3 1 1 8 3 1”n3=“1 2 3 4 5 6 7”n4=“1 2 0 0 8 3”=》n1=“1 2 3 5 3”n2=“2 1 1 1” 应该是1131 需要回溯,只需向上回溯一位n3=“1 2 3 4 5 6 7” 应该直接划掉后三个 没删除, 有木有n4=“1 0 0 3” 没删够, 有木有
计算模型
代码:
#include<bits/stdc++.h>
using namespace std;int n = 6;//长度
int s = 3;//要删除的数字个数
char a[] = { '1','2','0','0','8','3' };//数字
int data[3] = { 0 };//记录删除的元素在原数字中的位置 void show(char a[])
{for(int i=0;i<strlen(a);i++)cout<<a[i]<<'\t';cout<<endl;
}
void del(char a[], int b, int k)//删除,物理覆盖
{for (int i = b; i < strlen(a); i++){a[i] = a[i + k];}
}
void delD(char a[], int s)
{int i = 0, j = 0, j1 = -1;//存在回溯 int len = strlen(a);//截止到\owhile (i < s && j < strlen(a)){show(a);while (a[j] <= a[j + 1])//一直是前面小 {j++;}//前面大于后面if (j < strlen(a)){//删除a[j]del(a, j, 1);//删除次数 i if (j >= j1)data[i] = j + i;//删除的第i个元素,在原数组中的位置是j+i else data[i] = data[i - 1] - 1;//回溯,回溯到上一个删除位置 的前一个位置 //j1 = j;i++;j--;if (j < 0)j = 0;}}//显示的时候高位的0不显示 while (a[0] == '0' && strlen(a)) del(a, 0, 1);}int main()
{delD(a, s);cout<<"位置"<<endl;for(int i=0;i<s;i++){cout<<data[i]<<"\t";}cout<<endl<<"新整数";for (int i = 0; i < n-s; i++)cout << a[i];return 0;
} 近似贪心问题
相关文章:
【算法设计与分析zxd】第7章 贪心法
贪心算法的设计技术 • 每一步的判断都是一个当前最优的抉择,这个抉择计算设计的好坏,决定了算法的成败。 • 多步判断过程,最终的判断序列对应于问题的最优解 • 适用于 能够 由 局部最优达到全局最优的优化问题 【比如 求最短哈密顿回路的…...

CCF CSP认证 历年题目自练Day35
题目一 试题编号: 202305-1 试题名称: 重复局面 时间限制: 1.0s 内存限制: 512.0MB 问题描述: 题目背景 国际象棋在对局时,同一局面连续或间断出现3次或3次以上,可由任意一方提出和棋。 问题…...

应用crash时发送广播及信息
一、环境 高通865 Android 10 二、情景 应用崩溃时,将奔溃信息以广播的形式发送 二、代码位置 frameworks/base/core/java/com/android/internal/os/RuntimeInit.java private static class KillApplicationHandler implements Thread.UncaughtExceptionHandle…...

【亲测可用】图像目标识别入门-利用笔记本电脑摄像头识别人脸标记出来采用深度学习模型实现
更高的精度和准确性,可以考虑使用基于深度学习的人脸检测和识别方法,例如基于人脸特征的人脸检测器和具有高识别率的人脸识别模型。下面是使用基于深度学习的人脸检测和识别方法的代码示例: 首先,安装必要的库和模型:…...
数字孪生技术:煤矿运输的未来革命
煤矿是我国能源工业的重要支柱,然而,煤矿运输过程中一直存在着诸多问题,如安全隐患、能源浪费、效率低下等,这不仅对煤矿行业的可持续发展构成威胁,也对环境造成负面影响。因此,数字孪生技术应运而生&#…...
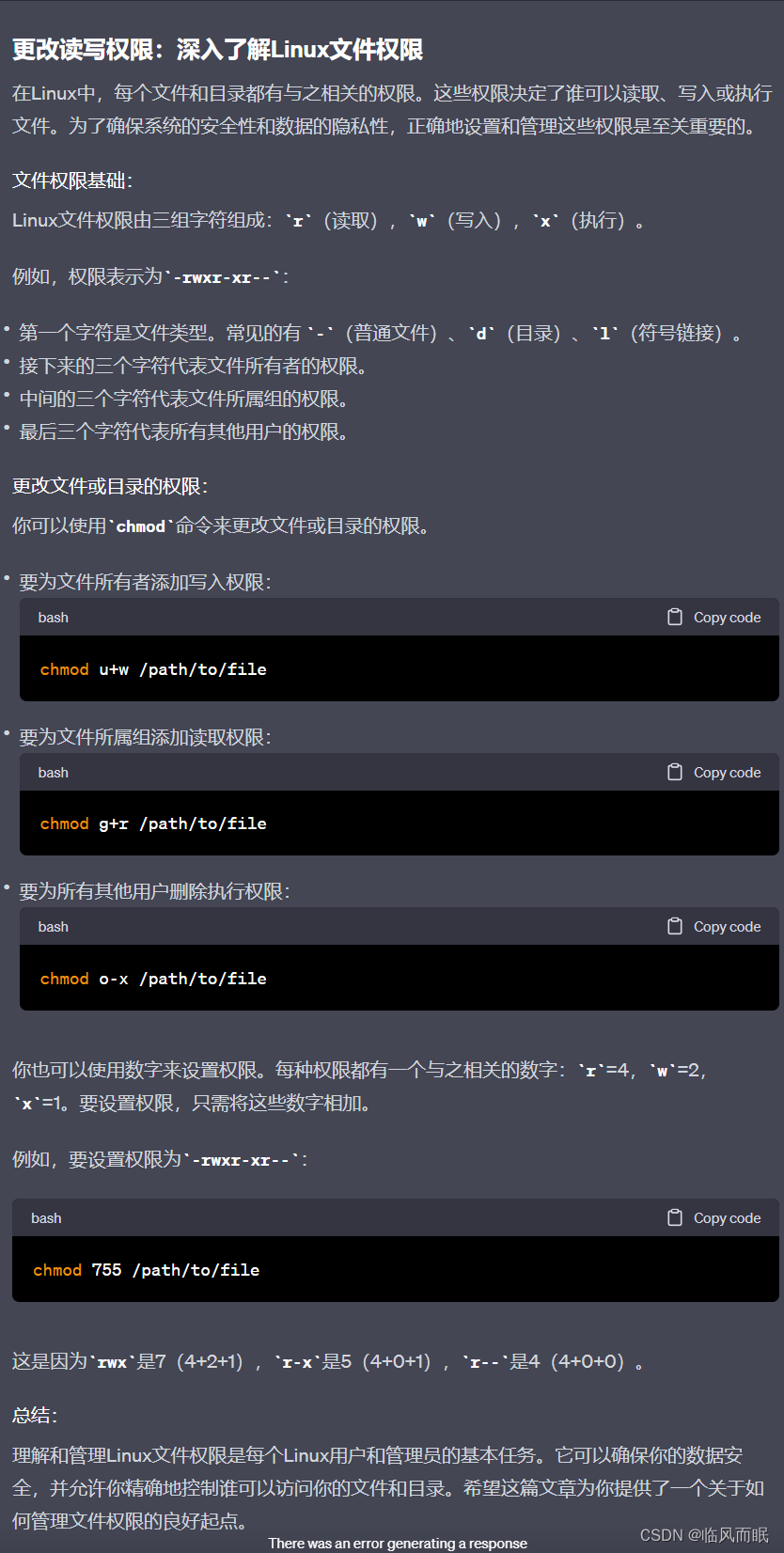
一些bug总结
今天被几个小问题和bug折磨了一天,来总结一下… 权限问题 用vscode连接服务器,如果是在root用户连接的情况下新建的文件/文件夹,然后切换到别的用户的时候去写的代码 可能会遇到各种问题 解决方案是更改文件或文件夹的所有权。这可以通过使用…...

第三章 内存管理 九、基本分段存储管理方式
目录 一、概括 二、什么是分段 三、段表 四、地址转换 五、分段和分页的对比 六、总结 一、概括 基本分段存储管理方式是一种操作系统的内存管理方式,采用这种方式,将进程所需的内存分成若干个段,每个段都可以单独进行管理和保护。 具…...

轻重链剖分+启发式合并专题
Codeforces-741D(Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths) 一棵根为1 的树,每条边上有一个字符(a-v共22种)。 一条简单路径被称为Dokhtar-kosh当且仅当路径上的字符经过重新排序后可以变成一个回文串。 求每个子树中…...
、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略)
IRC/ML:金融智能风控—信贷风控场景简介、两大场景(贷款场景+信用卡场景)、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略
IRC/ML:金融智能风控—信贷风控场景简介、两大场景(贷款场景+信用卡场景)、信用卡评分模型设计、反欺诈检测技术的简介、案例应用之详细攻略 目录 信贷风控简介 信贷风控两大场景...
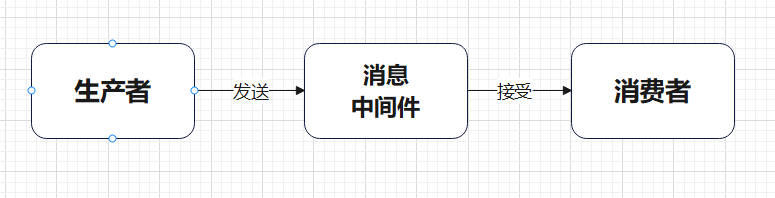
【学习笔记】RabbitMQ01:基础概念认识以及快速部署
参考资料 RabbitMQ官方网站RabbitMQ官方文档噼咔噼咔-动力节点教程 文章目录 一、认识RabbitMQ1.1 消息中间件(MQ Message Queue 消息队列1.2 主流的消息中间件1.3 MQ的应用场景1.3.1 异步处理1.3.2 系统解耦1.3.3 流量削峰1.3.4 日志处理 二、RabbitMQ运行环境搭建…...

Java数据结构之第二十章、手撕平衡AVL树
目录 一、二叉平衡树 1.1二叉搜索树回顾以及性能分析 1.1.1二叉搜索树的概念 1.2二叉搜索树的查找 1.3二叉树查询性能分析 二、AVL树 2.1AVL树的概念 2.2AVL树节点的定义 2.3AVL树的插入 2.4AVL树的旋转 2.4.1新节点插入较高左子树的左侧---右单旋 2.4.2新节点插入较…...

SQL 在PostgreSQL中使用SQL将多行连接成数组
在本文中,我们将介绍如何使用SQL语言在PostgreSQL数据库中将多行数据连接成一个数组。在开发和分析应用程序时,我们经常需要将数据库中的多个行合并为一个,以便更方便地进行处理和分析。PostgreSQL提供了一种名为ARRAY_AGG的聚合函数…...

Ajax技术实现前端开发
一、原生AJAX 1.1AJAX 简介 AJAX 全称为Asynchronous JavaScript And XML,就是异步的JS 和XML。 通过AJAX 可以在浏览器中向服务器发送异步请求,最大的优势:无刷新获取数据。 AJAX 不是新的编程语言,而是一种将现有的标准组合在一起使用的新方式。 1.2XML 简介 XML 可扩…...

WebMail:网页注册成功发送邮件
1.特别注意 isELIgnored"false" 如果没有这个El表达式无法识别 2.pre work pox.xml <dependencies><dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>3.8.1</version><scope>…...
Electron之集成vue+vite开发桌面程序
在electron中集成vue开发桌面程序 使用我们之前创建的electron项目 创建vue 项目 命令行进入electron根目录 执行下面命令 npm create vitelatest vue -- --template vue这样就创建了一个vue项目,文件名是vue,命令行进入vue下,执行下面命…...

pycharm社区版创建Django项目的一种方式
pycharm社区版创建Django项目 pycharm创建New project安装django,如果安装过可略过安装完成后查看安装情况生成Django项目需要的文件这里注意生成语句后面的 . 不可以省略 生成文件后,框架搭建完成,配置启动我这里在配置完后,报了…...
Python configparser模块使用教程
文章目录 .ini 拓展名文件简介.ini 文件格式1. 节2. 参数3. 注解 configparser 模块简介configparser 模块的初始化和读取获取 ini 中所有 section获取 section 下的 key获取 section 下的 value获取指点section的所用配置信息修改某个key,如果不存在则会出创建检查…...

Kotlin + 协程 + Room 结合使用
文章目录 前言集成Room结合协程的使用总结 一、前言, 现在kotlin 是趋势,那必然就要用到协程,还有就是随着jetpack 的发力,带来了很多好用的库,比如今天提到Room,是一个类似greenDao的数据库。它不但支持kotlin协程…...
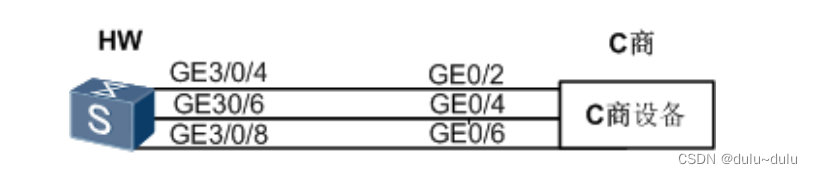
网工记背命令(6)----链路聚合配置
目录 1.配置手工负载分担模式链路聚合 2.配置LACP模式的链路聚合 3.HUAWEI设备与C厂商设备对接 链路聚合(Link Aggregation)是将多条物理链路捆绑在一起成为一条逻辑链路,从而增加链路带 宽的技术。 常用配置命令 1、执行命令 interface …...

使用 Service 把前端连接到后端
使用 Service 把前端连接到后端 如何创建前端(Frontend)微服务和后端(Backend)微服务。后端微服务是一个 hello 欢迎程序。 前端通过 nginx 和一个 Kubernetes 服务暴露后端所提供的服务。 使用部署对象(Deployment ob…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
