当前位置： 首页 > news >正文

数据结构--B树

news 文章来源：https://blog.csdn.net/m0_61402375/article/details/133905828 2025/5/25 9:16:01

目录

回顾二叉查找树

如何保证查找效率

B树的定义

提炼

B树的插入和删除

概括B树的插入方法如下

 B树的删除

导致删除时，结点不满足关键字的个数范围时（需要借）

如果兄弟不够借，需要合体

回顾B树的删除

B+树

B+树的查找

回顾B+树

B+树与B树对比

回顾二叉查找树

                          --能不能变成m叉查找树呢？

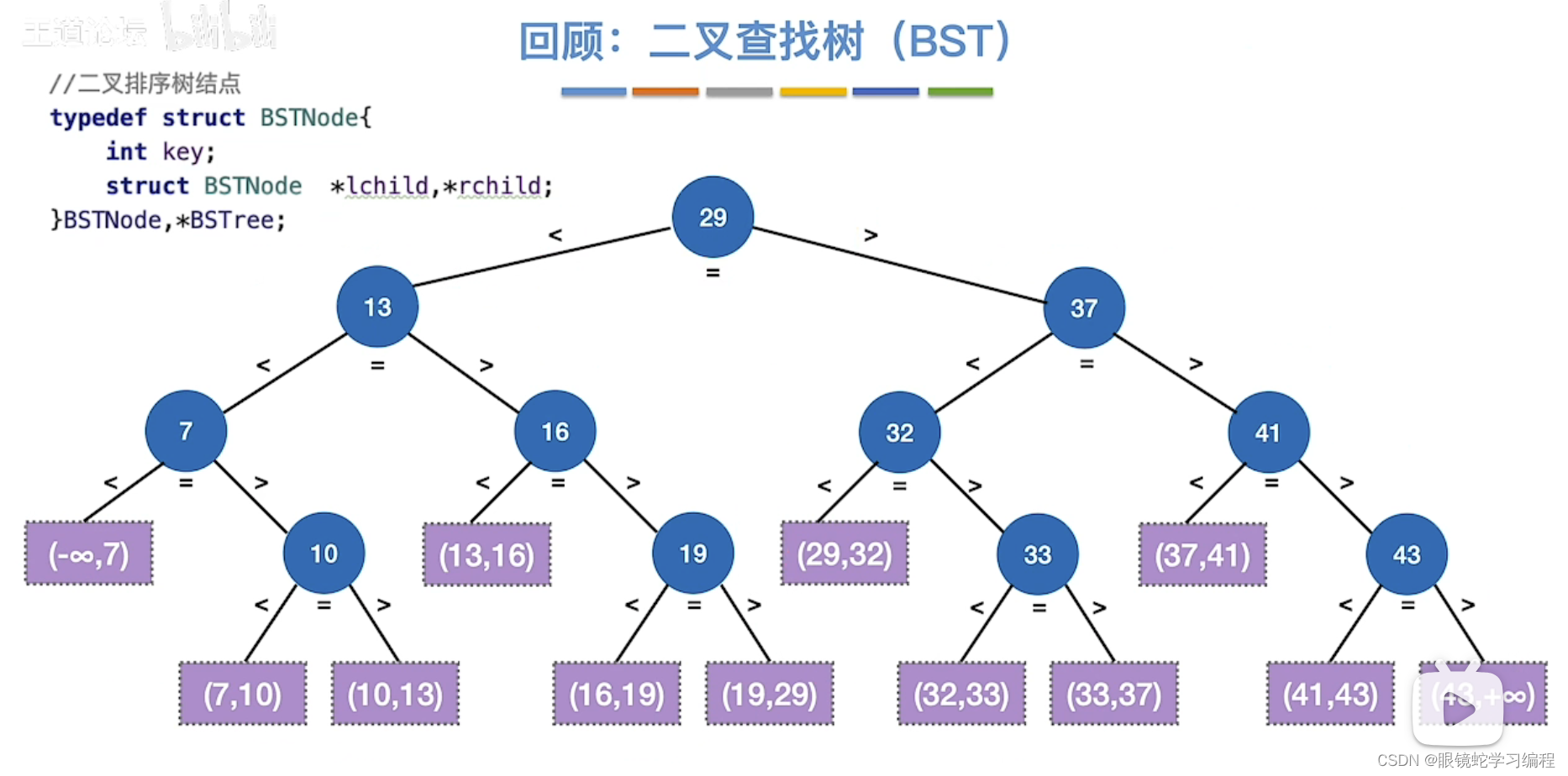
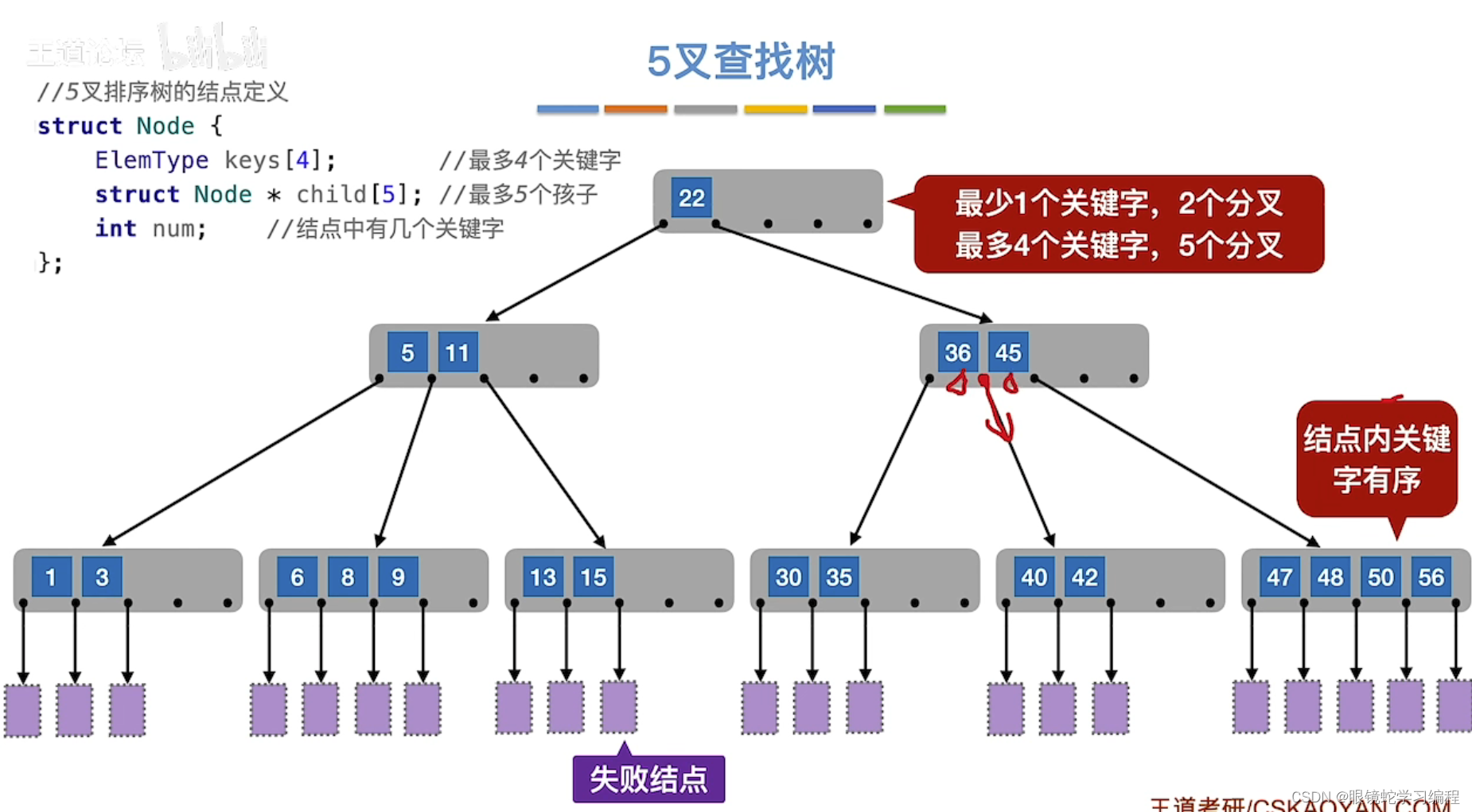
比如5叉查找树

紫色的是失败结点，每个子树内关键字结点都是有序的

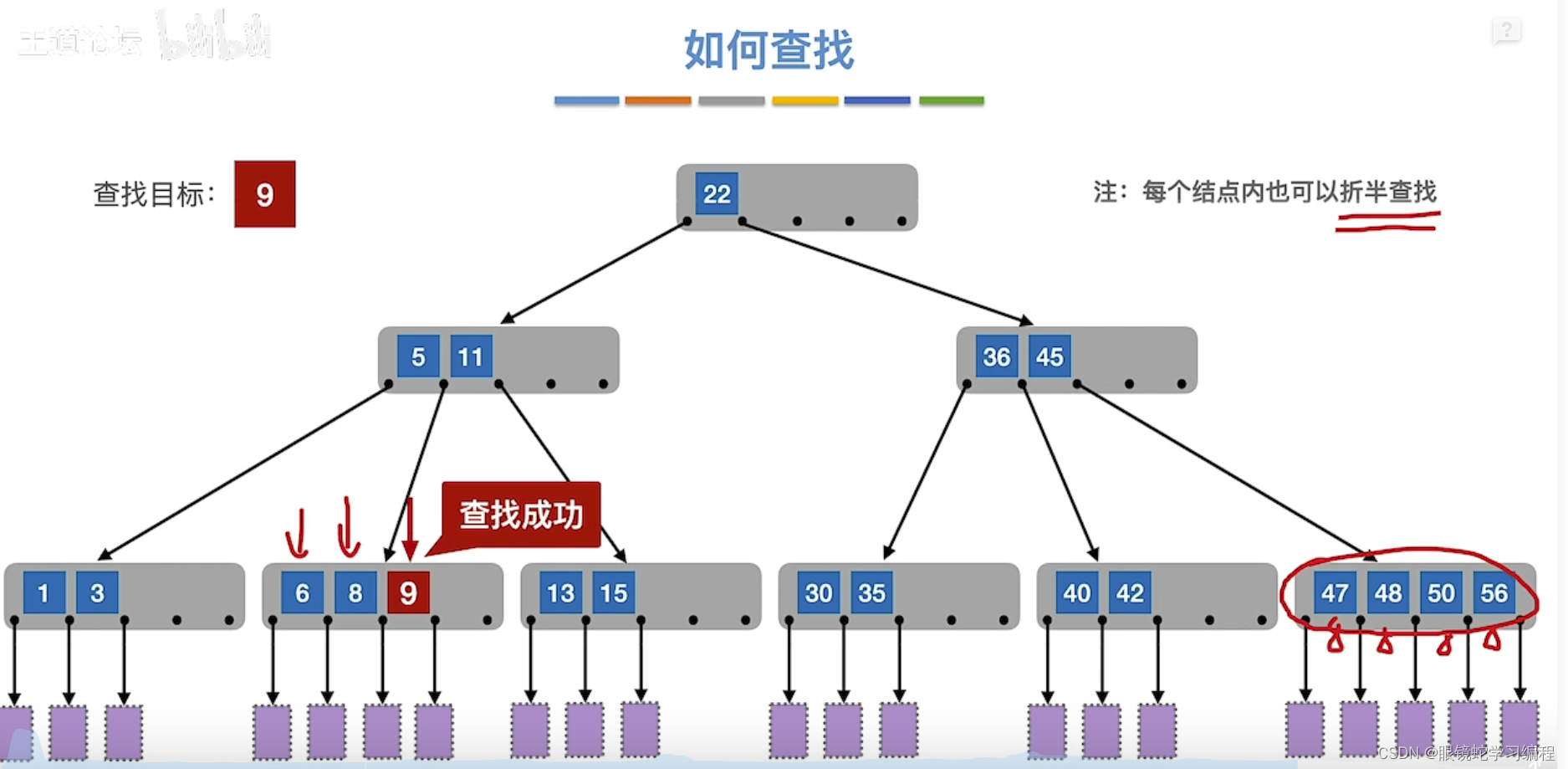
比如查找目标是9（查找成功的情况）

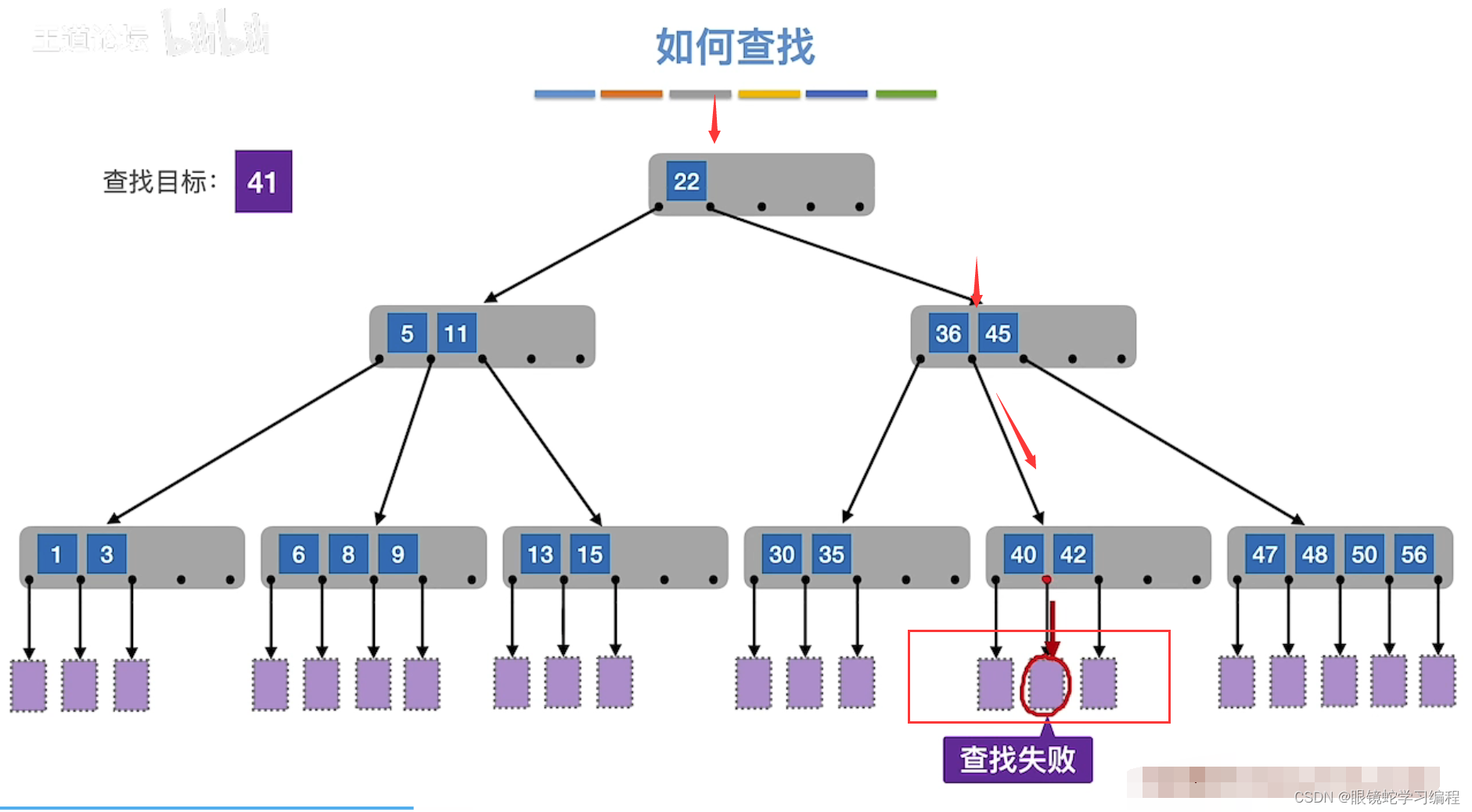
比如查找目标是（查找失败的情况）

对于查找失败就是最后找到的是NULL

如何保证查找效率

策略：m叉查找树，除了根节点外，任何结点至少有 m/2 （向上取整）个分叉，即至少有m/2（向上取整）-1个关键字

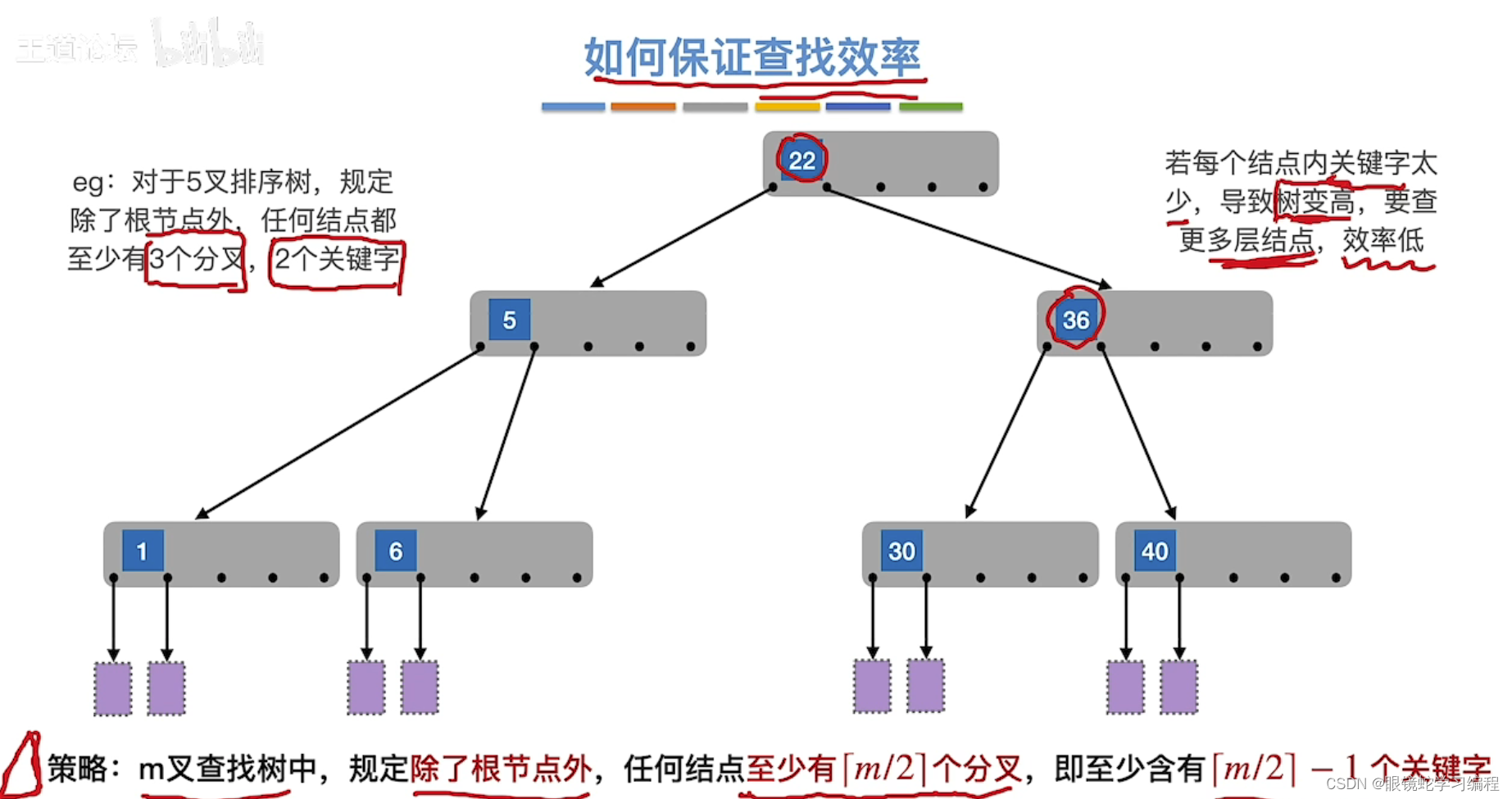
为什么要除了根节点呢？原因如下:

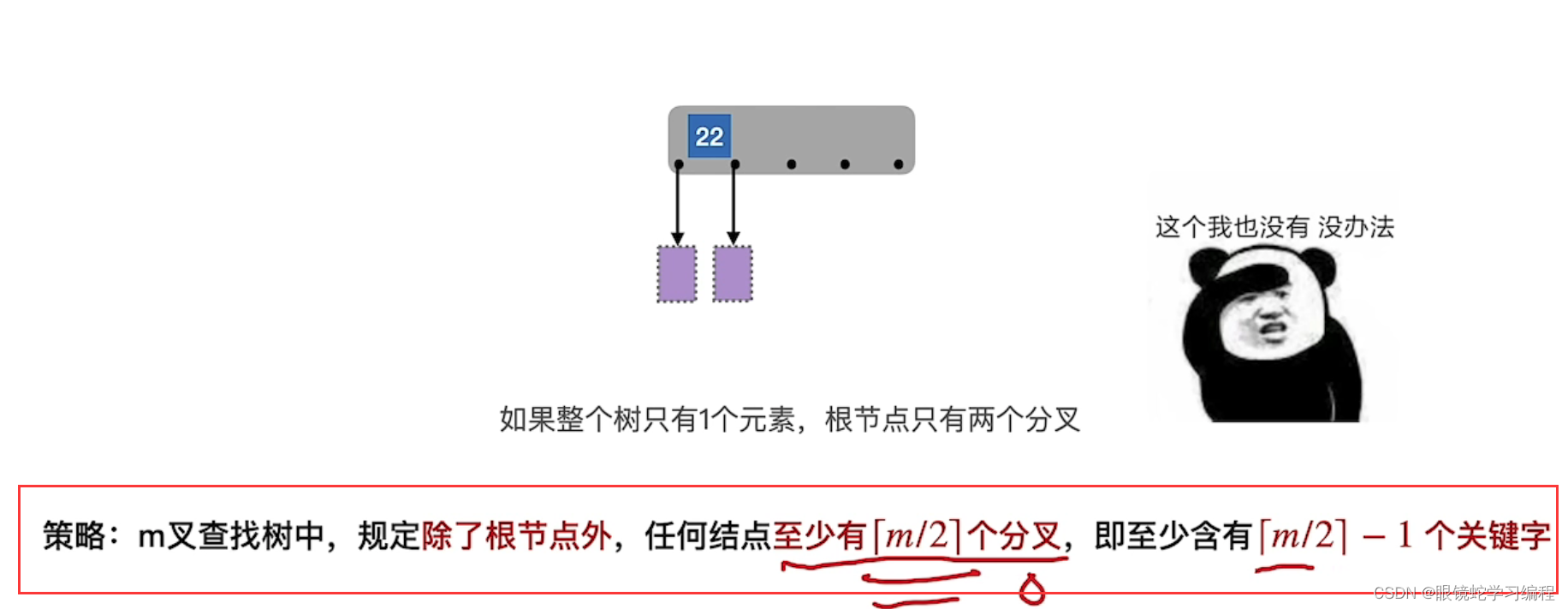
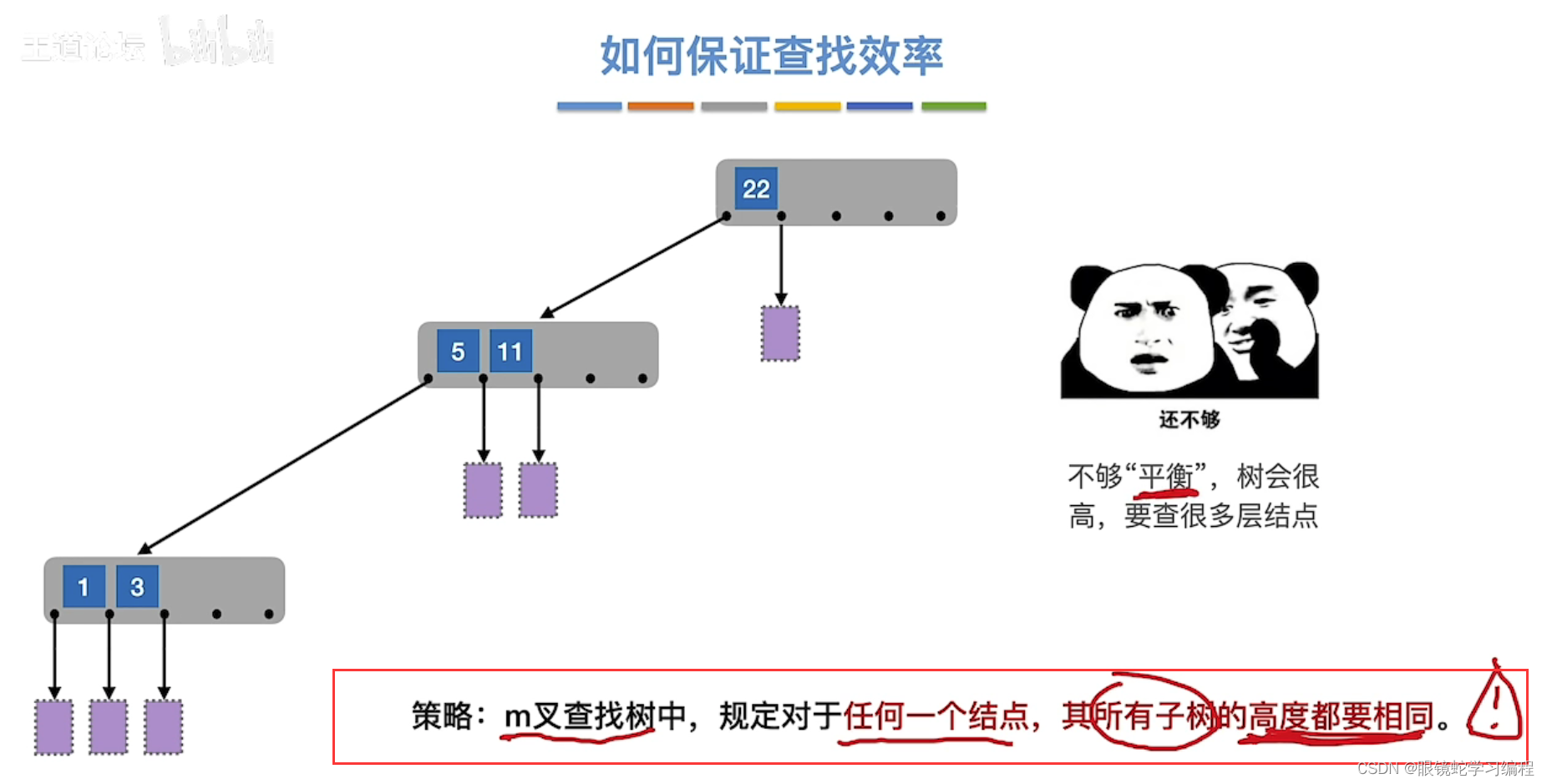
所以如果可以规定一个下限，（1）分叉不是特别少，（2）同时高度都要相同（即绝对平衡）

满足这两个条件那么就是一颗B树

如下图就是一颗5叉的B树

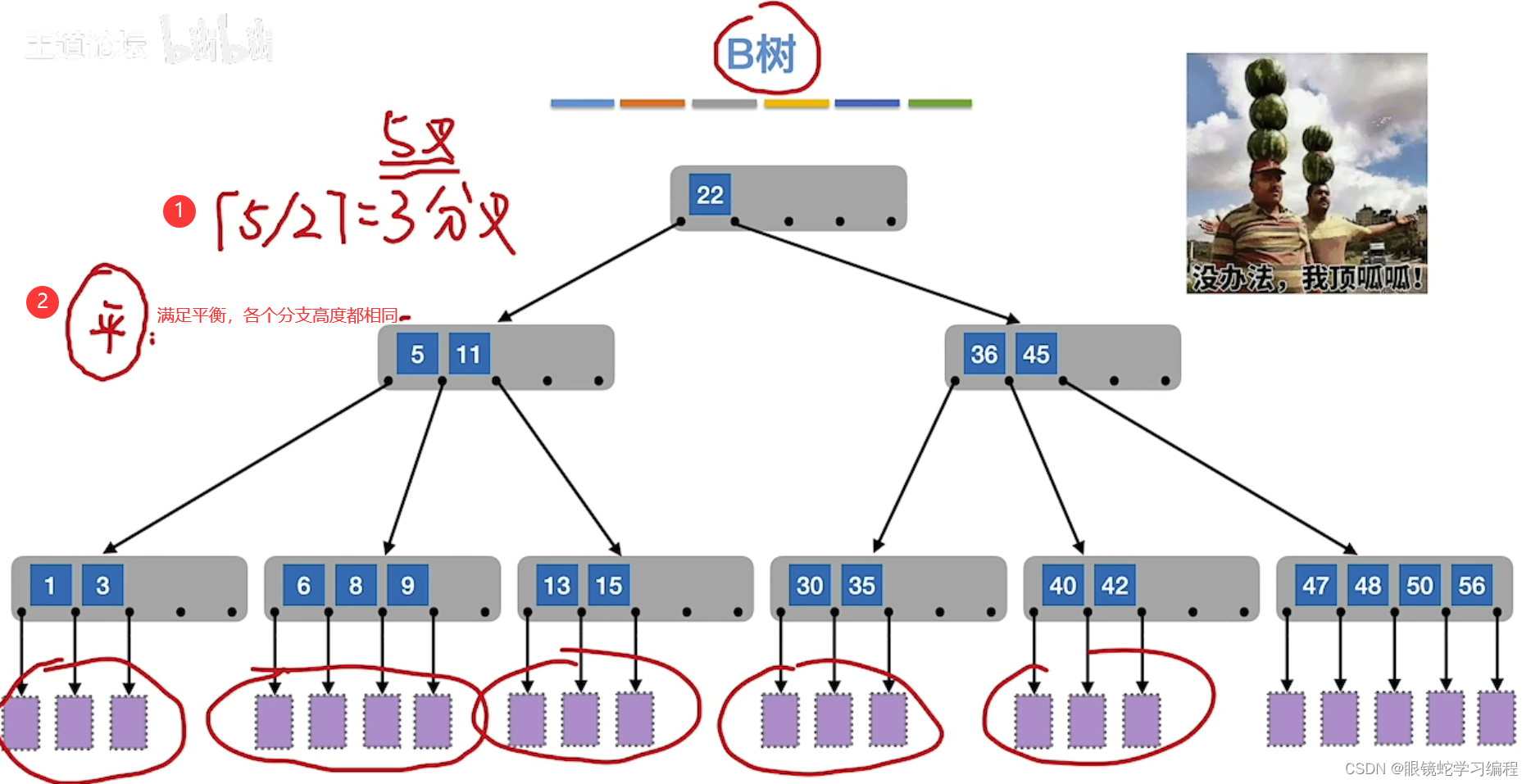
接下来是时候展示B树的定义了！！！！！！！！

B树的定义

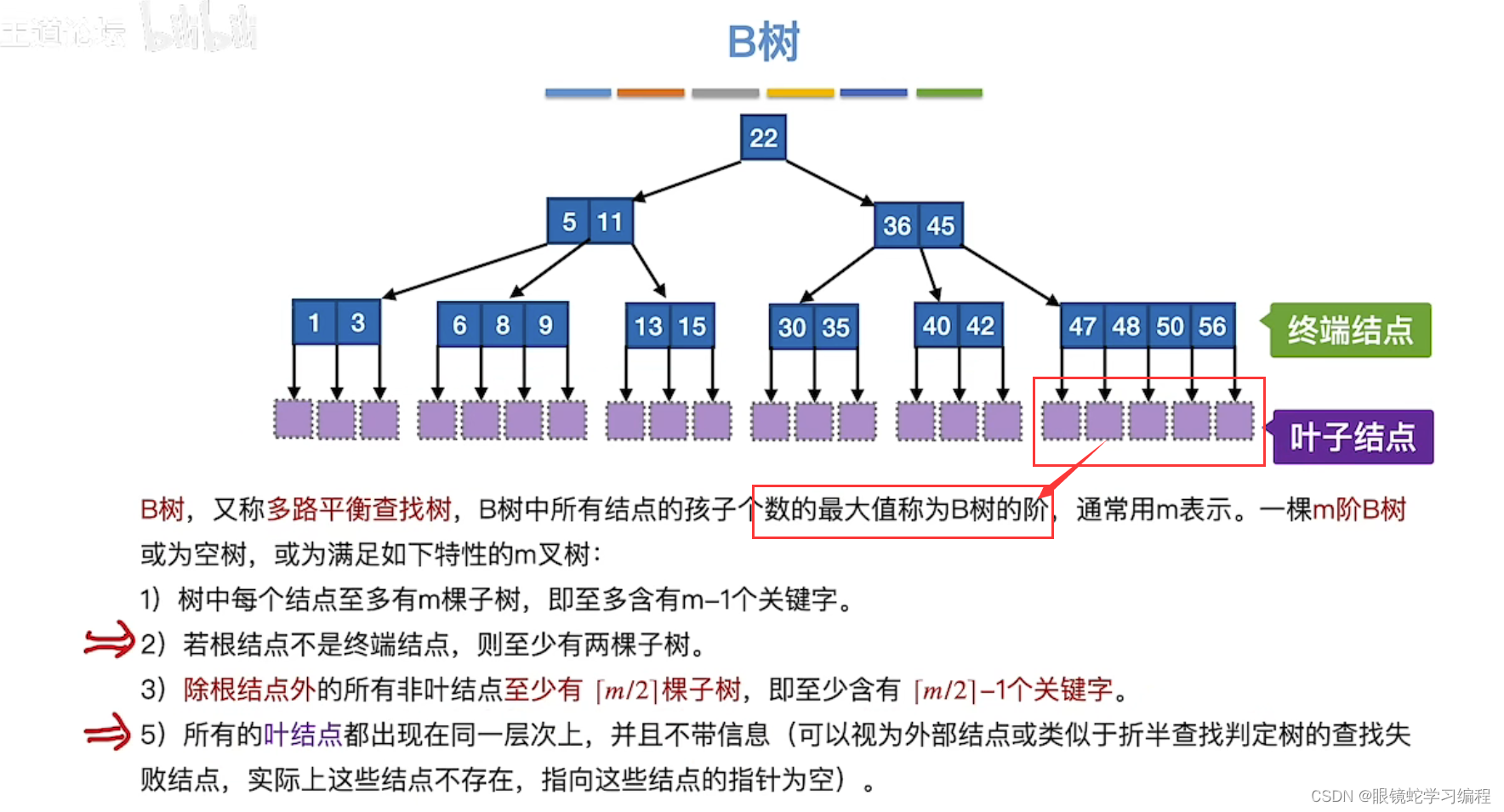
提炼

（自己可以容易理解的整理）

绝对平衡，是没有高度差的

终端结点：包含信息

叶子结点（本质就是失败节点，它是个空指针）：不包含信息

分叉个数最多的就是阶，图中分叉最多是5个，所以是5阶

2）若根节点不是终端结点，则至少有两颗子树的原因：是保证绝对平衡，没有高度差

5）所有叶结点都出现在同一层原因：是保证绝对平衡，没有高度差

4)K是关键字，P是指针，n是记录实际关键字到底有几个；K1<K2<....Kn是说关键字必须有序(这里是递增，也可以递减，只要有序即可)

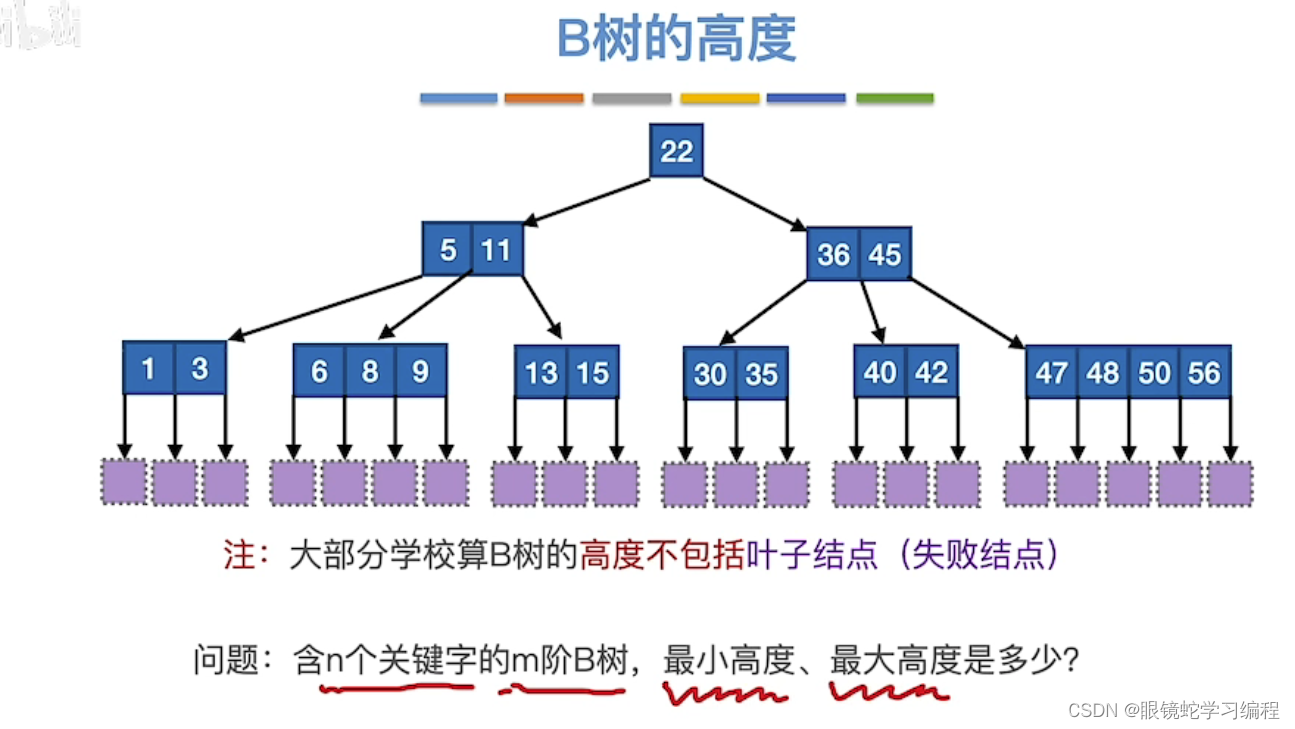
最小高度的计算

最大高度的计算

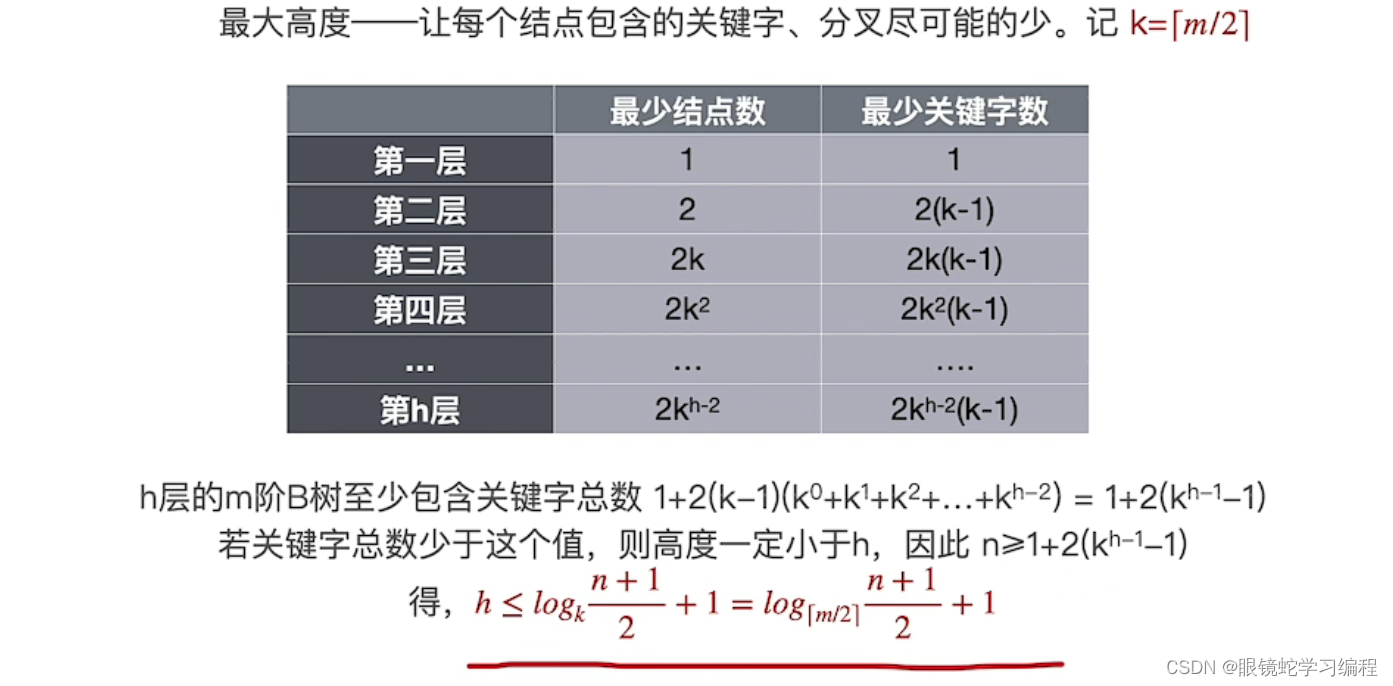
B树的本节总结

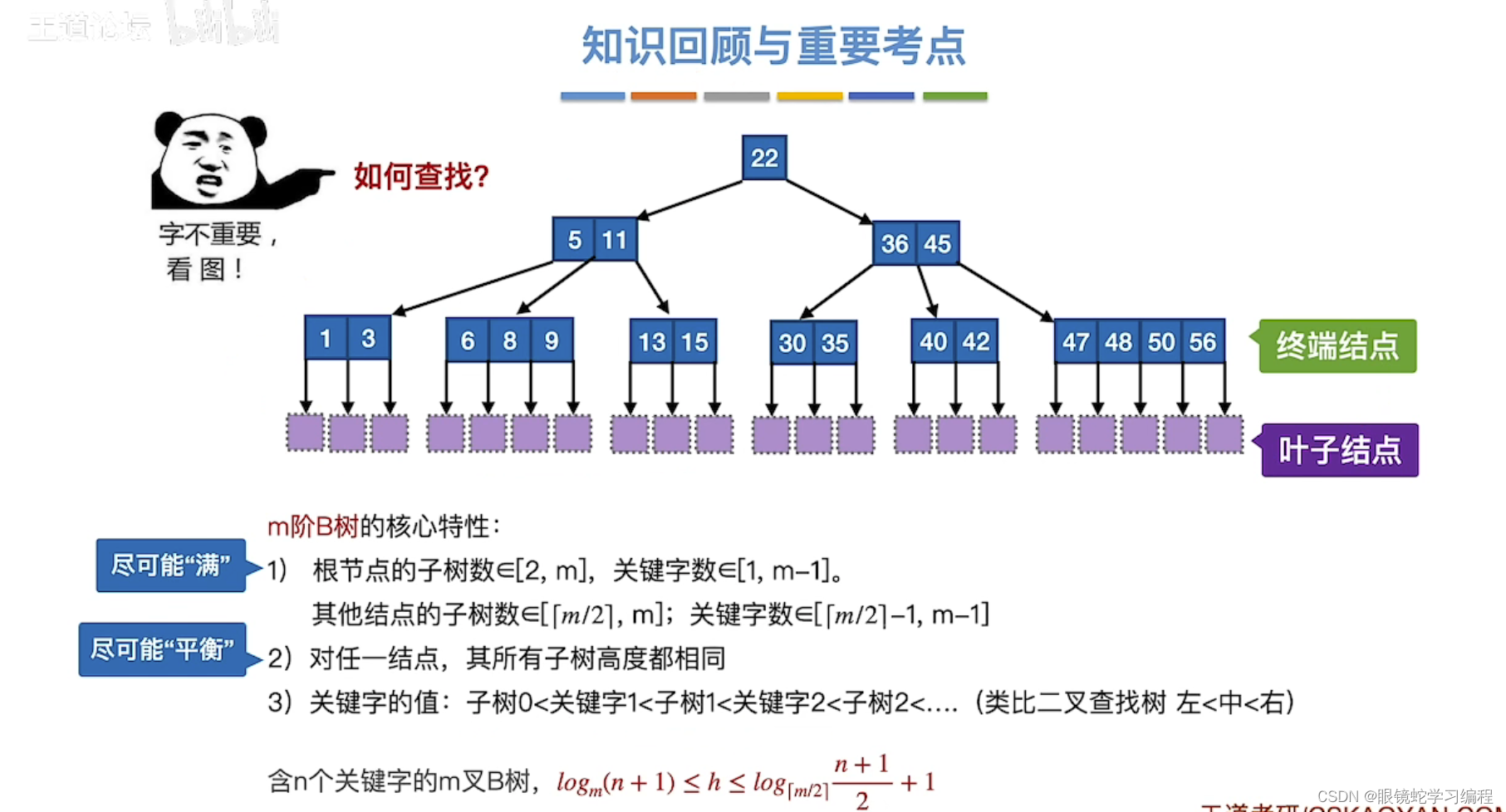
B树的插入和删除

以5阶的插入来演示过程

依次放 25，38，49，60，

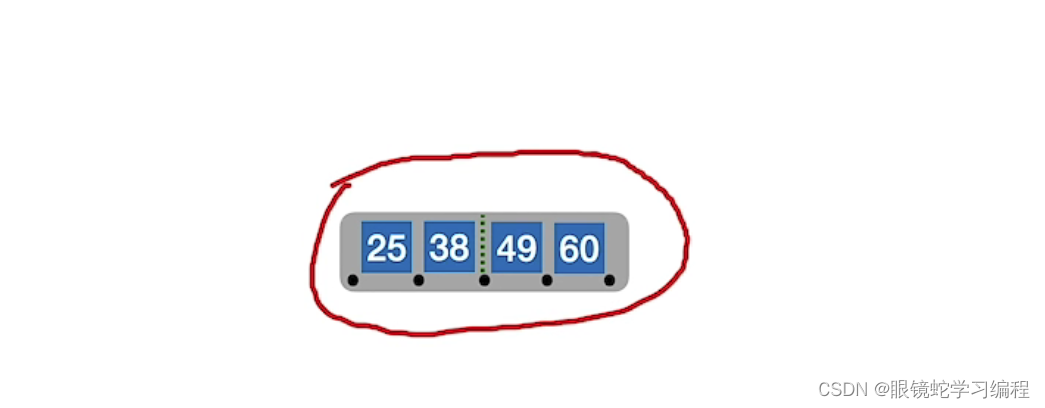
放80，导致关键字超出了4个

此时要进行分裂

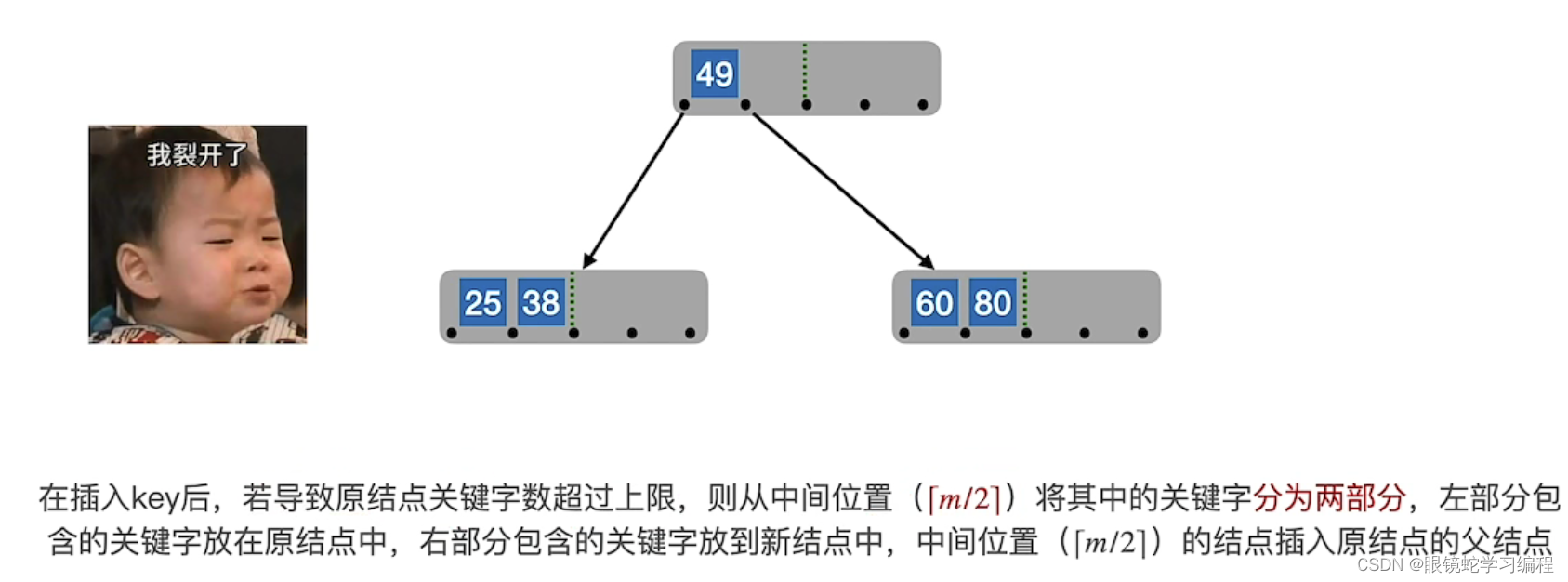
新元素一定是插入到最底层“终端结点”，用“查找”来确定插入位置

插入要保证这个结点的左边结点要比其小，右边要比关键字大

接着插入90

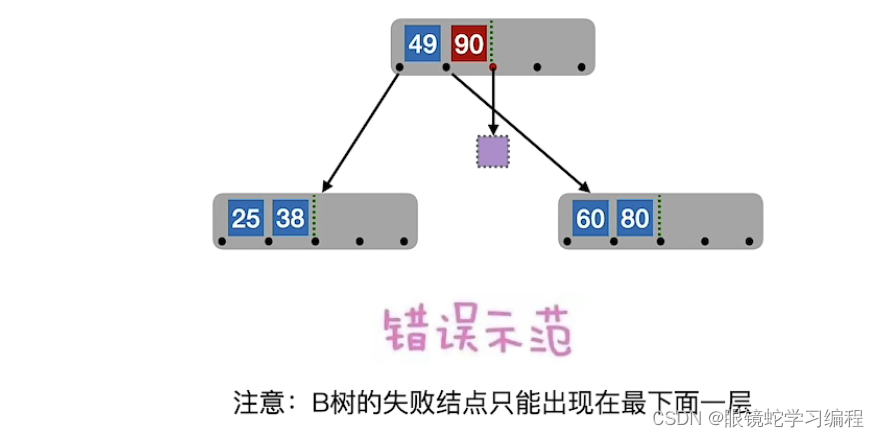
90的正确的插入位置应该如下，接着插入99

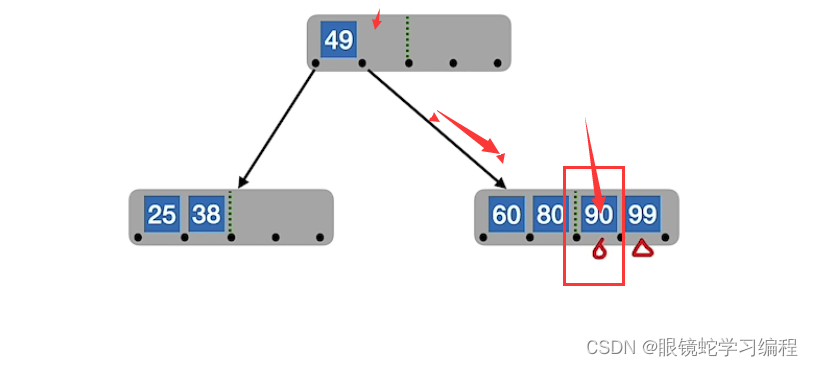
接着插入88

所以插入88的结果如下

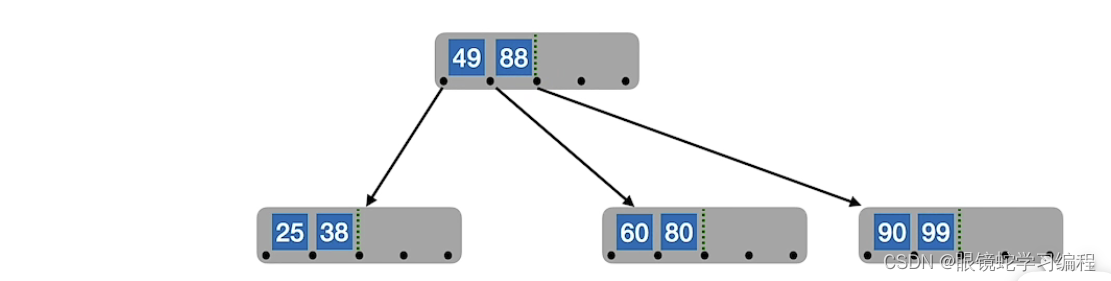
接着插入70，83，87肉眼可见往最低层插入，发现出现了溢出，将关键字[m/2]（向上取整）分成两部分即87位置

即最终插入80的位置如下

接着插入如果导致父节点也出现溢出，接着分裂，直至传到根节点为止。

 

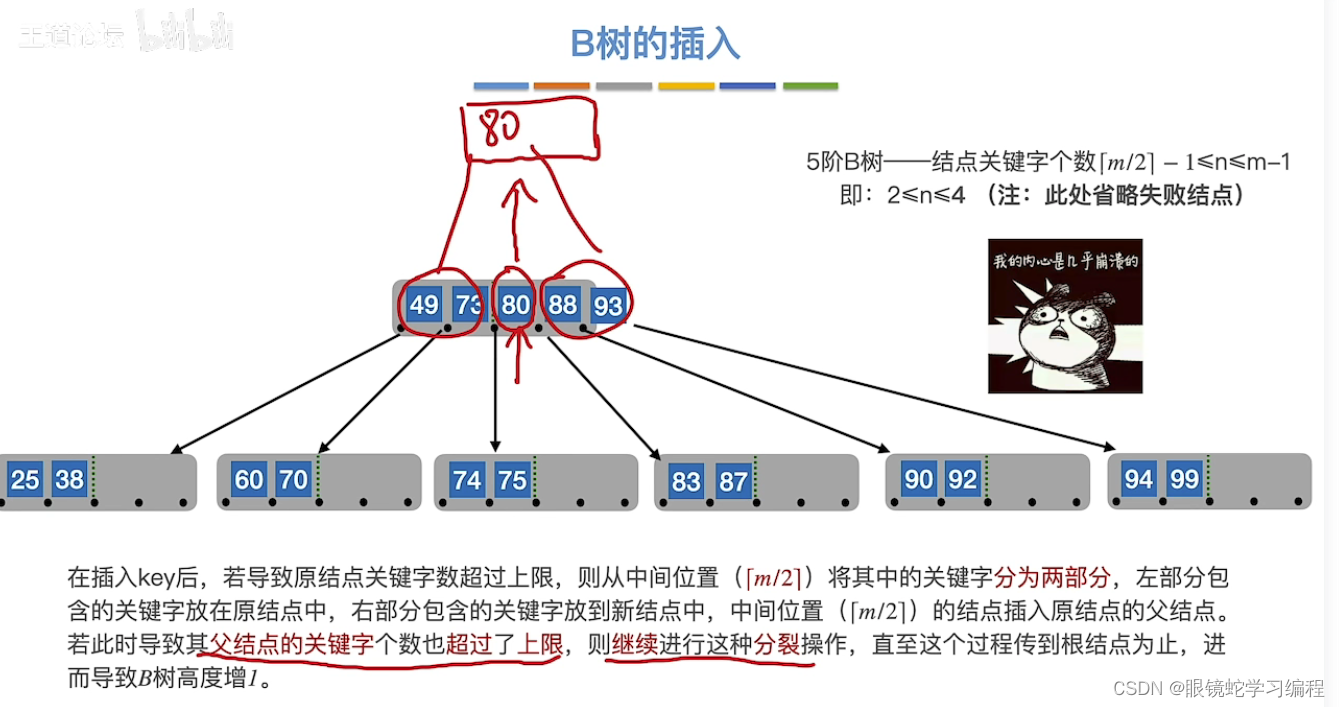
概括B树的插入方法如下

 B树的删除

（1）删除60

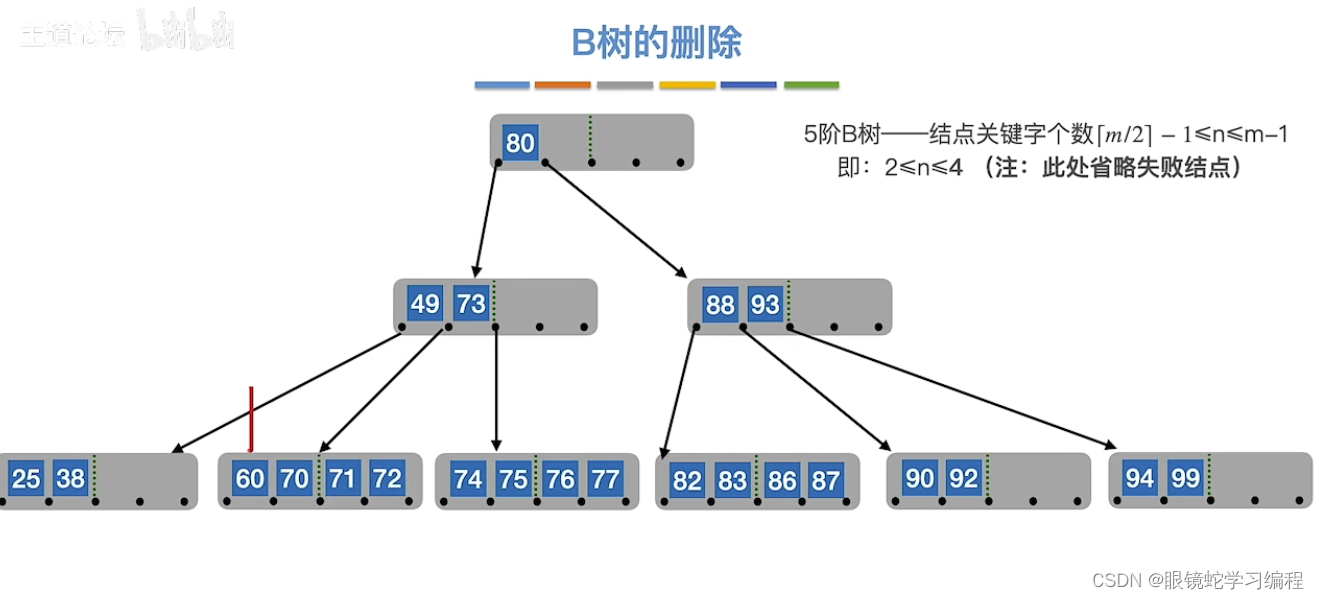
删除结果如下

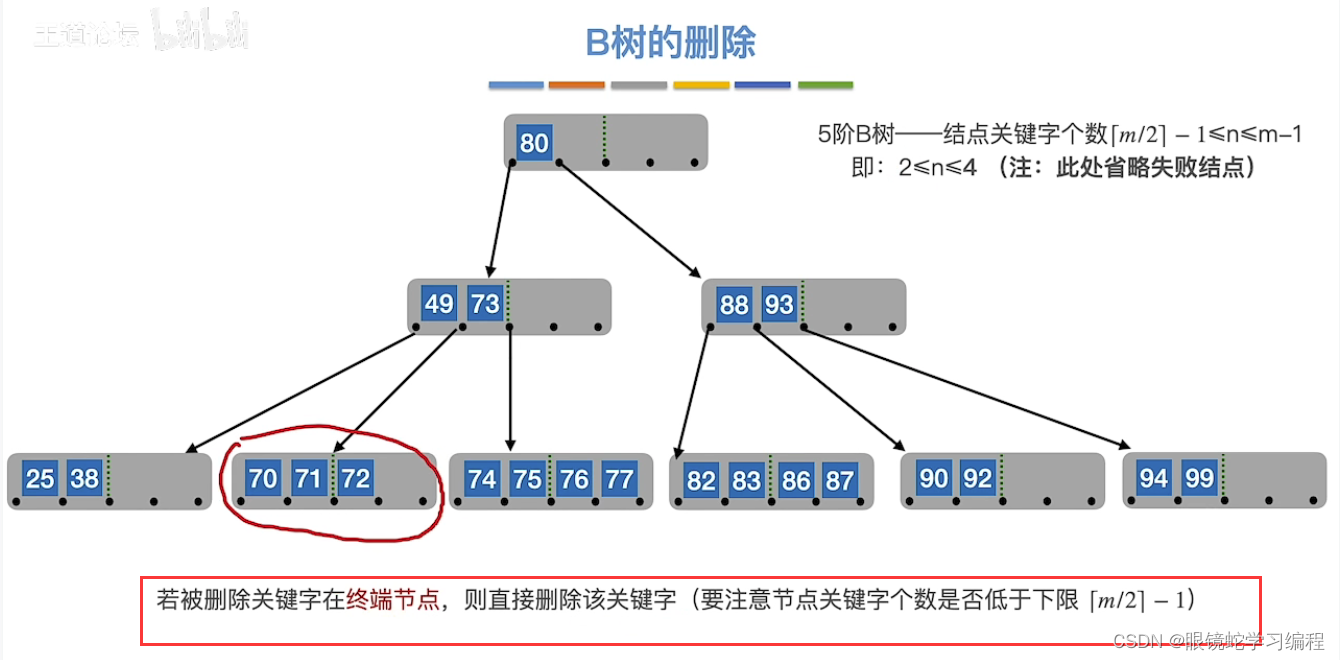
如果删除80结点，会导致根结点为空

方法找直接前驱或者直接后继

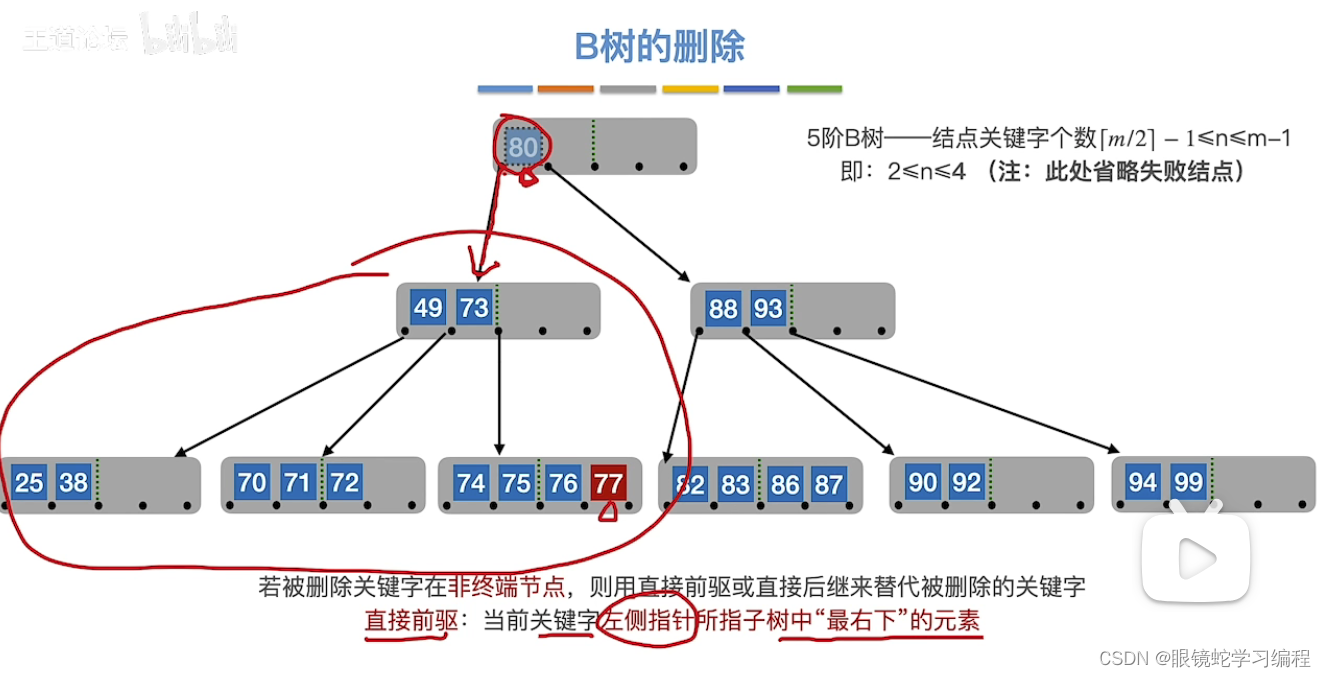
此时用直接前驱70替代了80的位置，如下图

找直接前继的发法：关键字左侧指针所指子树中“最右下”的元素

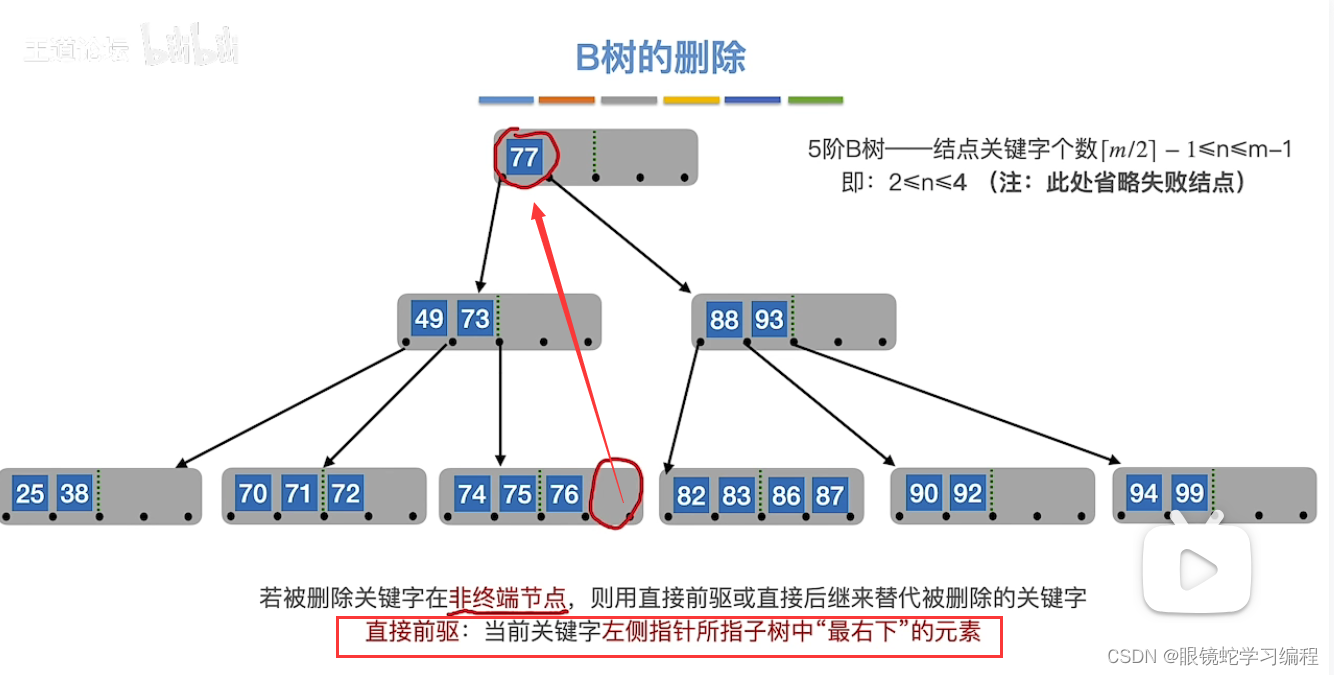
接着删除77，如果利用77的直接后继，替代删除的元素77

找直接后继的发法：关键字右侧指针所指子树中“最左下”的元素

对非终端结点关键字的删除，必然可以的转化为对终端结点的删除操作

导致删除时，结点不满足关键字的个数范围时（需要借）

比如删除38后，导致结点不满足关键字的个数范围2<=n<=4时,需要借，如果借右兄弟时

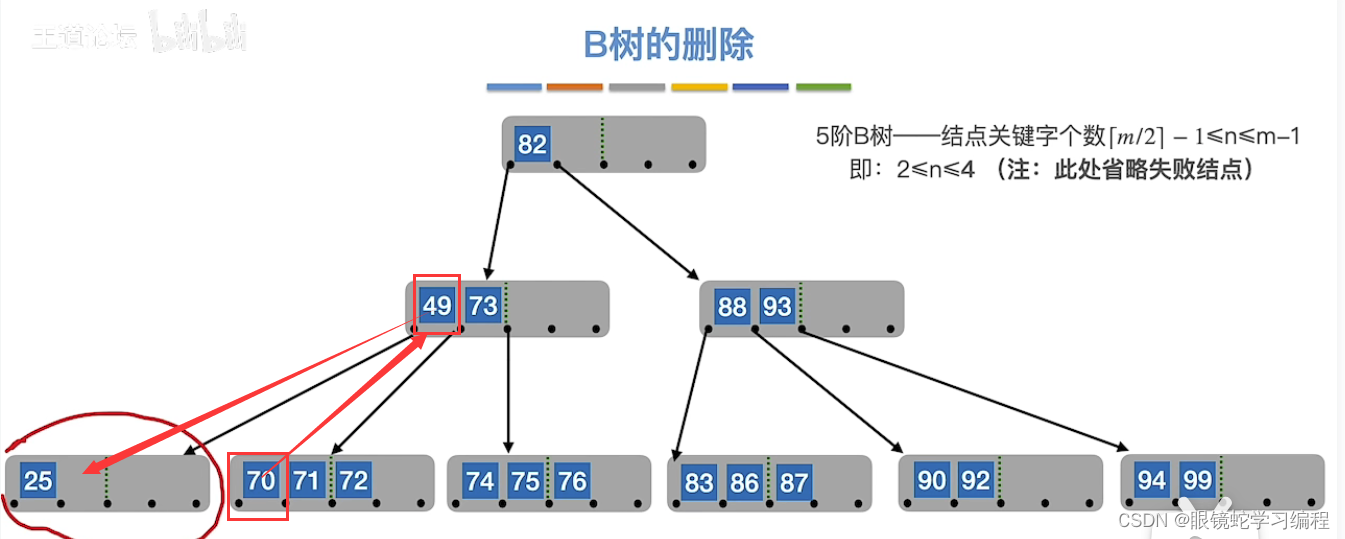
删除结果如下

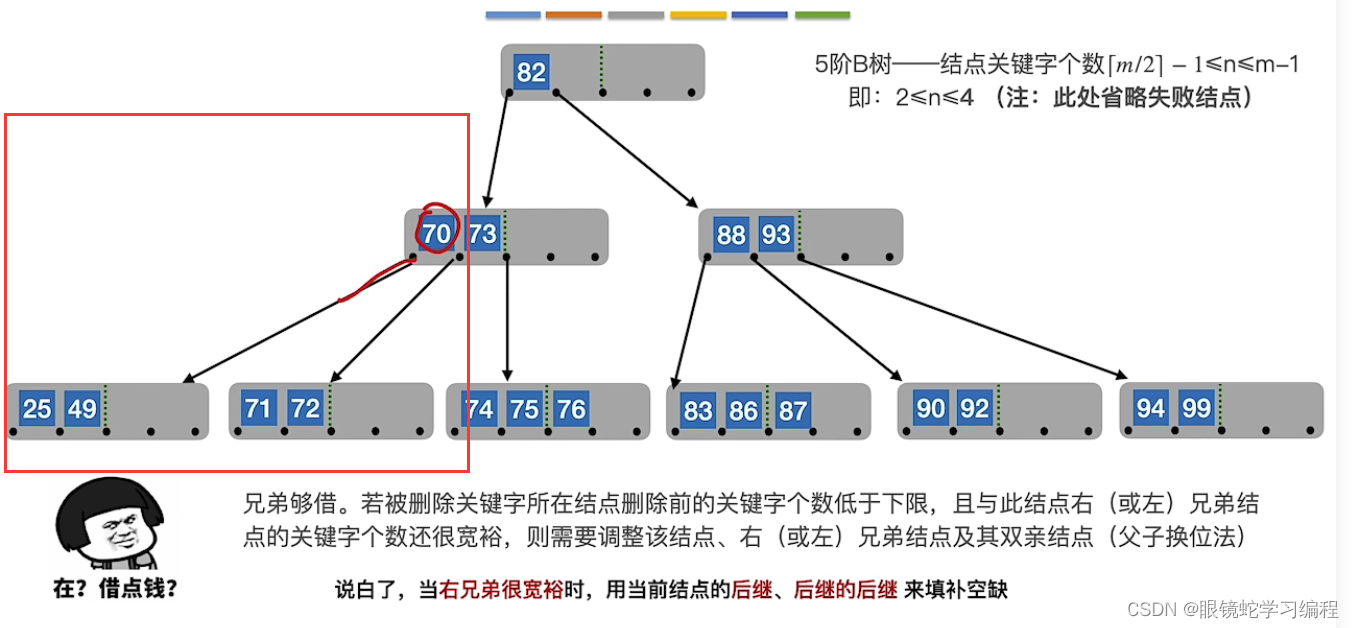
删除90后，导致关键字只剩下92，不在范围内，同时右兄弟手头紧张时，现象如下

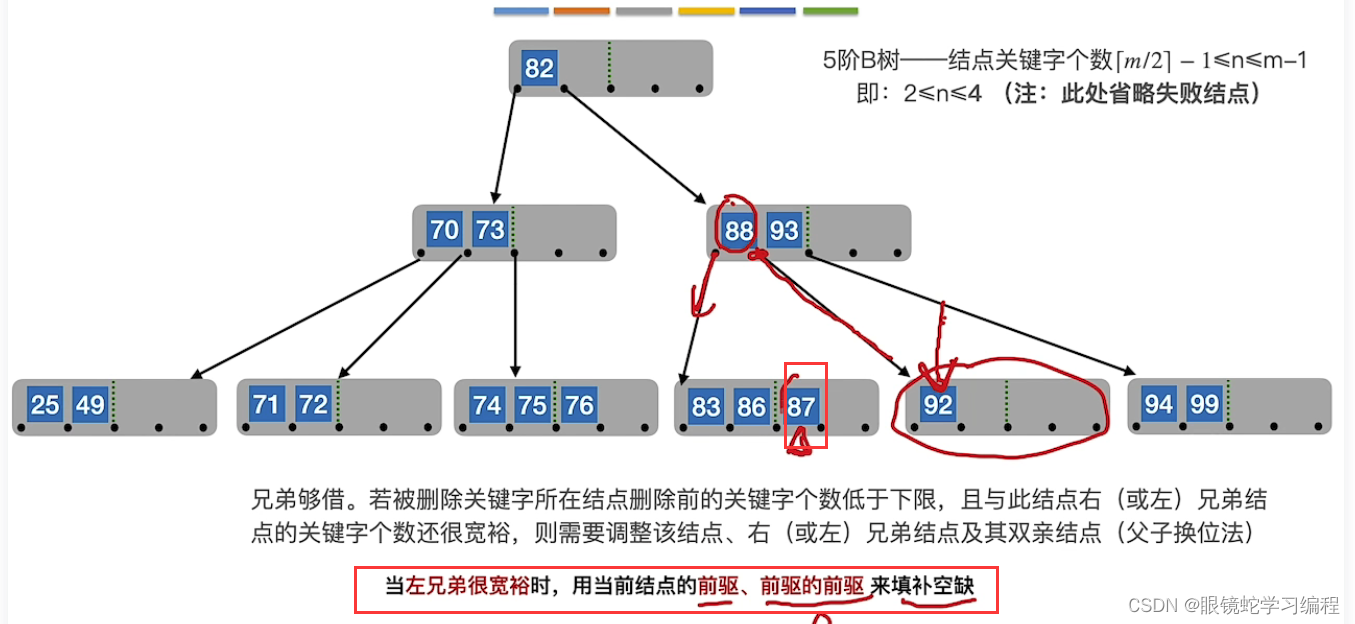
借左兄弟 

92的前驱所连指针是88，88前驱是左孩子的最右边结点87，用88插入到92前面，再用87替代88位置，

删除92后的最终结果B树是

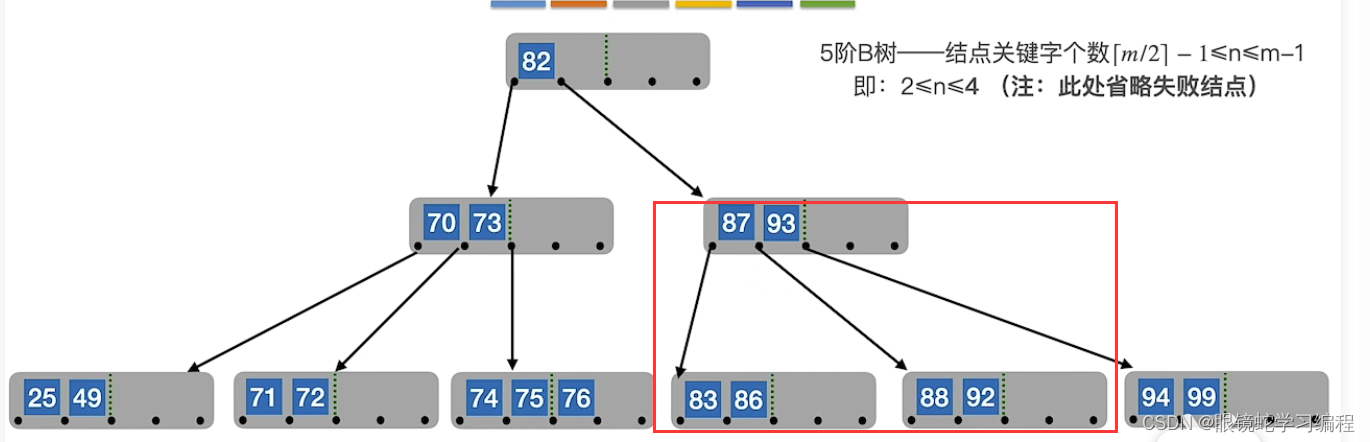
关键：

要永远保证   子树0<关键字1<子树1<关键字2<子树2<

如果兄弟不够借，需要合体

如果删除49后形成如下情况，左右兄弟不够借

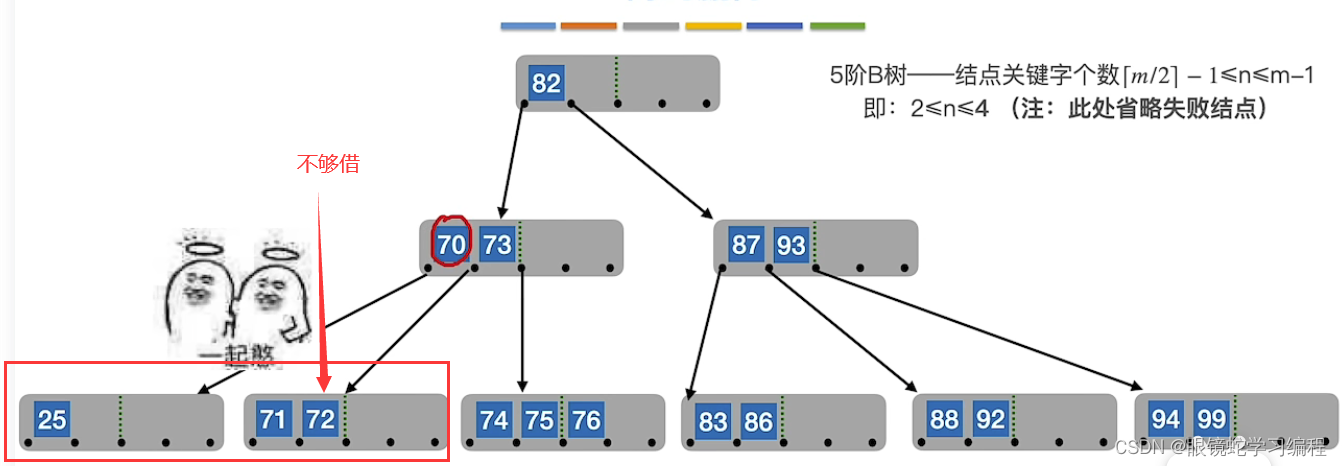开始合并，但是要永远保证   子树0<关键字1<子树1<关键字2<子树2<，从父节点要来70，但是导致父节点又不够了

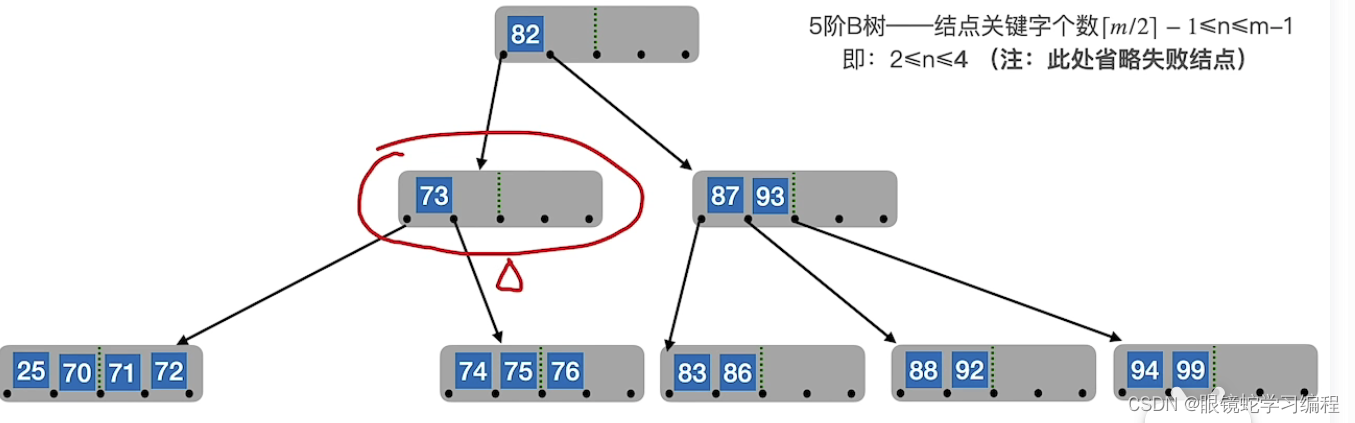接着合并

 

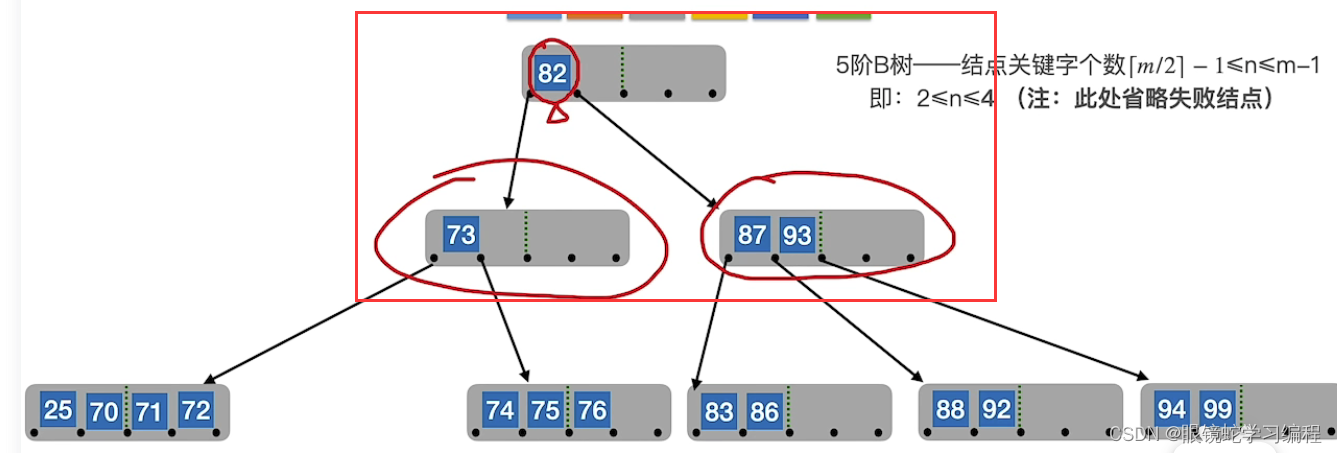
删除最终的结果如下：

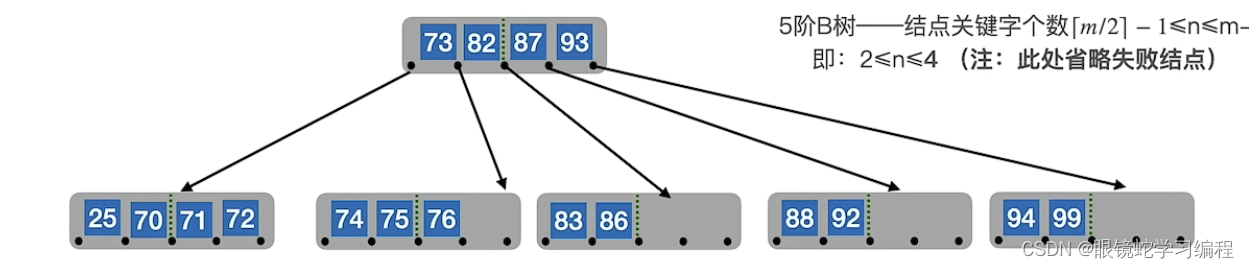
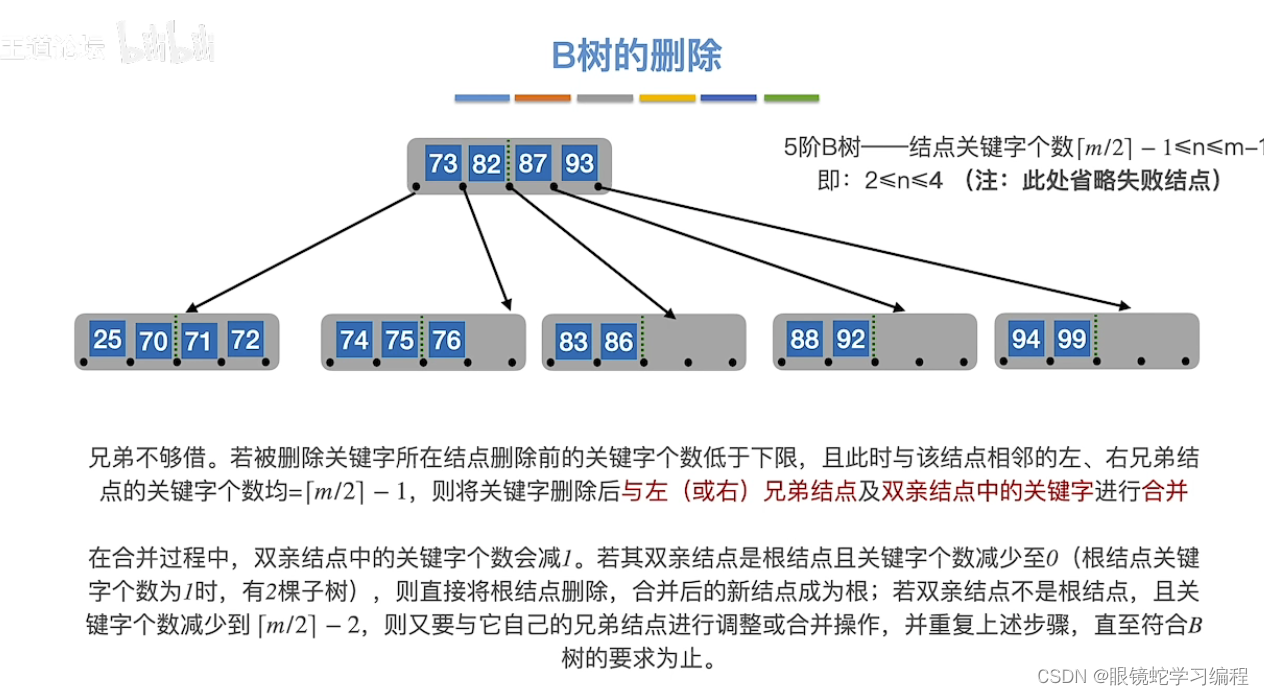
回顾B树的删除

B+树

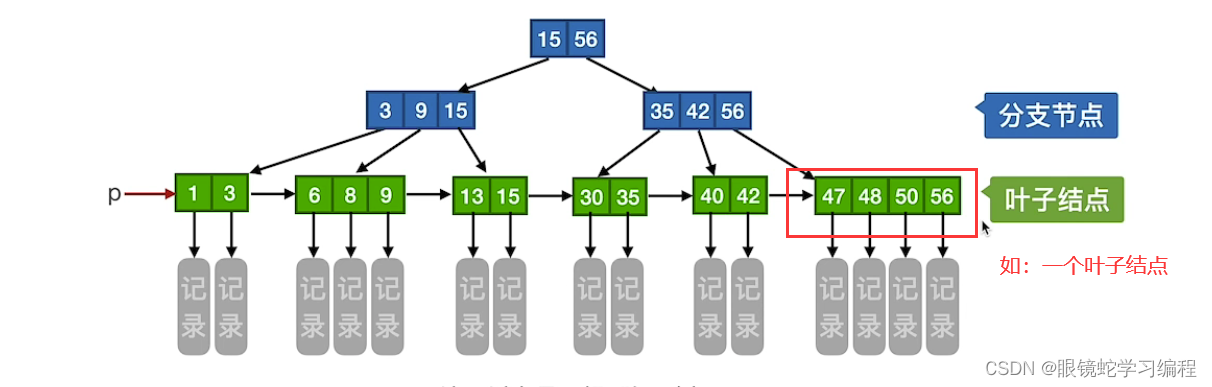
上一层的一个关键字是其子树对应的最大值，比如叶子结点中1，3，最大的的是3，所以的父节点的一个关键字是3。接着叶子结点6，8，9最大的的是9，所以的父节点的另一个关键字是9，同理，从下往上找最大的值，作为上一层的一个关键字

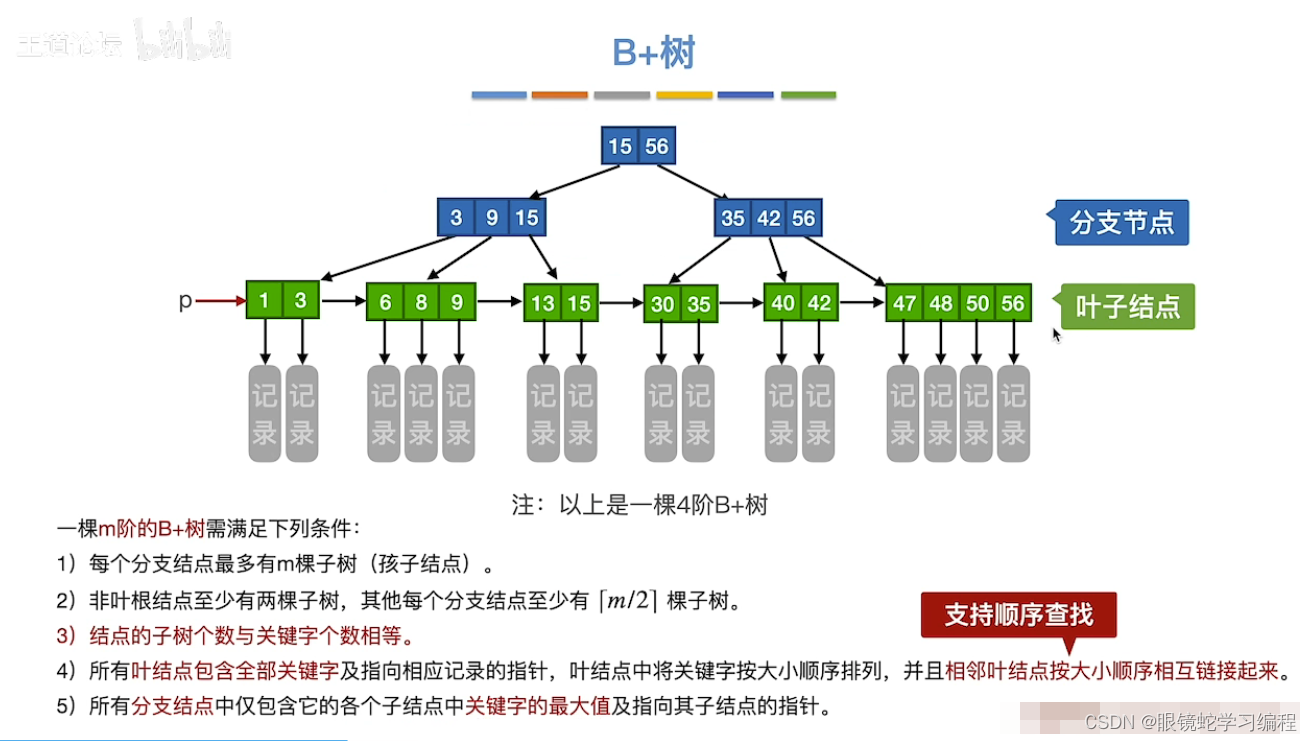
注意的点：

3）重点：B+树的结点的子树个数与关键字个数相等

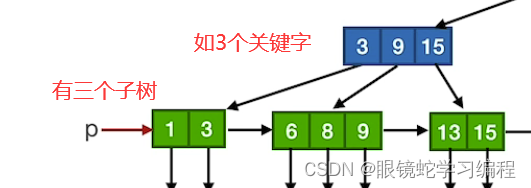
而B树如果有2个关键字是有3个子树的，如下图

4）叶子结点是整个的一块，比如47，48，50，56这个整体，并不是里面的某一部分，所以一个叶子结点可能包含m个关键字

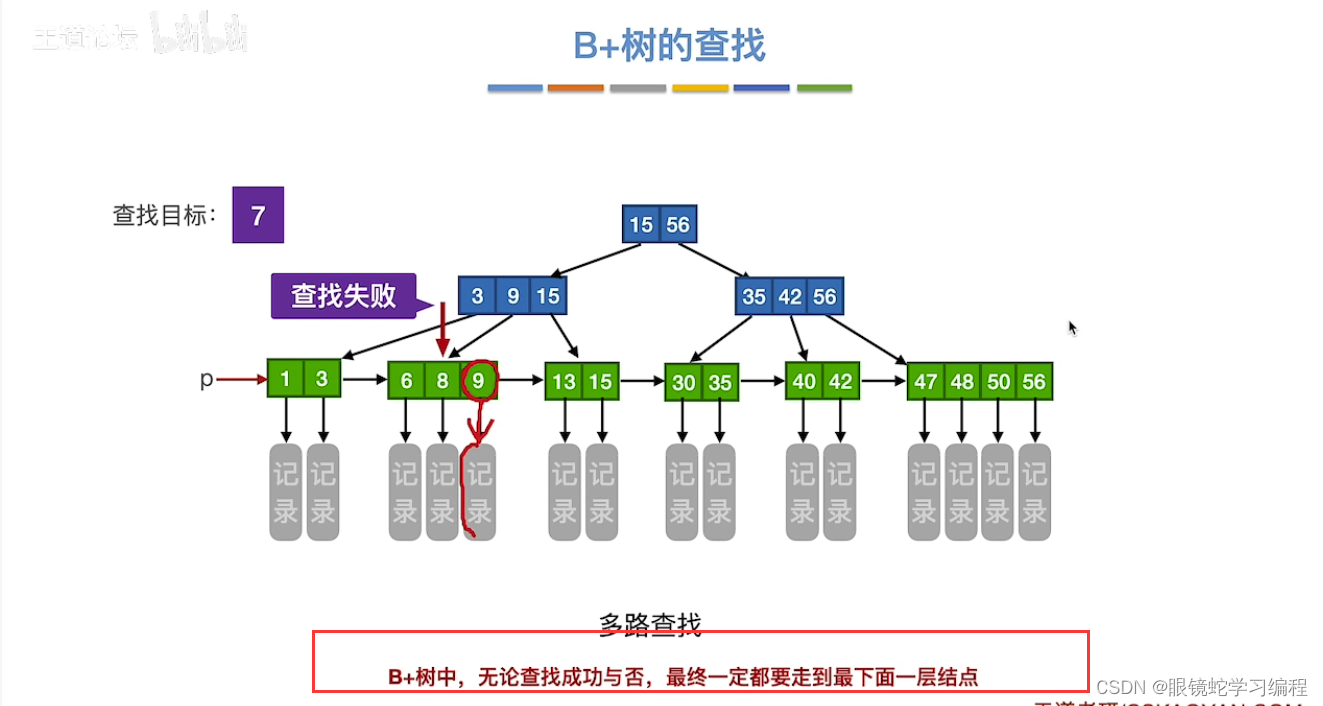
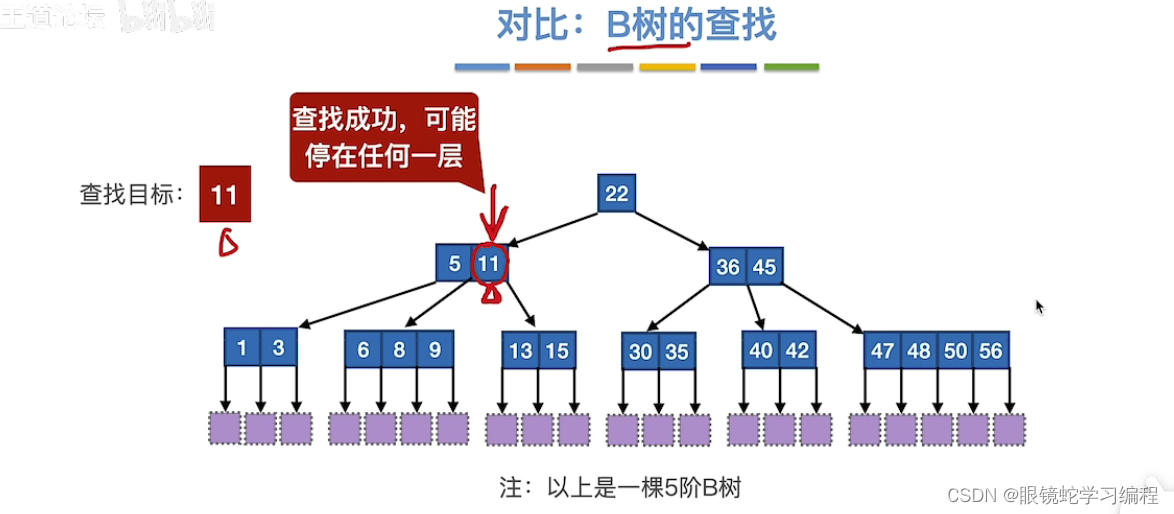
 B+树的查找

方式（1）

通过根节点往下查找，但是必须找到最下层，即叶子结点才可以，因为叶子结点才记录信息

 

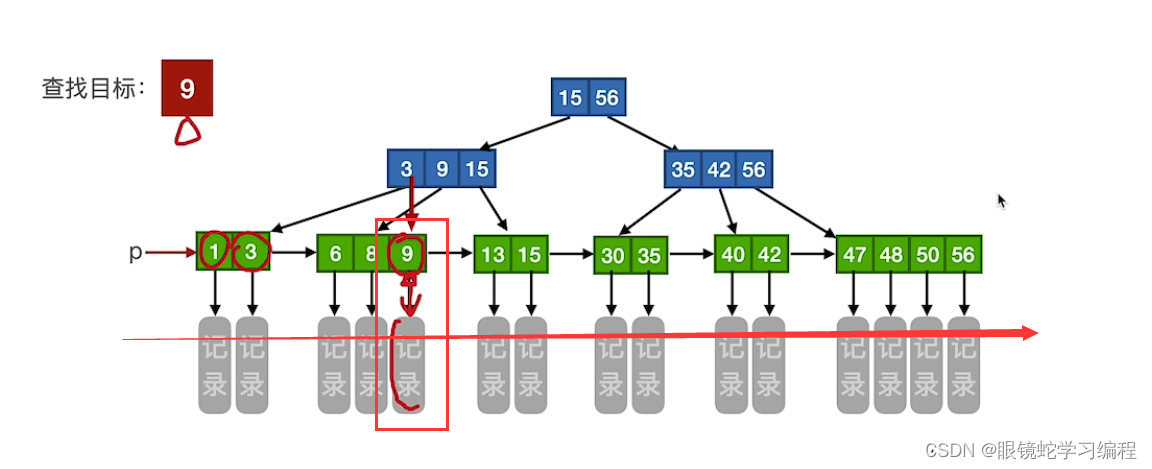
方式2

可以从保存的指针p，查找

 

回顾B+树

 

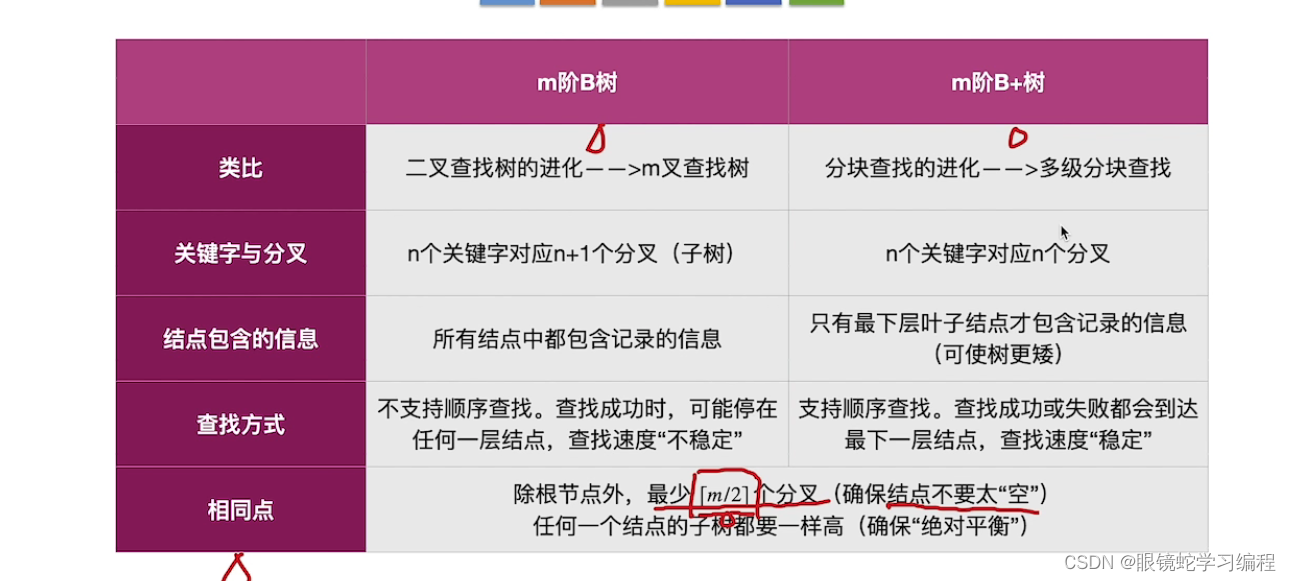
B+树与B树对比

 

 

相关文章：

数据结构--B树

目录 回顾二叉查找树 如何保证查找效率 B树的定义 提炼 B树的插入和删除 概括B树的插入方法如下 B树的删除 导致删除时&#xff0c;结点不满足关键字的个数范围时&#xff08;需要借&#xff09; 如果兄弟不够借&#xff0c;需要合体 回顾B树的删除 B树 B树的查找 …...

编程日记 2023/10/19 7:54:17

【音视频|ALSA】基于alsa-lib开发ALSA应用层程序--附带源码

&#x1f601;博客主页&#x1f601;&#xff1a;&#x1f680;https://blog.csdn.net/wkd_007&#x1f680; &#x1f911;博客内容&#x1f911;&#xff1a;&#x1f36d;嵌入式开发、Linux、C语言、C、数据结构、音视频&#x1f36d; &#x1f923;本文内容&#x1f923;&a…...

编程日记 2023/10/19 7:51:15

嵌入式养成计划-43----QT QMainWindow中常用类的使用--ui界面文件--资源文件的添加--信号与槽

一百零九、QMainWindow中常用类的使用 109.1 菜单栏 QMenuBar 菜单栏 QMenuBar 最多只能有一个 109.2 工具栏 QToolBar 工具栏 QToolBar 可以有多个 109.3 状态栏QStatusBar 状态栏 QStatusBar 最多只能有一个 109.4 浮动窗口QDockWidget 浮动窗口 可以有多个 109.5 代…...

编程日记 2023/10/19 7:50:14

【Yarn】清除Yarn的缓存，更新Yarn本身、更新项目的依赖项

要清除Yarn的缓存&#xff0c;可以运行以下命令&#xff1a; yarn cache clean这将清除Yarn的缓存目录。 要更新Yarn本身&#xff0c;可以运行以下命令&#xff1a; yarn self-update这将下载并安装最新版本的Yarn。 如果要更新项目的依赖项&#xff0c;可以运行以下命令&a…...

编程日记 2023/10/19 7:49:13

点云从入门到精通技术详解100篇-雨雾环境下多传感器融合SLAM方法（续）

目录 4 基于球面投影的激光视觉融合里程计 4.1 引言 4.2 视觉惯性里程计 4.2.1特征点提取与匹配...

编程日记 2023/10/19 7:48:12

解决GET请求入参@NotNull验证不生效问题

一、问题 get请求NotNull验证不生效 二、解决方案 两个步骤&#xff1a; 在该方法的controller类上加Validated&#xff1b;在参数面前加NotNull&#xff1b; 三、其他注解 //被注释的元素必须为null Null //被注释的元素不能为null NotNull //被注释的元素必须为true Ass…...

编程日记 2023/10/19 7:47:11

《golang设计模式》第三部分·行为型模式-01-责任链模式（Chain of Responsibility）

文章目录 1 概念1.1 角色1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1 概念 责任链&#xff08;Chain of Responsibility&#xff09;是指将客户端请求处理的不同职责对象组成请求处理链。 客户端只需要将请求交付到该链上&#xff0c;而不需要关心链上含有哪些对象。请求…...

编程日记 2023/10/19 7:46:09

环境变量【使用命令行参数引出环境变量】

前提&#xff1a;命令行参数 大家在写C/C程序的时候肯定见过下面这种情况&#xff1a; main函数里面携带的参数&#xff0c;平常写代码过程中很少用到这两个参数&#xff0c;接下来我们就研究一下 我们也不知道 指针数组argv里面到底保存的是什么&#xff0c;也不知道这个a…...

编程日记 2023/10/19 7:43:05

【Java 进阶篇】JavaScript BOM History 详解

当用户浏览网页时&#xff0c;可以使用JavaScript的BOM (Browser Object Model)中的History对象来访问浏览器的历史记录。这个对象允许您在不更改页面的情况下导航到不同的历史记录项&#xff0c;或者查看有关用户访问过的页面的信息。 在本篇博客中&#xff0c;我们将围绕Jav…...

编程日记 2023/10/19 7:42:05

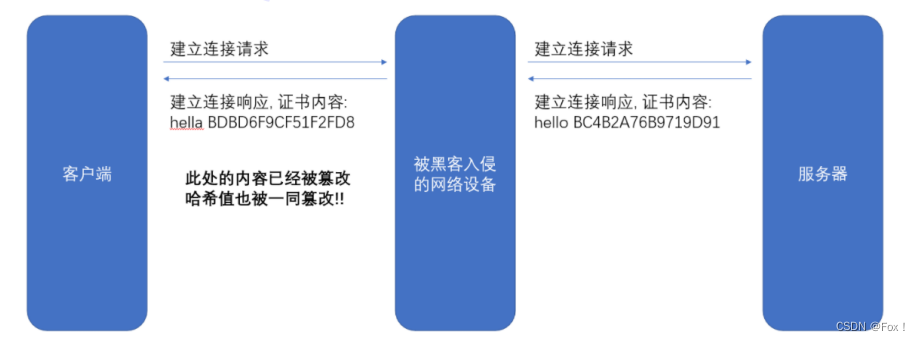
【计算机网络】https协议

文章目录 1 :peach:基本概念:peach:1.1 :apple:什么是HTTPS&#xff1f;:apple:1.2 :apple:什么是加密&#xff1f;:apple:1.3 :apple:常见的加密方式:apple:1.3.1 :lemon:对称加密:lemon:1.3.2 :lemon:⾮对称加密:lemon: 1.4 :lemon:数据指纹:lemon: 2 :peach:HTTPS的⼯作过程…...

编程日记 2023/10/19 7:40:02

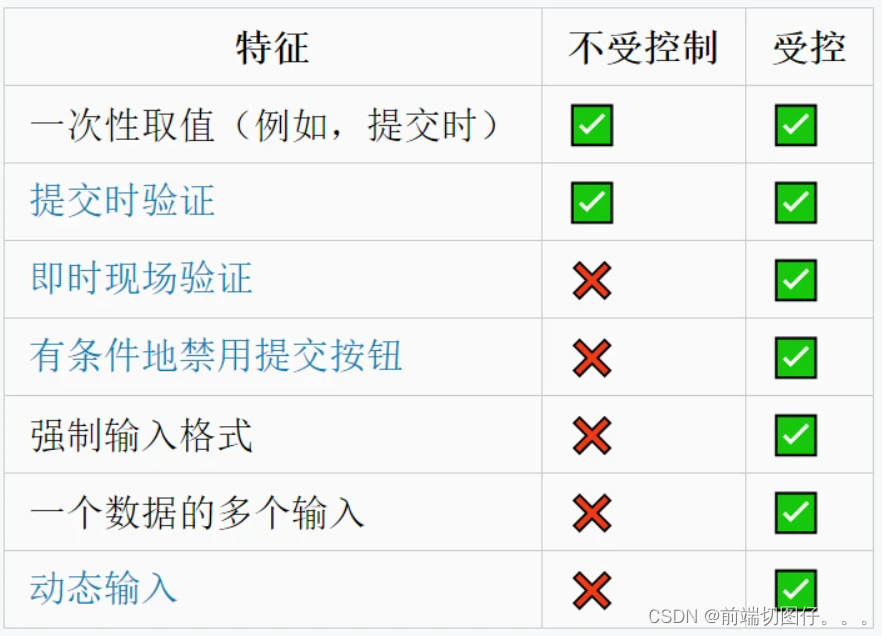
React之受控组件和非受控组件以及高阶组件

一、受控组件 受控组件&#xff0c;简单来讲&#xff0c;就是受我们控制的组件&#xff0c;组件的状态全程响应外部数据 举个简单的例子&#xff1a; class TestComponent extends React.Component {constructor (props) {super(props);this.state { username: lindaidai }…...

编程日记 2023/10/19 7:39:00

中国移动集采120万部，助推国产5G赶超iPhone15

近期媒体纷纷传出消息指中国移动将大规模集采&#xff0c;预计将采购国产5G手机120万台&#xff0c;加上另外两家运营商的集采数量&#xff0c;估计集采数量可能达到300万部&#xff0c;如此将有助于它在国内高端手机市场赶超苹果。 国产5G手机在8月底突然上市&#xff0c;获益…...

编程日记 2023/10/19 7:37:58

华为云HECS服务器下docker可视化（portainer）

一、docker安装 华为云HECS安装docker-CSDN博客 二、portainer安装 portainer地址&#xff1a;Portainer: Docker and Kubernetes Management Platform 当前portainer分CE&#xff08;开源版&#xff09; 和 BE&#xff08;商业版&#xff09;&#xff0c;用CE即可 1 创建…...

编程日记 2023/10/19 7:36:57

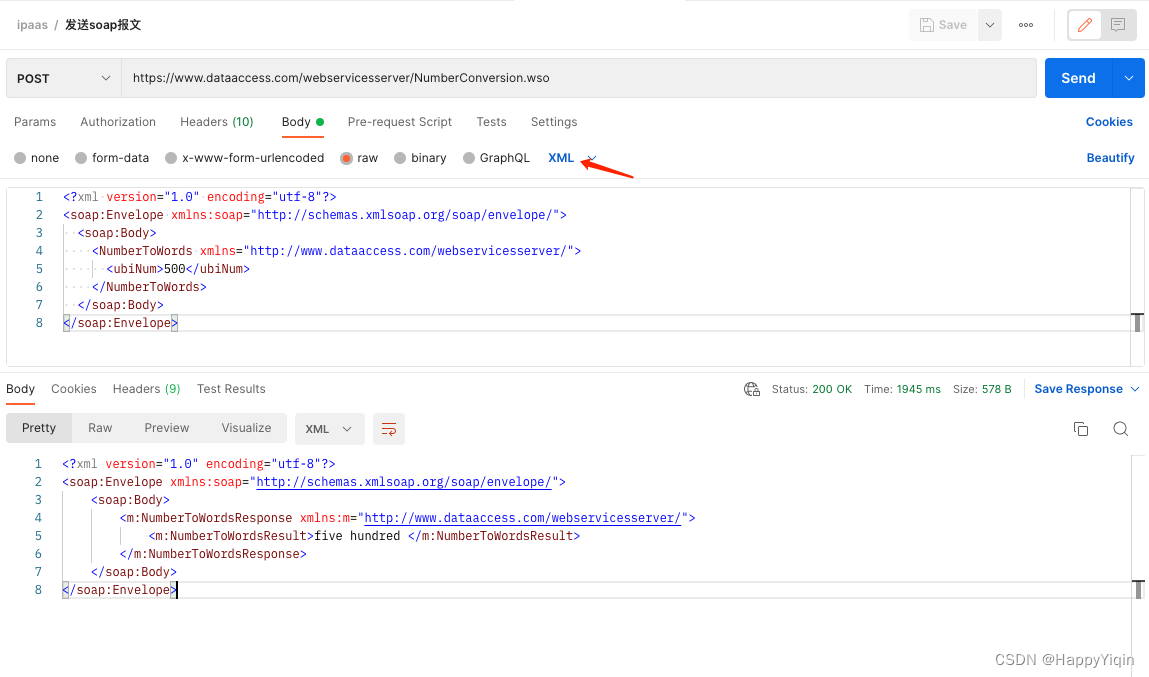
postman发送soap报文示例

一、soap简介 soap是一种基于XML的协议 二、postman发送soap请求 1、发送post请求&#xff0c;url&#xff1a;​​​ https://www.dataaccess.com/webservicesserver/NumberConversion.wso 2、headers设置&#xff0c;添加Content-Type&#xff0c;值为text/xml 添加SOAP…...

编程日记 2023/10/19 7:35:56

力扣-python-两数之和

题解&#xff1a; class Solution(object):def twoSum(self, nums, target):# 遍历列表for i in range(len(nums)):# 计算需要找到的下一个目标数字res target-nums[i]# 遍历剩下的元素&#xff0c;查找是否存在该数字if res in nums[i1:]:# 若存在&#xff0c;返回答案。这里…...

编程日记 2023/10/19 7:34:55

算水质TDS加温度补偿

先上图&#xff0c;就图里这款水质检测&#xff0c;用树莓派3/4的话&#xff0c;要配个温度检测作为温度校正&#xff0c;以及一个adc 元器件。我选ds18b20和ads1115。 再把模拟数据计算过程放一下&#xff1a; 温度检测元器件在农历钟那里提过&#xff0c;就是同款。此处先测个…...

编程日记 2023/10/19 7:33:54

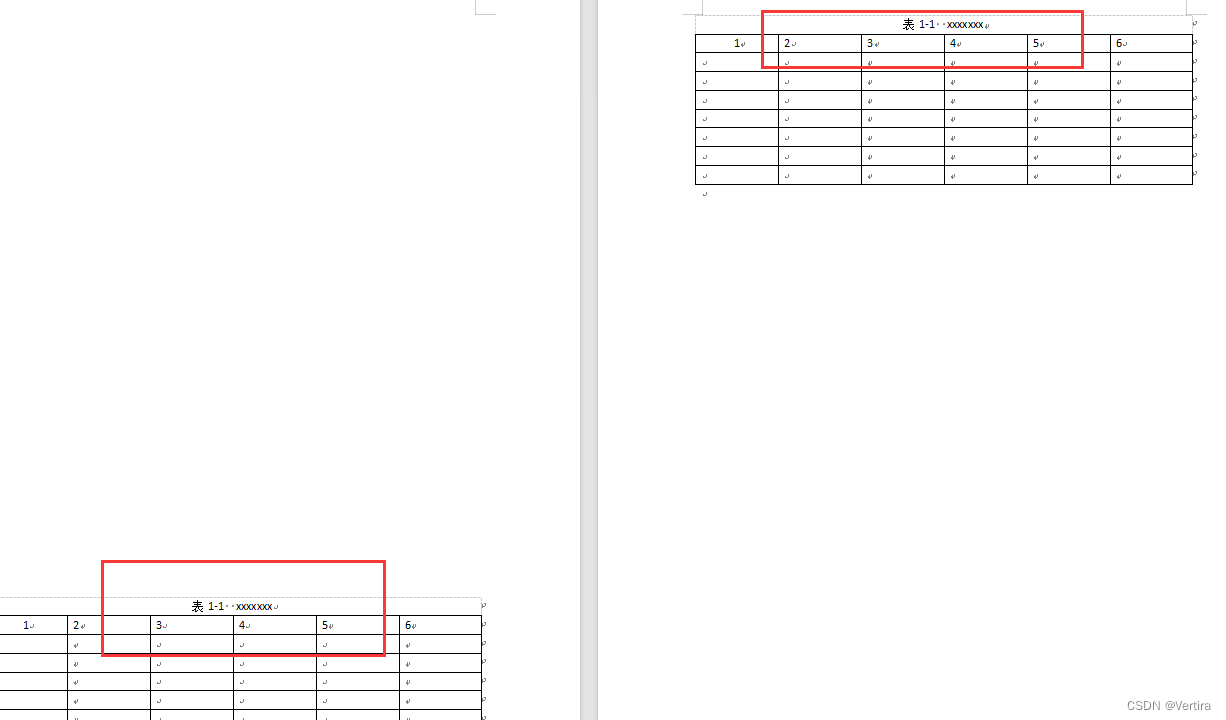
wps/word 如何让表格的标题和表格名称文本（表1-1 xxx）跨页显示（已解决）

第一步&#xff1a; 打开wps 创建一个跨页的表格表格&#xff0c;如下图 第二步 大家都知道 表格标题跨页 就是1&#xff09;在菜单表格工具 点击重复标题 或者 2&#xff09;表格属性--》行--》在各页顶端以标题行形式出现&#xff0c;详细如下图。 1&#xff09; 第一…...

编程日记 2023/10/19 7:32:53

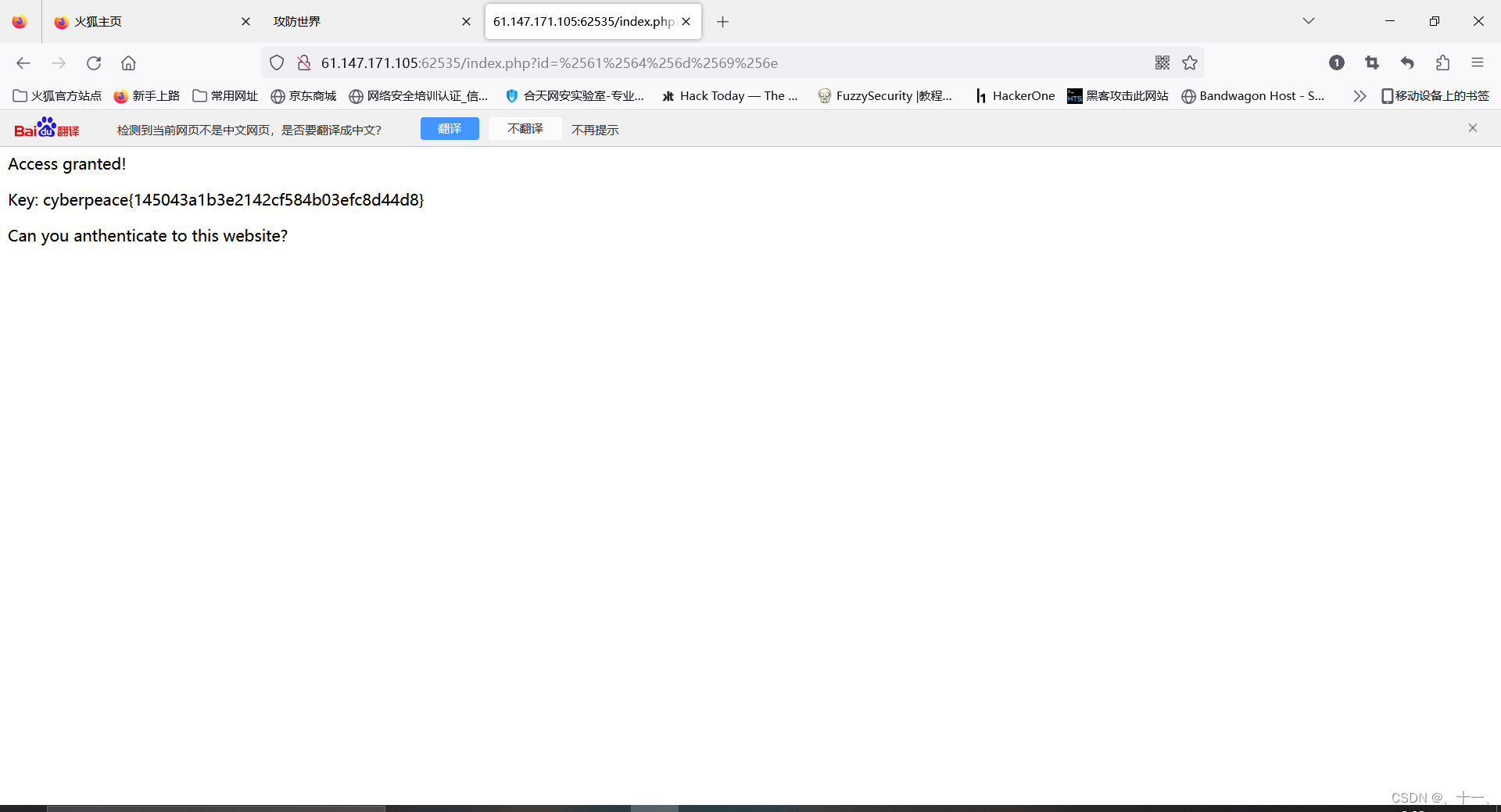
攻防世界web篇-PHP2

直接点击进入到http网页中&#xff0c;会得到这样一个界面 这里&#xff0c;我最开始使用了burp什么包也没有抓到&#xff0c;然后接着又用nikto进行探测&#xff0c;得到的只有两个目录&#xff0c;当时两个目录打开后&#xff0c;一个是fond界面&#xff0c;一个是这个网页的…...

编程日记 2023/10/19 7:31:52

Kotlin中的步长

步长是 Kotlin 中用于迭代区间或集合时控制迭代步进的概念。在 Kotlin 中&#xff0c;我们可以使用 step 关键字来指定迭代时的步长。 在 Kotlin 中&#xff0c;有多种方式可以定义一个区间&#xff08;Range&#xff09;。我们将通过以下示例代码来展示不同类型的区间以及如何…...

编程日记 2023/10/19 7:29:51

3. 无重复字符的最长子串

给定一个字符串 s &#xff0c;请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc"&#xff0c;所以其长度为 3。示例 2: 输入: s "bbbbb" 输出: 1 解释: 因为无…...

编程日记 2023/10/19 7:28:50

通过SPI传输BMI160数据到nrf528xx

目录 主控和外设之间的联系关键示例可能的bug 主控和外设之间的联系 在完成代码之前&#xff0c;我们手里会有两份代码&#xff0c;一份是nrf528xx的SDK&#xff0c;一份是BMI160传感器的SDK&#xff0c;怎么利用SDK完成我们的需求呢&#xff1f;首先我们要搞明白&#xff0c;…...

编程日记 2023/10/19 7:27:49

MAYA教程之建模基础命令介绍

基础命令 视图相关操作 旋转视图 : ALT 鼠标左键平移视图 : ALT 鼠标中键缩放视图 : 滚动鼠标滚轮 或者 ALT 鼠标右键切换视图 : 空格键回到模型 : F 视图状态 选择状态 : Q移动状态 : W旋转状态 : E缩放状态 : R 视图显示 正常显示 : 1正常圆滑同时显示 : 2圆滑显示 …...

编程日记 2023/10/19 7:26:49

文档外发控制与安全：实现高效协作与数据安全的关键

随着企业数据量的不断增加&#xff0c;文档外发成为了一个不可避免的需求。然而&#xff0c;很多企业在文档外发过程中存在着很多问题&#xff0c;如数据泄露、信息误用等。因此&#xff0c;如何保证文档外发的安全性和高效性成为了企业亟待解决的问题。飞驰云联Ftrans的文件收…...

编程日记 2023/10/19 7:25:47

在线课堂知识系统源码系统+前端+后端完整搭建教程

大家好啊&#xff0c;今天罗峰来给大家分享一款在线课堂知识系统源码系统。这款系统的功能十分强大。可以使用手机随时随地地学习&#xff0c;有专业的导师答疑解惑。支持视频&#xff0c;音频&#xff0c;图文章节。以下是部分核心代码图&#xff1a; 系统特色功能一览&#x…...

编程日记 2023/10/19 7:24:46

CSS之布局系列--顶部导航栏二级菜单居中展示

原文网址&#xff1a;CSS之布局系列--顶部导航栏二级菜单居中展示_IT利刃出鞘的博客-CSDN博客 简介 本文介绍CSS将顶部导航栏居中展示并支持二级菜单下拉展示的方法。 代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-…...

编程日记 2023/10/19 7:23:45

算法通关村第九关黄金挑战——透彻理解二叉树中序遍历的应用

大家好&#xff0c;我是怒码少年小码。 上一篇讲了二分查找&#xff0c;今天我们看看它的难度扩展。 有序数组转为二叉搜索树 LeetCode 108&#xff1a;给你一个整数数组 nums &#xff0c;其中元素已经按 升序 排列&#xff0c;请你将其转换为一棵 高度平衡 二叉搜索树。 高…...

编程日记 2023/10/19 7:22:44

【算法设计与分析zxd】第7章 贪心法

贪心算法的设计技术 • 每一步的判断都是一个当前最优的抉择&#xff0c;这个抉择计算设计的好坏&#xff0c;决定了算法的成败。 • 多步判断过程&#xff0c;最终的判断序列对应于问题的最优解 • 适用于 能够 由 局部最优达到全局最优的优化问题 【比如 求最短哈密顿回路的…...

编程日记 2023/10/19 7:21:42

CCF CSP认证 历年题目自练Day35

题目一 试题编号&#xff1a; 202305-1 试题名称&#xff1a; 重复局面 时间限制&#xff1a; 1.0s 内存限制&#xff1a; 512.0MB 问题描述&#xff1a; 题目背景 国际象棋在对局时&#xff0c;同一局面连续或间断出现3次或3次以上&#xff0c;可由任意一方提出和棋。 问题…...

编程日记 2023/10/19 7:20:41

应用crash时发送广播及信息

一、环境 高通865 Android 10 二、情景 应用崩溃时&#xff0c;将奔溃信息以广播的形式发送 二、代码位置 frameworks/base/core/java/com/android/internal/os/RuntimeInit.java private static class KillApplicationHandler implements Thread.UncaughtExceptionHandle…...

编程日记 2023/10/19 7:18:40

【亲测可用】图像目标识别入门-利用笔记本电脑摄像头识别人脸标记出来采用深度学习模型实现

更高的精度和准确性&#xff0c;可以考虑使用基于深度学习的人脸检测和识别方法&#xff0c;例如基于人脸特征的人脸检测器和具有高识别率的人脸识别模型。下面是使用基于深度学习的人脸检测和识别方法的代码示例&#xff1a; 首先&#xff0c;安装必要的库和模型&#xff1a;…...

编程日记 2023/10/19 7:17:39