深度学习 | Pytorch深度学习实践
一、overview
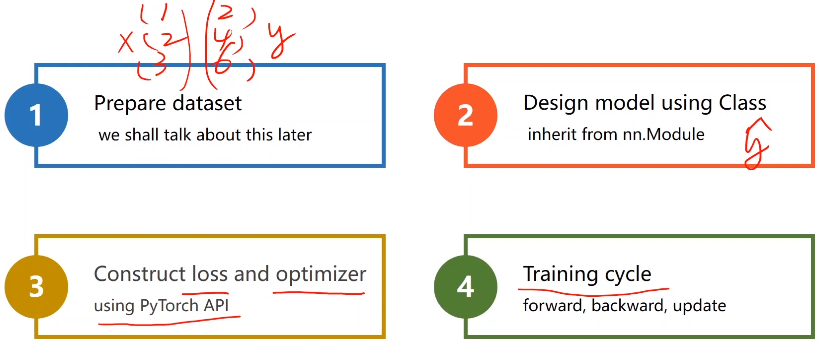
基于pytorch的深度学习的四个步骤基本如下:

二、线性模型 Linear Model
基本概念
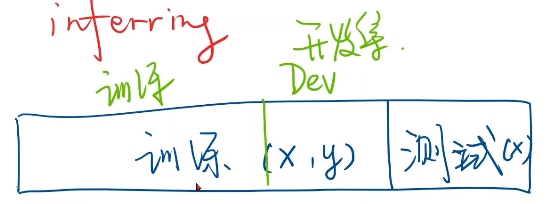
- 数据集分为测试集和训练集(训练集、开发集)
- 训练集(x,y)测试集只给(x)
- 过拟合:模型学得太多导致性能不好
- 开发集:测验模型泛化能力
- zip:从数据集中,按数据对儿取出自变量
x_val和真实值y_val

- 本例中进行人工training,穷举法
- 定义前向传播函数forward
- 定义损失函数loss
- MSE:平均平方误差

- zip:从数据集中,按数据对儿取出自变量
x_val和真实值y_val
import numpy as np
import matplotlib.pyplot as pltx_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]def forward(x):#定义模型return x * wdef loss(x,y):#定义损失函数y_pred = forward(x)return (y_pred - y) * (y_pred - y)w_list=[]#权重
mse_list=[]
for w in np.arange(0.0,4.1,0.1):print('w=',w)l_sum = 0for x_val,y_val in zip(x_data,y_data):y_pred_val = forward(x_val)loss_val = loss(x_val,y_val)l_sum += loss_valprint('\t',x_val,y_val,y_pred_val,loss_val)print('MSE=',l_sum / 3)w_list.append(w)mse_list.append(l_sum / 3)plt.plot(w_list,mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
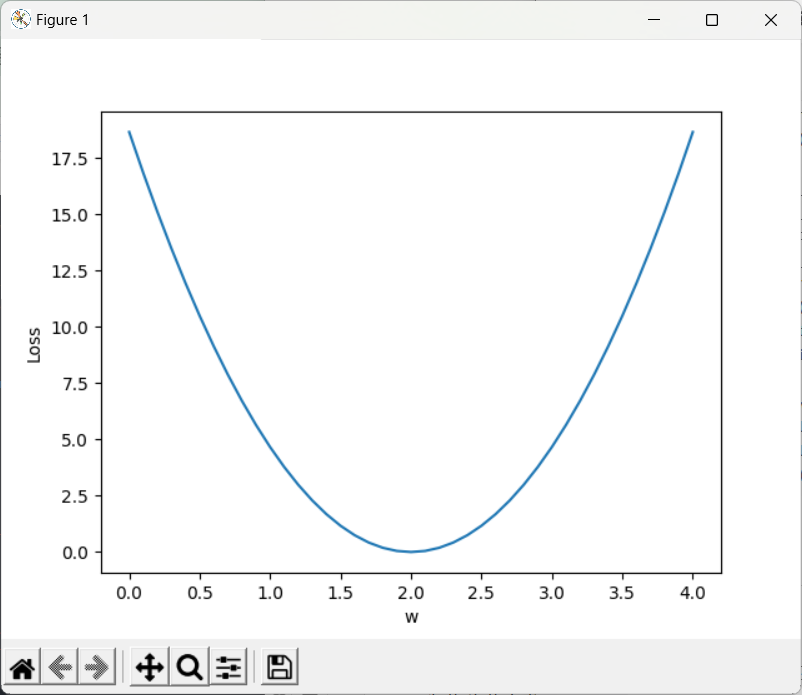
注:模型训练可视化
wisdom:可视化工具包
三、Gradient Descent 梯度下降
3.1、梯度下降
(基于cost function 即所有样本):
如我们想要找到w的最优值

- 贪心思想:每一次迭代得到局部最优,往梯度的负方向走
- 梯度下降算法很难找到全局最优,但是在深度学习中损失函数中,全局最优最有很少出现,但会出现鞍点(梯度 = 0)

import numpy as np
import matplotlib.pyplot as pltw = 1.0
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]def forward(x):return x * wdef cost(xs,ys):cost = 0for x,y in zip(xs,ys):y_pred = forward(x)cost += (y_pred-y)**2return cost / len(xs)def gradient(xs,ys):grad = 0for x,y in zip(xs,ys):grad += 2 * x * ( x * w - y)return grad / len(xs)epoch_list=[]
cost_list=[]
print('Predict (before training)',4,forward(4))
for epoch in range(100):cost_val = cost(x_data,y_data)grad_val = gradient(x_data,y_data)w -= 0.01 * grad_valprint('Epoch',epoch,'w=',w,'loss=',cost_val)epoch_list.append(epoch)cost_list.append(cost_val)
print('Predict (after training)',4,forward(4))print('Predict (after training)',4,forward(4))
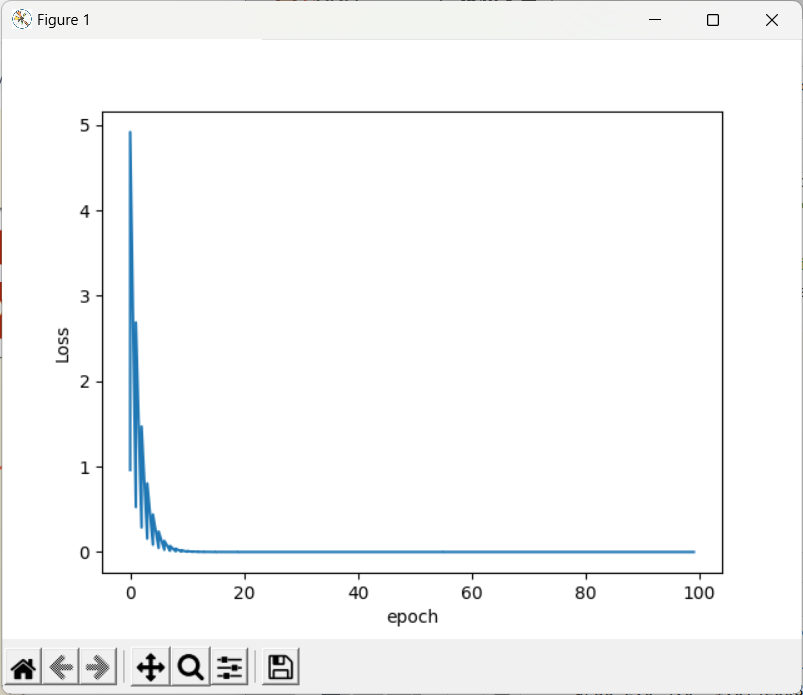
plt.plot(epoch_list,cost_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

- 注:训练过程会趋近收敛
- 若生成图像局部震荡很大,可以进行指数平滑

- 若图像发散,则训练失败,通常原因是因为学习率过大
3.2、 随机梯度下降 Stochastic Gradient Descent
(基于单个样本的损失函数):
—— 因为函数可能存在鞍点,使用一个样本就引入了随机性
此时梯度更新公式为:

与之前的区别:
- cost改为loss
- 梯度求和变为单个样本
- 训练过程中要对每一个样本求梯度进行更新
- 由于两个样本的梯度下降不能并行化,时间复杂度太高
- 所以折中的方式:使用 Mini-Batch 批量随机梯度下降
- 若干个一组,后续将会涉及
import numpy as np
import matplotlib.pyplot as pltw = 1.0
x_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]def forward(x):return x * wdef loss(x,y):y_pred = forward(x)return (y_pred-y)**2def gradient(x,y):return 2 * x * (x * w - y)loss_list=[]
epoch_list=[]
print('Predict (before training)',4,forward(4))for epoch in range(100):for x,y in zip(x_data,y_data):grad = gradient(x,y)w = w - 0.01 * gradprint('\tgrad',x,y,grad)l = loss(x,y)loss_list.append(l)epoch_list.append(epoch)print("progress",epoch,'w=',w,'loss=',l)print('Predict (after training)',4,forward(4))
plt.plot(epoch_list,loss_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show()

四 、反向传播 BackPropagation
对于复杂的网络:
举例来讲两层神经网络
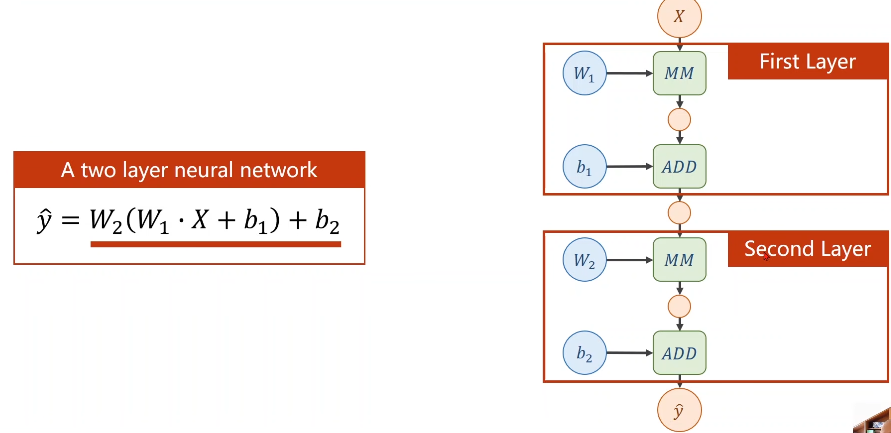
若进行线性变换,不管多少层,最终都可以统一成一种形式,但为了让你不能在化简(即提高模型复杂程度),所以我们要对每一层最终的输出
加一个非线性的变化函数(比如sigmiod)
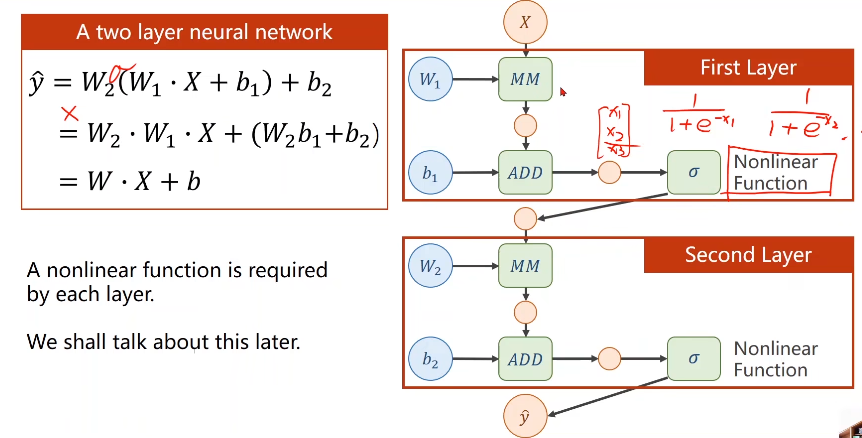
则层层叠加若需要求梯度的话就要用到 —— 链式求导:
- 1、构建计算图 —— 前馈计算(Forward)先计算最终的loss

- 2、反馈(Backward)

来看一下最简单的线性模型中的计算图的计算过程:
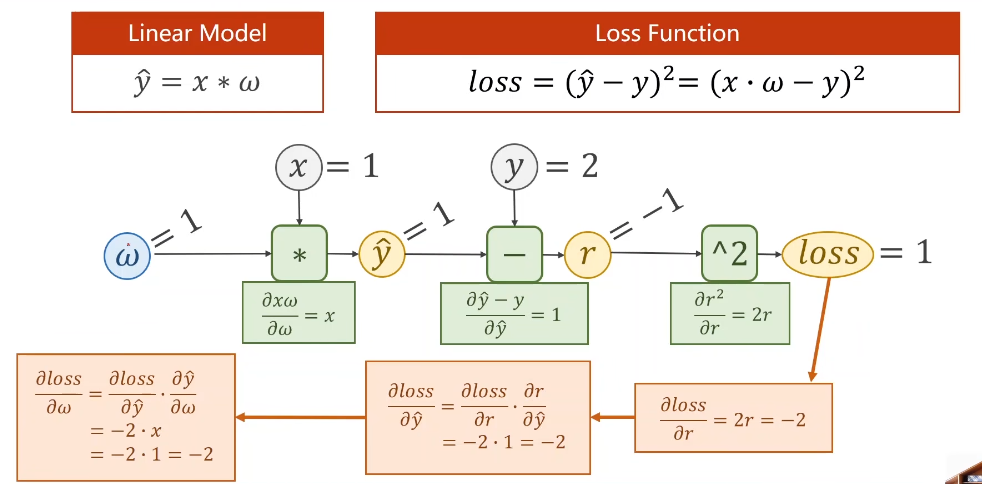

在pytorch中,使用tensor类型的数据

import torch
import matplotlib.pyplot as pltx_data = [1.0,2.0,3.0]
y_data = [2.0,4.0,6.0]w = torch.Tensor([1.0]) #注意这里一定要加[] 权重初始值
w.requires_grad = Truedef forward(x):return x * w #因为w是Tensor,这里的运算符已经被重载了,x会进行自动转换,即构造了计算图def loss(x,y):y_pred = forward(x)return (y_pred - y) ** 2epoch_list = []
loss_list = []
print('Predict (before training)',4,forward(4))for epoch in range(100):#sum=0for x,y in zip(x_data,y_data):l = loss(x,y) #只要一做backward计算图会释放,会准备下一次的图l.backward()print('\tgrad:',x,y,w.grad.item()) #item将梯度数值直接拿出来为标量w.data = w.data - 0.01 * w.grad.data #grad必须要取到data#sum += l 但l为张量,计算图,进行加法计算会构造计算图,将会发生溢出w.grad.data.zero_() #!!!权重里面梯度的数据必须显式清零print("progress",epoch,l.item())epoch_list.append(epoch)loss_list.append(l.item())print('Predict (after training)',4,forward(4))
plt.plot(epoch_list,loss_list)
plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show() 
五、利用PyTorch实现线性回归模型 Linear Regression With PyTorch
pytorch神经网络四步走
- 1、构建数据集
- 2、设计模型(用来计算y_hat)
- 3、构建损失函数和优化器(我们使用pytorch封装的API)
- 4、训练周期(前馈 反馈 更新)
本例将使用 Mini-Batch,numpy有广播机制矩阵相加会自动扩充。

使用pytorch的关键就不在于求梯度了,而是构建计算图,这里使用仿射模型,也叫线性单元。
代码实现:
import torch
import matplotlib.pyplot as plt# 1、准备数据
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])# 2、构建模型
class LinearModel(torch.nn.Module):def __init__(self): #构造函数super(LinearModel,self).__init__()self.linear = torch.nn.Linear(1,1) #构造一个对象def forward(self,x):y_pred = self.linear(x) #实现可调用对象return y_predmodel = LinearModel()# 3、构造损失函数和优化器
criterion = torch.nn.MSELoss(size_average=False) #继承nn.Module,是否求平均
optimizer = torch.optim.SGD(model.parameters(),lr=0.01) #是一个类,不继承nn.Module,不会构建计算图,lr学习率epoch_list = []
loss_list = []for epoch in range(100):# 前馈 计算 y_haty_pred = model(x_data)# 前馈 计算损失loss = criterion(y_pred,y_data)print(epoch,loss) # loss是一个对象,打印将会自动调用__str__()optimizer.zero_grad() # 所有权重梯度归零# 反馈 反向传播loss.backward()# 自动更新,权重进行更新optimizer.step()epoch_list.append(epoch)loss_list.append(loss.item())# Output weight and bias
print('w = ',model.linear.weight.item())
print('b = ',model.linear.bias.item())# Test Model
x_test = torch.Tensor([4.0])
y_test = model(x_test)
print('y_pred = ',y_test.data)
plt.plot(epoch_list,loss_list)plt.ylabel('Loss')
plt.xlabel('epoch')
plt.show() 



七、Multiple Dimension lnput
引例:糖尿病数据集分类任务
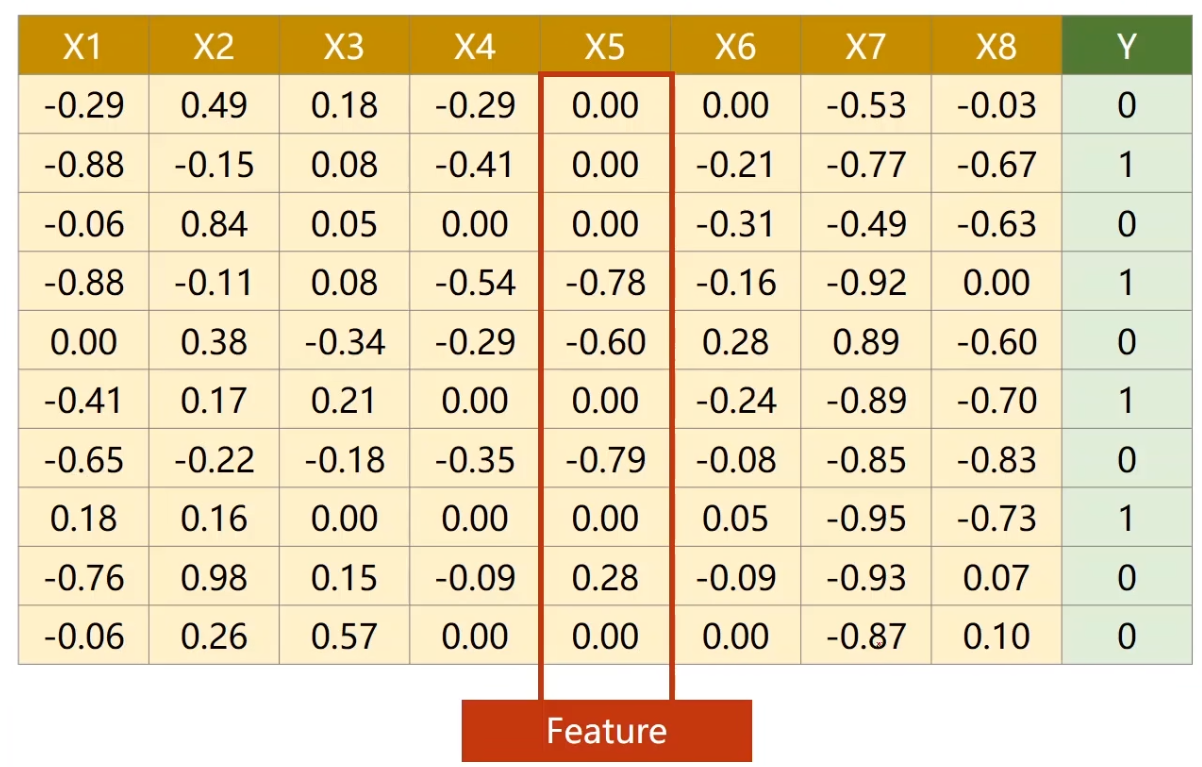
行称为:样本(Sample) 数据库中称为:记录(record)
列称为:特征 数据库中称为:字段
注:sklearn中提供一个关于糖尿病的数据集可作为回归任务的数据集

Mlultiple Dimension Loqistic Regression Model
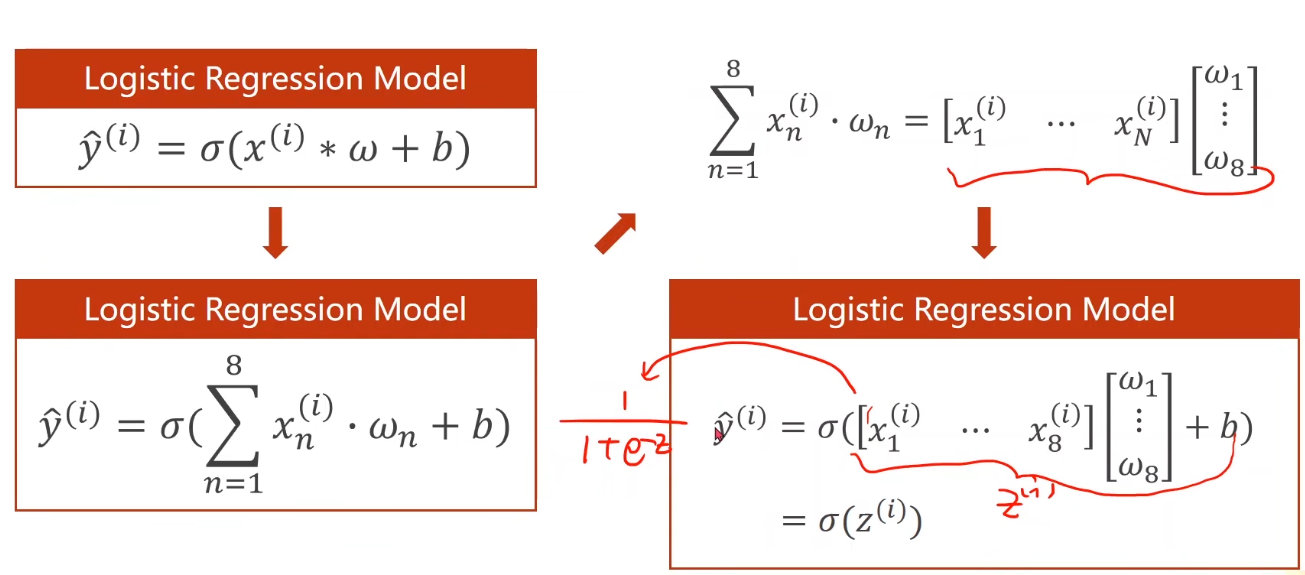
再来看下Mini-Batch(N samples)的情况

为什么这里要将方程运算转换成矩阵运算 即 向量形式呢?
———— 我们可以利用并行运算的能力,提高运行速度。

Logistics回归只有一层神经网络,若我们构造一个多层神经网络:

将矩阵看成一种空间变换的函数,这里的(8,2)是指将一个人一八维空间的向量映射到一个二维空间上,注意是线性的,而我们所做的空间变换不一定是线性的,
所以我们想要多个线性变换层通过找到最优的权重,把他们组合起来,来模拟一个非线性变换
注意绿色框中我们引入的 即激活函数 ,在神经网络中我们通过引入激活函数给线性变换加入非线性操作,这样就使得我们可以去拟合相应的非线性变换。
对于本例 Example: Artificial Neural Network

1、建立数据集
import numpy as np
import torchxy = np.loadtxt('./dataset/diabetes.csv.gz', delimiter=',', dtype=np.float32)
x_data = torch.from_numpy(xy[:, :-1])
y_data = torch.from_numpy(xy[:, [-1]])- 分隔符为,
- 为什么用float32,因为常用游戏显卡只支持32位浮点数,只有特别贵的显卡才支持64位
- 注意y,拿出来需要加中括号,拿出来矩阵
2、模型建立
class Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.linear1 = torch.nn.Linear(8, 6)self.linear2 = torch.nn.Linear(6, 4)self.linear3 = torch.nn.Linear(4, 1)self.sigmoid = torch.nn.Sigmoid()def forward(self, x):x = self.sigmoid(self.linear1(x))x = self.sigmoid(self.linear2(x))x = self.sigmoid(self.linear3(x))return xmodel = Model()
- 注意上次调用的是nn.Function下的sigmoid,但是这里调用的是nn下的一个模块
3、构造损失函数和优化器
criterion = torch.nn.BCELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)4、模型训练(这里还是全部数据)
for epoch in range(100):# forwardy_pred = model(x_data)loss = criterion(y_pred, y_data)print(epoch, loss.item())# backwordoptimizer.zero_grad()loss.backward()# updateoptimizer.step()
可以尝试不同的激活函数对结果的影响
torch.nn — PyTorch 2.1 documentation
Visualising Activation Functions in Neural Networks - dashee87.github.io
注意:Relu函数取值是0到1,如果最后的输入是小于0的,那么最后输出会是0,但我们可能会算In0,所以一般来说会将最后一层的激活函数改成sigmoid。

九、多分类问题
交叉熵损失和NLL损失到底有什么区别?
lmplementation of classifier to MNIST dataset
- ToTenser:神经网络想要的输入比较小,所以需要转变成一个图像张量

- 黑白图像:单通道
- 彩色图像:通道channel
- Normalize:标准化 切换到 0,1 分布 ,参数为 均值 标准差
- 四阶张量变成二阶张量
- 注意 最后一层不做激活

十、CNN 卷积神经网络 基础篇
首先引入 ——
- 二维卷积:卷积层保留原空间信息
- 关键:判断输入输出的维度大小
- 特征提取:卷积层、下采样
- 分类器:全连接

引例:RGB图像(栅格图像)
- 首先,老师介绍了CCD相机模型,这是一种通过光敏电阻,利用光强对电阻的阻值影响,对应地影响色彩亮度实现不同亮度等级像素采集的原件。三色图像是采用不同敏感度的光敏电阻实现的。
- 还介绍了矢量图像(也就是PPT里通过圆心、边、填充信息描述而来的图像,而非采集的图像)
- 红绿蓝 Channel
- 拿出一个图像块做卷积,通道高度宽度都可能会改变,将整个图像遍历,每个块分别做卷积
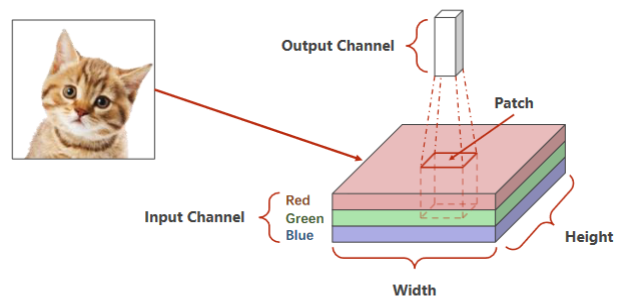
引例:
深度学习 | CNN卷积核与通道-CSDN博客
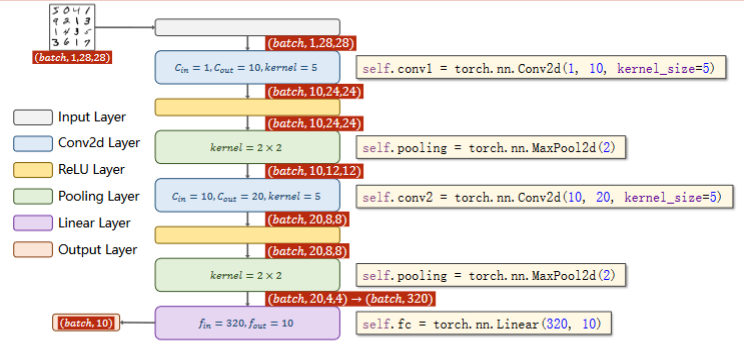
实现:A Simple Convolutional Neural Network
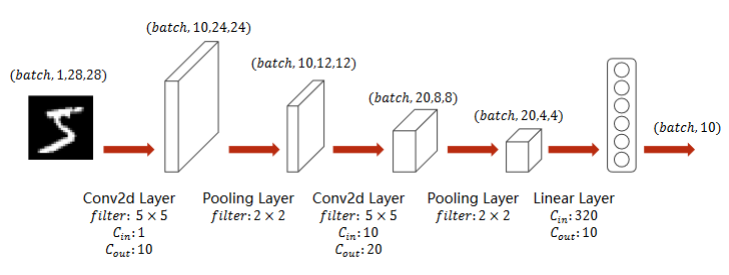
- 池化层一个就行,因为他没有权重,但是有权重的,必须每一层做一个实例
- 交叉熵损失 最后一层不做激活!
相关文章:

深度学习 | Pytorch深度学习实践
一、overview 基于pytorch的深度学习的四个步骤基本如下: 二、线性模型 Linear Model 基本概念 数据集分为测试集和训练集(训练集、开发集)训练集(x,y)测试集只给(x)过拟合…...
Elasticsearch7.9.3保姆级安装教程
Linux版本Elasticsearch版本(待安装)Kibana版本(待安装)CentOS 77.9.37.9.3 一、下载地址 1、官网下载 打开地址 https://www.elastic.co/cn/downloads/past-releases#elasticsearch,按如图所示选择对应版本即可 2、采用wget下载 为了不必要的麻烦,建…...

深入使用探讨 PuppeteerSharp 抓取 LinkedIn 页面的步骤
LinkedIn是全球最大的职业社交平台之一,拥有大量的用户和企业信息。用户可以在上面建立个人职业资料、与其他用户建立联系、分享职业经验和获取行业动态。由于其庞大的用户群体和丰富的数据资源,开发者们对于获取LinkedIn数据的需求日益增长。 Puppeteer…...

联合体(共用体)
1. 联合类型的定义 联合也是一种特殊的自定义类型。 这种类型定义的变量也包含一系列的成员,特征是这些成员公用同一块空间。 2.联合大小的计算 联合的大小 至少是最大成员的大小 。 当最大成员大小不是最大对齐数的整数倍的时候,就要对 齐到最大对齐数…...

从零开始:GitFlow详细教程,轻松掌握分支策略
前序 GitFlow是一种用于管理Git仓库中软件开发工作流程的模型,它提供了一种结构化的方法来处理特性开发、版本发布和维护。下面是一个详细的GitFlow教程,帮助你了解GitFlow的基本概念和使用方法。 安装GitFlow 首先,确保你已经安装了Git。…...

深度学习硬件介绍
目录 1. 深度学习电脑选型1.1 深度学习常用框架1.2 深度学习硬件选择1.3 GPU 厂商介绍科普 你真的需要这么一块阵列卡 1. 深度学习电脑选型 1.1 深度学习常用框架 常见的深度学习框架:百度的飞桨框架、Google 的TensorFlow,伯克利亚学院的Caffe&#x…...
利用向导创建MFC
目录 1、项目的创建: 2、项目的管理 : 3、分析以及生成的项目代码 : (1)、查看CFrame中的消息映射宏 (2)、自动生成事件 (3)、在CFrame中添加对应的鼠标处理函数 …...
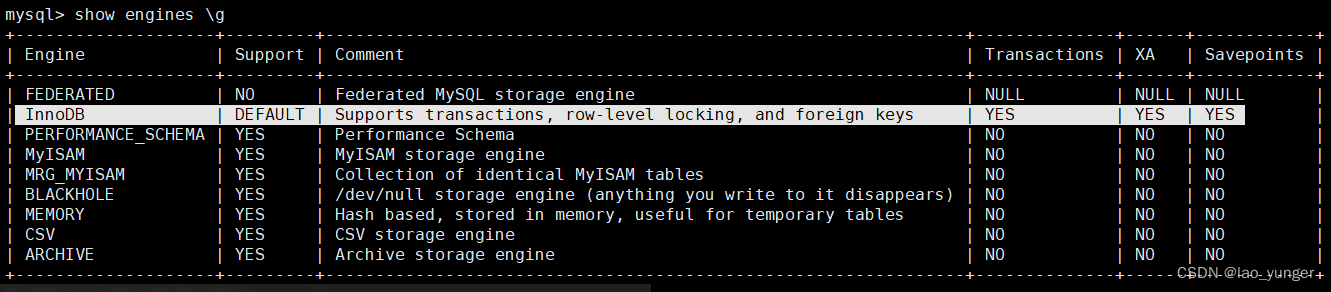
MySQL 8.0 OCP认证精讲视频、环境和题库之五 事务、缓存
redo log buffer: 缓存与事务有关的redo log ,用来对mysql进行crash恢复,不可禁用; 日志缓冲区是存储要写入磁盘上日志文件的数据的内存区域。日志缓冲区大小由innodb_Log_buffer_size变量定义。 默认大小为16MB。日志缓冲区的内容会定…...
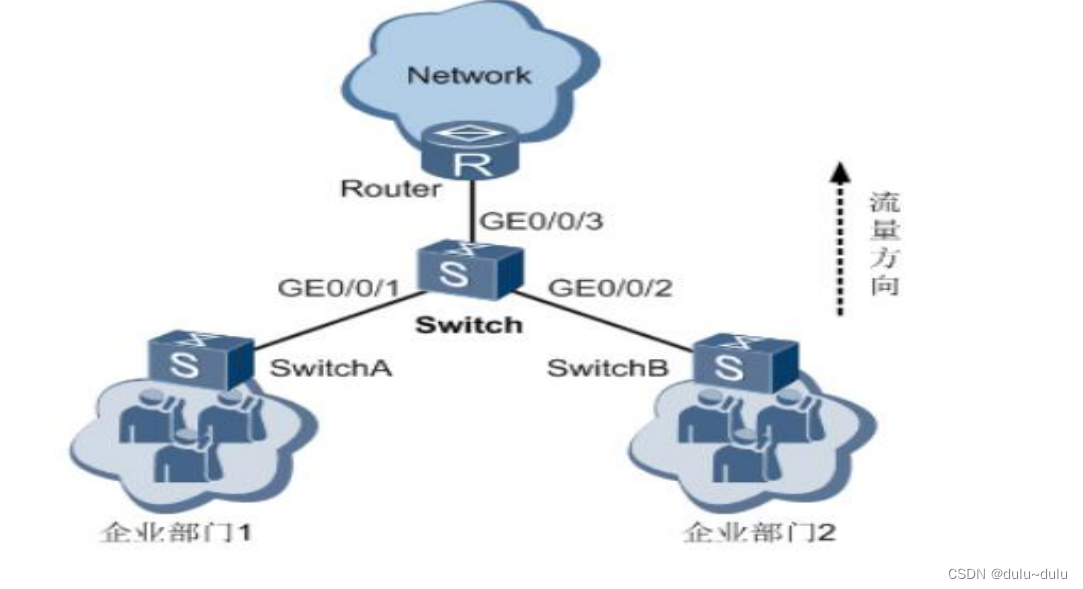
ACL配置
目录 1.使用基本ACL配置交换telnet访问的权限 2.使用高级ACL配置流分类实现限制互访某一台服务器 3.使用二层ACL配置流分类拒绝指定报文通过 4.通过流策略实现策略路由(重定向到不同的下一跳) 5.通过流策略实现不同网段间限制互访 6.通过流策略实现限速功能 7.通过流策略…...

微信小程序修改van-popup的背景颜色
效果图: van-popup背景颜色渐变 使用深度修改样式不生效,直接在 custom-style里面修改即可; <van-popup position"bottom"custom-style"height:25%;background:linear-gradient(95deg, #F8FCFF -0.03%, #EDF5FF 64.44…...
SpringCloud-Nacos
一、介绍 (1)作为服务注册中心和配置中心 (2)等价于:EurekaConfigBus (3)nacos集成了ribbon,支持负载均衡 二、安装 (1)官网 (2) …...
)
动态规划12(Leetcode221最大正方形)
代码: class Solution {public int maximalSquare(char[][] matrix) {int m matrix.length;int n matrix[0].length;int[][]area new int[m][n];area[0][0] matrix[0][0];int max 0;for(int i0;i<m;i){area[i][0] matrix[i][0]1? 1:0;max Math.max(area…...
【Git】bad signature 0x00000000 index file corrupt. fatal: index file corrupt
问题描述 电脑写代码时蓝屏。重启后 git commit 出错。 error: bad signature 0x00000000 fatal: index file corrupt原因分析 当电脑发生蓝屏或异常关机时,Git 的索引文件可能损坏。 解决方案 删除损坏的索引文件。 rm -Force .git/index回退到上一个可用的版…...

GO 语言的函数??
函数是什么? 学过编程的 xdm 对于函数自然不会陌生,那么函数是什么呢? 函数是一段可以重用的代码块,可以被多次调用,我们可以通过使用函数,提高咱们代码代码的模块化,提高程序的可读性和可维护…...
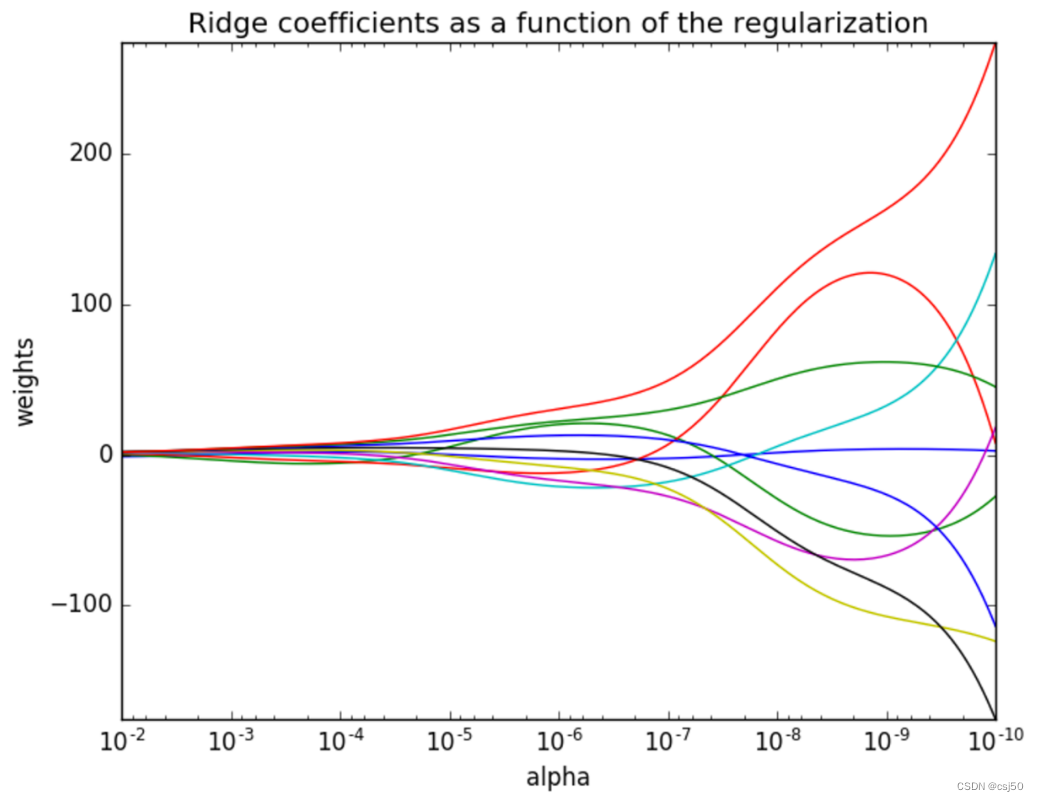
机器学习基础之《回归与聚类算法(3)—线性回归优化:岭回归》
一、什么是岭回归 其实岭回归就是带L2正则化的线性回归 岭回归,其实也是一种线性回归。只不过在算法建立回归方程时候,加上L2正则化的限制,从而达到解决过拟合的效果 二、API 1、sklearn.linear_model.Ridge(alpha1.0, fit_interceptTrue…...
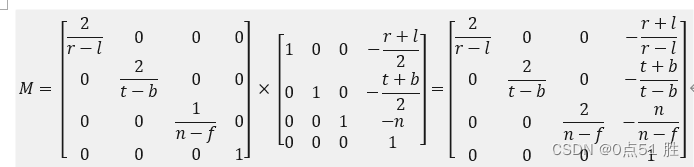
DirectX3D 正交投影学习记录
所谓正交投影变换,就是已知盒状可视空间内任意点坐标(x,y,z),求解垂直投影到xy平面的对应点坐标。 按照这个定义,xyz坐标系本身就是正交坐标系,盒状可视空间内任意点的坐标(x,y,z)投影到(x,y)平面,只要简单地丢弃z坐标…...
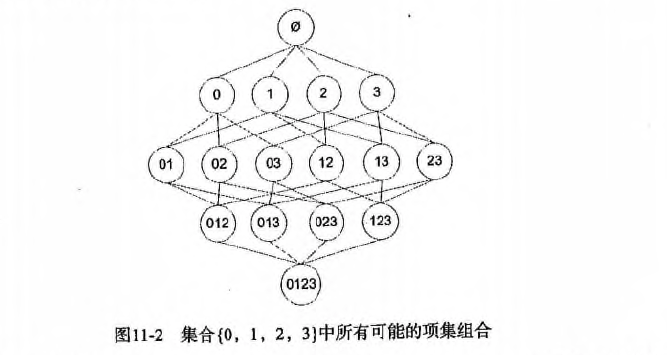
数据挖掘十大算法--Apriori算法
一、Apriori 算法概述 Apriori 算法是一种用于关联规则挖掘的经典算法。它用于在大规模数据集中发现频繁项集,进而生成关联规则。关联规则揭示了数据集中项之间的关联关系,常被用于市场篮分析、推荐系统等应用。 以下是 Apriori 算法的基本概述&#x…...

[蓝桥杯 2022 省 B] 统计子矩阵
题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 11, 最大 NM) 满足子矩阵中所有数的和不超过给定的整数 K。 输入格式 第一行包含三个整数 N, M和 K。 之后 N 行每行包含 M 个整数, 代表矩阵 A。 输出格式 一个整数代表答案。 输入输出样例 输入 #1 3…...

解决在部署springboot项目的docker中执行备份与之相连接的mysql容器命令
文章目录 问题描述解决思路问题解决容器构建mysql客户端安装容器与主机的交互docker中执行 mysqldump 命令解决mysql8密码验证问题解决密码插件警告 问题描述 由于,使用1panel可视化的面板来部署springboot项目,可以很方便地安装和使用mysql,…...

正文Delphi XE Android下让TMemo不自动弹出键盘
用TMemo来显示一段说明文字,可一点Memo,就弹出键盘,找了半天控制键盘的属性,没找到。最后将readOnly设置为True搞定。 如果需要一个form都不显示keyboard,那么可以利用全局变量 VKAutoShowMode来控制,这个全局变量可以有下面三个值…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...