买卖股票的最佳时机 II[中等]
优质博文:IT-BLOG-CN
一、题目
给你一个整数数组prices,其中prices[i]表示某支股票第i天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天出售。返回你能获得的最大利润。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第2天(股票价格= 1)的时候买入,在第3天(股票价格= 5)的时候卖出, 这笔交易所能获得利润= 5 - 1 = 4。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。
总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第1天(股票价格= 1)的时候买入,在第5天 (股票价格= 5)的时候卖出, 这笔交易所能获得利润= 5 - 1 = 4。总利润为4。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为0。
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104
二、代码
【1】动态规划: 定义状态dp[i][0]表示第i天交易完后手里没有股票的最大利润,dp[i][1]表示第i天交易完后手里持有一支股票的最大利润(i从0开始)。考虑dp[i][0]的转移方程,如果这一天交易完后手里没有股票,那么可能的转移状态为前一天已经没有股票,即dp[i−1][0],或者前一天结束的时候手里持有一支股票,即dp[i−1][1],这时候我们要将其卖出,并获得prices[i]的收益。因此为了收益最大化,我们列出如下的转移方程:dp[i][0]=max{dp[i−1][0],dp[i−1][1]+prices[i]}再来考虑dp[i][1],按照同样的方式考虑转移状态,那么可能的转移状态为前一天已经持有一支股票,即dp[i−1][1],或者前一天结束时还没有股票,即dp[i−1][0],这时候我们要将其买入,并减少prices[i]的收益。可以列出如下的转移方程:dp[i][1]=max{dp[i−1][1],dp[i−1][0]−prices[i]}
对于初始状态,根据状态定义我们可以知道第0天交易结束的时候dp[0][0]=0,dp[0][1]=−prices
因此,我们只要从前往后依次计算状态即可。由于全部交易结束后,持有股票的收益一定低于不持有股票的收益,因此这时候dp[n−1][0]的收益必然是大于dp[n−1][1]的,最后的答案即为dp[n−1][0]。
class Solution {public int maxProfit(int[] prices) {if (prices.length < 2) {return 0;}// 思路:通过二维数组表示当前的两种状态 prices[i][0] 表示持有现金 prices[i][1]表示持有股票,每次遍历获取Maxint[][] dp = new int[prices.length][2];// 初始化0dp[0][0] = 0;dp[0][1] = -prices[0];for (int i = 1; i < prices.length; i++) {dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);}return dp[prices.length - 1][0];}
}
注意到上面的状态转移方程中,每一天的状态只与前一天的状态有关,而与更早的状态都无关,因此我们不必存储这些无关的状态,只需要将dp[i−1][0]和dp[i−1][1]存放在两个变量中,通过它们计算出dp[i][0]和dp[i][1]并存回对应的变量,以便于第i+1天的状态转移即可。
class Solution {public int maxProfit(int[] prices) {int n = prices.length;int dp0 = 0, dp1 = -prices[0];for (int i = 1; i < n; ++i) {int newDp0 = Math.max(dp0, dp1 + prices[i]);int newDp1 = Math.max(dp1, dp0 - prices[i]);dp0 = newDp0;dp1 = newDp1;}return dp0;}
}
时间复杂度: O(n)其中n为数组的长度。一共有2n个状态,每次状态转移的时间复杂度为O(1),因此时间复杂度为O(2n)=O(n)。
空间复杂度: O(n)我们需要开辟O(n)空间存储动态规划中的所有状态。如果使用空间优化,空间复杂度可以优化至O(1)。
【2】贪心: 由于股票的购买没有限制,因此整个问题等价于寻找x个不相交的区间(li,ri]使得如下的等式最大化∑i=1xa[ri]−a[li]其中li表示在第li天买入,ri表示在第ri天卖出。同时我们注意到对于(li,ri]这一个区间贡献的价值a[ri]−a[li],其实等价于(li,li+1],(li+1,li+2],…,(ri−1,ri]这若干个区间长度为1的区间的价值和,即a[ri]−a[li]=(a[ri]−a[ri−1])+(a[ri−1]−a[ri−2])+…+(a[li+1]−a[li])因此问题可以简化为找x个长度为1的区间(li,li+1]使得∑i=1xa[li+1]−a[li]价值最大化。
贪心的角度考虑我们每次选择贡献大于0的区间即能使得答案最大化,因此最后答案为ans=∑i=1n−1max{0,a[i]−a[i−1]}其中n为数组的长度。需要说明的是,贪心算法只能用于计算最大利润,计算的过程并不是实际的交易过程。
考虑题目中的例子[1,2,3,4,5],数组的长度n=5,由于对所有的1≤i<n1都有a[i]>a[i−1],因此答案为ans=∑i=1n−1a[i]−a[i−1]=4但是实际的交易过程并不是进行4次买入和4次卖出,而是在第1天买入,第5天卖出。
class Solution {public int maxProfit(int[] prices) {int ans = 0;int n = prices.length;for (int i = 1; i < n; ++i) {ans += Math.max(0, prices[i] - prices[i - 1]);}return ans;}
}
时间复杂度: O(n)其中n为数组的长度。我们只需要遍历一次数组即可。
空间复杂度: O(1)只需要常数空间存放若干变量。
相关文章:

买卖股票的最佳时机 II[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个整数数组prices,其中prices[i]表示某支股票第i天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天出售。返回你能获得…...
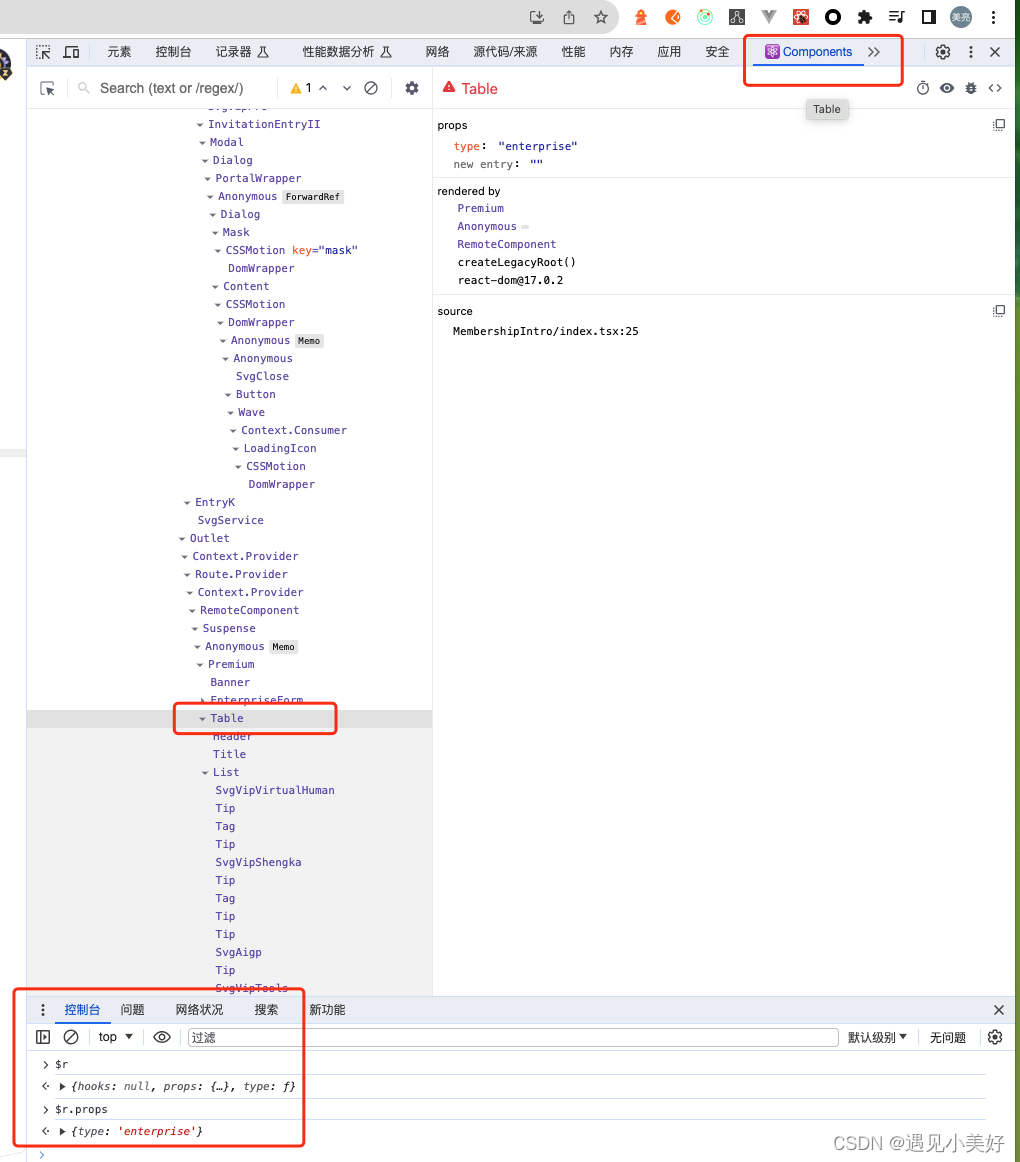
前端开发调试技巧:如何在Component下选中当前插件并且查看当前插件信息
在react开发项目中,在Component下选中组件,然后在控制台输$r 按回车键即可输出该组件信息。例如 $r.props输出该组件的props参数。例子详情见如下截图...

你是否还迷茫要不要学习Linux?
近几年Linux这个词好像很流行,无论是现实工作中,还是在网络信息中均可以听到或者看到有关Linux相关的内容,可以说Linux无处不在。说到这,有人可能会问了,我对Linux比较感兴趣,但是没有接触过Linuxÿ…...
链表)
leetcode(1)链表
# 1. 定义一个链表节点 class ListNode:def __init__(self, val0, next_nodeNone):self.val valself.next_node next_node# 2. 定义一个 node头节点 class LinkedList:def __init__(self):self.head None# 3.链表查找元素 get(index): def get_node(self, index)…...
spring boot Rabbit高级教程
消息可靠性 生产者重试机制 首先第一种情况,就是生产者发送消息时,出现了网络故障,导致与MQ的连接中断。 为了解决这个问题,SpringAMQP提供的消息发送时的重试机制。即:当RabbitTemplate与MQ连接超时后,…...
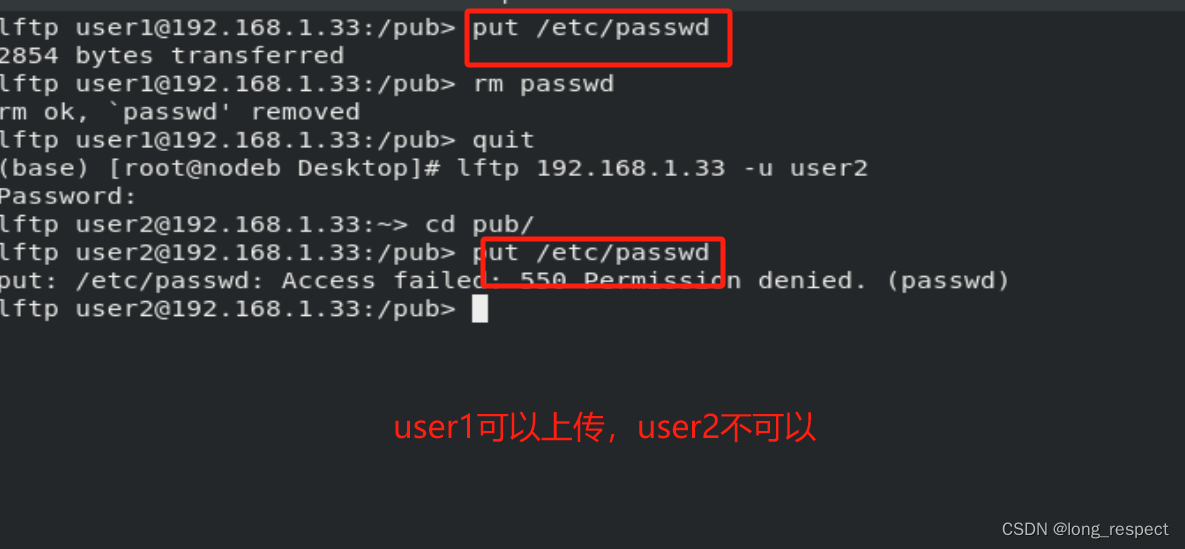
FTP的魅力:构建高效的文件传输基础
1 ftp介绍 1.1 ftp服务器安装 dnf install vsftpd-3.0.3-31.el8.x86_64 -y # 安装ftp服务 systemctl enable --now vsftpd # 启动ftp服务 systemctl stop --now firewalld.service # 关闭防火墙,允许客户端访问anonymous_enableYES #启动匿名用户访问功能1.2 客户…...

70、window11+visual studio2019+共享内存进行数据传输
基本思想:服务端和客户端 写共享内存 #include <windows.h> #include <iostream> using namespace std;HANDLE g_EventRead; // 读信号灯 HANDLE g_EventWrite; // 写信号灯 // 定义共享数据class Writer { public:Writer(const int buf_size, const wchar_t…...

SSTI模板注入(flask) 学习总结
文章目录 Flask-jinja2 SSTI 一般利用姿势SSTI 中常用的魔术方法内建函数 利用 SSTI 读取文件Python 2Python 3 利用 SSTI 执行命令寻找内建函数 eval 执行命令寻找 os 模块执行命令寻找 popen 函数执行命令寻找 importlib 类执行命令寻找 linecache 函数执行命令寻找 subproce…...

最近的工作和生活
大家好,我是记得诚。 聊一聊最近的工作和生活。 不知不觉在管理岗位,快干一年了。技术管理还是比较纯粹,主要还是以解决问题为主,对自己的考验也更大了,要关注更广的技术,也要专注更深的技术细节。 技术…...

第六节:Word中对象的层次结构
《VBA之Word应用》(10178982),是我推出第八套教程,教程是专门讲解VBA在Word中的应用,围绕“面向对象编程”讲解,首先让大家认识Word中VBA的对象,以及对象的属性、方法,然后通过实例让…...

ARJ_DenseNet BMR模型训练
废话不多数,模型训练代码 densenet_arj_BMR.py : import timefrom tensorflow.keras.applications.xception import Xception from tensorflow.keras.applications.densenet import DenseNet169 from tensorflow.keras.preprocessing.image import Im…...

React之Hook
一、是什么 Hook 是 React 16.8 的新增特性。它可以让你在不编写 class 的情况下使用 state 以及其他的 React 特性 至于为什么引入hook,官方给出的动机是解决长时间使用和维护react过程中常遇到的问题,例如: 难以重用和共享组件中的与状态…...

OSG嵌入QT的简明总结2
正文 我之前在这篇博文《OSG嵌入QT的简明总结》中论述了OSG在QT中显示的可视化问题。其中提到官方提供的osgQt项目(地址:https://github.com/openscenegraph/osgQt )很久前已经更新了。但是我一直没有时间同步更新,最近重新尝试了…...
日常中msvcp71.dll丢失怎样修复?分享5个修复方法
在 Windows 系统中,msvcp71.dll 是一个非常重要的动态链接库文件,它承载了许多应用程序和游戏的运行。如果您的系统中丢失了这个文件,那么您可能会遇到无法打开程序、程序崩溃或出现错误提示等问题。本文将介绍 5 个快速修复 msvcp71.dll 丢失…...
【腾讯云TDSQL-C Serverless 产品体验】使用 Python向TDSQL-C添加读取数据实现词云图
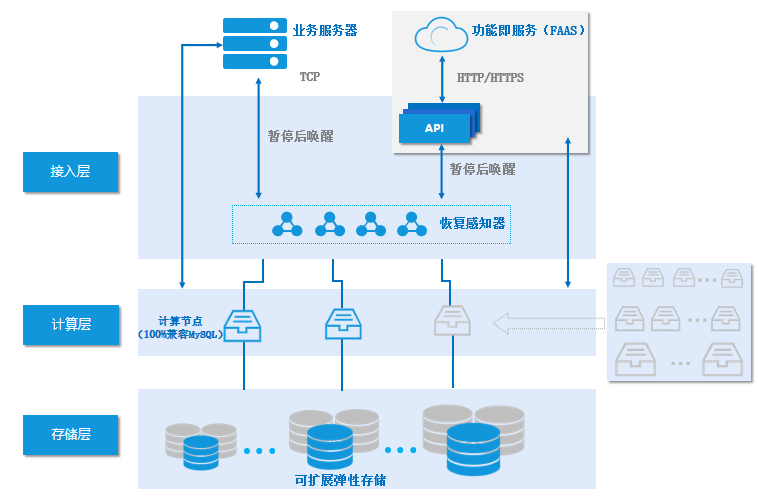
关于TDSQL-C Serverless介绍 TDSQL-C 是腾讯云自主研发的新一代云原生关系型数据库。 它融合了传统数据库、云计算和新硬件技术的优势,100%兼容 MySQL,为用户提供具有极致弹性、高性能、高可用性、高可靠性和安全性的数据库服务。 TDSQL-C 实现了超过百万每秒的高吞吐量,支持…...
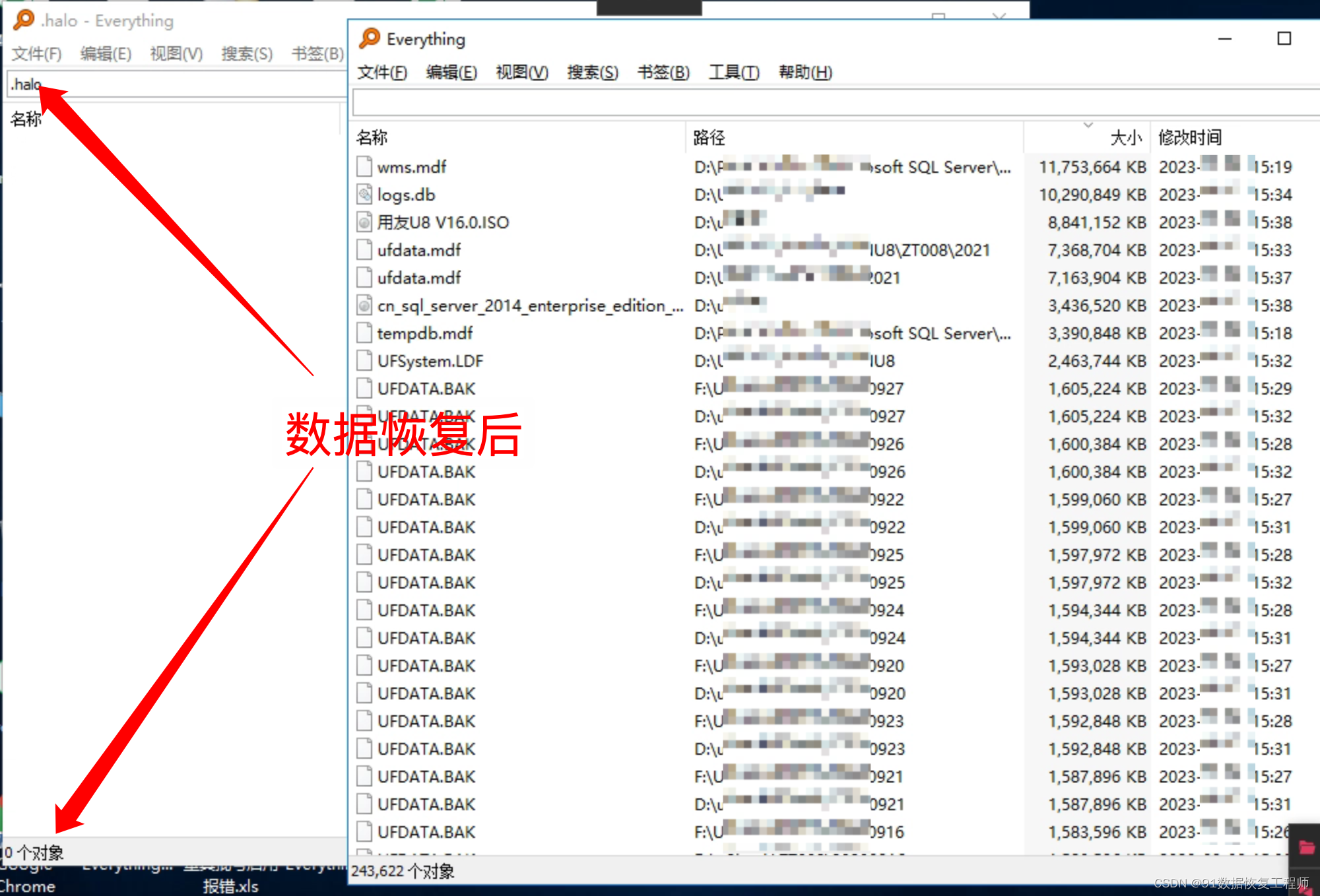
服务器感染了.360、.halo勒索病毒,如何确保数据文件完整恢复?
导言: 数据的安全性至关重要,但威胁不断进化,.360、.halo勒索病毒是其中的令人担忧的勒索软件。本文91数据恢复将深入介绍.360、.halo勒索病毒,包括其威胁本质、数据恢复方法和如何采取预防措施来保护您的数据。 如果受感染的数据…...
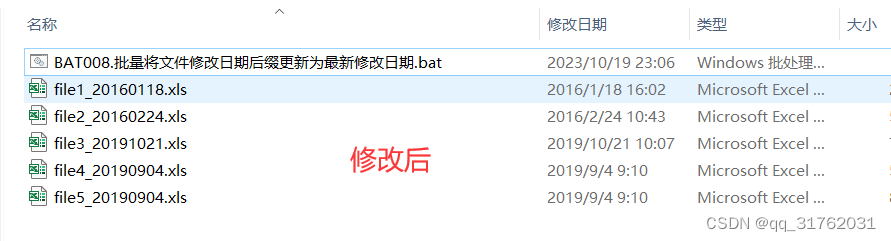
BAT028:批量将文件修改日期后缀更新为最新修改日期
引言:编写批处理程序,实现批量将文件修改日期后缀更新为最新修改日期。 一、新建Windows批处理文件 参考博客: CSDNhttps://mp.csdn.net/mp_blog/creation/editor/132137544 二、写入批处理代码 1.右键新建的批处理文件,点击【…...

Visual Studio C++ 的 头文件和源文件
在Visual Studio C中,头文件(Header Files)和源文件(Source Files)是两种不同的文件类型,用于组织和管理C代码。 头文件(Header Files): 后缀名为.h或.hpp的文件…...

Scrapy框架中的Middleware扩展与Scrapy-Redis分布式爬虫
在爬虫开发中,Scrapy框架是一个非常强大且灵活的选择。在本文中,我将与大家分享两个关键的主题:Scrapy框架中的Middleware扩展和Scrapy-Redis分布式爬虫。这些主题将帮助你更好地理解和应用Scrapy框架,并提升你的爬虫开发技能。 …...

[论文笔记]Sentence-BERT[v2]
引言 本文是SBERT(Sentence-BERT)论文1的笔记。SBERT主要用于解决BERT系列模型无法有效地得到句向量的问题。很久之前写过该篇论文的笔记,但不够详细,今天来重新回顾一下。 BERT系列模型基于交互式计算输入两个句子之间的相似度是非常低效的(但效果是很好的)。当然可以通过…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
