黑白棋(Othello, ACM/ICPC World Finals 1992, UVa220)rust解法
你的任务是模拟黑白棋游戏的进程。黑白棋的规则为:黑白双方轮流放棋子,每次必须让新放的棋子“夹住”至少一枚对方棋子,然后把所有被新放棋子“夹住”的对方棋子替换成己方棋子。一段连续(横、竖或者斜向)的同色棋子被“夹住”的条件是两端都是对方棋子(不能是空位)。如图4-6(a)所示,白棋有6个合法操作,分别为(2,3),(3,3),(3,5),(6,2),(7,3),(7,4)。选择在(7,3)放白棋后变成如图4-6(b)所示效果(注意有竖向和斜向的共两枚黑棋变白)。注意(4,6)的黑色棋子虽然被夹住,但不是被新放的棋子夹住,因此不变白。
 输入一个8*8的棋盘以及当前下一次操作的游戏者,处理3种指令:
输入一个8*8的棋盘以及当前下一次操作的游戏者,处理3种指令:
- L指令打印所有合法操作,按照从上到下,从左到右的顺序排列(没有合法操作时输出No legal move)。
- Mrc指令放一枚棋子在(r,c)。如果当前游戏者没有合法操作,则是先切换游戏者再操作。输入保证这个操作是合法的。输出操作完毕后黑白方的棋子总数。
- Q指令退出游戏,并打印当前棋盘(格式同输入)。
样例:
输入
--------
--------
--------
---WB---
---BW---
--------
--------
--------
W
L
M35
L
Q
输出
[(3, 5), (4, 6), (5, 3), (6, 4)]
W is 4. B is 1
[(3, 4), (3, 6), (5, 6)]
--------
--------
----W---
---WW---
---BW---
--------
--------
--------
解法:
use std::io;enum Cmd {Print,Move(usize, usize),Quit,
}
fn main() {let mut grid: Vec<Vec<char>> = vec![];for _i in 0..8 {let mut buf = String::new();io::stdin().read_line(&mut buf).unwrap();grid.push(buf.trim().chars().collect());}let mut buf = String::new();io::stdin().read_line(&mut buf).unwrap();let mut curplayer = buf.trim().chars().nth(0).unwrap();let mut cmds: Vec<Cmd> = vec![];loop {let mut buf = String::new();io::stdin().read_line(&mut buf).unwrap();buf = buf.trim().to_string();if buf == "L" {cmds.push(Cmd::Print);} else if buf == "Q" {cmds.push(Cmd::Quit);break;} else {let i = buf.chars().nth(1).unwrap().to_digit(10).unwrap();let j = buf.chars().nth(2).unwrap().to_digit(10).unwrap();cmds.push(Cmd::Move(i as usize, j as usize));}}for i in cmds {match i {Cmd::Print => printmoves(&grid, curplayer),Cmd::Move(x, y) => fangzi(&mut grid, &mut curplayer, (x, y)),Cmd::Quit => {printgrid(&grid);break;}}}
}fn fangzi(grid: &mut Vec<Vec<char>>, curp: &mut char, pos: (usize, usize)) {let allmoves = getmoves(grid, *curp);if allmoves.is_empty() {*curp = oposite(*curp);}let newpos = (pos.0 - 1, pos.1 - 1);grid[newpos.0][newpos.1] = *curp;let runs = [(0, -1),(0, 1),(-1, 0),(1, 0),(-1, -1),(1, 1),(-1, 1),(1, -1),];for d in runs {if judge(grid, *curp, newpos, d) {change(grid, *curp, newpos, d);}}let nums = getnums(grid);println!("W is {}. B is {}", nums.0, nums.1);*curp = oposite(*curp);
}fn getnums(grid: &Vec<Vec<char>>) -> (u32, u32) {let mut nums = (0, 0);for i in 0..8 {for j in 0..8 {if grid[i][j] == 'W' {nums.0 += 1;} else if grid[i][j] == 'B' {nums.1 += 1;}}}return nums;
}
fn oposite(p: char) -> char {if p == 'W' {'B'} else {'W'}
}
fn printgrid(grid: &Vec<Vec<char>>) {for line in grid.iter() {println!("{}", line.iter().collect::<String>());}
}
fn getmoves(grid: &Vec<Vec<char>>, curp: char) -> Vec<(usize, usize)> {let mut allmoves: Vec<(usize, usize)> = vec![];let runs = [(0, -1),(0, 1),(-1, 0),(1, 0),(-1, -1),(1, 1),(-1, 1),(1, -1),];for i in 0..8 {for j in 0..8 {//println!("i,j: {},{}", i, j);if grid[i][j] != '-' {continue;}for d in runs {//检查八个方向if judge(grid, curp, (i, j), d) {allmoves.push((i + 1, j + 1));}}}}return allmoves;
}
fn judge(grid: &Vec<Vec<char>>, curp: char, pos: (usize, usize), run: (i32, i32)) -> bool {let mut x = pos.0;let mut y = pos.1;let mut bjiazhu = false;while x > 0 && x < 7 && y > 0 && y < 7 {x = (x as i32 + run.0) as usize;y = (y as i32 + run.1) as usize;if grid[x][y] == '-'{break;}if grid[x][y] == oposite(curp) {bjiazhu = true;}else if bjiazhu {return true;}else {break;}}return false;
}
fn change(grid: &mut Vec<Vec<char>>, curp: char, pos: (usize, usize), run: (i32, i32)) {let mut x = pos.0;let mut y = pos.1;while x > 0 && x < 7 && y > 0 && y < 7 {x = (x as i32 + run.0) as usize;y = (y as i32 + run.1) as usize;if grid[x][y] == oposite(curp) {grid[x][y] = curp;} else {return;}}
}
fn printmoves(grid: &Vec<Vec<char>>, curp: char) {let allmoves = getmoves(grid, curp);if allmoves.is_empty() {println!("No legal move");} else {println!("{:?}", allmoves);}
}
相关文章:

黑白棋(Othello, ACM/ICPC World Finals 1992, UVa220)rust解法
你的任务是模拟黑白棋游戏的进程。黑白棋的规则为:黑白双方轮流放棋子,每次必须让新放的棋子“夹住”至少一枚对方棋子,然后把所有被新放棋子“夹住”的对方棋子替换成己方棋子。一段连续(横、竖或者斜向)的同色棋子被…...

MySQL中如何进行表的优化和压缩?
在MySQL中,可以通过以下方式进行表的优化和压缩: 使用合适的存储引擎(Storage Engine):MySQL提供了多种存储引擎,如InnoDB、MyISAM等。不同的存储引擎在表的优化和压缩方面有不同的特点。例如,I…...
解决方法)
【Java】Jsoup格式化html问题(文本空格折叠等)解决方法
问题说明 Jsoup格式化html文本时,如: Document document Jsoup.parse(html);这里在对html进行格式化的时候会将如下内容: <p> aaa </p>解析成如下格式: <p> aaa </p>即空格折叠问题ÿ…...

Ansible定义各类变量,引用变量方式介绍及注册变量和vars_prompt的用法示例
目录 一.Ansible定义变量 1.用途 2.定义规则 3.变量优先级 二.命令行定义变量 三.定义主机和主机组变量 1.主机变量 (1)内置主机变量 (2)简单示例 2.主机组变量 四.定义playbook变量 1.通过vars表示定义变量ÿ…...

各类证件的版面信息收集
香港身份证的版面分析: 证件页面: 相关的版面信息: 该页面包含香港身份证的信息,可以用于版面分析; 信息来源:香港不同证件说明大汇总|回乡证|居民身份证|护照|永居_手机网易网 台湾通行证号码…...

vueday01——ref响应式
特性:持续监控某个响应式变量的属性名变化,可以使用shallowRef来取消这一特性,只监控对象整体的变化 ref测试代码: <template><div :id"idValue" ref"myDiv">打印obj{{ obj }}</div><…...
SpringBoot集成Redisson操作Redis
目录 一、前言二、基础集成配置(redis单节点)2.1、POM2.2、添加配置文件2.3、添加启动类2.4、添加测试类测试redisson操作redis 一、前言 Redisson 是一个在 Redis 的基础上实现的 Java 驻内存数据网格,Redisson相比较与Jedis和Lettuce来说最…...

整数反转
题目: 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 …...
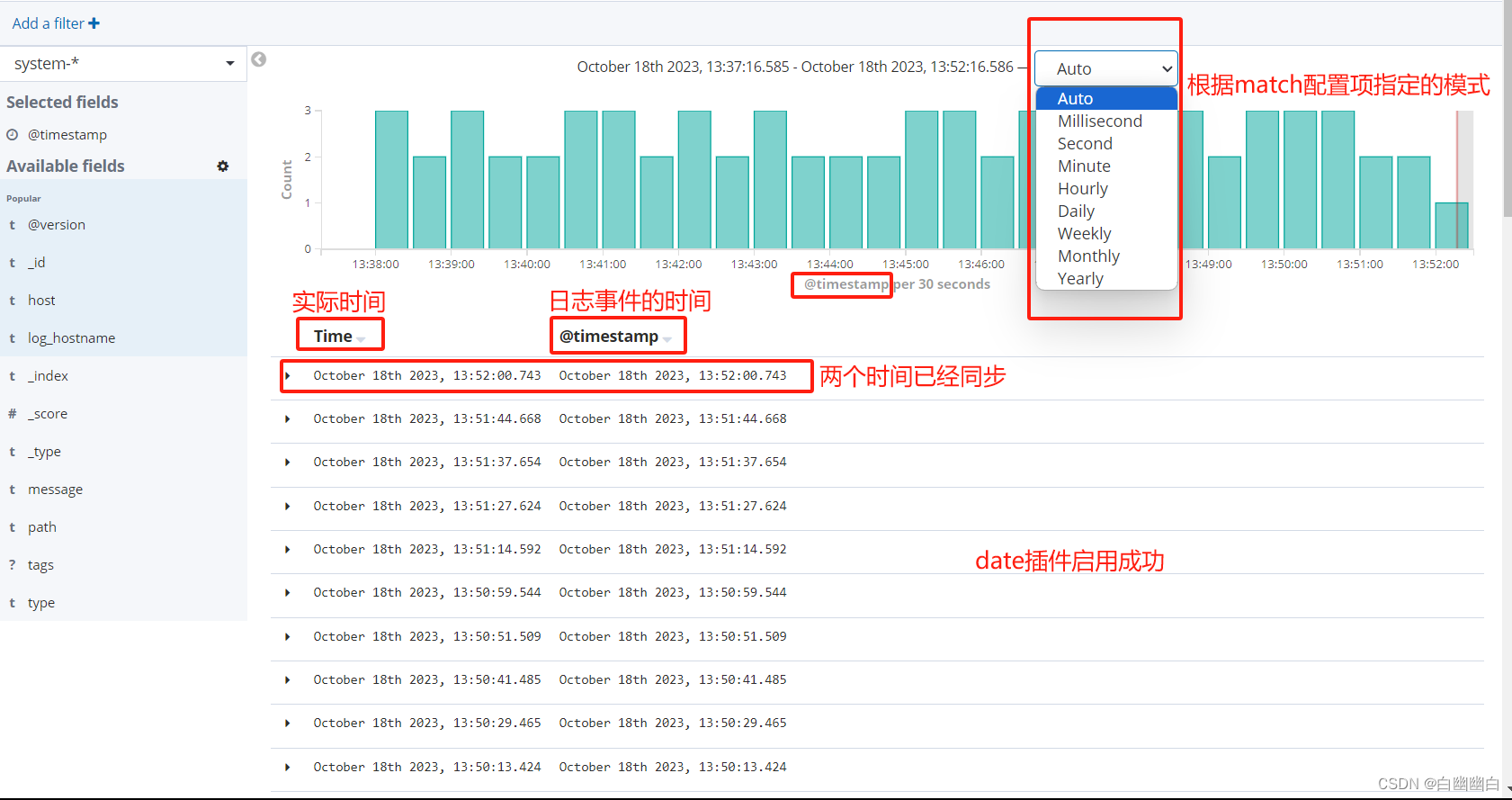
【ELK使用指南 2】常用的 Logstash filter 插件详解(附应用实例)
Logstash filter 一、logstash filter过滤插件的常用模块简介二、grok 正则捕获插件2.1 grok插件的作用2.2 内置正则表达式2.3 自定义正则表达式 三、mutate 数据修改插件3.1 mutate插件的作用3.2 常用的配置选项3.3 mutate插件应用实例 四、multiline 多行合并插件4.1 multili…...
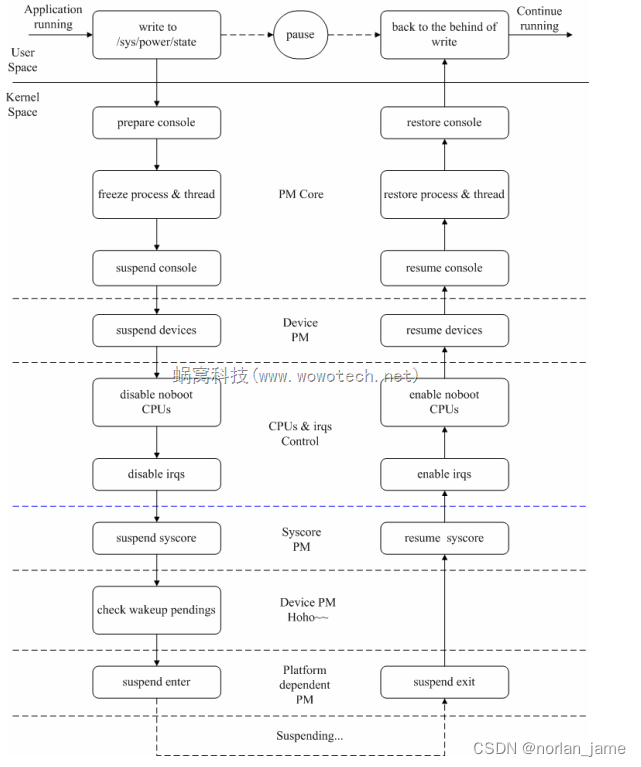
(转)STR 内核做了什么
参考这篇文章: Linux电源管理(6)_Generic PM之Suspend功能 写的很清晰...

fastapi项目结构以及多进程部署
环境: python3.10.x Linux/centos 背景: 最近在用FastApi开发数据统计,并将统计数据返回给前端展示的数据系统。 数据库: mongodb, python包为mongoEngine 项目结构 main.py api middleware router-- __init__.py-- …...
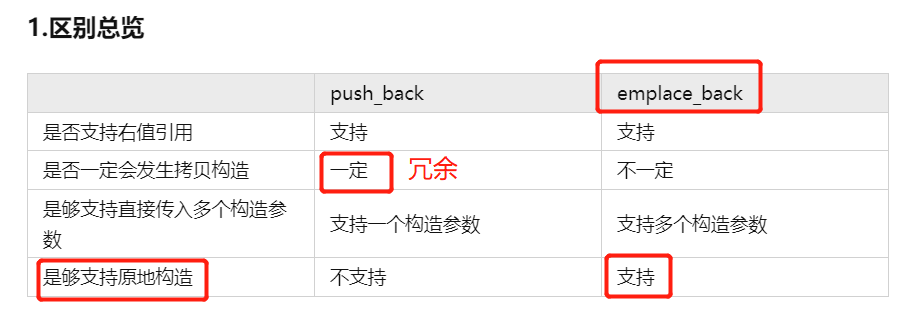
【LeetCode】 412. Fizz Buzz
题目链接 文章目录 Python3 【O(n) O(1)】C.emplace_back() 【C 11 之后】 Python3 【O(n) O(1)】 初始版本 class Solution:def fizzBuzz(self, n: int) -> List[str]:ans []for i in range(1, n1):if i % 5 0 and i % 3 0:ans.append("FizzBuzz")elif i % …...
vector+算法sort与list+sort的效率比较,容易写错的地方原因探析
我写的代码: #include <iostream> using namespace std; #include <vector> #include <list> #include <algorithm> int main() {const int N 10000000;vector<int> v;list<int> l;for (int i 0; i < N; i){v.push_back(…...

iOS——Manager封装网络请求
在之前的项目里,我们都是把网络请求写在viewController的viewDidLoad,而实际中使用的时候并不能这么简单,对于不同的需要,我们需要有不同的网络请求。所以我们可以用单例模式创建一个全局的Manager类,用实例Manager来执…...
【javascript】内部引入与外部引入javascript
创建a.html 内部引入: 外部引入: 创建a.js 注意: 我这里的a.js和a.html是放在同一个目录下,如果a.js放在js的目录下,a.html 调用a.js的时候 <script src"/js/a.js"></script>...
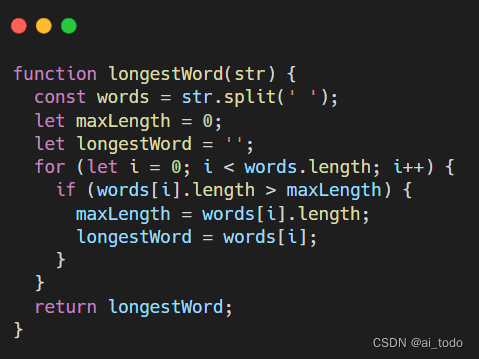
掌握JavaScript的练习之道:十个手写函数让你信手拈来!
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

买卖股票的最佳时机 II[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个整数数组prices,其中prices[i]表示某支股票第i天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天出售。返回你能获得…...
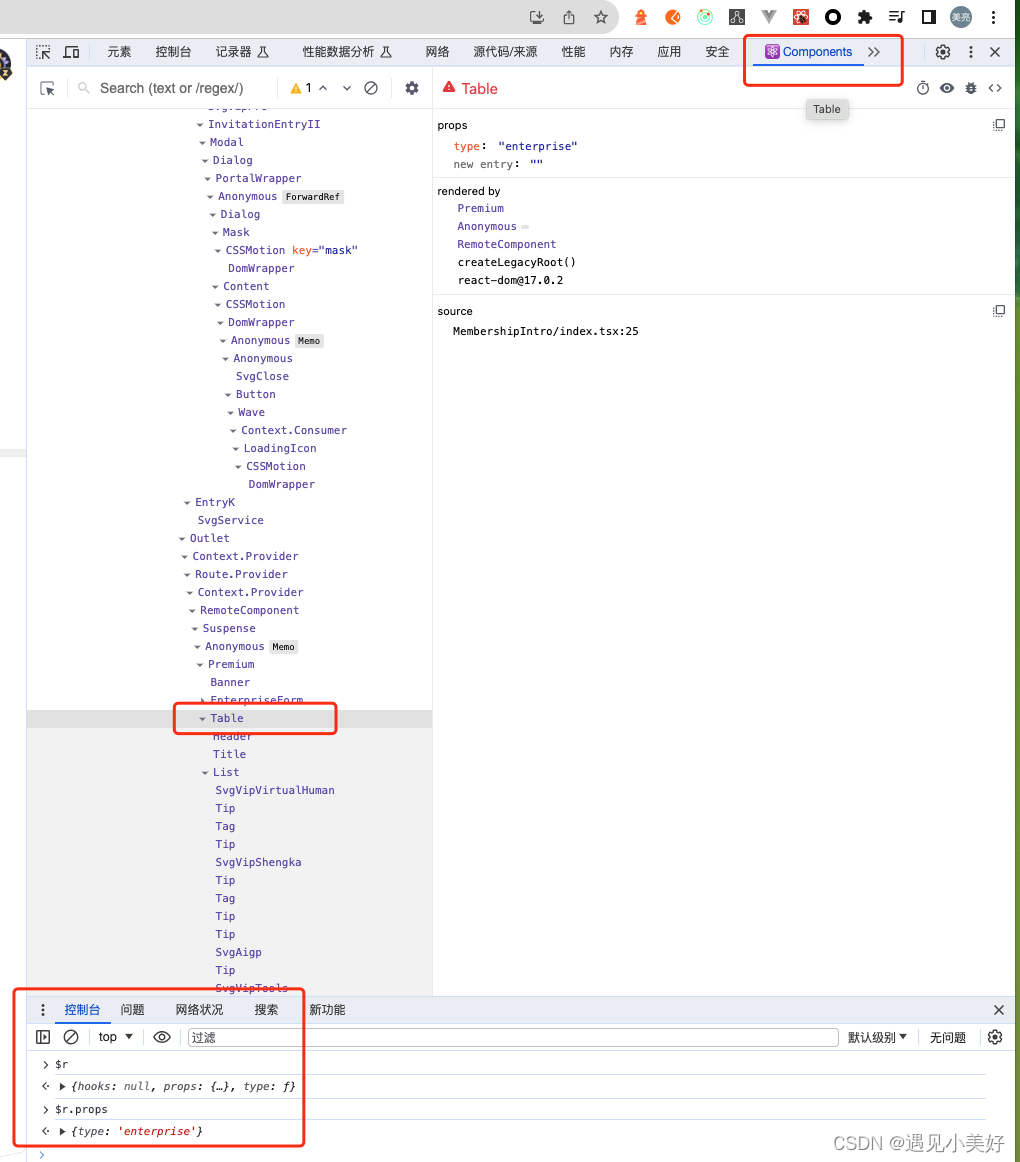
前端开发调试技巧:如何在Component下选中当前插件并且查看当前插件信息
在react开发项目中,在Component下选中组件,然后在控制台输$r 按回车键即可输出该组件信息。例如 $r.props输出该组件的props参数。例子详情见如下截图...

你是否还迷茫要不要学习Linux?
近几年Linux这个词好像很流行,无论是现实工作中,还是在网络信息中均可以听到或者看到有关Linux相关的内容,可以说Linux无处不在。说到这,有人可能会问了,我对Linux比较感兴趣,但是没有接触过Linuxÿ…...
链表)
leetcode(1)链表
# 1. 定义一个链表节点 class ListNode:def __init__(self, val0, next_nodeNone):self.val valself.next_node next_node# 2. 定义一个 node头节点 class LinkedList:def __init__(self):self.head None# 3.链表查找元素 get(index): def get_node(self, index)…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
