leetcode 37. 解数独
编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例 1:

输入:board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:[[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:

提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
题目数据 保证 输入数独仅有一个解
题目链接:解数独
class Solution:def __init__(self):## 需要注意的是 find 需要是一个全局参数,不能是输入 dfs 函数的一个参数self.find = False def dfs(self, board, row, col, square, ss, index):if index == len(ss):self.find = Truereturnr, c = ss[index]if self.find:returnfor i in range(1, 10): if self.find:returnif row[r][i-1] == col[c][i-1] == square[int(r/3)][int(c/3)][i-1] == 0:row[r][i-1], col[c][i-1], square[int(r/3)][int(c/3)][i-1] = 1,1,1board[r][c] = str(i)index += 1self.dfs(board, row, col, square, ss, index)index -= 1if self.find: ## 因为只有一个解, 找到后就不用再回溯了returnboard[r][c] = '.'row[r][i-1], col[c][i-1], square[int(r/3)][int(c/3)][i-1] = 0,0,0def solveSudoku(self, board: List[List[str]]) -> None:"""Do not return anything, modify board in-place instead."""row = [[0]*9 for i in range(9)] # 判断第 i 行有没有 1-9 中的数, 若有对应的 index 则为 1col = [[0]*9 for i in range(9)] # 判断某列square = [[[0]*9 for j in range(3)] for i in range(3)] # 第几个正方形, 有没有某个数ss = []for i in range(9):for j in range(9):if board[i][j] == '.':ss.append([i, j]) ## 存放下需要填充数的位置else:val = int(board[i][j])## 第 i 行,第j 列,以及 第 i/3 行,j/3 列相应的位置值设为 1row[i][val-1] = col[j][val-1] = square[int(i/3)][int(j/3)][val-1] = 1print(ss)self.dfs(board, row, col, square, ss, 0)
相关文章:

leetcode 37. 解数独
编写一个程序,通过填充空格来解决数独问题。 数独的解法需 遵循如下规则: 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图) 数独部分…...

GIT 分支管理办法
GIT 分支管理办法 一. 大型项目分支管理中存在的痛点 大型项目中需求的上线存在很大的不确定性,而且往往存在多版本、多团队、多开发并行的情况。尤其是大型企业对上线分支中编号的管理十分严苛,严禁夹带上线。这时对于开发而言,没有一个好…...

网络代理的多重应用与安全保障
随着互联网的迅速发展,网络代理技术日益受到关注,并在各个领域展现出重要作用。本文将深入探讨Socks5代理、IP代理以及它们在网络安全、爬虫应用和HTTP协议中的多重应用,帮助读者更好地理解和应用这些关键技术。 1. Socks5代理与SK5代理的异…...

C51--简易报警器设计
硬件清单: C52单片机 震动传感器模块 433M无线发射接受模块 继电器模块 高功率喇叭 杜邦线 振动传感器控制灯: 如何知道是否发生震动?震动后的信号表示又是什么? 振动传感器模块产生震动,输出低电平,绿色指…...
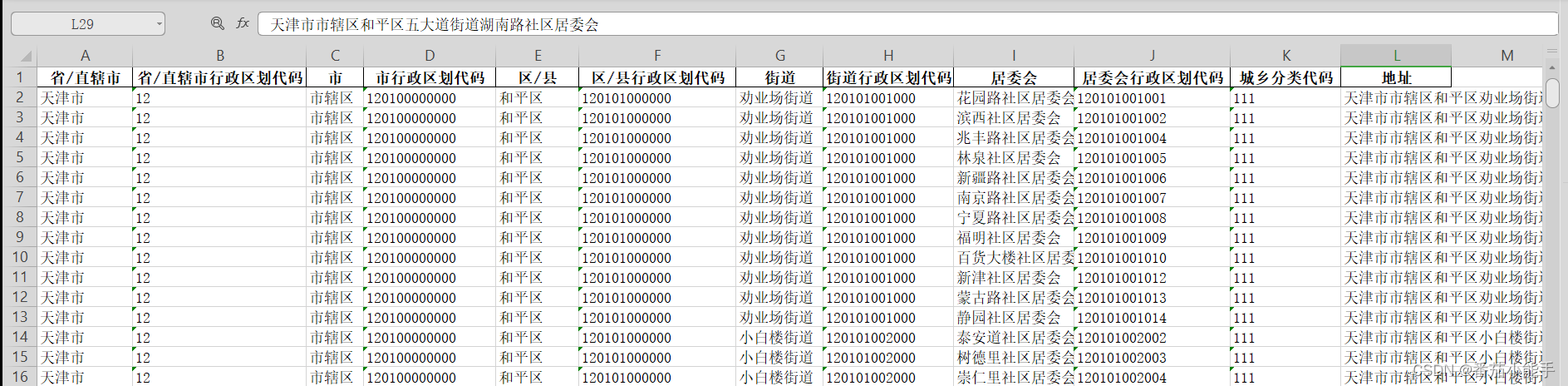
2023年最新全国各省行政区划数据(省-市-区县-乡镇-村)
背景 现实情况,在信息系统开发、电子商务平台、app等等相关软件开发,都会设计到行政区数据联动,这里已经爬好全国各省行政区划数据可供下载。 数据来源 内容为2023年全国统计用区划代码(12位)和城乡分类代码ÿ…...
)
html5 web 按钮跳转方法(及其相关)
html5 web 按钮跳转方法(及其相关) 方法一 <a href"javascript:" οnclick"history.go(-2); ">返回前两页</a> 方法二 <a href"javascript:" οnclick"self.locationdocument.referrer;">返…...

ES6 Generator 函数
Generator 函数是 ES6 提供的一种异步编程解决方案,语法行为与传统函数完全不同。 形式上,Generator 函数是一个普通函数,但是有两个特征。一是,function关键字与函数名之间有一个星号;二是,函数体内部使用…...
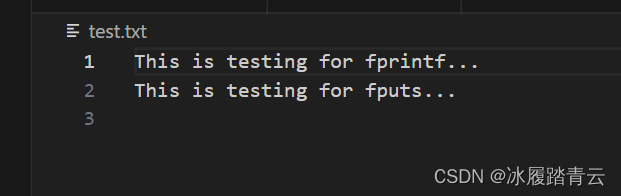
从零开始探索C语言(十二)----预处理器、输入输出及文件读写
文章目录 1. 预处理器1.1 预处理器实例1.2 预定义宏1.3 预处理器运算符1.4 参数化的宏 2. 输入和输出2.1 getchar() & putchar() 函数2.2 gets() & puts() 函数 3. 文件读写3.1 打开文件3.2 关闭文件3.3 写入文件3.4 读取文件3.5 二进制 I/O 函数 4. typedef 和 #defin…...

跨境电商:产业带的深度赋能
近年来,中国跨境电商平台崭露头角,成为推动国内产业带转型升级和出海的新引擎。这一充满活力的领域不仅让中国制造走向世界,也为国内众多产业提供了数字化升级的机会,实现了“小单快反”和按需供应。 专业跨境电商平台如SHEIN和阿…...

09-Vue基础之实现注册页面
个人名片: 😊作者简介:一名大二在校生 🤡 个人主页:坠入暮云间x 🐼座右铭:懒惰受到的惩罚不仅仅是自己的失败,还有别人的成功。 🎅**学习目标: 坚持每一次的学习打卡 文章…...
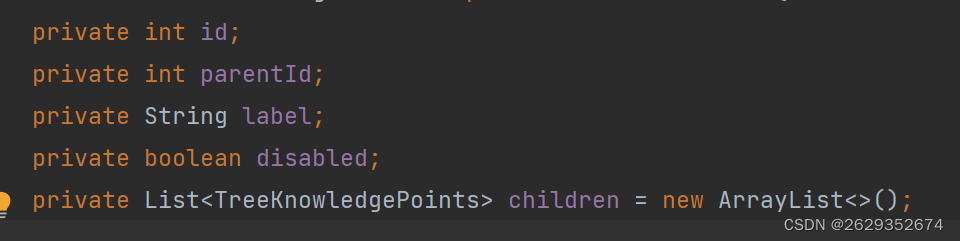
vue 树状结构数据渲染 (java 处理 list ->树状)
树状结构 Element ui https://element.eleme.cn/#/zh-CN/component/tree <el-tree :data"data" :props"defaultProps" node-click"handleNodeClick"></el-tree><script>export default {data() {return {data: [{label: 一级…...

惊艳!这些独特的搜索引擎你都知道吗?
随着互联网的普及和发展,搜索引擎已经成为我们日常获取信息的重要工具。然而,当我们想要寻找一些特定类型的信息时,普通的搜索引擎可能无法满足我们的需求。这时,一些特殊的搜索引擎便能派上用场本。 文将介绍几种常用的特殊搜索引…...

解除OU屏蔽(EBS检查无法直接查询解决)
解除OU屏蔽(EBS检查无法直接查询解决) 具有OU屏蔽的例子 SELECT t.org_id, t.* FROM po.po_headers_all t -- 无屏蔽表,在PL/SQL运行有数据 SELECT t.org_id, t.* FROM apps.po_headers t -- 包含OU屏蔽,在PL/SQL中查询无数据多组织屏蔽原理 1. 在…...
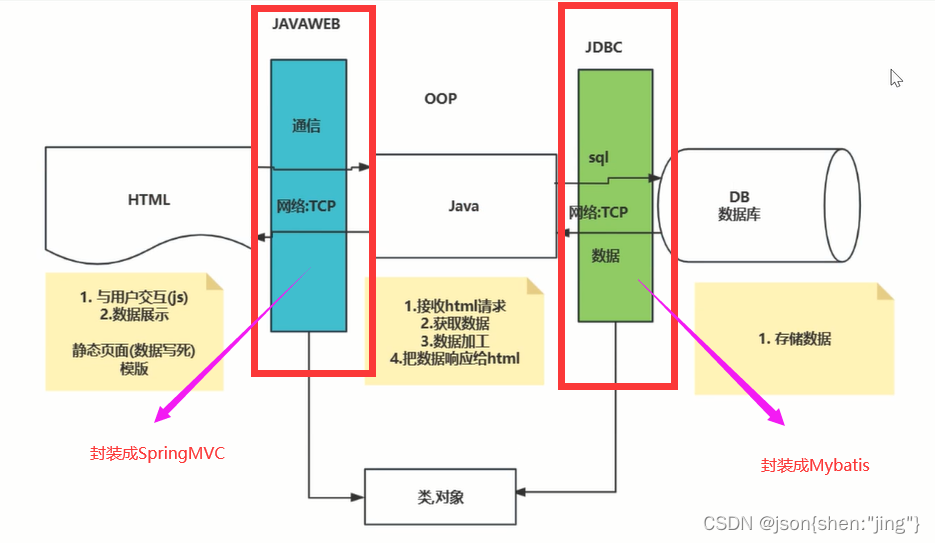
10月8日 Jdbc(1)
jdbc 接口是一个类的父类 java连接数据库, java操作数据库, 把java作为数据库的一个客户端 JDBC是接口,而JDBC驱动才是接口的实现,没有驱动无法完成数据库连接!每个数据库厂商都有自己的驱动,用来连接自己公司的数据库。 …...
SAP 第三方销售/单独采购
一、概述 1. 概念 第三方销售和单独采购都是指接到客户订单后,客户所需产品需要向供应商进行采购,该供应商一般是指外部的供应商,特殊情况下,才可能是集团内部的其他子公司,当是集团内其他子公司时,因为如…...
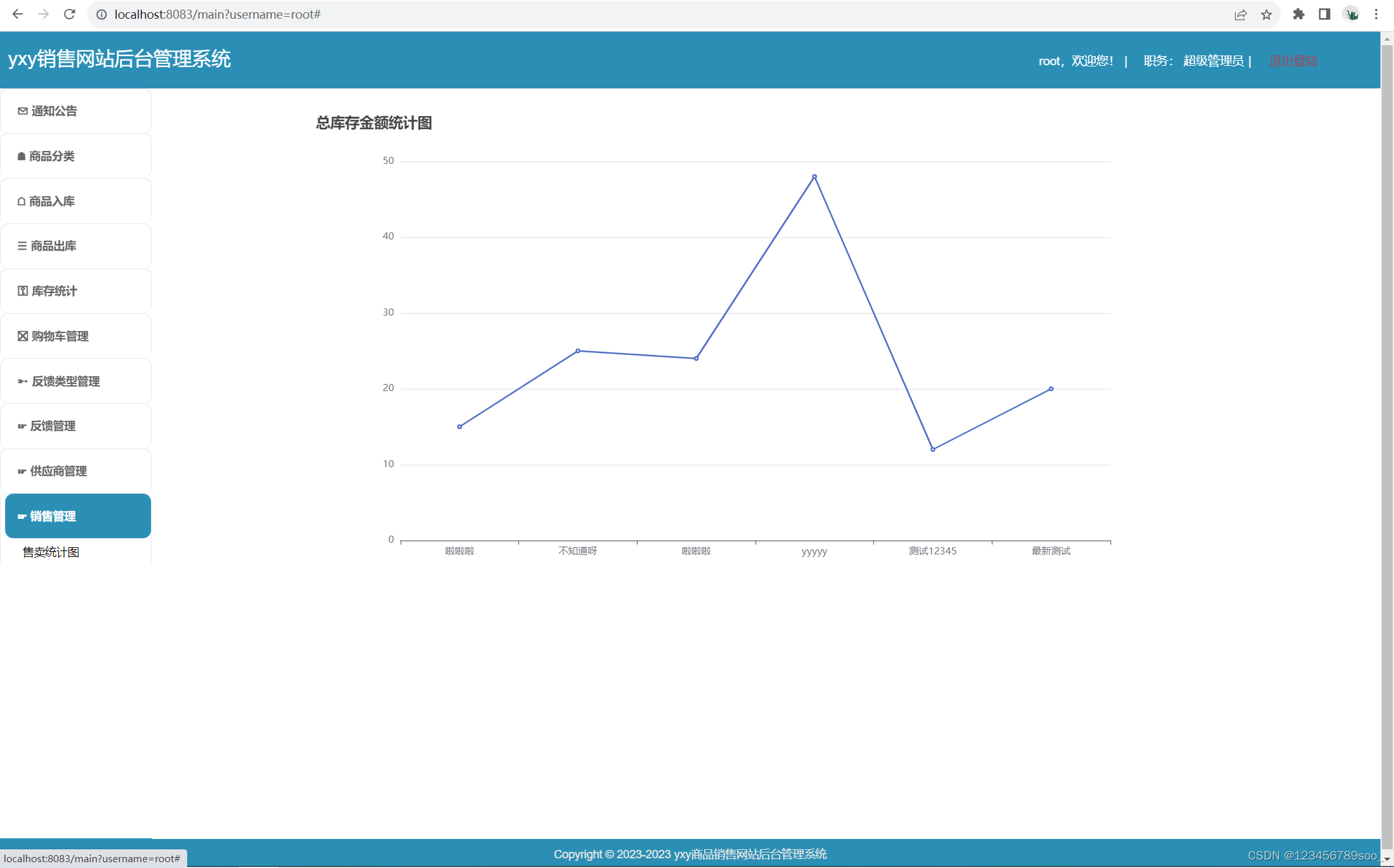
yxy销售网站后台管理系统
springbootmybatisthymeleaf 第一个练习的项目就是小商品零售平台后台管理系统,但是当时由于业务不熟练,需求分析先不做好,导致在开发的过程中出现了很多问题。 这次首先把需求确定,详细的做好前期准备工作,再来进行…...

【vSphere 8 自签名证书】企业 CA 签名证书替换 vSphere Machine SSL 证书Ⅲ—— 颁发自签名证书
目录 博文摘要5. 使用 Microsoft 证书颁发机构颁发自签名 SSL 证书5.1 登录MADCS5.2 申请证书5.3 选择证书类型5.4 提交CR5.5 下载 Base 64 编码的证书5.6 导出 CA 证书(1)打开 cachain.p7b(2)进入证书导出导向(3&…...
:MapReduce之ETL清洗案例)
Hadoop3教程(十九):MapReduce之ETL清洗案例
文章目录 (121)ETL数据清洗案例参考文献 (121)ETL数据清洗案例 ETL,即Extract-Transform-Load的缩写,用来描述数据从源端,经过抽取(Extract)、转换(transfor…...
)
数据库设计阶段-架构真题(五十七)
下面关于联合需求计划JRP叙述,不正确的是()。 JRP是一种相对成本较高但十分有效的需求获取方法在讨论期间尽量避免使用专业术语JRP的主要目的是对需求进行分析和验证在JRP实施之前,应制定详细的议程,并严格遵照议程进…...
python控制Windows桌面程序自动化模块uiautomation
github仓库地址:GitHub - yinkaisheng/Python-UIAutomation-for-Windows: (Donot use 3.7.6,3.8.1):snake:Python 3 wrapper of Microsoft UIAutomation. Support UIAutomation for MFC, WindowsForm, WPF, Modern UI(Metro UI), Qt, IE, Firefox, Chrome ... uiaut…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
