当前位置：首页 > news >正文

手写一个PrattParser基本运算解析器3: 基于Swift的PrattParser的项目概述

news 2025/12/15 22:04:50

点击查看基于Swift的PrattParser项目

PrattParser项目概述

前段时间一直想着手恶补 编译原理 的相关知识, 一开始打算直接读大学的 编译原理, 虽然内容丰富, 但是着实抽象难懂. 无意间看到B站的熊爷关于普拉特解析器相关内容, 感觉是一个非常好的切入点.所以就写了基于Swift版本的 PrattParser.

下面是我整理的项目中各个类以及其中函数的作用.

更加具体的请查看 PrattParser解释器项目类与函数

接下来, 我把整个项目UML图发出来, 大家可以借鉴查看.

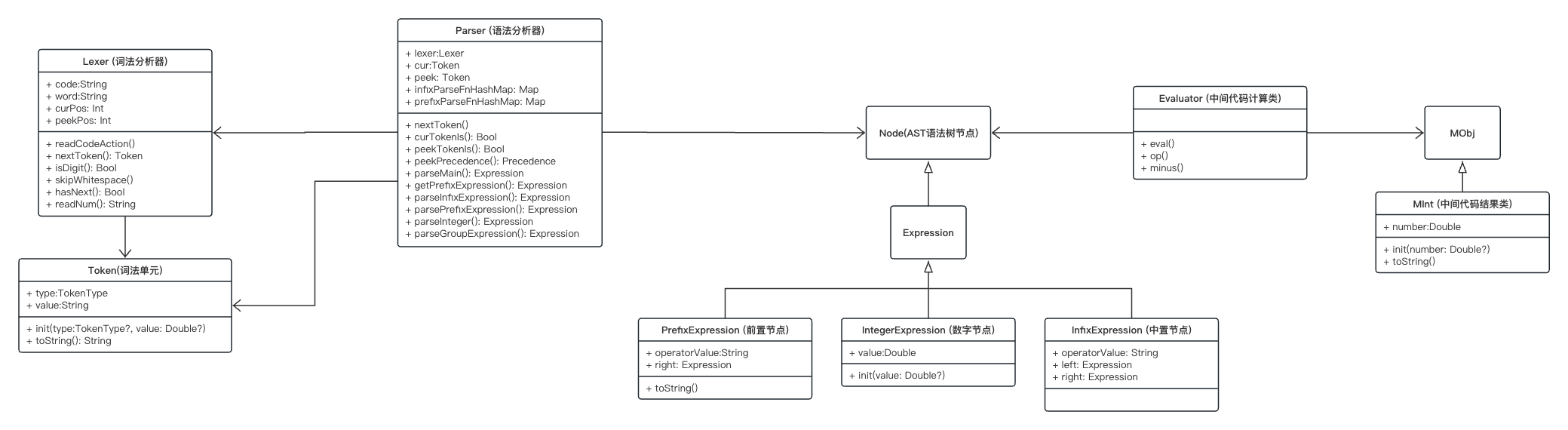
更加具体的请查看 PrattParser的Swift项目UML图

接下来, 我就以 词法分析 、语法分析 、 中间代码生成 三部分逐步来说明一下这个基于Swift的PrattParser项目

词法分析

词法分析的核心类是 Lexer, 输入的原始代码字符串 code, 输出的是一组词法单元 Token.

在词法分析器 Lexer 中, 核心函数就是 nextToken, nextToken函数职责一共有两个职责.

去除代码格式化的逻辑, 例如, 去除 空格 换行 等等. 这一步主要是通过调用 skipWhitespace() 函数实现的.

public func skipWhitespace() {while (hasNext()) {if (word == " " || word == "\t" || word == "\n" || word == "\r")  {readCodeAction();} else {break}}
}

读取数学符号与数字并且生成 词法单元Token

switch(word) {
case "+" :token = PrattParser.Token(TokenType.PLUS, "+")break
case "-" :token = PrattParser.Token(TokenType.MINUS, "-")break
case "*" :token = PrattParser.Token(TokenType.ASTERISK, "*")break
case "/" :token = PrattParser.Token(TokenType.SLASH, "/")break
case "(" :token = PrattParser.Token(TokenType.LPAREN, "(")break
case ")" :token = PrattParser.Token(TokenType.RPAREN, ")")break
case "^" :token = PrattParser.Token(TokenType.HAT, "^")break
case nil :token = PrattParser.Token(TokenType.EOF, "")break
default:if (isDigit(word)) {let num: String = readNum();token = PrattParser.Token(TokenType.NUM, num);return token;} else {throw LexerError.lexerError(message: "Lexer error")}
}

生成词法单元函数 nextToken 的整体逻辑流程图如下所示. 基本涉及了词法分析器 Lexer 的所有函数.

这里要补充的一点的就是由于数学符号大部分是单个字符, 例如 + - * / ( ), 这个读取直接生成即可. 但是数字可能是有多位的, 所以生成的过程需要通过循环一直查找. 在该项目中的代码实现中读取数字字符的逻辑代码主要存在于 readNum 函数中.

public func readNum() -> String {var num: String = ""while (isDigit(word)) {num += word ?? ""readCodeAction()}return num;
}

生成数字函数 readNum 的整体逻辑流程图如下所示.

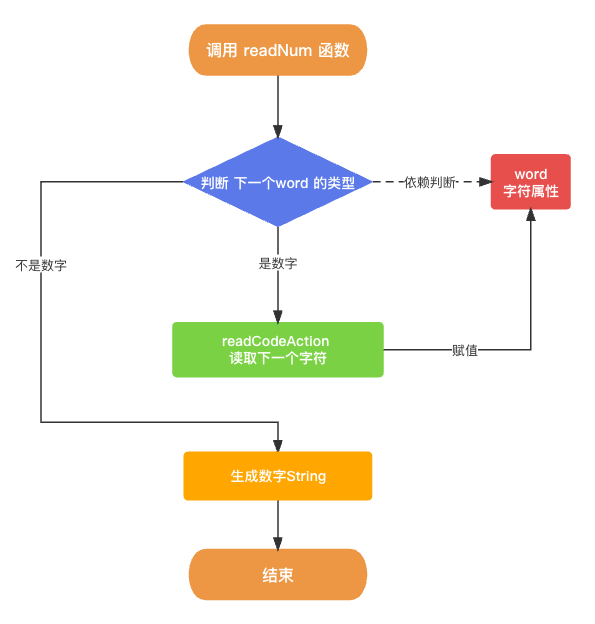
在该项目中, 词法分析器Lexer 的外部驱动力是 语法分析器Parser, 也就是说语法分析器Parser一直在调用 Lexer 的 nextToken 函数从而不断地生成词法单元 Token.

语法分析

在 词法分析 模块, 我们了解到了 词法分析器Lexer 会为 语法分析器Parser 提供源源不断生成的词法单元 Token.

语法分析器Parser 则会这些词法单元 Token根据符号的优先级生成一颗 AST语法树.

在 语法分析器Parser 生成 AST语法树 的过程中, 其入口函数是 parseMain(), 核心函数是 parseExpression(), 具体代码如下所示.

func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 生成前置节点, 获取左节点var leftExpression: Expression? = getPrefixExpression(funcName);// 能递归的原因 判断下一个词法单元是否是EOF, 判断下一个词法单元的优先级是否大于当前的优先级while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}//读取下一个词法单元nextToken();// 生成中置节点, 更新AST语法树leftExpression = parseInfixExpression(leftExpression);}return leftExpression
}

由于递归过程比较复杂, 我整理了一下整体的逻辑流程图.

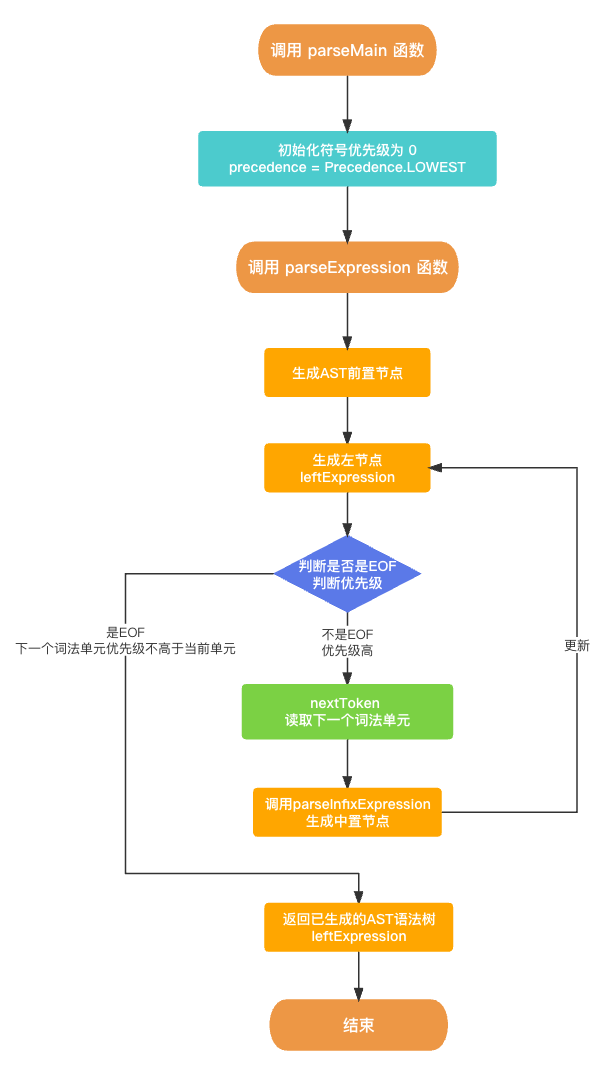
当我们看到上一个图的时候, 我们会诧异, 说好的递归过程在哪呢? 其实递归过程主要隐藏在生成中置节点函数 parseInfixExpression() 中, 由于 parseExpression() → parseInfixExpression() → parseExpression() → .... 的调用关系会最终产生递归效果.

在中置节点生成函数parseInfixExpression中, 右节点的生成依然会依赖 parseExpression(), 这也就递归产生的驱动力.

// 中置节点生成函数
func parseInfixExpression(_ left: Expression?) -> Expression? {let infixExpression = InfixExpression();infixExpression.left = left;infixExpression.operatorValue = cur?.value;let precedence: Precedence = Precedence.getPrecedence(cur?.type);nextToken();// 右节点的生成是递归产生的驱动力infixExpression.right = parseExpression(precedence);return infixExpression
}

中置节点生成函数parseInfixExpression的逻辑流程图如下所示.

粗略的说了大致的流程, 接下来, 我们就详情的说一下具体的执行流程.

具体的以 1 + 4 - 3 和 1 + 2 * 3 两个数学运算为示例.

`1 + 4 - 3` 的AST语法树构建过程

强烈建议大家一边项目断点, 一边对照该模块的流程!!!

整体还是以 parseMain() 为入口, 初始过程中会传入一个最低的优先级(Precedence.LOWEST)用于驱动整个AST语法树的构建. 当然了, 这时候词法单元读取模块也已经准备就绪了.
```
// 构建AST树主入口
public func parseMain() -> Expression? {return parseExpression(Precedence.LOWEST);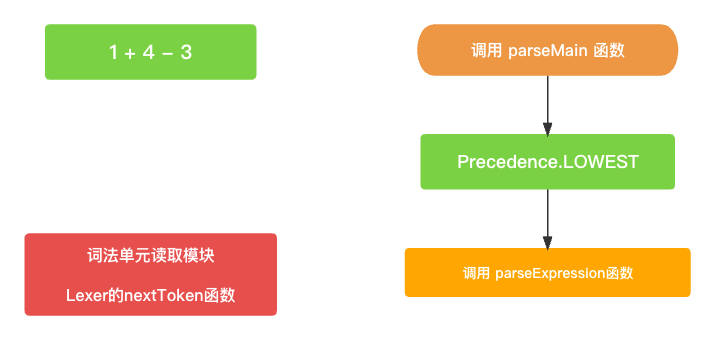
}
```

通过 parseMain 函数进入的 parseExpression() 函数中, 首先找的就是前置节点, 通过 词法单元读取模块 获取到第一个词法单元 1. 并且生成根据 前置节点的类型 生成 数字类型的AST前置节点. getPrefixExpression 就不过多叙述了, 比较简单.

let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];
if (funcName == nil) {print("未找到AST节点构建函数名称")return nil
}
// 获取左节点
var leftExpression: Expression? = getPrefixExpression(funcName);

func getPrefixExpression(_ funcName: String?) -> Expression? {switch(funcName) {case "parseInteger" :return parseInteger()case "parsePrefixExpression":return parsePrefixExpression()case "parseGroupExpression":return parseGroupExpression()default:return nil}
}

func parseInteger() -> Expression? {let number = Double(cur?.value ?? "0")let integerExpression = IntegerExpression(value: number)return integerExpression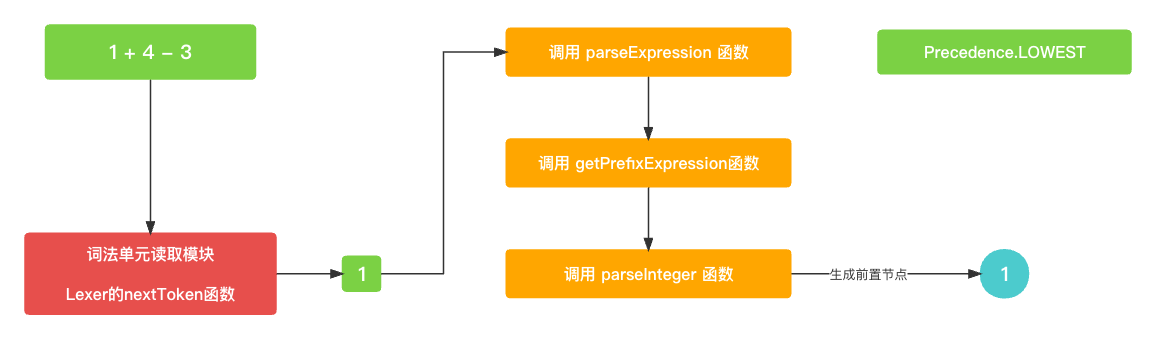
}

紧接着就是去找到中置节点, 这时候通过peekPrecedence() 知道下一个词法单元为 +, 优先级较高, 满足优先级条件. 进入递归循环. 然后nextToken()读取下一个词法单元 +, 然后通过调用 parseInfixExpression() 尝试生成AST中的中置节点.

while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}nextToken();leftExpression = parseInfixExpression(leftExpression);
}

在中置节点生成函数 parseInfixExpression() 中, 由于当前的词法单元为 + , 左节点为前置节点 1, 我们可以直接构建出这一部分的AST语法树.
```
let infixExpression = InfixExpression();
infixExpression.left = left;
infixExpression.operatorValue = cur?.value;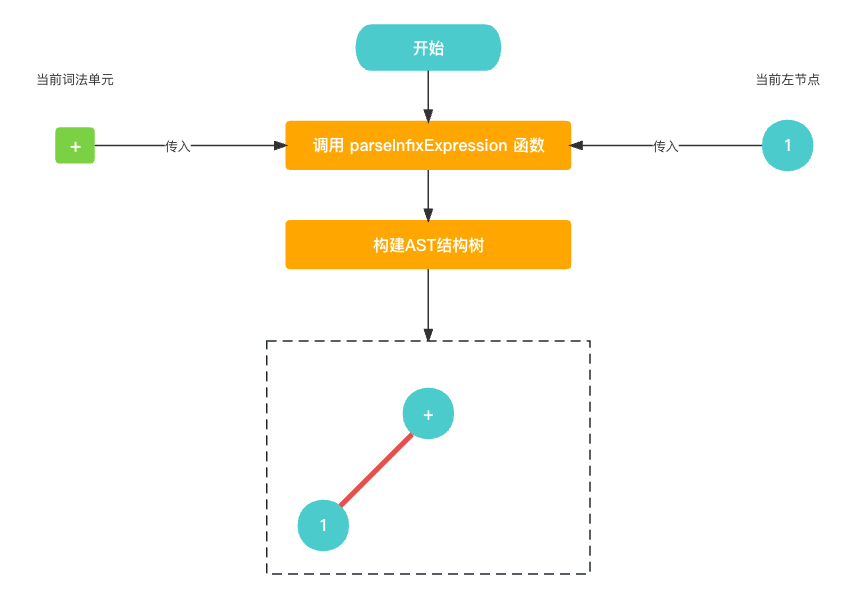
```
构建了中置节点的值和左节点, 我们尝试用 parseExpression() 递归的形式找到 +的中置节点 的右节点, 我们需要先读取当前 + 的优先级(Precedence.SUM), 然后读取下一个节点.
```
let precedence: Precedence = Precedence.getPrecedence(cur?.type);
nextToken();
infixExpression.right = parseExpression(precedence);
```

在 parseExpression() 寻找 +的中置节点 的右节点, 首先, 就是获取 数字词法单元4 生成前置节点, 然后往后读取, 发现是 符号词法单元- 优先级与当前 符号词法单元+ 的优先级相同, 所以就不进入while循环, 故+的中置节点 的右节点是 前置节点4.

// 参数优先级为 Precedence.SUM
func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 获取左节点, 生成 数字前置节点 4var leftExpression: Expression? = getPrefixExpression(funcName);//  - 与 + 的优先级相同不进入while循环while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}nextToken();leftExpression = parseInfixExpression(leftExpression);}// 返回 数字前置节点 4return leftExpression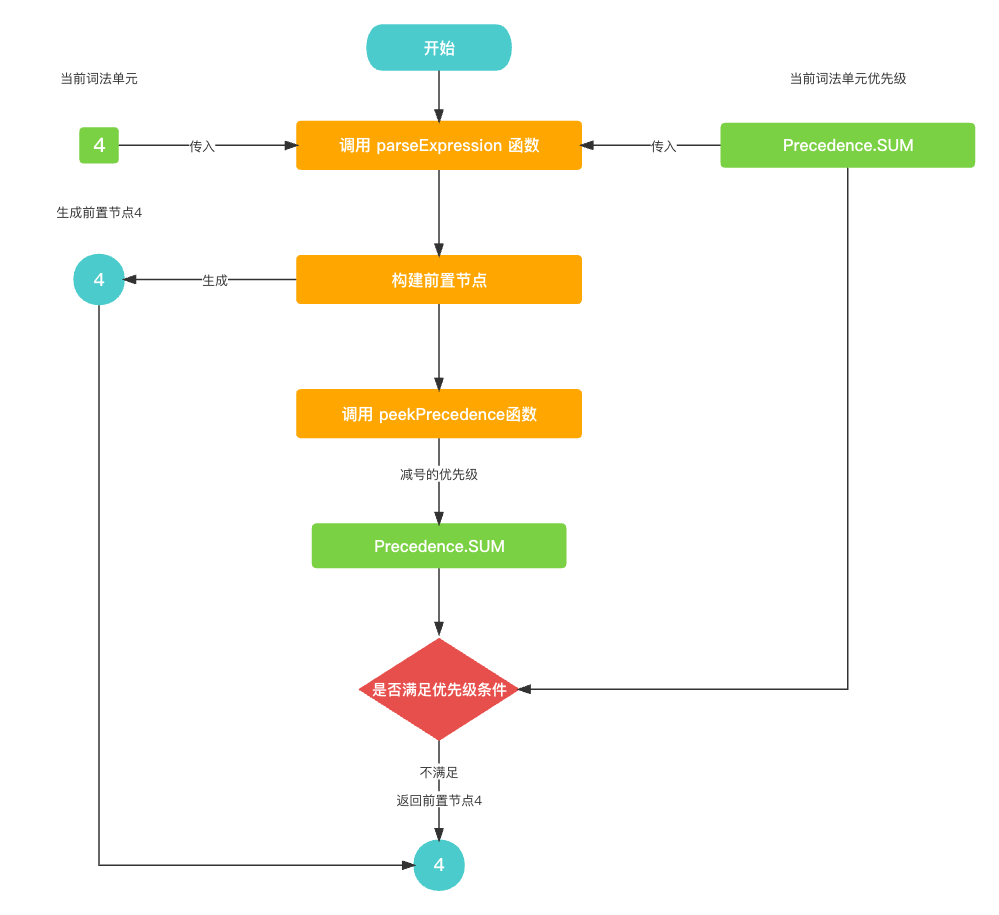
}

这时候, 对于 中置节点+号 的AST语法树就构建完成了, 如图所示.

然后外部又一次进行while循环, 这次找到的是 ➖ 号, 然后把 中置节点+号的AST语法树 整体作为➖中置节点的左节点传入.

// 这时候再次进入 减号➖ 的循环中
while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}// 读取词法单元减号➖nextToken();// 这里的leftExpression是 加号➕ 的AST语法树//   +//  ╱ ╲// 1   4leftExpression = parseInfixExpression(leftExpression);
}

在 ➖ 号的中置节点 构建过程中, 中置节点+号的AST语法树 作为其左节点, - 作为其值, 右节点继续通过parseExpression()寻找.

let infixExpression = InfixExpression();
// 这里的left是 加号➕ 的AST语法树
//   +
//  ╱ ╲
// 1   4
infixExpression.left = left;
infixExpression.operatorValue = cur?.value;

和 中置节点+号 寻找右节点的逻辑是一样. 我们继续尝试用 parseExpression() 递归的形式找到 -的中置节点 的右节点, 我们需要先读取当前 - 的优先级(Precedence.SUM), 然后读取下一个节点.
```
let precedence: Precedence = Precedence.getPrecedence(cur?.type);
nextToken();
infixExpression.right = parseExpression(precedence);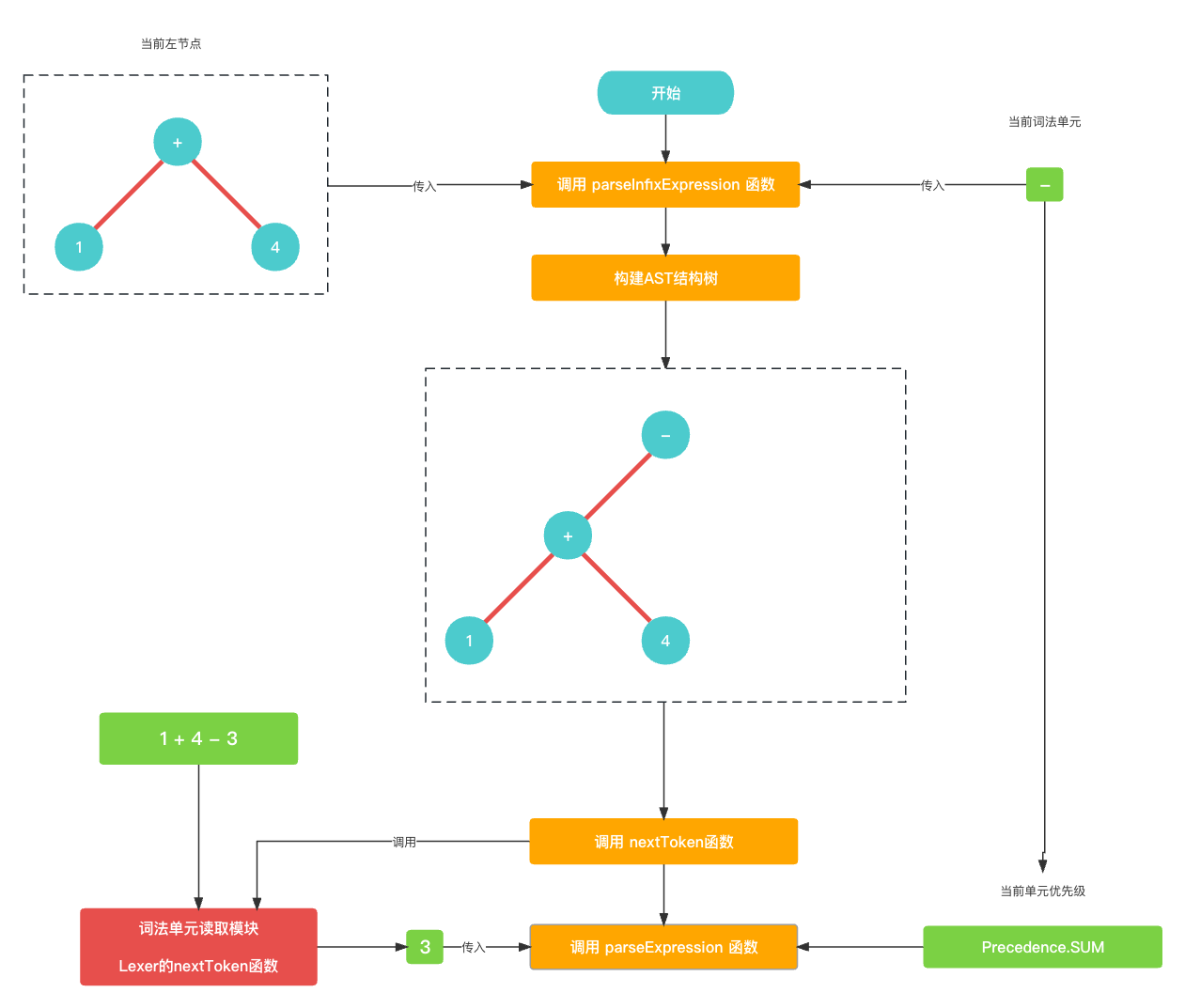
```

这次在 parseExpression() 就很简单了, 我们先构建了前置节点3 然后往后查找过程发现是结束词法单元EOF, 我们直接返回 前置节点3 即可.

func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 构建 前置节点3var leftExpression: Expression? = getPrefixExpression(funcName);// peekToken == EOF 不满足while循环条件while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}nextToken();leftExpression = parseInfixExpression(leftExpression);}// 返回 前置节点3return leftExpression
}

返回了右节点之后, 我们就直接构建 ➖减号的AST语法树, 这里看一下整体的构建过程.
➖减号的AST语法树 然后再次返回整体的循环, 发现当前的词法节点以及全部循环完成了, 所以就跳出了while循环, 返回最终的AST语法树. 这里就把整理的流程贴图如下所示.
所以1 + 4 - 3 形成的AST语法树是这样的. 如下图所示.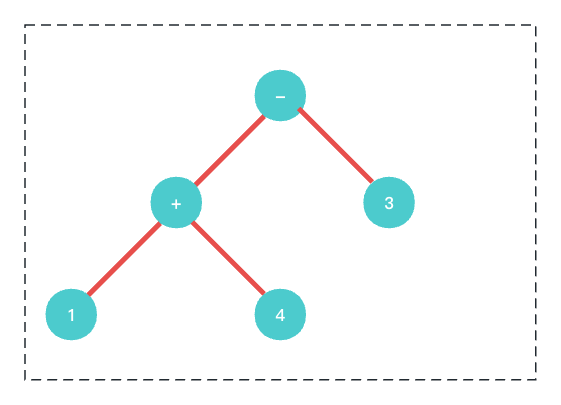

`1 + 2 * 3` 的AST语法树构建过程

相比于 1 + 4 - 3 的最终结果来说, 1 + 2 * 3 其中 乘法* 一定要比 加法+ 优先级高. 最终应该是这样的 1 + (2 * 3) . 也就是我们预想的AST语法树应该如下所示.

接下来, 我们就一起看一下 1 + 2 * 3 的AST语法树构建逻辑.

对于 1 + 2 * 3 一直到加法的中置节点寻找右节点之前的逻辑都是与先前一样的. 这里直接贴图了, 就不过多叙述代码了.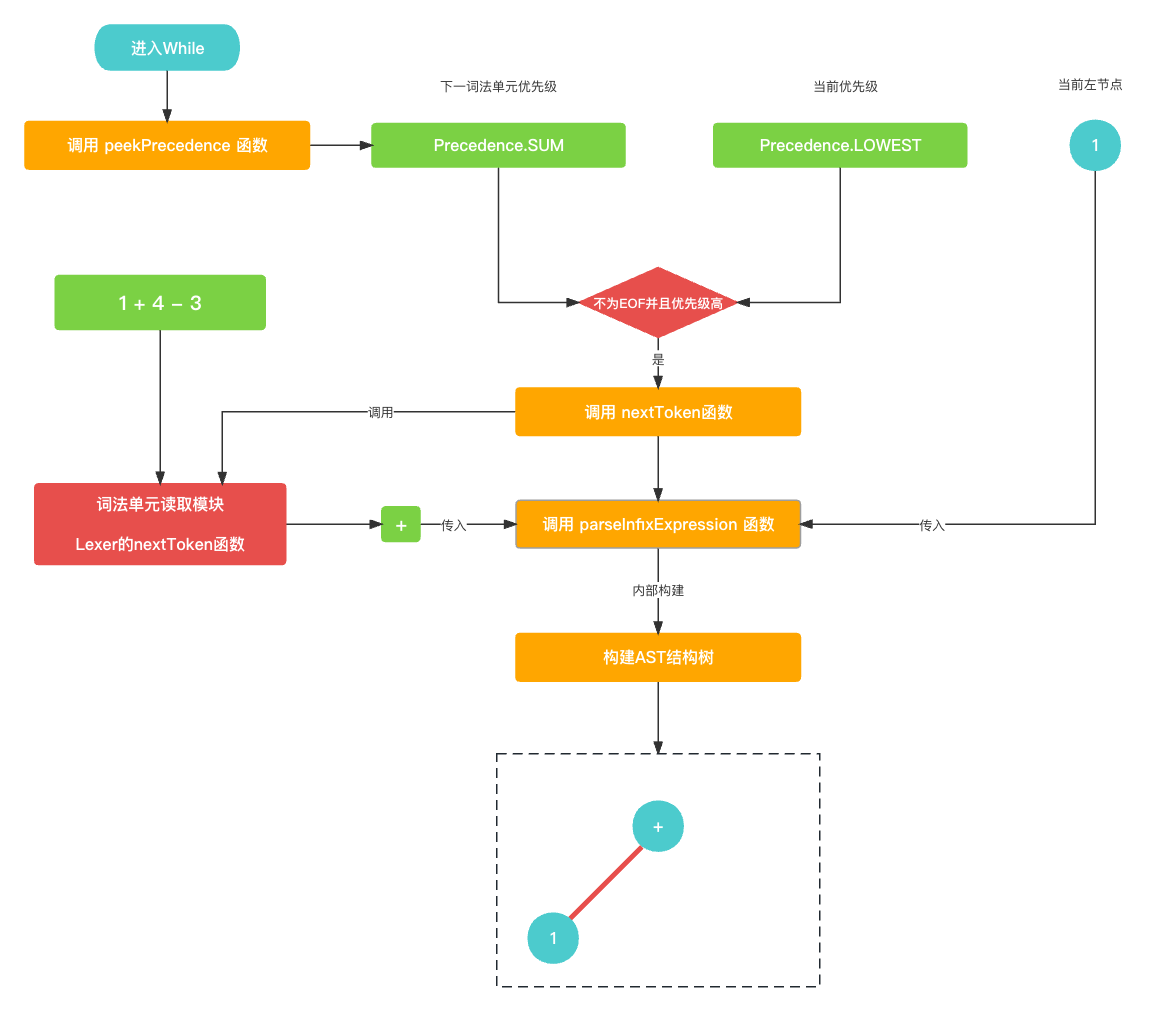

接下来, 对于 中置节点加号+ 需要通过 parseExpression() 去寻找它自身的右节点. 这时候准备工作也要做好, 读取下一个词法单元2, 获取当前加号的优先级(Precedence.SUM).

// 当前加号的优先级为 Precedence.SUM
let precedence: Precedence = Precedence.getPrecedence(cur?.type);
// 下一个词法单元为 词法单元2
nextToken();
// 寻找 中置节点加号+ 的 右节点
infixExpression.right = parseExpression(precedence);

然后, 在 parseExpression() 就是先构建 前置节点2, 然后查看后一个词法单元, 发现是 乘法符号*, 乘法符号的优先级(Precedence.PRODUCT) 要比加法符号的优先级(Precedence.SUM) 要高, 所以进入while循环中. 继续构建关于 中置节点乘法* 的相关AST语法树.

// 当前优先级是 Precedence.SUM, 当前Token是 2
func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 构建左节点 前置节点2var leftExpression: Expression? = getPrefixExpression(funcName);// 乘法符号的优先级比当前加号优先级高, 正常进入while循环while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}// 读取下一个词法单元 乘法符号*nextToken();// 生成乘法符号的中置节点并且更新leftExpressionleftExpression = parseInfixExpression(leftExpression);}return leftExpression
}

let infixExpression = InfixExpression();
infixExpression.left = left;
infixExpression.operatorValue = cur?.value;
// 当前的乘法符号 的AST语法树
//   *
//  ╱ ╲
// 2   ?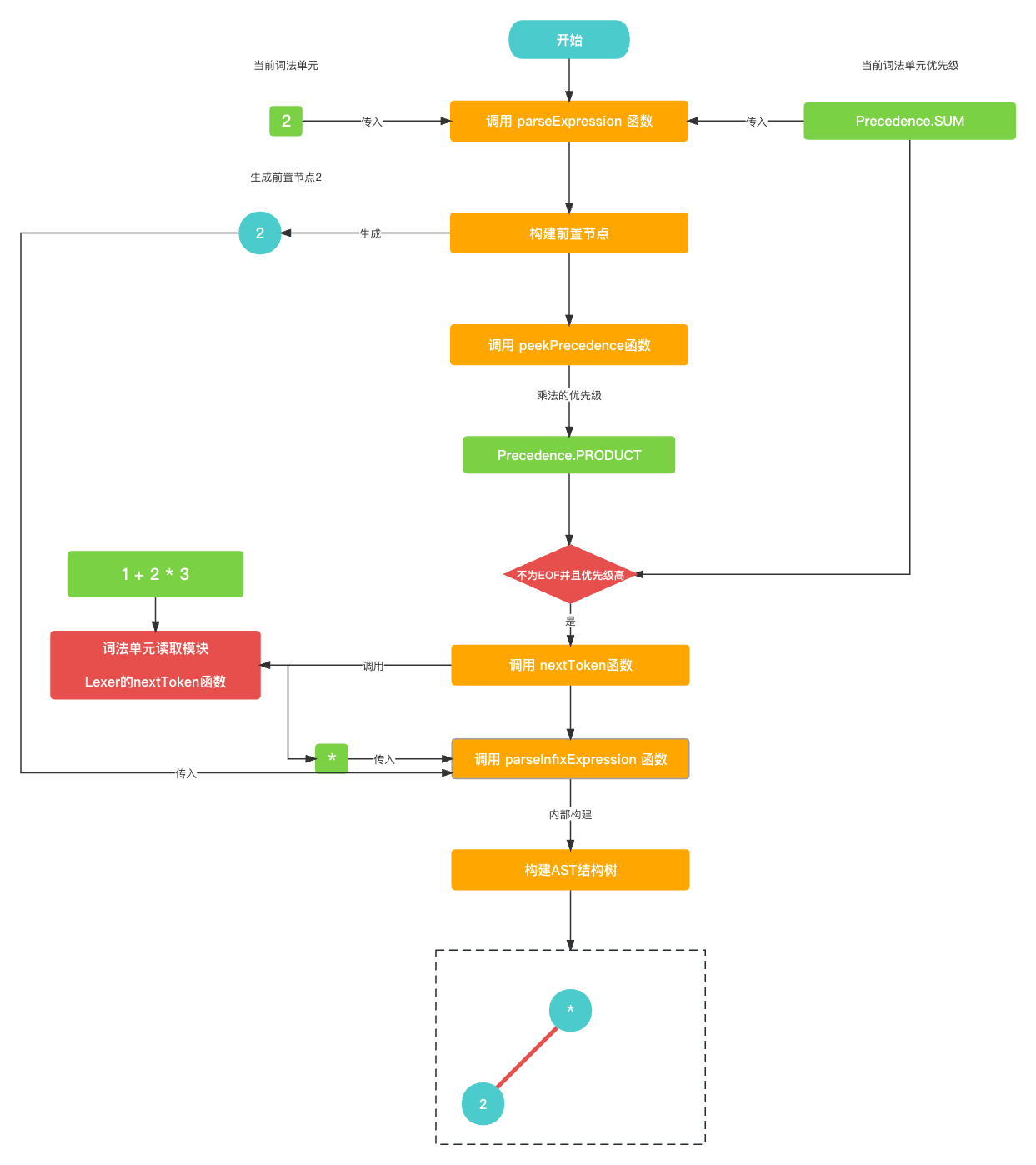

紧接着, 就是寻找乘法AST语法树的右节点, 仍然是通过 parseExpression() 函数, 传入的Token则是 词法单元3, 乘法符号的优先级为 Precedence.PRODUCT,

// 乘法符号的优先级为 Precedence.PRODUCT
let precedence: Precedence = Precedence.getPrecedence(cur?.type);
// 读取词法单元3
nextToken();
infixExpression.right = parseExpression(precedence);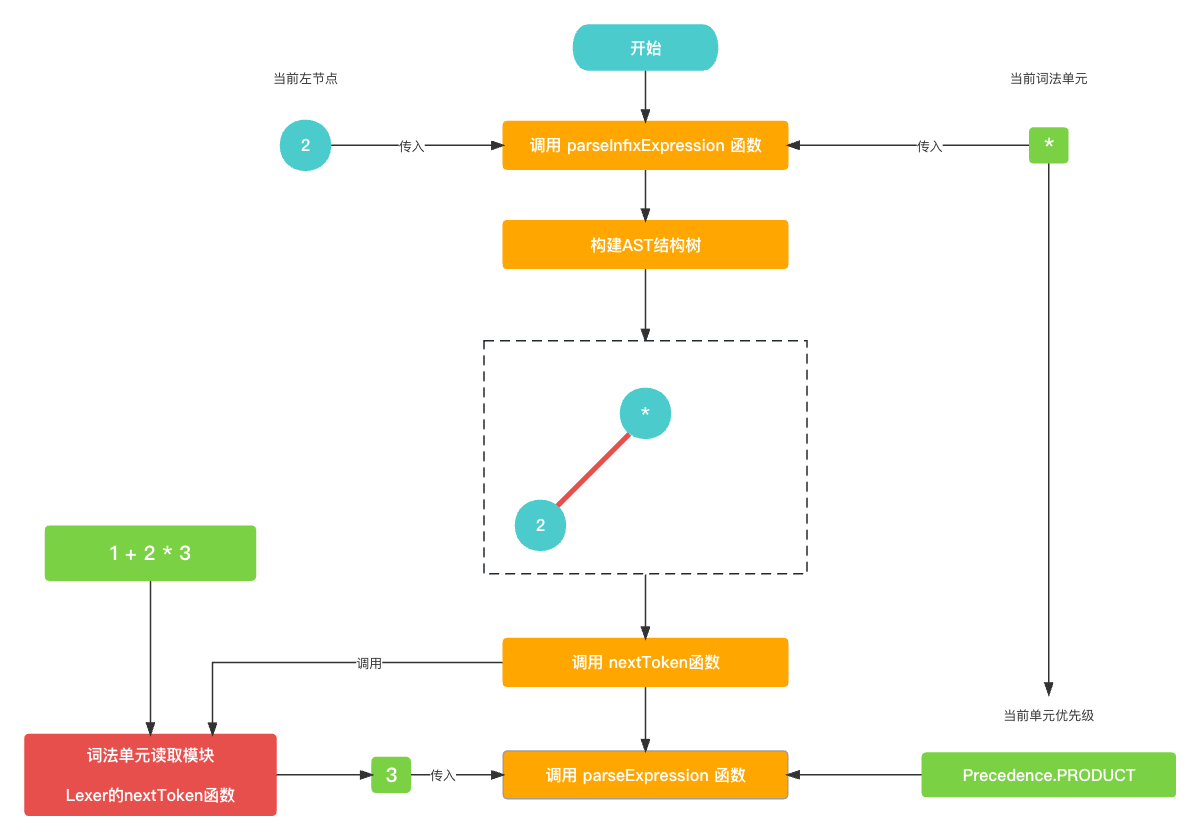

在这次乘法符号寻找右节点的 parseExpression() 中, 首先构建了 前置节点3, 由于看到下一个节点是 结束词法单元EOF, 所以不进入循环, 直接返回 前置节点3.

func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 构建 前置节点3var leftExpression: Expression? = getPrefixExpression(funcName);// peekToken == EOF 不满足while循环条件while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}nextToken();leftExpression = parseInfixExpression(leftExpression);}// 返回 前置节点3return leftExpression
}

这时候也就构建完成了乘法的AST语法树部分了. 我们一起看一下整体的乘法符号的AST语法树构建过程.

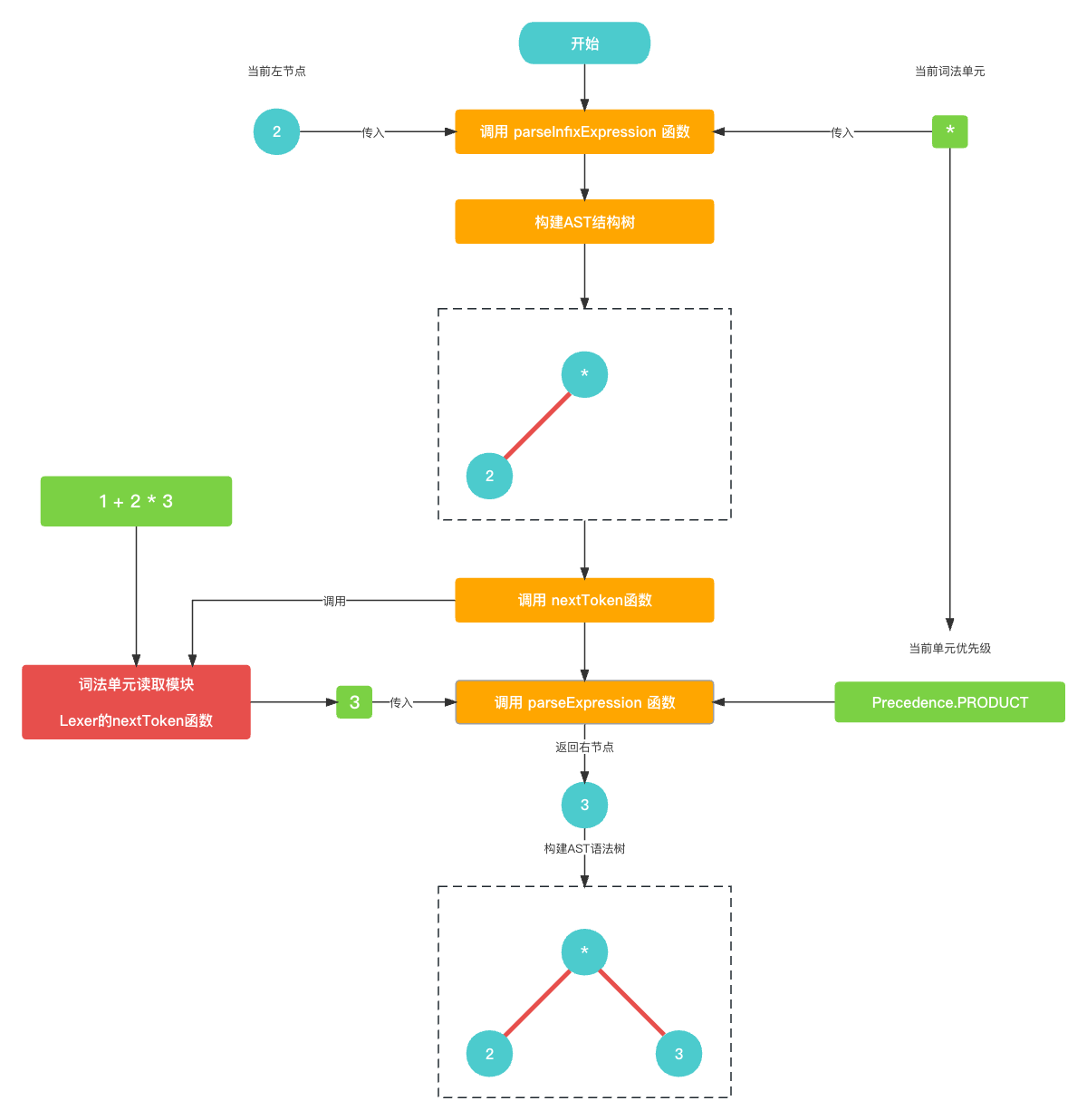
由于已经遍历到了最后(遇到了EOF), 紧接着就跳出了加法符号寻找右节点的parseExpression()过程中的while循环. 并把乘法符号的AST语法树作为加法符号的右节点进行了添加.

// 这里是加法符号寻找右节点的递归方法
// 当前优先级是 Precedence.SUM, 当前Token是 2
func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 构建左节点 前置节点2var leftExpression: Expression? = getPrefixExpression(funcName);// 乘法符号的优先级比当前加号优先级高, 正常进入while循环while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}// 读取下一个词法单元 乘法符号*nextToken();// 生成乘法符号的中置节点并且更新leftExpressionleftExpression = parseInfixExpression(leftExpression);}// 最终 leftExpression 是乘法符号的AST语法树//   *//  ╱ ╲// 2   3return leftExpression
}

上述代码就是下图中红色的parseExpression()的内部过程.

最后返回初始那一层由 parseMain() 进入的 parseExpression() 过程, 也是已经遍历到了最后(遇到了EOF), 跳出循环, 返回最终的AST语法树.

// 这里是由 `parseMain()` 进入的 `parseExpression()`
func parseExpression(_ precedence: Precedence) -> Expression? {let funcName: String?  = prefixParseFnHashMap[cur?.type ?? TokenType.None];if (funcName == nil) {print("未找到AST节点构建函数名称")return nil}// 构建左节点 前置节点1var leftExpression: Expression? = getPrefixExpression(funcName);// 构建了加法的AST语法树之后, 就退出了循环while (!peekTokenIs(TokenType.EOF) && precedence.rawValue < peekPrecedence()?.rawValue ?? 0) {let infixParseFnName: String?  = infixParseFnHashMap[peek?.type ?? TokenType.None];if (infixParseFnName == nil) {print("未找到AST节点构建函数名称")return leftExpression;}nextToken();leftExpression = parseInfixExpression(leftExpression);}// 最终 leftExpression 是加法符号的AST语法树//   +//  ╱ ╲// 1   *//    ╱ ╲//   2   3return leftExpression
}

这样我们对于数学表达式的 1 + 2 * 3 的 AST语法树构建过程就有整体的了解,最终输出的AST语法树如下所示.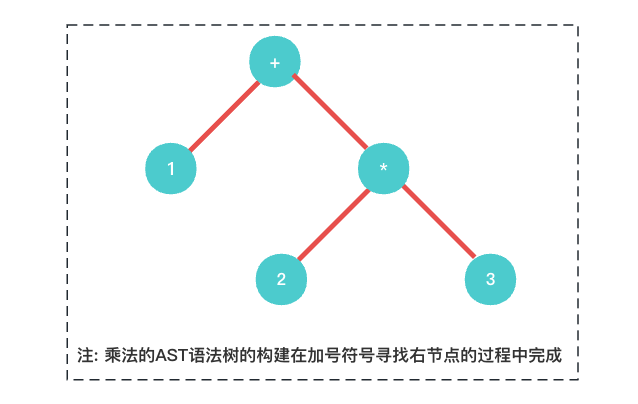

中间代码生成与验证

对于上面的 1 + 4 - 3 和 1 + 2 * 3 的两个示例, 我们对PrattParser构建AST语法树的过程有了大体的了解.

接下来就是中间代码生成过程(其实不太准确, 大体模拟吧~), 我们会直接输入一个结果对象(MInt), 模拟中间代码的生成.

中间代码生成是由 Evaluator 来实现的, 其主要作用就是解析AST语法树, 生成中间代码结果对象(MInt). 这部分也是很简单, 主要是通过 eval() 函数来递归解析AST语法树, 然后通过 op() 函数进行各种数学计算. 整体的计算也是由递归完成的.

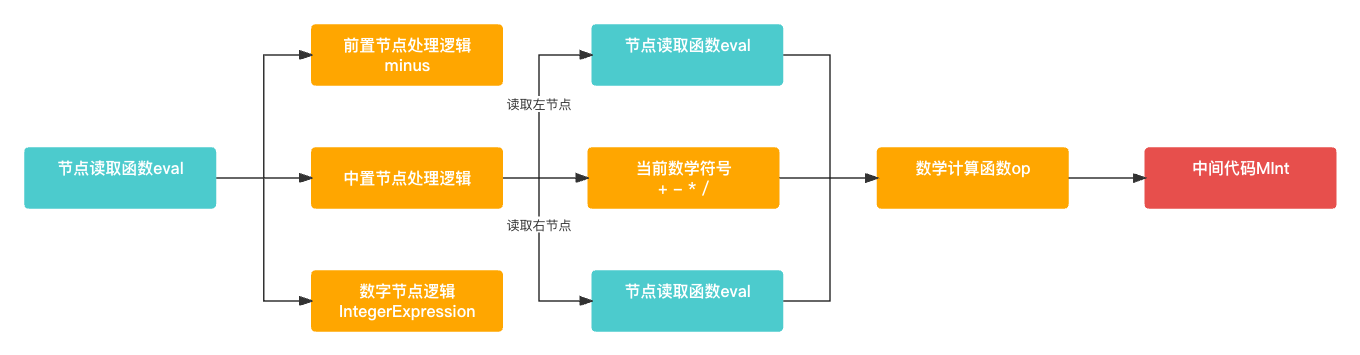
eval() 函数中主要有三个逻辑分支, 一个是数字的前置节点 一个是符号的前置节点, 最后一个是中置节点. 数字的前置节点 和 中置节点 没有什么好说的, 符号的前置节点 主要应对于第一个前置节点带符号的情况例如 -1 和 +349 等等.

public static func eval(_ node: Node?) -> MObj? {if let nodeValue = node as? IntegerExpression {// 纯数字节点逻辑return MInt(nodeValue.value)} else if let nodeValue = node as? PrefixExpression {// 带符号的数字节点逻辑if (nodeValue.operatorValue == "-") {return minus(node);} else if (nodeValue.operatorValue == "+") {return eval(nodeValue.right);}} else if let nodeValue = node as? InfixExpression {// 中置节点逻辑let left = eval(nodeValue.left);let right = eval(nodeValue.right);return op(left, right, nodeValue.operatorValue);}return nil;
}

op() 就是根据符号进行不同的数学运算, 整体逻辑比较简单, 这里就不过多叙述了.

public static func op(_ left: MObj?, _ right: MObj?, _ operatorValue: String?) -> MObj? {if let leftValue = left as? MInt,let rightValue = right as? MInt {switch(operatorValue) {case "+" :return MInt(leftValue.number + rightValue.number)case "-" :return MInt(leftValue.number - rightValue.number)case "*" :return MInt(leftValue.number * rightValue.number)case "/" :return MInt(leftValue.number / rightValue.number)case "^" :return MInt(pow(leftValue.number, rightValue.number))default:return nil;}}return nil;
}

minus() 函数主要是用来处理带符号的前置节点情况. 整体逻辑也比较简单, 这里就不过多叙述了.

public static func minus(_ node: Node?) -> MObj? {if let nodeValue = node as? PrefixExpression {let m : MObj? = eval(nodeValue.right);if let mValue = m as? MInt {if (nodeValue.operatorValue == "-") {mValue.number = -mValue.number}return mValue;}}return nil;
}

最后, 我们就能看到最终的输出结果.

var code = "1+2*3"var lexer: Lexer! = Lexer(code: code)var parser: Parser! = Parser(lexer)var expression: Expression? = parser.parseMain()if let intObj = Evaluator.eval(expression) as? MInt {print(intObj.toString())
}

总结

通过这篇博客详细大家对 PrattParser解析器的前端工作有个大体的了解了. 希望看这篇博客是可以一边断点项目, 一边查看, 主要是递归过程比较绕, 希望有耐心看完.