杭电oj--数列有序
有n(n<=100)个整数,已经按照从小到大顺序排列好,现在另外给一个整数x,请将该数插入到序列中,并使新的序列仍然有序。
输入数据包含多个测试实例,每组数据由两行组成,第一行是n和m,第二行是已经有序的n个数的数列。n和m同时为0标示输入数据的结束,本行不做处理。
对于每个测试实例,输出插入新的元素后的数列。
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner sc=new Scanner(System.in);while(sc.hasNext()){int n=sc.nextInt();//数组元素个数int m=sc.nextInt();//插入的元素if(n==0&&m==0) return;int[] arr=new int[n+1];for (int i = 0; i <n ; i++) {arr[i]=sc.nextInt();}for (int i = 0; i <n ; i++) {if(m<arr[i]){for (int j = n; j >i ; j--) {arr[j]=arr[j-1];}arr[i]=m;i=n;}}if(arr[n]==0) arr[n]=m;for (int i = 0; i <n ; i++) {System.out.print(arr[i]+" ");}System.out.println(arr[n]);}}
}相关文章:

杭电oj--数列有序
有n(n<100)个整数,已经按照从小到大顺序排列好,现在另外给一个整数x,请将该数插入到序列中,并使新的序列仍然有序。 输入数据包含多个测试实例,每组数据由两行组成,第一行是n和m,第二行是已…...
PHPEXCEL解决行数超过65536不显示问题
起因自然是导出数据到excel文件时,数据缺少现象。 百度讲解是将xls文件另存为xlsx文件。 除了这里的原因,还有一点是phpExcel存在两个写入类PHPExcel_Writer_Excel2007和PHPExcel_Writer_Excel5,而只有PHPExcel_Writer_Excel2007支持超过65…...

新媒体时代如何做好新型的网络口碑营销?
从人类开始交换商品的时代开始,口碑营销就已经存在,是靠口耳传播的营销方式。小马识途认为进入当今移动互联网时代,口碑营销又有了新的发展,网络口碑营销推广开始普及。营销人员将传统口碑营销与移动互联网营销相结合,…...
)
MySQL中InnoDB插入缓冲区(Insert Buffer)
一、插入缓冲区的基本原理 插入缓冲区(Insert Buffer,也称作 Change Buffer),是InnoDB存储引擎的一种内部机制,它允许系统将对非聚集索引页的写操作(例如插入、删除和更新)暂时缓存在内存中&am…...
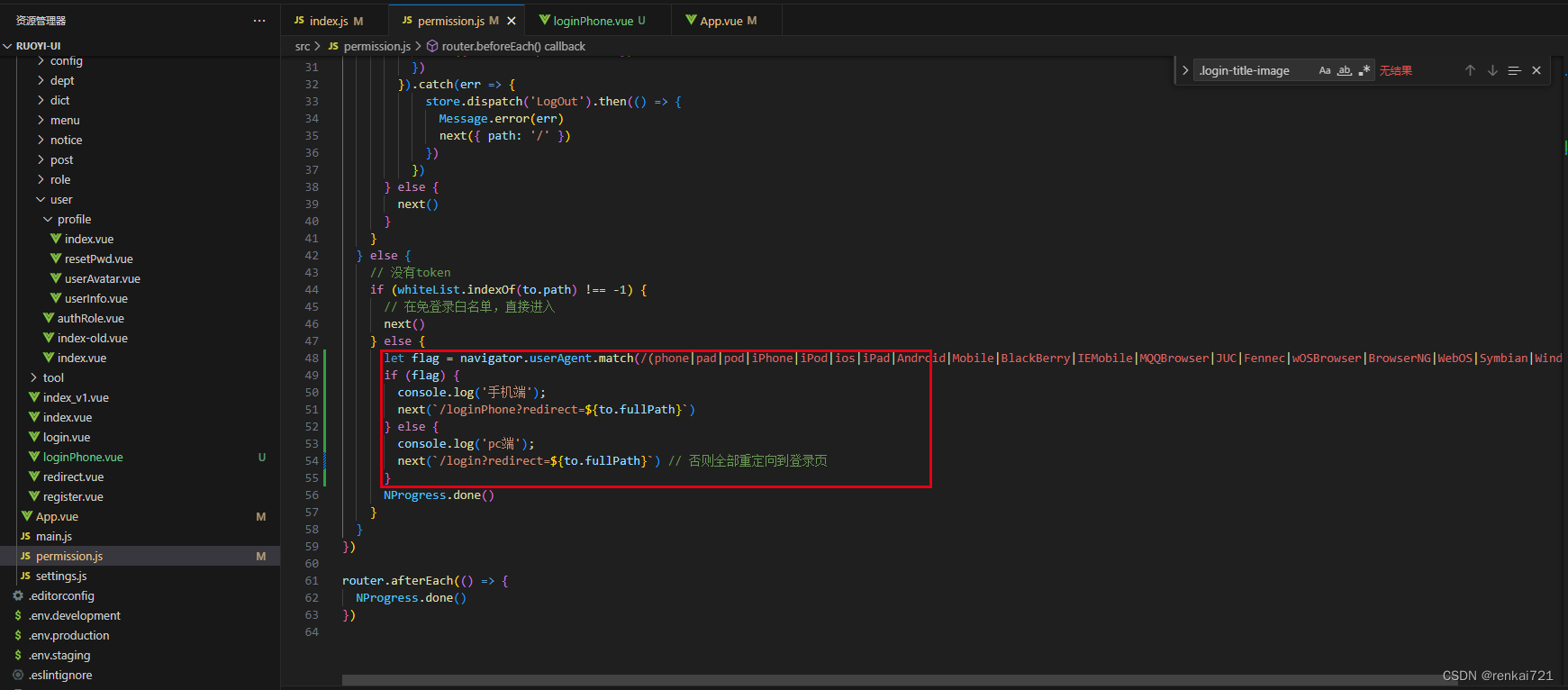
VUE前端判断是电脑端还是移动端
背景需求 ruoyi框架,前后端分离。现在要在用户访问的时候根据不同的设备跳转到不同的登录页面。 教程 router/index.js 修改src/router/index.js,在这里增加自己的要跳转的页面 permission.js 在白名单中添加自己的登录页面 增加以下识别的代码 le…...
OpenGL —— 2.8、漫游之摄像机飞行移动(附源码,glfw+glad)
源码效果 C源码 纹理图片 需下载stb_image.h这个解码图片的库,该库只有一个头文件。 具体代码: vertexShader.glsl #version 330 corelayout(location 0) in vec3 aPos; layout(location 1) in vec2 aUV;out vec2 outUV;uniform mat4 _modelMatrix; …...

AM@麦克劳林公式逼近以及误差分析
abstract 麦克劳林公式及其近似表示的应用误差估计和分析 Lagrange型泰勒公式的估计误差 由Lagrange型余项泰勒公式可知,多项式 p n ( x ) p_n(x) pn(x)近似表达函数 f ( x ) f(x) f(x)时,其误差为 ∣ R n ( x ) ∣ |R_{n}(x)| ∣Rn(x)∣ R n ( x ) R_{n}(x) Rn(x) f …...

gitlab 离线安装问题解决:NOKEY,signature check fail
1,rpm安装gitlab问题 test1:/opt # rpm -ivh gitlab-ce-16.0.3-ce.0.el7.x86_64.rpm --force warning: gitlab-ce-16.0.3-ce.0.el7.x86_64.rpm: Header V4 RSA/SHA1 Signature, key ID f27eab47: NOKEY error: [upel]: gitlab-ce NOKEY error: [upel]: gitlab-ce …...

uniapp使用uQRCode绘制二维码,下载到本地,调起微信扫一扫二维码核销
1.效果 2.在utils文件夹下创建uqrcode.js // uqrcode.js //--------------------------------------------------------------------- // github https://github.com/Sansnn/uQRCode //---------------------------------------------------------------------let uQRCode {…...

手写一个PrattParser基本运算解析器3: 基于Swift的PrattParser的项目概述
点击查看 基于Swift的PrattParser项目 PrattParser项目概述 前段时间一直想着手恶补 编译原理 的相关知识, 一开始打算直接读大学的 编译原理, 虽然内容丰富, 但是着实抽象难懂. 无意间看到B站的熊爷关于普拉特解析器相关内容, 感觉是一个非常好的切入点.所以就写了基于Swift版…...

三江学院“火焰杯”软件测试高校就业选拔赛颁奖仪式
11月25日下午,“火焰杯”软件测试开发选拔赛及三江-慧科卓越工程师班暑期编程能力训练营颁奖仪式在s楼会议室隆重举行。计算机科学与工程学院院长刘亚军、副院长叶传标、曹阳、吴德、院党总支副书记王兰英、系主任杨少雄、慧科企业代表尹沁伊人、项目负责人王旭出席…...

面试题-消息中间件篇-主流的消息中间件
消息中间件篇 第一章 主流的消息中间件对比 1、主流的消息中间件有 Kafka、RabbitMQ、ActiveMQ 等。 Kafka: Kafka 是一种高吞吐量、分布式、可扩展的发布/订阅消息系统,主要用于大数据处理和分析。Kafka 采用消息日志的方式来存储消息,可以…...

PyQt学习笔记-获取Hash值的小工具
目录 一、概述1.1 版本信息:1.2 基本信息:1.2.1 软件支持的内容:1.2.2 支持的编码格式 1.3 软件界面图 二、代码实现2.1 View2.2 Controller2.3 Model 三、测试示例 一、概述 本工具居于hashlibPyQtQFileDialog写的小工具,主要是…...

【(数据结构)— 双向链表的实现】
(数据结构)— 双向链表的实现 一.双向链表的结构二. 双向链表的实现2.1 头文件 ——双向链表的创建及功能函数的定义2.2 源文件 ——双向链表的功能函数的实现2.3 源文件 ——双向链表功能的测试2.4 双向链表各项功能测试运行展示2.4.1 双向链表的初始化…...
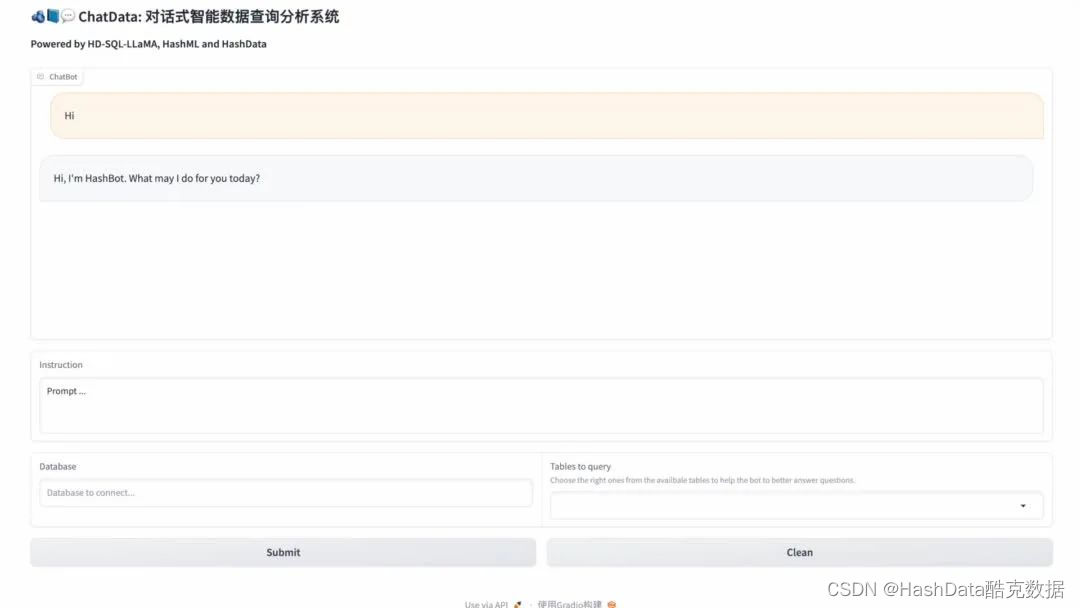
酷克数据发布HD-SQL-LLaMA模型,开启数据分析“人人可及”新时代
随着行业数字化进入深水区,企业的关注点正在不断从“数字”价值转向“数智”价值。然而,传统数据分析的操作门槛与时间成本成为了掣肘数据价值释放的阻力。常规的数据分析流程复杂冗长,需要数据库管理员设计数据模型,数据工程师进…...
FL Studio21最新中文破解进阶高级完整版安装下载教程
目前水果软件最版本是FL Studio21,它让你的计算机就像是全功能的录音室,大混音盘,非常先进的制作工具,让你的音乐突破想象力的限制。喜欢音乐制作的小伙伴千万不要错过这个功能强大,安装便捷的音乐软件哦!如…...

MDN--Web性能
CSS 动画与 JavaScript 动画 动画的实现可以有很多种方式,比如 CSS transition 和 animation 或者基于 JavaScript 的动画(使用 requestAnimationFrame()) CSS 过渡和动画 CSS transiton :创建当前样式与结束状态样式之间的动画。尽管一个元素处于过渡状态中&…...

Vue3.js:自定义组件 v-model
Vue3的自定义v-model和vue2稍有不同 文档 https://cn.vuejs.org/guide/components/v-model.html 目录 原生组件自定义组件CustomInput实现代码1CustomInput实现代码2 v-model 的参数 原生组件 <input v-model"searchText" />等价于 <input:value"s…...
)
AI虚拟主播开发实战(附源码)
人工智能 文章目录 人工智能前言 前言 https://blog.csdn.net/icemanyandy/article/details/124035967...

innoDB如何解决幻读
Mysql的事务隔离级别 Mysql 有四种事务隔离级别,这四种隔离级别代表当存在多个事务并发冲突时,可能出现的脏读、不可重复读、幻读的问题。其中 InnoDB 在 RR 的隔离级别下,解决了幻读的问题 事务隔离级别脏读不可重复读幻读未提交读ÿ…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
