JavaPTA练习题 7-4 计算给定两数之间的所有奇数之和
本题目要求接收输入的2个整数a和b,然后输出a~b之间的所有奇数之和。
输入格式:
分别用两行输入两个整数a,b
输出格式:
输出a~b之间的所有奇数之和
输入样例:
在这里给出一组输入。例如:
1
30
输出样例:
在这里给出相应的输出。例如:
SUM = 225---------------------------------------------------------------------------------------------------------------------------------
具体代码如下:
import java.util.Scanner;
public class Main{public static void main(String[] args){Scanner sc=new Scanner(System.in);int a=sc.nextInt();int b=sc.nextInt();int sum=0;while(a<=b){if(a%2!=0){sum+=a;a+=2;}else a++;}System.out.printf("SUM = "+sum);}
}
相关文章:

JavaPTA练习题 7-4 计算给定两数之间的所有奇数之和
本题目要求接收输入的2个整数a和b,然后输出a~b之间的所有奇数之和。 输入格式: 分别用两行输入两个整数a,b 输出格式: 输出a~b之间的所有奇数之和 输入样例: 在这里给出一组输入。例如: 1 30输出样例: 在这里给出相应的输出。例如: …...
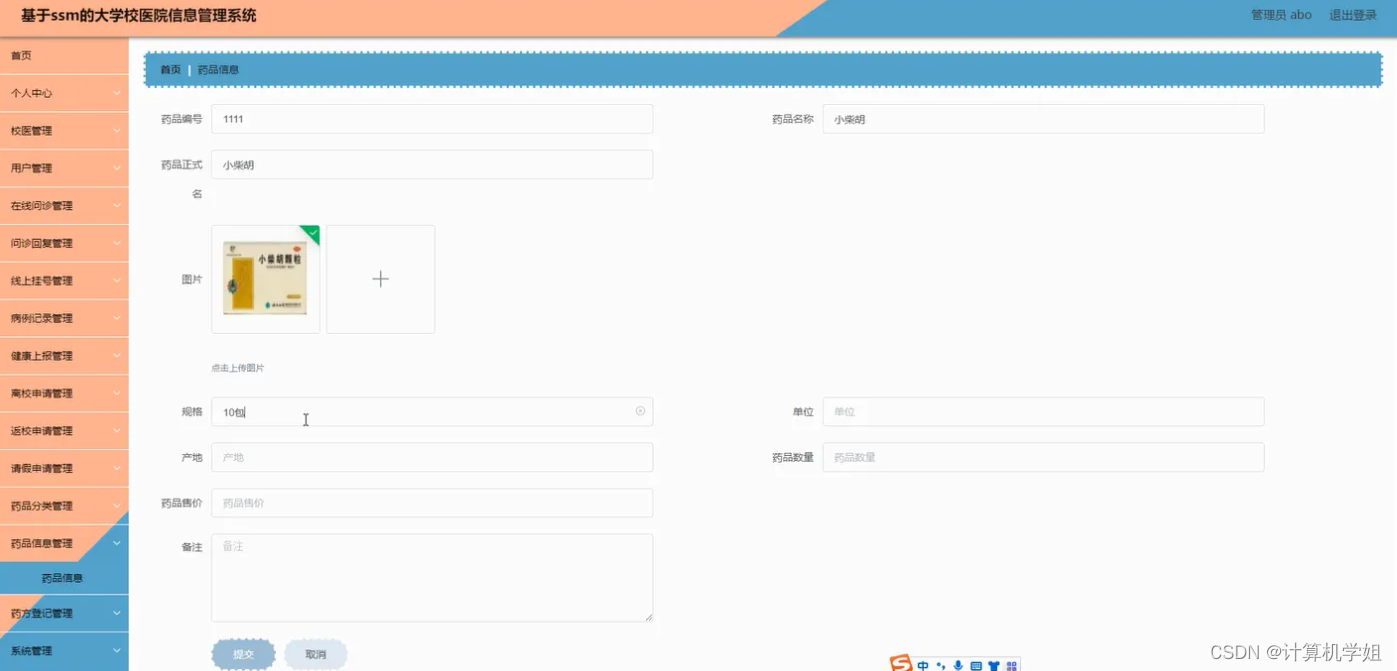
基于SSM的大学校医管理系统
基于SSM的大学校医管理系统、学校医院管理系统的设计与实现~ 开发语言:Java数据库:MySQL技术:SpringSpringMVCMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 主页 登录系统 用户界面 管理员界面 摘要 大学校医管理系统…...

【递归、搜索与回溯算法】第一节.初识递归、搜索与回溯算法
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:递归、搜索与回溯算法 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!&am…...

第十二届蓝桥杯模拟赛第一期
A填空题 问题描述 如果整数a是整数b的整数倍,则称b是a的约数。 请问,有多少个正整数是2020的约数。 答案提交 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数࿰…...

【生成对抗网络】
生成对抗网络(Generative Adversarial Networks,简称GANs)是深度学习领域的一种创新结构,由Ian Goodfellow在2014年首次提出。GANs包括两个深度神经网络——一个生成器和一个判别器,它们通常以对抗的方式进行训练。 以…...

Redis性能滑坡:哈希表碰撞的不速之客【redis第二部分】
Redis性能滑坡:哈希表碰撞的不速之客 前言第一部分:Redis哈希表简介第二部分:哈希表冲突原因第三部分:Redis哈希函数第四部分:哈希表冲突的性能影响第五部分:解决冲突策略第六部分:redis是如何解…...

科技与教育的盛宴——探讨监控易在82届教装展的新机遇
在第82届中国教育装备展示会这个融合了科技与教育的盛宴上,监控易将展现其最新的教育信息化解决方案和技术创新成果。这不仅是一次产品的展示,更是一次理念、技术与需求的交流和碰撞。在这里,我们将一同探讨在科技日新月异的今天,…...
Bazzite:专为 Steam Deck 和 PC 上的 Linux 游戏打造的发行版
导读对于一个专为 Linux 游戏定制的发行版,你是否感兴趣呢?如果答案是肯定的,那么我们为你准备了绝佳选择。 Bazzite 是一个新推出的基于 Fedora 的发行版,它是为 Linux 桌面上的游戏,以及越来越火热的 Steam Deck 定…...

【MySQL】数据库数据类型
文章目录 1. 整体概要2. 数值类型(有符号) tinyint 创建表(无符号) tinyint 创建表bit类型float 类型(无符号)floatdecimal 3. 二进制类型char类型varchar类型 4. 日期时间日期时间类型 5. string 类型enum类型和set类型enum类型和set类型的查找在枚举中的查找在set中的查找 1.…...

计算机组成原理 new07 真值和机器数 无符号整数 定点整数 定点小数 $\color{red}{Δ}$
文章目录 真值和机器数 无符号整数无符号整数的定义无符号整数的特征无符号整数的表示范围无符号整数的加法无符号数的减法 有符号整数(定点整数)有符号整数的定义原码原码的特点反码反码的特点补码补码的特点快速求解n位负数补码的方法为什么补码能够多表示一个范围(重点)变形…...
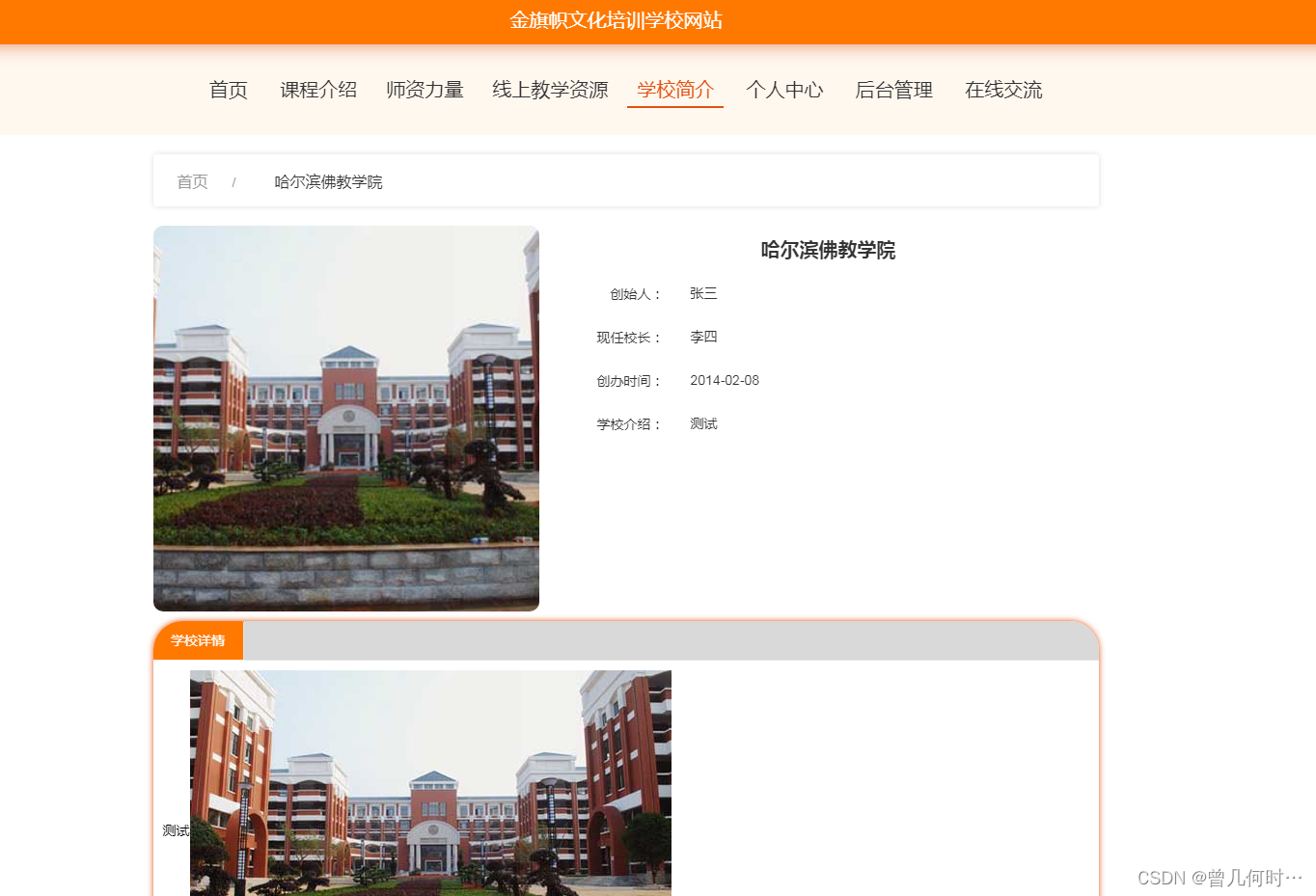
基于SSM的文化培训学校网站的设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

gitee-git使用
克隆gitee某代码仓库某分支流程 1.克隆远程gitee仓库某分支到本地 2.如果克隆gitee仓库是私有的系统会弹出弹框让你输入gitee的账户和密码 3.克隆远程分支完成 git所需命令 克隆远程仓库到本地 git clone 仓库URLgit克隆远程分支到本地 git clone -b 分支名 仓库URLgit 拉…...
)
欧拉图(Euler Graph)
这种「一笔画」问题与欧拉图或者半欧拉图有着紧密的联系,下面给出定义: 通过图中所有边恰好一次且行遍所有顶点的通路称为 欧拉通路; 通过图中所有边恰好一次且行遍所有顶点的回路称为 欧拉回路; 具有欧拉回路的无向图称为 欧拉图; 具有欧拉通路但不具有欧拉回路的无向图…...

【安全体系架构】——零信任网络架构
什么是零信任网络架构? 零信任网络架构是一种网络和信息安全模型,它将传统的信任模型颠覆,不再信任内部或外部用户、设备或网络。相反,它将每个访问请求都视为不受信任,要求对每个用户、设备和流量都进行认证和授权&a…...

mybatis动态sql一对多查询
在数据库设计中,一对多关系是非常多的,例如消息通知和附件,一个消息通知中往往会包含多个附件,这种情况下使用mybatis动态sql可以很方便的查询出来。 1、数据库设计 消息表:sys_message CREATE TABLE sys_message (i…...
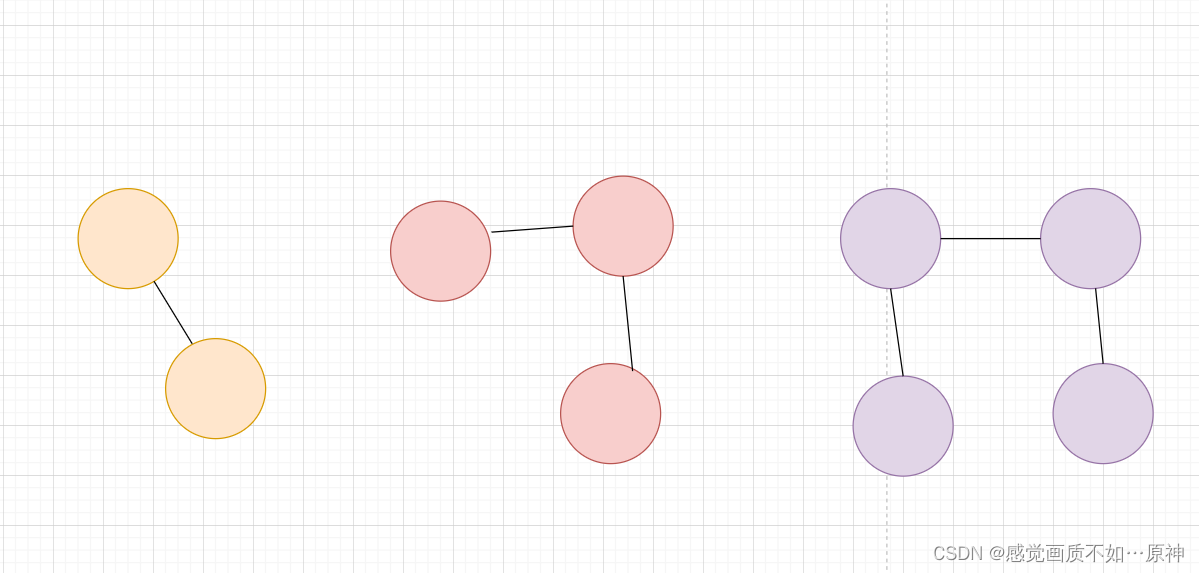
Leetcode.2316 统计无向图中无法互相到达点对数
题目链接 Leetcode.2316 统计无向图中无法互相到达点对数 rating : 1604 题目描述 给你一个整数 n n n ,表示一张 无向图 中有 n n n 个节点,编号为 0 0 0 到 n − 1 n - 1 n−1 。同时给你一个二维整数数组 e d g e s edges edges ,其…...

介绍机器学习中CatBoost工具的详细使用指南
在机器学习的动态世界中,Python 是创新背后的驱动力,专业人士必须使用正确的工具。CatBoost 就是这样一个工具,以其卓越的速度和准确性悄然改变了该领域。在本指南中,我们将深入研究 Python 3 中的 CatBoost,涵盖基础知识、高级技术和实际示例,包括使用示例数据集和绘图进…...

操作系统【OS】线程与进程的比较
进程 线程 是什么的单位? 是资源分配的基本单位 是调度的基本单位 不能共享什么? 不能共享虚拟地址空间 不能共享栈指针 可以共享什么? 拥有一个完整的资源平台 每个进程都有独立的地址空间和资源 除了共享全局变量,不允许其他进程访问 某进程中的线程…...
在Mac上使用安卓桌面模式
在安装Homeblew的基础上 替换国内源 export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" export HOMEBREW_BREW_GIT_REMOTE"https://mirrors.tuna.tsinghua.edu.cn/git/homebrew/brew.git" brew update 安装Scrcpy …...

YOLO目标检测——人脸口罩佩戴数据集【(含对应voc、coco和yolo三种格式标签】
实际项目应用:公共场所监控场景下的大密度人群检测是否佩戴口罩,以及戴口罩的人证比对(安检刷脸不用摘口罩)、手机解锁、刷脸考勤等身份认证场景。数据集说明:人脸口罩佩戴检测数据集,真实场景的高质量图片…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...
