含分布式电源的配电网日前两阶段优化调度模型(Matlab代码实现)
👨🎓个人主页:研学社的博客
💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 文献来源
🌈4 Matlab代码、数据、文章讲解
💥1 概述
文献来源:


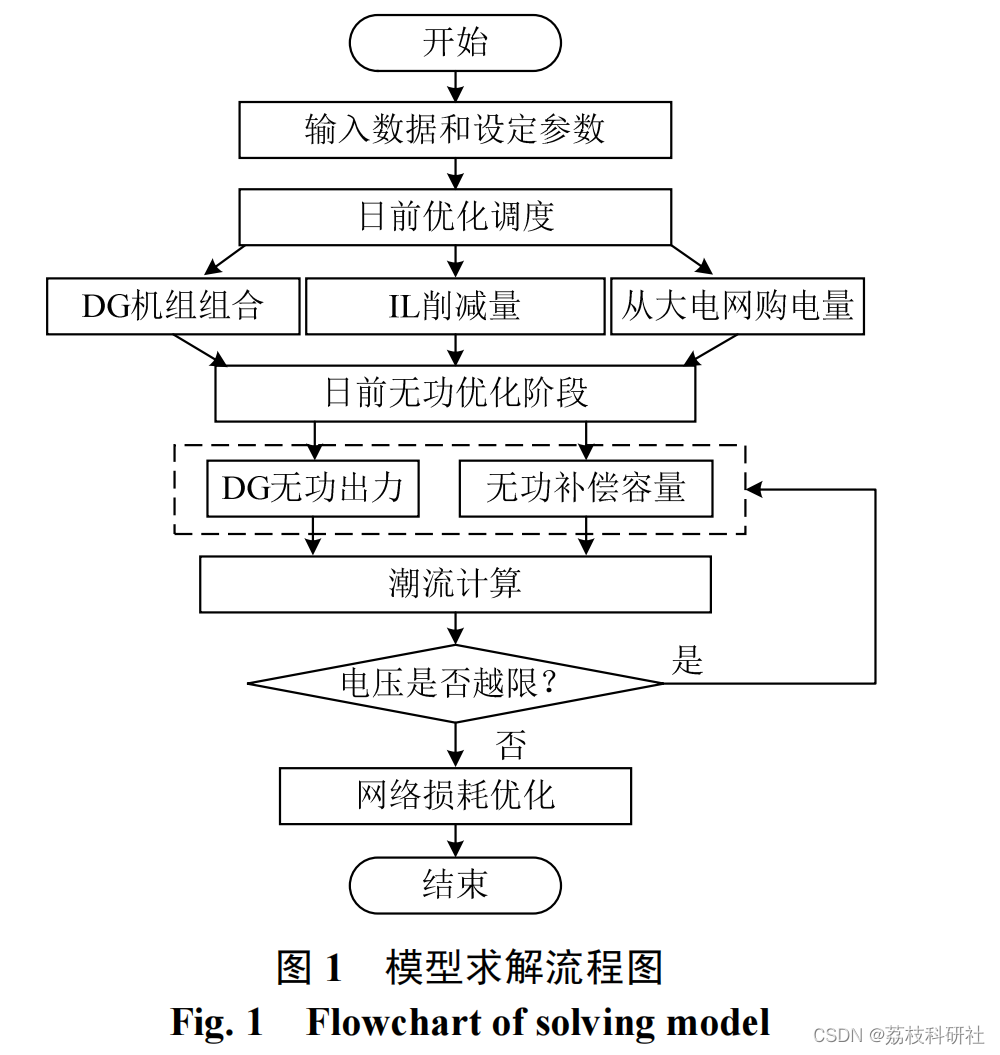
摘要:在电力市场环境下,供电公司通过对接入配电网的分布式电源(distributed generation,DG)的优化调度,能够有效地降低其运行成本,规避市场竞争环境下的风险。提出了一种电力市场环境下供电公司日前优化调度的2阶段模型:第1阶段为DG优化调度阶段,根据市场电价、DG运行成本、签订可中断负荷(interruptable load,IL)合同的价格来确定DG的机组组合、从大电网的购电量及IL削减量;第2阶段为无功优化阶段,在第1阶段的基础上,考虑DG的无功出力特性,通过优化DG和无功补偿装置的出力调节电压使其在规定的范围内且配电网的网损最小。通过基于修改的IEEE 33节点系统的仿真计算,表明所提出的日前2阶段优化调度模型能够有效降低供电公司的运行成本。
关键词:
电力市场;分布式电源;机组组合;可中断负荷;无功补偿;配电网;
在输电和配电相分离的电力市场环境下,供电公司面临着各种不确定性问题,尤其是实时电价波
动所带来的风险。随着分布式电源(distributed generation,DG)在配电网中渗透率的提高,供电公
司在参与电力市场的同时开始优化 DG 的调度运行来降低经济风险[1]。在各种 DG 中,风电、光伏的出力具有随机性与波动性,可调度性差,而燃气轮机、燃料电池、柴油机等 DG 的输出可以自由调节,可调度性好。可中断负荷(interruptable load,IL)是需求侧管理的一种重要手段,在电网高峰时段由供电公司向用户发出中断指令,经用户响应后中断部分用电。在电力市场环境下,供电公司对 DG 和 IL进行优化调度后,可以有效节约配电网的运行成本,提高系统运行的安全可靠性。
目前国内对于含 DG 配电网的研究主要集中在DG 接入后对配电网供电质量、电压分布、电压稳
定、可靠性、继电保护的影响等方面[2-4],以及配电网中分布式电源的规划问题[5-7]上。而国外已开展了电力市场环境下含分布式电源的配电网经济调度问题研究,文献[8]提出了有源配电网的日前和日内2 阶段运行模型,日前主要是 DG 调度,日内是对负荷和机组出力做出校正;文献[9]在前者的基础上考虑了二氧化碳排放的问题,并作为惩罚项加入目标函数;文献[10]在分布式电源高渗透率的情况下提出了配电网的短期调度和控制模型,文献[11-12]研究了为了降低用电成本,在需求响应机制下制定日前用电计划的优化方法,文献[13-15]分别从用电成本最低、电力公司运行成本最低和多目标优化角度研究了一组用户联合制定用电计划的方法。

📚2 运行结果
本文采用修改后的 IEEE 33 节点配电系统来验证所提出的日前调度模型的有效性。假设 3 个可调
DG(本文采用柴油发电机)分别连接在 7、24、25 号节点上,风机和光伏分别接在 14 和 31 节点上,IL用户接在 8、25 号节点上,3 个无功补偿装置分别接在 8、30、32 号节点上,如图 2 所示。
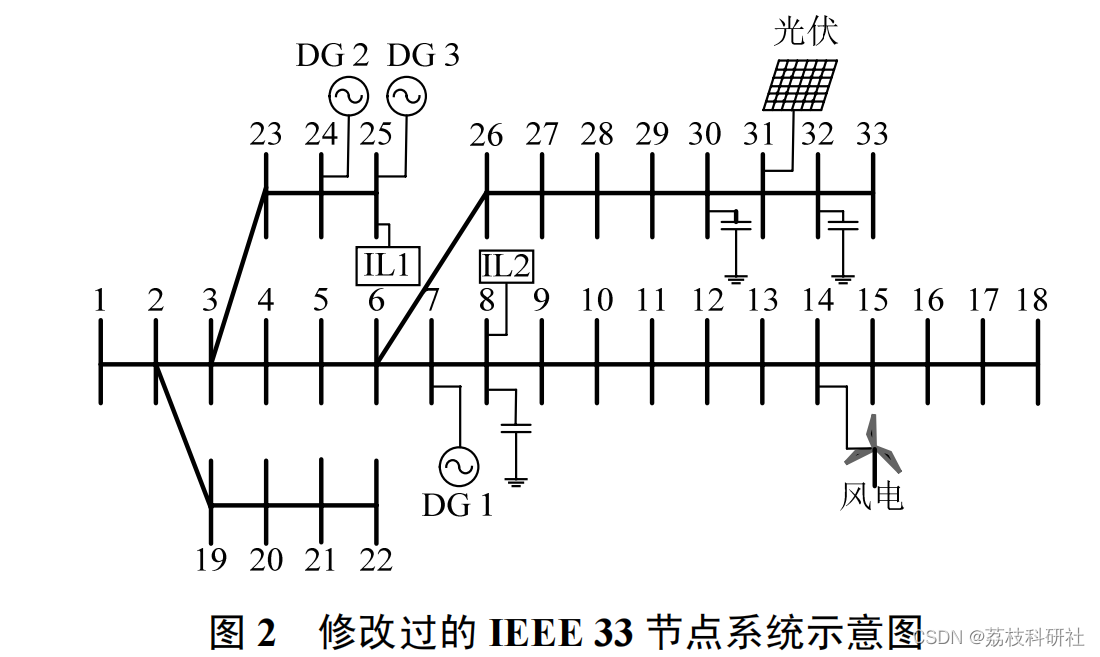

原文图:
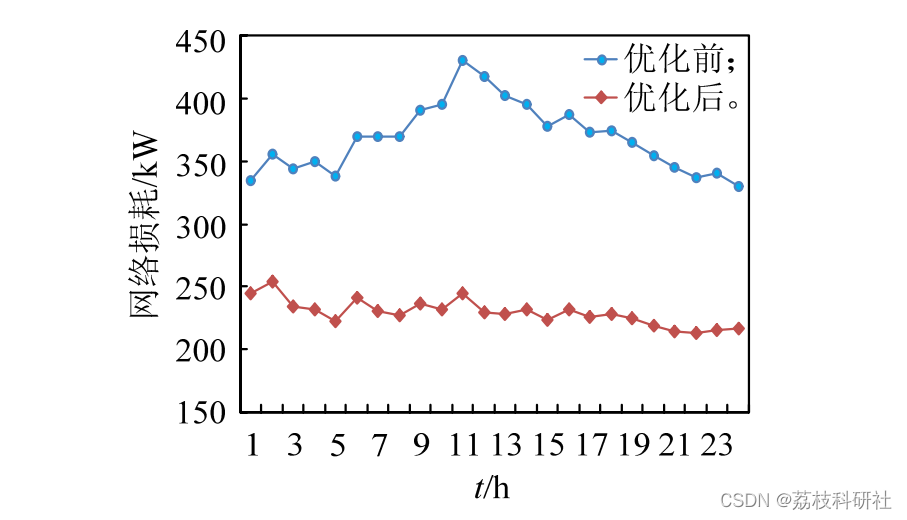

复现图:
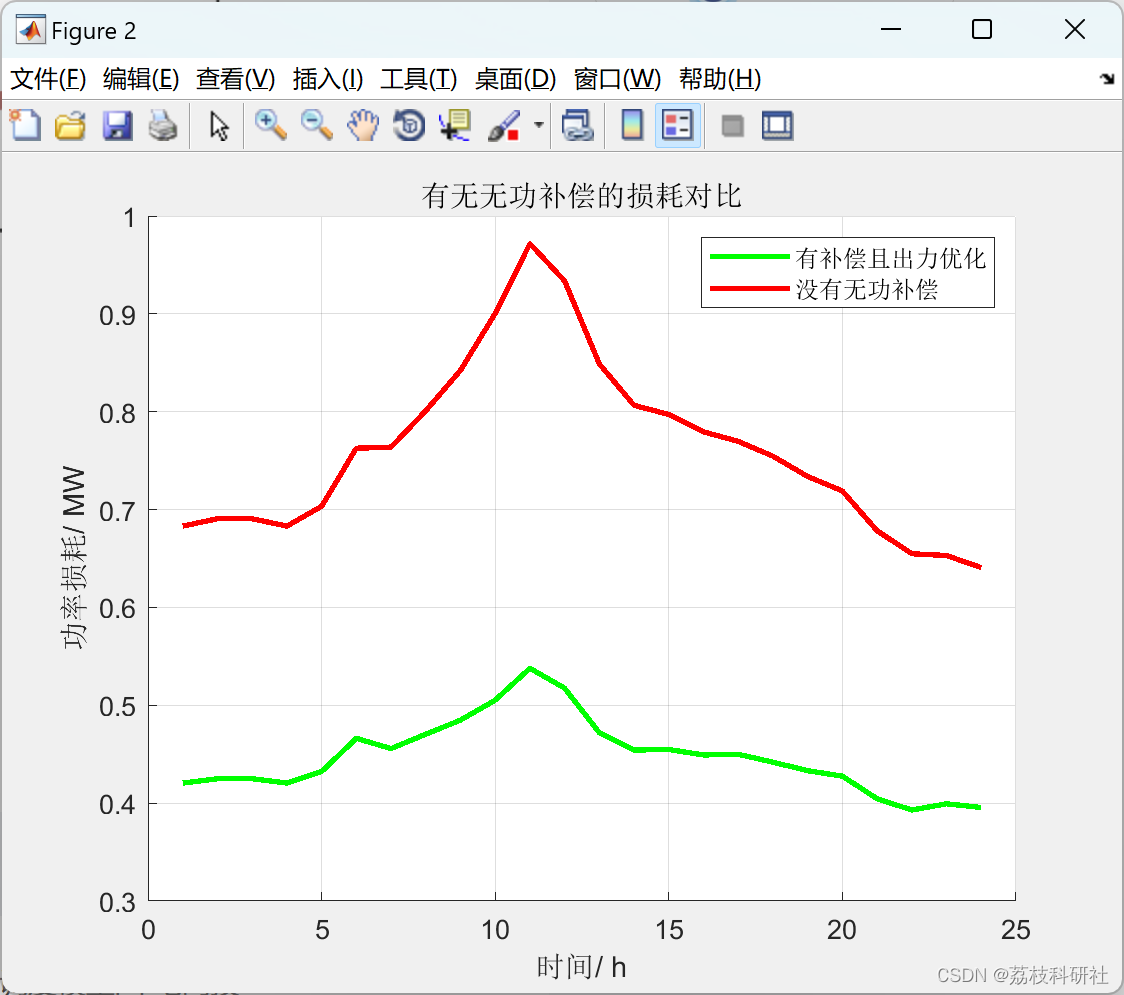

🎉3 文献来源
部分理论来源于网络,如有侵权请联系删除。
[1]孟晓丽,高君,盛万兴等.含分布式电源的配电网日前两阶段优化调度模型[J].电网技术,2015,39(05):1294-1300.DOI:10.13335/j.1000-3673.pst.2015.05.019.
🌈4 Matlab代码、数据、文章讲解
相关文章:

含分布式电源的配电网日前两阶段优化调度模型(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...
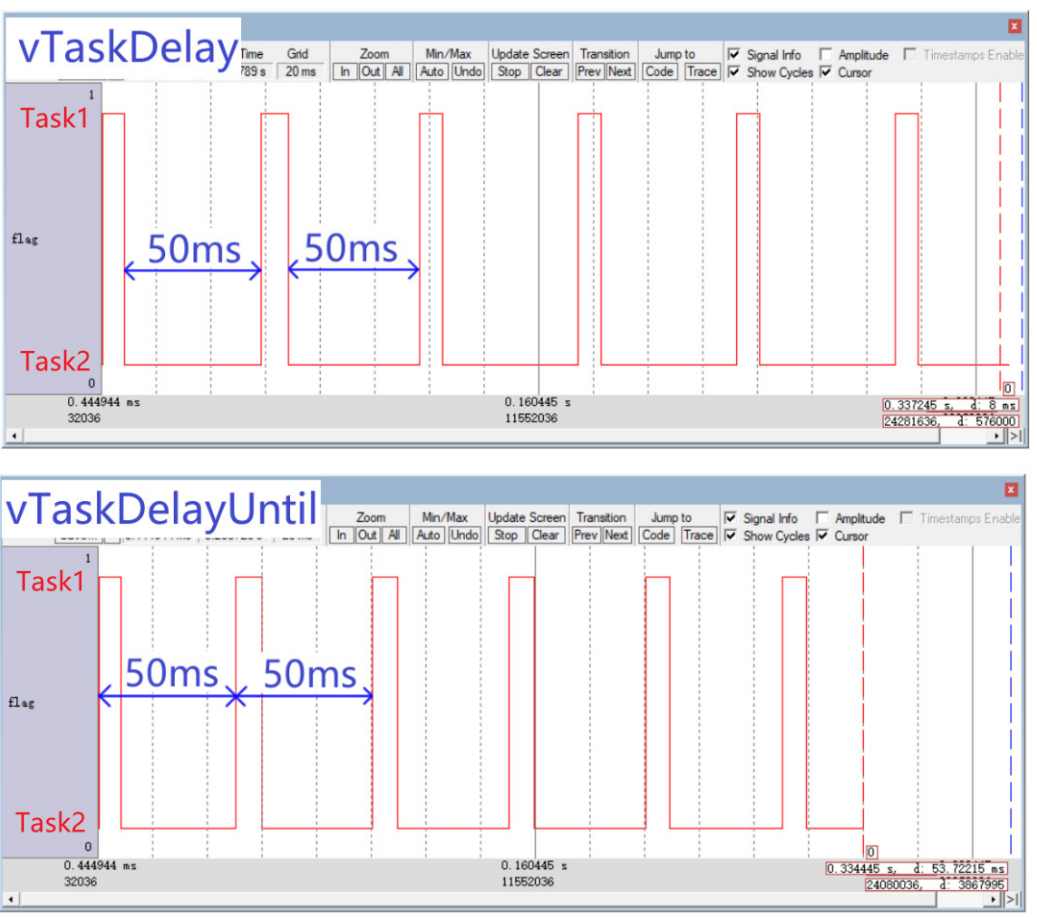
FreeRTOS的Delay函数
两个Delay函数有两个延时函数vTaskDelay:至少等待指定个数的Tick Interrupt才能变为就绪态xTaskDelayUtil:等待到指定的绝对时刻,才能变为就绪态个人感觉这两个延时函数就是,比如一个我等3个小时,一个是我等到下午3点的…...
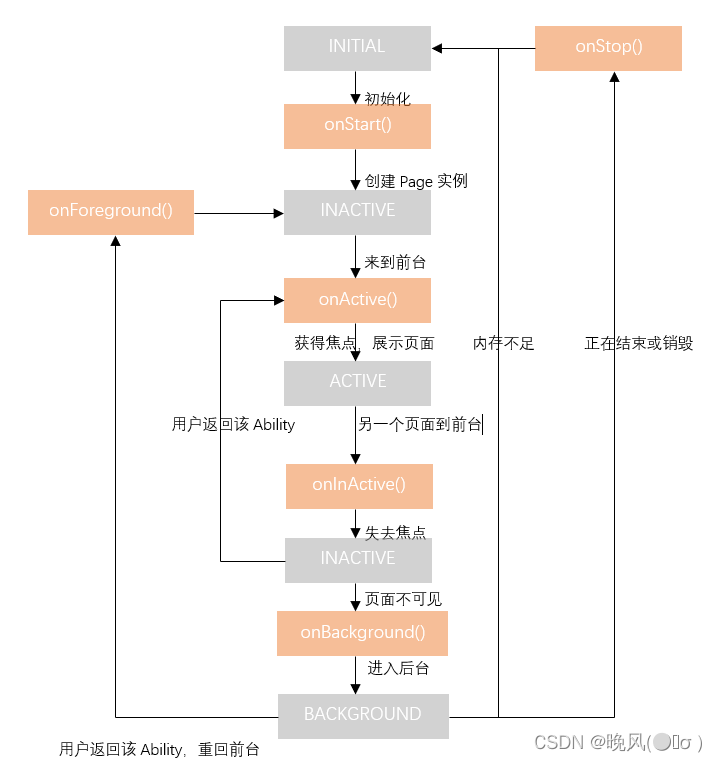
HCIA-HarmonyOS Application Developer——题目集1
题目1 1、一位开发人员在设计应用程序时,添加了一个Text组件和Button组件,开发样图如下所示。该开发者不能选择哪种布局方式来放置组件? A、StackLayout B、DependentLayout C、DirectionalLayout D、TableLayout 解析:(A&#…...

高性能 Message ToJavaBean 工具 【easy.server.mapper】
easy.server.mapper 介绍 后端开发中,消息转换常见问题 Map 中的数据 转换成实体Bean数组 中的数据 转换成实体BeanServet 中的 param 转换成实体Bean 以上的三个问题是最常见的消息转换困扰。 以Map 举例 常见做法是 手动转换 Map<String,Object> da…...
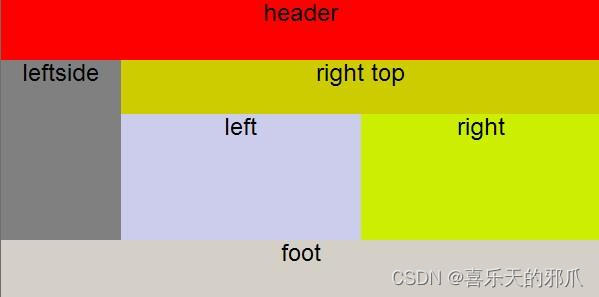
Web前端学习:三 - 练习
三六:风筝效果 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title><style type"text/css">*{margin: 0;padding: 0;}.d1{width: 200px;height: 200px;background: yellow;position…...

面试题:Android 中 Intent 采用了什么设计模式?
答案是采用了原型模式。原型模式的好处在于方便地拷贝某个实例的属性进行使用、又不会对原实例造成影响,其逻辑在于对 Cloneable 接口的实现。 话不多说看下 Intent 的关键源码: // frameworks/base/core/java/android/content/Intent.java public cla…...

Java数据类型与变量
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【JavaSE_primary】 文章目录字面常量数据类型变量整型变量字节型变量浮点数变量双精度浮点数单精度浮点数字符型变量布尔型变量空常量nu…...

Python为CANoe工程添加/删除DBC文件
前面文章我们对于通过COM来实现打开CANoe、导入CANoe配置工程、导入执行文件、启动CANoe软件和执行脚本;但是这只能完成最基本的功能调用,在实际得到使用过程中,特别是各家在推的CI/CD以及平台化,仅仅是实现这些功能是完全不够用的;比如dbc的添加和删除,这是我们非常必要…...

不同的产品经理特征和需要的能力
产品经理是一个管家,需要和各方沟通推动产品各个决策进展。 每天早上看看线上用户数据、看下今天要安排任务,接着就是和各方开会讨论推动产品实现。每天穿插于与 UI、用户以及完成自己的 todolist 中循环。如果公司体制完善,还要和运营、数据…...

webpack之处理样式资源
处理样式资源 本章节我们学习使用 Webpack 如何处理 Css、Less、Sass、Scss、Styl 样式资源 #介绍 Webpack 本身是不能识别样式资源的,所以我们需要借助 Loader 来帮助 Webpack 解析样式资源 我们找 Loader 都应该去官方文档中找到对应的 Loader,然后…...

Golang 接口笔记
基本介绍接口是一个数据类型,可以定义一组方法,但都不需要实现。并且interface中不能包含任何变量。到某个自定义类型要使用的时候,再根据具体情况把这些方法实现出来语法type 接口名 interface {method1(参数列表) 返回值列表method2(参数列…...
[计算机网络(第八版)]第二章 物理层(章节测试/章节作业)
章节作业 带答案版 选择题 (单选题)双绞线是用两根绝缘导线绞合而成的,绞合的目的是( )。 A. 减少干扰 B. 提高传输速度 C. 增大传输距离 D. 增大抗拉强度(单选题)在电缆中采用屏蔽技术可以带来的好处主要是( )。 A…...
 类)
[iOS 理解] Swift Runtime (1) 类
Warm up 先看一段代码: import ObjectiveCclass Obj {var x: Double 0 }let v: NSObjectProtocol Obj() as! NSObjectProtocol let result v.isKind(of: Obj.self) let size class_getInstanceSize(Obj.self)我们有一个没有继承 NSObject、没有遵循 NSObjectP…...
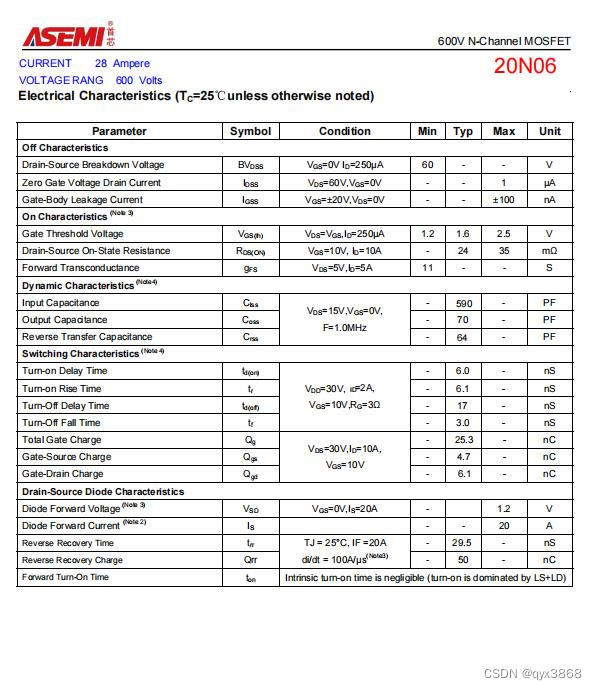
ASEMI低压MOS管20N06参数,20N06体积,20N06大小
编辑-Z ASEMI低压MOS管20N06参数: 型号:20N06 漏极-源极电压(VDS):60V 栅源电压(VGS):20V 漏极电流(ID):20A 功耗(PD࿰…...
(四))
常见前端基础面试题(HTML,CSS,JS)(四)
作用域和作用域链的理解 作用域 (1)全局作用域 最外层函数和最外层函数外面定义的变量拥有全局作用域所有未定义直接赋值的变量自动声明为全局作用域所有window对象的属性拥有全局作用域全局作用域有很大的弊端,过多的全局作用域变量会污染…...

RabbitMQ发布确认模式
目录 一、发布确认原理 二、发布确认的策略 (一)开启发布确认的方法 (二)单个确认模式 (三)批量确认模式 (四)异步确认模式 (五)如何处理异步未确认消…...

零基础的人如何入门 Python ?看完这篇文章你就懂了
第一部分:编程环境准备 零基础入门Python的话我不建议用IDE,IDE叫集成开发环境,这东西一般是专业程序员用来实战开发用的,好处很多,比如:调试、语法高亮、项目管理、代码跳转、智能提示、自动完成、单元测…...

Atcoder abc257 E
E - Addition and Multiplication 2 题意: 给你一个数字n表示你现在拥有的金额 然后给你1~9每个经营额所需要的成本, 设总经营额为x, 当前使用的经营额为y, 则每一次使用经营额时都有x10*xy 问, 如何在使用不大于成本数量的金额下, 使得经营额最高 例如: 5 5 4 3 8 1 6 7 …...

模拟退火算法改进
import numpy as np import matplotlib.pyplot as plt import math import random from scipy.stats import norm from mpl_toolkits.mplot3d import Axes3D # 目标函数 def Function(x, y): return -20 * np.exp(-0.2*np.sqrt(0.5*(x*xy*y)))\ -np.exp(0.5*(n…...
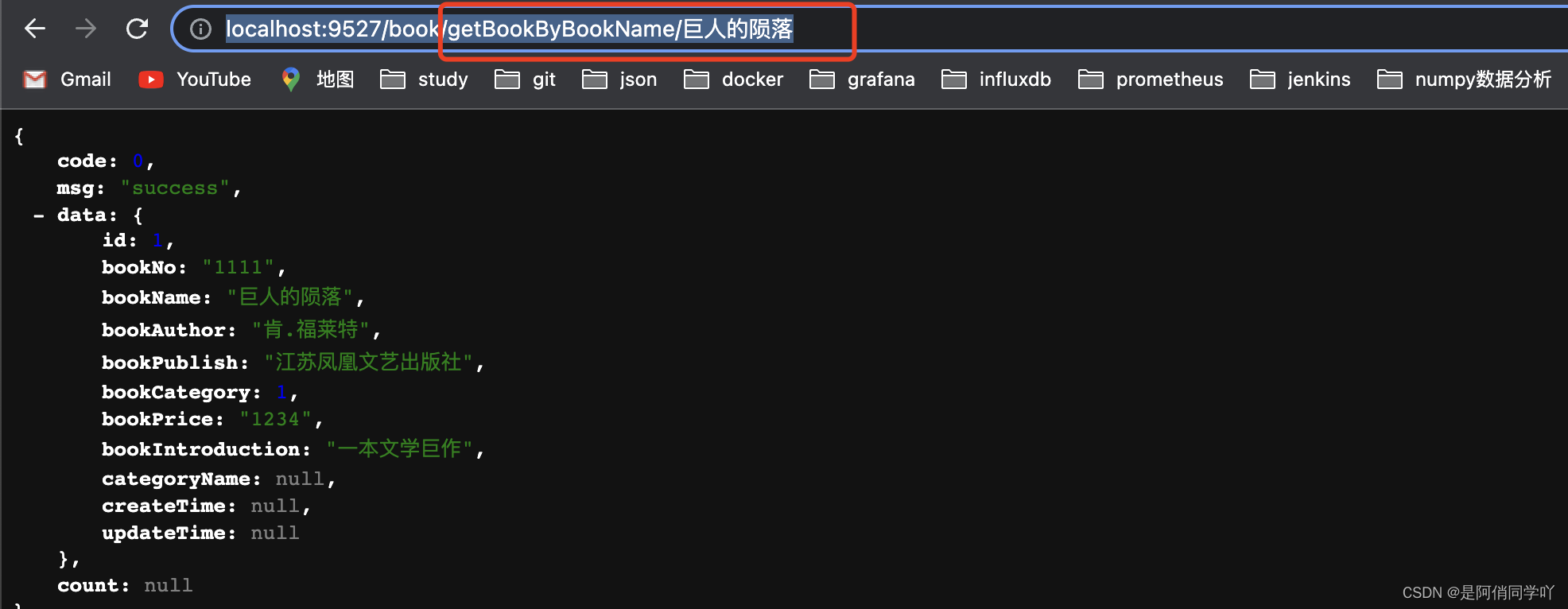
SpringBoot+HttpClient+JsonPath提取A接口返回值作为参数调用B接口
前言 在做java接口自动化中,我们常常需要依赖多个接口,A接口依赖B,C,D接口的响应作为请求参数;或者URL中的参数是从其他接口中提取返回值作获取参数这是必不可少的。那么怎么实现呢?下面就来介绍多业务依赖…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
