线性代数1:线性方程和系统

图片来自施泰德博物馆
一、前言
通过这些文章,我希望巩固我对这些基本概念的理解,同时如果可能的话,通过我希望成为一种基于直觉的数学学习方法为其他人提供额外的清晰度。如果有任何错误或机会需要我进一步阐述,请分享,我可以进行必要的修改。
这是关于线性代数基础知识的持续系列文章的第一个补充,线性代数是机器学习背后的基础数学。本文最好与David C. Lay,Steven R. Lay和Judi J. McDonald的线性代数及其应用一起阅读。将此系列视为外部配套资源。
二、背景
线性方程组和线性方程组在金融、工程、化学、计算机科学、统计学和物理学等领域具有各种实际应用。在化学中,线性方程用于平衡化学反应并计算反应物和产物的数量。线性代数的这一基石也出现在物理学中,其中线性方程在运动学和热力学中使用来描述物体的运动,帮助计算距离、速度和加速度,并分别模拟物理系统中的传热和能量流。金融领域依靠线性方程和系统进行预算和投资组合分析,而工程师可以使用相同的工具进行结构分析,以模拟建筑物中的力和应力。线性代数无处不在;每个人都可以在某种程度上欣赏它。
三、线性方程
线性方程是具有一个或多个变量的方程,对于每个变量,变量的指数必须为 2。它可以写成以下形式:a₁x₁ + a₂x₂ + ... + <>rxr = b。值 [a₁, a₁, ..., ar] 和 b 称为线性方程的系数。
线性方程的示例包括:2 x + 5 y = 10、6 x = 18、7v + 8w + 0 x + 2y + 3z = 15,以及 3 x₁ + 4x₂ + 5x₃+9x₄ + 10x₇ = 3。
线性方程的非示例是 2x² + 6x + 5 = 2;这是二次方程*的一个实例。另一个这样的非示例可能是 7x₁ + 3 x₂ = x₁* y₁; 当你绘制这个方程时,其原因变得很明显,它可以重新排列以形成有理函数 y = 7 x /x - 3,它是弯曲 的而不是线性的。
考虑线性方程 2x + 5y = 10。下图说明了线性方程的图形表示,您会注意到它是一条线。当调用直线的方程时,这一点变得更加明显:y = mx + b,其中 m = 斜率和 b = y 截距。线性方程可以如下图所示重新排列以采用这种形式。
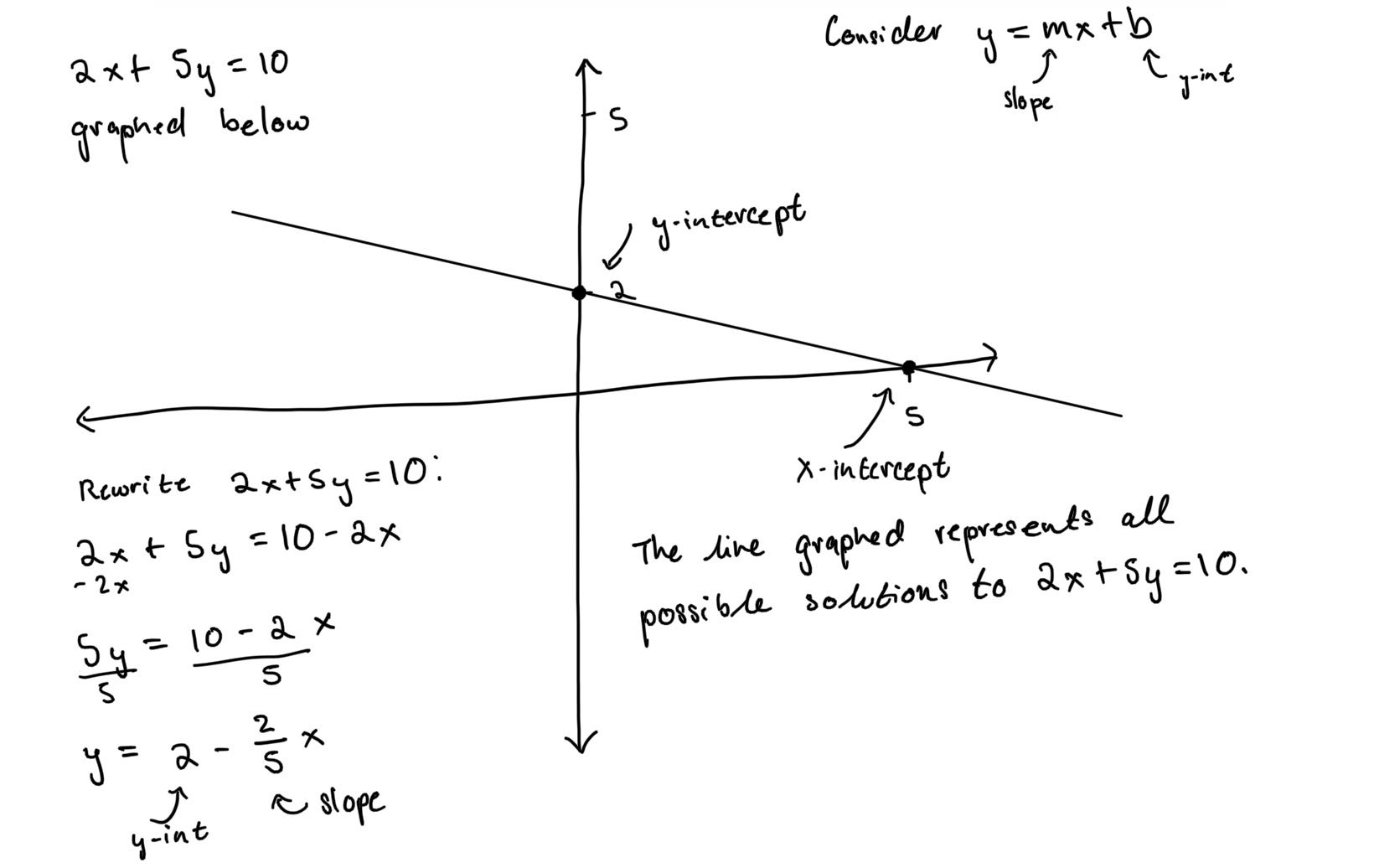
可以得出以下结论:落在直线上的所有 (x, y) 点都是方程 2x + 5y = 10 的解。例如,假设我们选择 x 截距的点 (5, 0),并将 x 和 y 值代入方程中各自的位置。2(5) + 5(0) = 10。线上的任何 (x, y) 点都可以代入方程中,并且相等性将成立。我们可以将这一发现概括为一个规则:
具有两个变量 ax + by = c 的线性方程的 R²* 中的解集可以表示为一条线。
请注意,这个奇异方程有无限数量的解,跨越 R²;稍后我们将仔细研究解决方案的数量。
相同的基本概念转移到表示为 Rⁿ 的高维坐标空间,例如 R³,其中由于添加了第三个变量,直线成为平面。
四、线性方程组
线性方程组是一个或多个线性方程的集合,这些方程共享相似的变量。举个例子:
6x + 2y = 4
2x + 4y = 8
线性方程组的解定义为值(s₁,s₂,...,sr),当替换每个方程各自的变量时,这些值使每个方程为真。在上述系统的情况下,解将是(0,2),因为当(0,2)被替换到系统中时,两个方程的计算结果都是真的。
五、线性系统的解决方案
线性系统解的图形含义是什么?线性系统的解决方案数有哪些不同情况?本节将更详细地研究三种可能性中的每一种。它们如下:
- 独特的解决方案
- 没有解决方案
- 无限解决方案
唯一解决方案:对于具有两个变量(如上述变量)的线性系统,解决方案是交叉点。为什么?解是有序对,其中两个方程都必须满足,如果不存在这样的有序对,那一定意味着直线永远不会相交。这是一个独特解决方案的示例。只有一个解可以满足线性系统中的所有方程。
没有解决方案:考虑没有解决方案的情况。在具有两个变量的线性系统的上下文中,这可能意味着什么?在什么情况下,一组行永远不会相遇?一种情况是,如果它们是平行的。对于所有直线都平行的线性系统,线性系统将没有解。另一种情况是,虽然某些线可能与其他线相交,但没有一条所有线共享的共同交点。
无限解:线性系统的最终情况是存在无限解。什么时候有可能为双变量线性系统提供无限解?如果线相同,则存在无限的交点,因为它们重叠,因此存在无限解。考虑以下线性系统:
6x + 3y = 18
2x + y = 6
虽然系数可能不同,但这些线实际上是相同的!如果将第一个方程的每个系数除以 3,则得到的方程将为 2x + y = 6。
线性系统解数的可视化随着变量数量的增加而变化。下图是具有三个变量的线性系统的所有三个解案例的可能图。三维之后的任何东西都变得难以想象,但同样的规则适用!无论有多少变量,所有线性系统要么没有解,要么只有一个解,要么有无限解。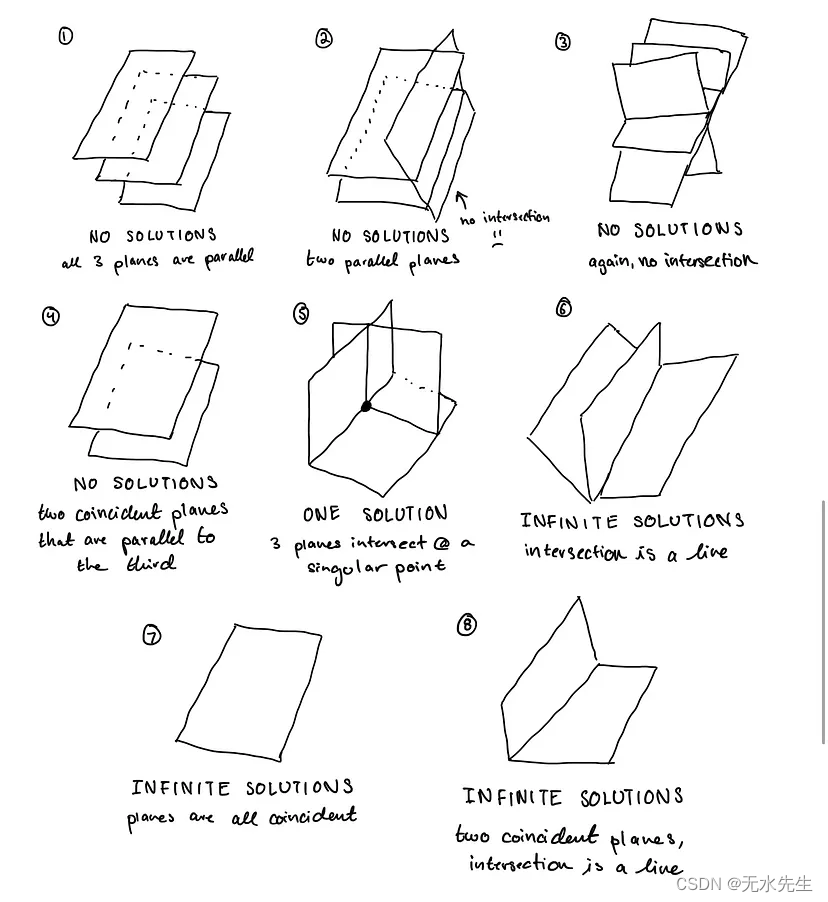
此图改编自 src。
六、矩阵表示法
随着线性方程变得越来越复杂,符号可能会变得笨拙。将线性系统的信息压缩为易于操作和使用非常重要,因此矩阵符号通常用于一组方程。系数矩阵是一种从每个方程中排除 b 系数的矩阵。增强矩阵包含 b 系数,因此它比系数矩阵多一列。

矩阵的大小(也称为顺序)告诉我们矩阵有多少行和列。m x n 矩阵是包含 m 行和 n 列的矩阵。行数对应于系统有多少个线性方程,而列数告诉我们有多少变量。注意确保行数在列数之前,因为顺序不可互换。
七、求解线性系统
有一种系统的方法可以确定线性系统是否有解,如果有,它是否有唯一的解或无限解,并从那里获得解。求解线性系统可以使用原始形式的线性方程或矩阵来执行,但建议使用矩阵,因为符号更清晰、更紧凑。然而,熟悉这两种方法是件好事,因为它们提供了对另一种方法机制的额外见解。
下面是解决无矩阵方程组的逐步过程。基本思想是通过将预先存在的方程相乘来创建新方程,以获得相同的方程,然后可以从另一个方程中添加或减去以消除一个变量。然后重复这个过程,直到我们从系统中消除了足够多的未知数,以便能够解决一个变量,然后通过反向替换来求解其余变量。最后,需要进行检查以确保解实际上满足方程组。

八、行操作
前面概述的步骤可以转移到以矩阵为中心的求解线性系统的过程。记下每次转换后如何在矩阵中指定消除的变量。但是,在我们开始之前,让我们定义一些行操作。两个实际上与我们之前应用的操作并行。
- 替换:“将一行替换为其自身和另一行的总和。*
- 交换:“交换两行。*
- 缩放:“将一行中的所有条目乘以非零常量。*
让我们再次重新接近相同的线性系统,但这次使用矩阵并应用行运算。
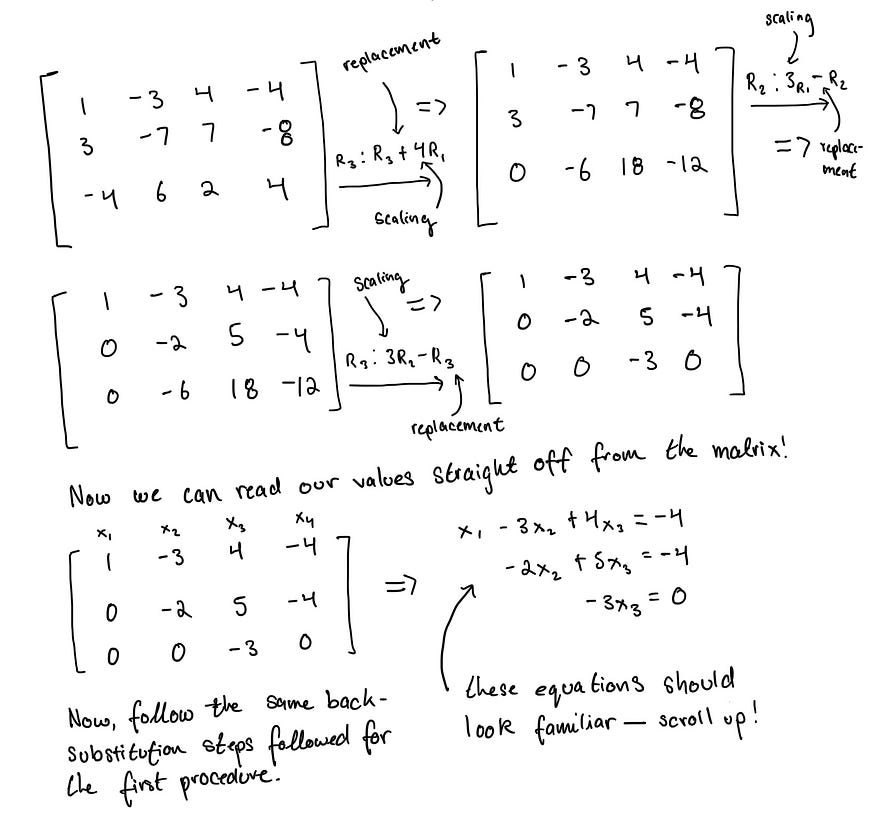
请注意,我使用了与线性方程方法完全相同的运算和比例因子。不出所料,我们最终得到了与以前相同的方程。其他需要注意的是最终矩阵左下角的三角形。这种模式的出现是有意义的,因为 0 是消除变量的标记,每个消除的变量都使我们更接近于确定可以轻松求解的方程;这反过来又使整个系统的解决方案取得进展。我们将重新审视这种情况,我将在下一章中为它提供一个更正式的定义。
九、总结
在本章中,我们学习了:
- 线性方程:具有一个或多个变量的方程,其中方程的次数必须等于 1。
- 线性方程组:线性方程组的集合。
- 一个或多个线性方程组的解:线性系统要么没有解,要么有唯一的解,要么有无限的解。
- 矩阵表示法:矩形数组,用作表示线性系统的压缩方式。
- 行操作:替换、交换和缩放操作允许我们将矩阵转换为已消除足够多的未知变量来为系统求解的矩阵。
- 求解线性系统:一种系统的方法,用于查找 a) 给定线性系统是否存在解,以及 b) 如果存在解,它们的确切值是多少。
参考资料:
数学
数学
线性代数
机
Linear Algebra 1: Linear Equations and Systems | by tenzin migmar (t9nz) | Sep, 2023 | Towards Data Science (medium.com)
相关文章:

线性代数1:线性方程和系统
Digital Collection (staedelmuseum.de) 图片来自施泰德博物馆 一、前言 通过这些文章,我希望巩固我对这些基本概念的理解,同时如果可能的话,通过我希望成为一种基于直觉的数学学习方法为其他人提供额外的清晰度。如果有任何错误或机会需要我…...
“第四十八天” 计算机组成原理
数据结构学完了,不过也就是匆匆过了一遍,后面肯定还是要重来的。现在开始学机组了。 计算机发展历程: 计算机硬件唯一能识别的数据是二进制的 0/1,而在计算机中用低/高电平表示 0 / 1,也就是通过电信号传递数据&#x…...

【算法|贪心算法系列No.4】leetcode55. 跳跃游戏 45. 跳跃游戏 II
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...

第九章 JDBC
文章目录 一. 单选题(共5题,50分)二. 判断题(共5题,50分) 一. 单选题(共5题,50分) (单选题) 下列选项,可用于存储结果集的对象是() A.…...
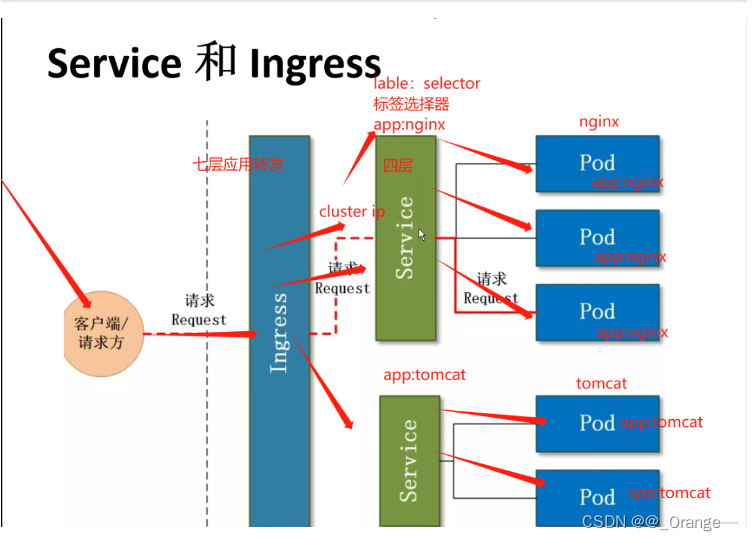
Kubernetes基础概念及架构和组件
目录 一、kubernetes简介 1、kubernetes的介绍与作用 2、为什么要用K8S? 二、kubernetes特性 1、自我修复 2、弹性伸缩 3、服务发现和负载均衡 4、自动发布(滚动发布/更新)和回滚 5、集中化配置管理和密钥管理 6、存储编排 7、任务批…...
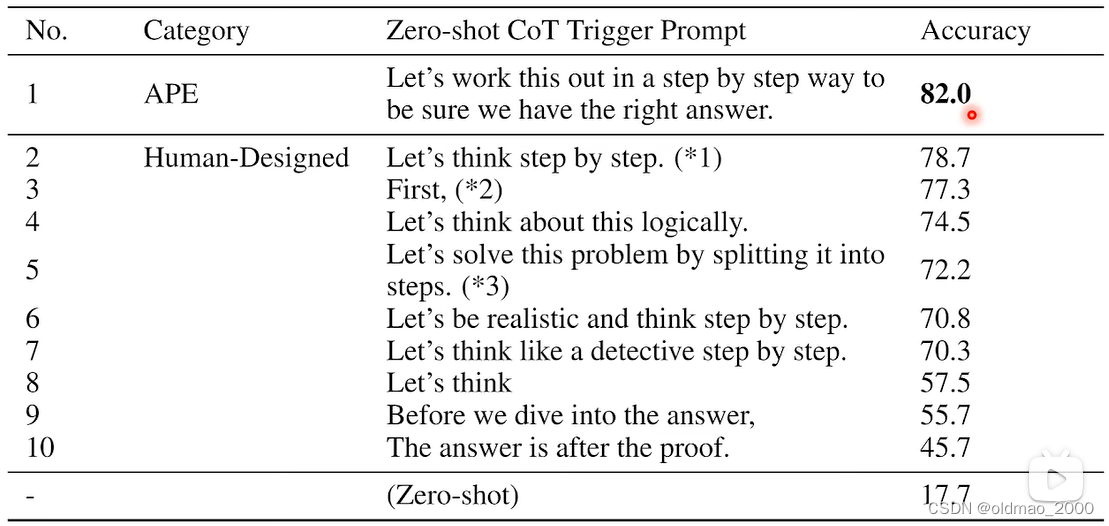
04.Finetune vs. Prompt
目录 语言模型回顾大模型的两种路线专才通才二者的比较 专才养成记通才养成记Instruction LearningIn-context Learning 自动Prompt 部分截图来自原课程视频《2023李宏毅最新生成式AI教程》,B站自行搜索 语言模型回顾 GPT:文字接龙 How are __. Bert&a…...
-采用NXOpen完成对象的合并操作)
UG NX二次开发(C#)-采用NXOpen完成对象的合并操作
文章目录 1、前言2、Ufun实现布尔和操作的函数2.1 函数说明2.2 源代码3、采用NXOpen实现布尔和操作的函数3.1 函数说明3.2 源代码4、测试结果4.1 采用UFun 与NXOpen的结果4.2采用UFun 与NXOpen的对比说明1、前言 在UG NX中开发过程中,创建特征对象的时候往往会用到布尔操作,…...

测开不得不会的python之re模块正则表达式匹配
学习目录 正则表达式介绍 正则表达式的常用符号 python的re模块 findall()函数 finditer()函数 match()函数 search()函数 split()函数 正则表达式的介绍 Python 通过标准库中的 re 模块来支持正则表达式。 正则表达式作为高级的文本模式匹配、抽取、和搜索。简单地说…...

selenium4 元素定位
selenium4 9种元素定位 ID driver.find_element(By.ID,"kw")NAME driver.find_element(By.NAME,"tj_settingicon")CLASS_NAME driver.find_element(By.CLASS_NAME,"ipt_rec")TAG_NAME driver.find_element(By.TAG_NAME,"area")LINK_T…...

sql高级教程-索引
文章目录 架构简介1.连接层2.服务层3.引擎层4.存储层 索引优化背景目的劣势分类基本语法索引结构和适用场景 性能分析MySq| Query Optimizerexplain 索引优化单表优化两表优化三表优化 索引失效原因 架构简介 1.连接层 最上层是一些客户端和连接服务,包含本地sock通…...
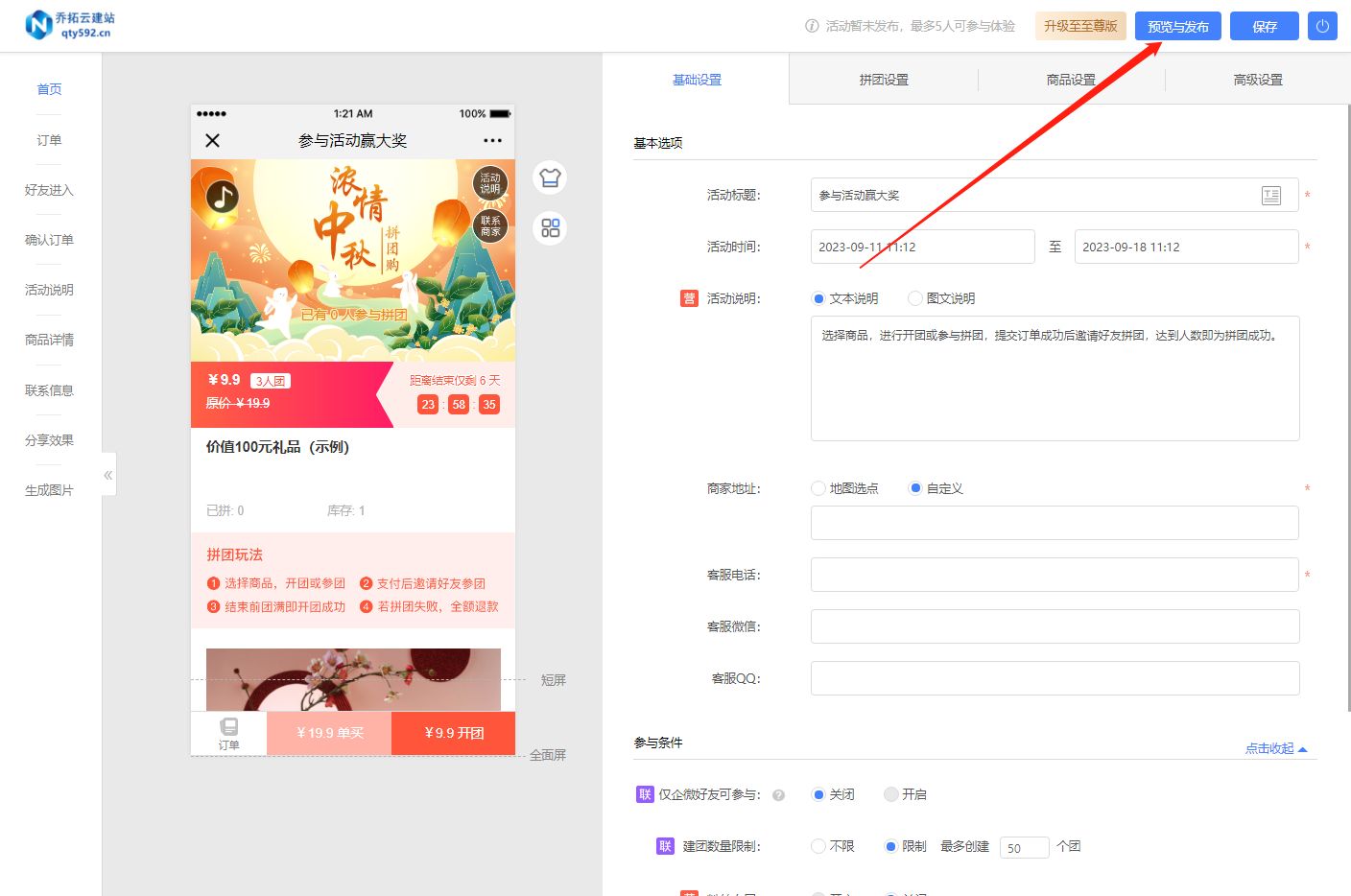
拼团小程序制作技巧大揭秘:零基础也能轻松掌握
随着拼团模式的日益流行,越来越多的商家和消费者开始关注拼团小程序的制作。对于没有技术背景的普通人来说,制作一个拼团小程序似乎是一项艰巨的任务。但实际上,选择一个简单易用的第三方平台或工具,可以轻松完成拼团小程序的制作…...

报错:The supplied javaHome seems to be invalid. I cannot find the java executable
AS 升级遇到的问题 问题 升级 Android Studio,碰到无法检测到 java The supplied javaHome seems to be invalid. I cannot find the java executable. Tried location: D:\Program Files\Android\Android Studio\jre\bin\java.exe 然后去网上找解决思路。 终于…...
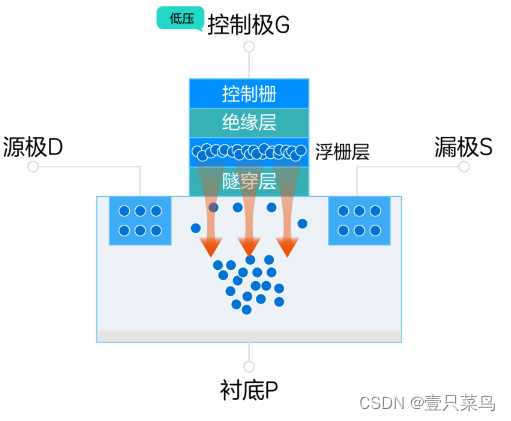
关于 硬盘
关于 硬盘 1. 机械硬盘1.1 基本概念1.2 工作原理1.3 寻址方式1.4 磁盘磁记录方式 2. 固态硬盘2.1 基本概念2.2 工作原理 1. 机械硬盘 1.1 基本概念 机械硬盘即是传统普通硬盘,硬盘的物理结构一般由磁头与盘片、电动机、主控芯片与排线等部件组成。 所有的数据都是…...
Java反射实体组装SQL
之前在LIS.Core定义了实体特性,在LIS.Model给实体类加了表特性,属性特性,外键特性等。ORM要实现增删改查和查带外键的父表信息就需要解析Model的特性和实体信息组装SQL来供数据库驱动实现增删改查功能。 实现实体得到SQL的工具类,…...

tensorrt安装使用教程
一般的深度学习项目,训练时为了加快速度,会使用多GPU分布式训练。但在部署推理时,为了降低成本,往往使用单个GPU机器甚至嵌入式平台(比如 NVIDIA Jetson)进行部署,部署端也要有与训练时相同的深…...
-- idea(2022版)将 已push 的 远程仓库 的 多条commit记录 进行撤销)
Java后端开发(十)-- idea(2022版)将 已push 的 远程仓库 的 多条commit记录 进行撤销
目录 1.多次 修改Test01类后,提交到本地仓库 。 2.多次重复 1 的步骤,多次commit成功后,在Git =》Log中会显示,commit记录...
常见面试题-Netty专栏(一)
typora-copy-images-to: imgs Netty 是什么呢?Netty 用于做什么呢? 答: Netty 是一个 NIO 客户服务端框架,可以快速开发网络应用程序,如协议服务端和客户端,极大简化了网络编程,如 TCP 和 UDP …...

【iOS】JSONModel的基本使用
文章目录 前言一、导入JSONModel二、JSONModel的基本使用1.基本用法2.模型集合3.模型导出为NSDictionary或JSON4.设置所有属性可选(所有属性值可以为空)5.下划线(蛇式)转驼峰命名法 前言 JSONModel 是一个用于 Objective-C 的开源库,它用于简…...
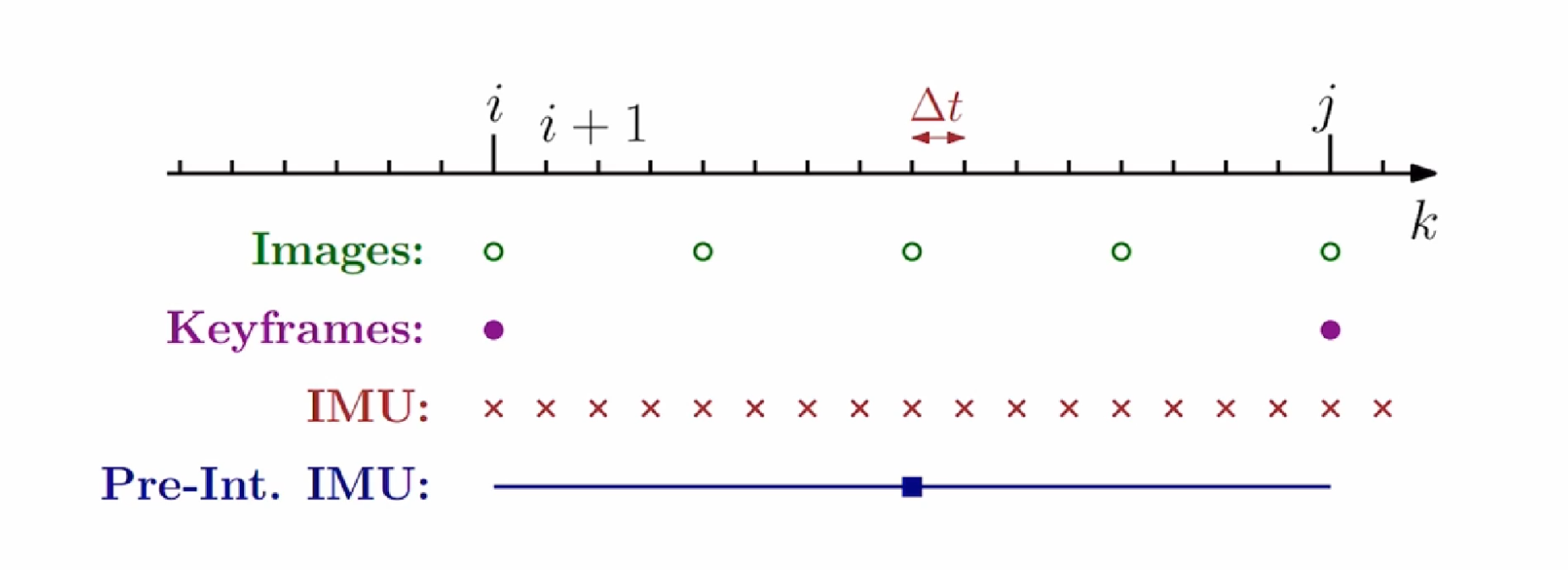
imu预积分学习(更新中)
imu预积分学习(更新中) IMU预积分可以做什么? 以上面那个经典图片为例子,IMU可以通过六轴数据,拿到第i帧和第j帧之间的相对位姿,这样不就可以去用来添加约束了吗 但是有一个比较大的问题是: I…...
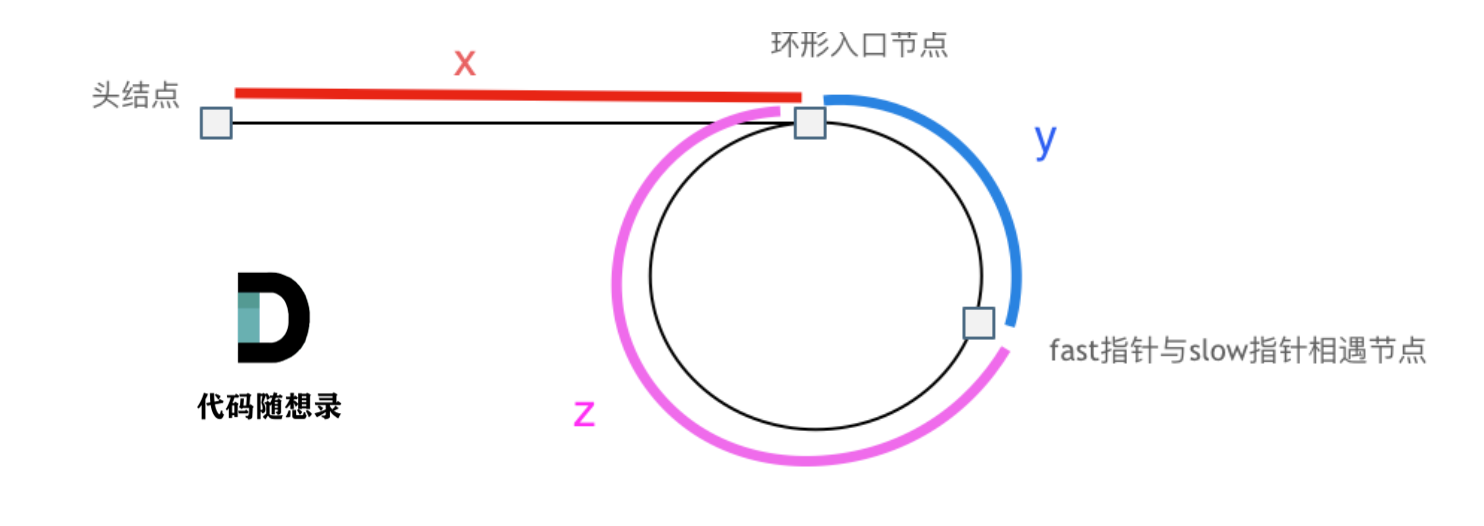
算法刷题-链表
算法刷题-链表 203. 移除链表元素 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出:[1,2,3,4,5]…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...
