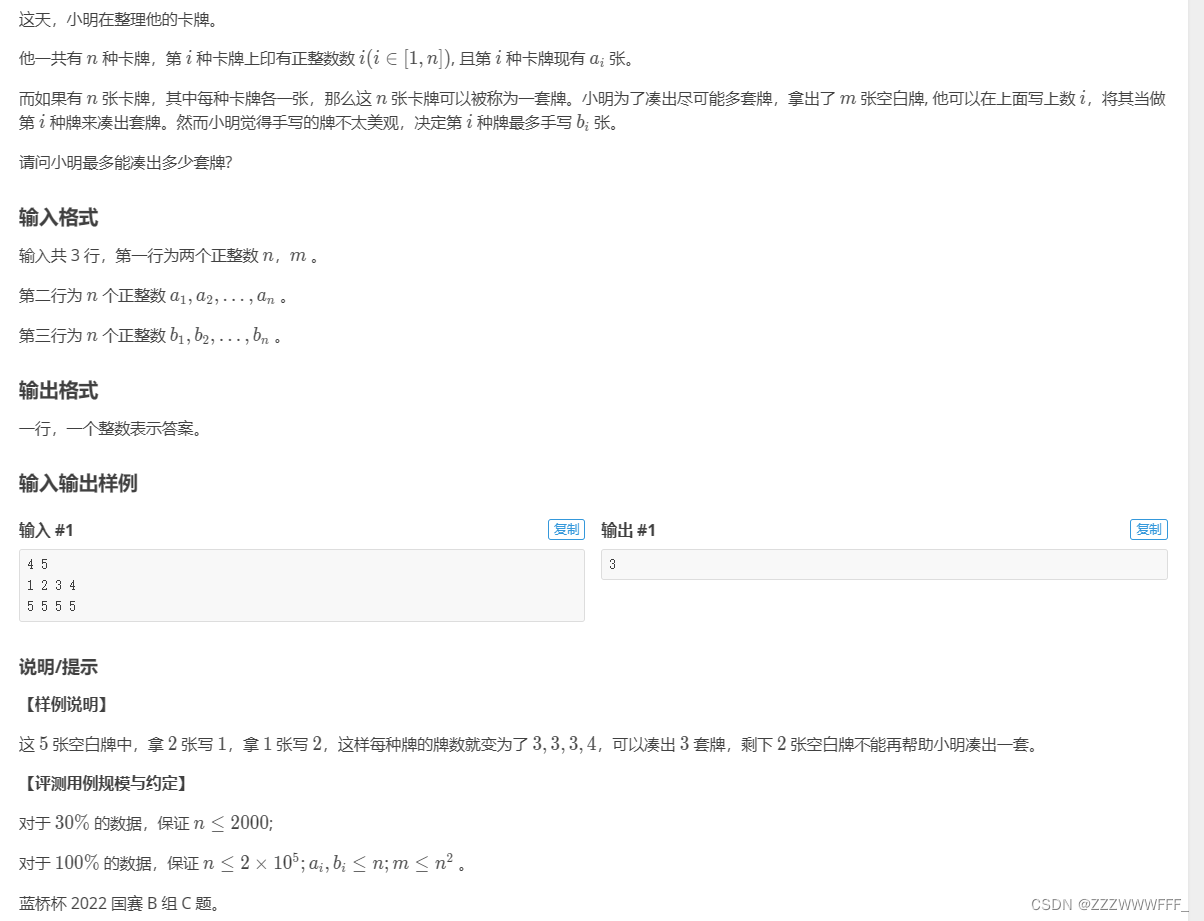
[蓝桥杯 2022 国 B] 卡牌(贪心/二分)
题目传送门
该题第一思路是想去模拟题目中所描述的过程
这里我选择从大到小遍历可能凑出的牌套数,计算凑出它需要补的牌数以及判断是否会超出能补的牌数
#include<iostream> #include<climits> #include<vector> #include<algorithm> #define int long long using namespace std;const int MAX=2e5+10;int a[MAX]; int b[MAX]; int n,m,ans=0,num=0; vector<int>v;signed main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];v.push_back(a[i]);}for(int i=1;i<=n;i++){cin>>b[i];}sort(v.begin(),v.end());//排序for(int i=n-1;i>=0;i--){//尝试将每一种卡牌都变成v[i]张 int ele=v[i];int sign=0;int sum=0; for(int j=1;j<=n;j++){int need=v[i]-a[j];//需要补上 if(need>0)sum+=need;if(b[j]-need<0){sign=1; break;//不能补 } }if(sum>m||sign){continue;}else{cout<<v[i]<<endl;break;}} return 0; }由于该算法效率低下并不能通过所有样例
但是仔细理解题意,我们可以发现该方法可以使用二分进行优化
#include<iostream> #include<algorithm> #define int long long using namespace std;const int MAX=2e5+10;int n,m,l,r; int a[MAX]; int b[MAX];bool check(int x){int s = 0;for (int i = 0; i < n; i++) {if (x - a[i] <= b[i]) {s += max(x - a[i], 0ll);//统计组成x套牌需要补s张牌}else return false;//超出了b[i]}if (s <= m) return true;//没有越界return false; }signed main(){cin>>n>>m;for(int i=0;i<n;i++){cin>>a[i];l = min(l, a[i]);}for(int i=0;i<n;i++){cin>>b[i];r=max(r,a[i]+b[i]);} int ans;while(l<=r){int mid=(l+r)/2;//二分组成的牌套数if(check(mid)){ans=mid;l=mid+1;}else{r=mid-1;}}cout<<ans<<endl;return 0; }
第二思路是使用“贪心”的思想进行解答
首先要理解一个东西,卡牌套数等于最少的卡牌牌数。因为一套卡牌需要所有卡牌各一张,所以对于最少的卡牌,它如果只有 x 张,则只能有 x 套卡牌含有最少的卡牌。再多的其他卡牌就没用了,所以卡牌套数等于最少的卡牌牌数。
那具体怎么贪心呢?使卡牌套数最多。由于卡牌套数等于最少的卡牌牌数,只需要尽量让最终各种卡牌数量接近即可。那就优先画数量少的卡牌,直到空卡牌用完。
每次 O(n) 选择最小的卡牌,复杂度会很高。由于这个贪心策略是要连续选择最小的,所以可以通过排序来降低复杂度。
最后还有一个问题:可画的卡牌数有限制。还是根据卡牌套数等于最少的卡牌牌数,在空卡牌够用的情况下,最终的卡牌套数取决于初始卡牌数与可画卡牌数的和最少的卡牌。所以可以判断目前求得的卡牌数是否大于每张卡牌初始卡牌数与可画卡牌数的和的最小值来解决这个问题。若小于,继续贪心。若大于,则证明空卡牌够用,但受可画的卡牌数的限制,卡牌套数只能为每张卡牌初始卡牌数与可画卡牌数的和的最小值。(好吧这一段有点难理解,可以结合代码里的注释理解)
#include<iostream> #include<algorithm> #include<climits> #define int long longconst int MAX=2e6;using namespace std;int n,m; int a[MAX]; int b;signed main(){int consume=0,minn=INT_MAX;cin>>n>>m;for(int i=0;i<n;i++){cin>>a[i];}for(int i=0;i<n;i++){cin>>b;if(a[i]+b<minn){minn=a[i]+b;//得到最大套牌数 } }sort(a,a+n);//其实无所谓对应下标 int ans=a[0];//初始值为最小牌数 for(int i=0;i<n;i++){if(i==n-1&&consume<m){ans+=(m-consume)/n;//剩余卡牌平均分 if(ans>minn)ans=minn;break; }if(a[i]<a[i+1]){//前面卡牌不够 //这里不能且无需去修改数组中的内容(会降低代码效率)consume+=(i+1)*(a[i+1]-a[i]);//消耗的卡牌ans+=(a[i+1]-a[i]); }if(consume>m)//不够牌补了{consume-=(i+1)*(a[i+1]-a[i]);ans-=(a[i+1]-a[i]);ans+=(m-consume)/(i+1);//平均分break; } if(ans>minn){ans=minn;break;}}cout<<ans<<endl;return 0; }
相关文章:

[蓝桥杯 2022 国 B] 卡牌(贪心/二分)
题目传送门 该题第一思路是想去模拟题目中所描述的过程 这里我选择从大到小遍历可能凑出的牌套数,计算凑出它需要补的牌数以及判断是否会超出能补的牌数 #include<iostream> #include<climits> #include<vector> #include<algorithm> #def…...
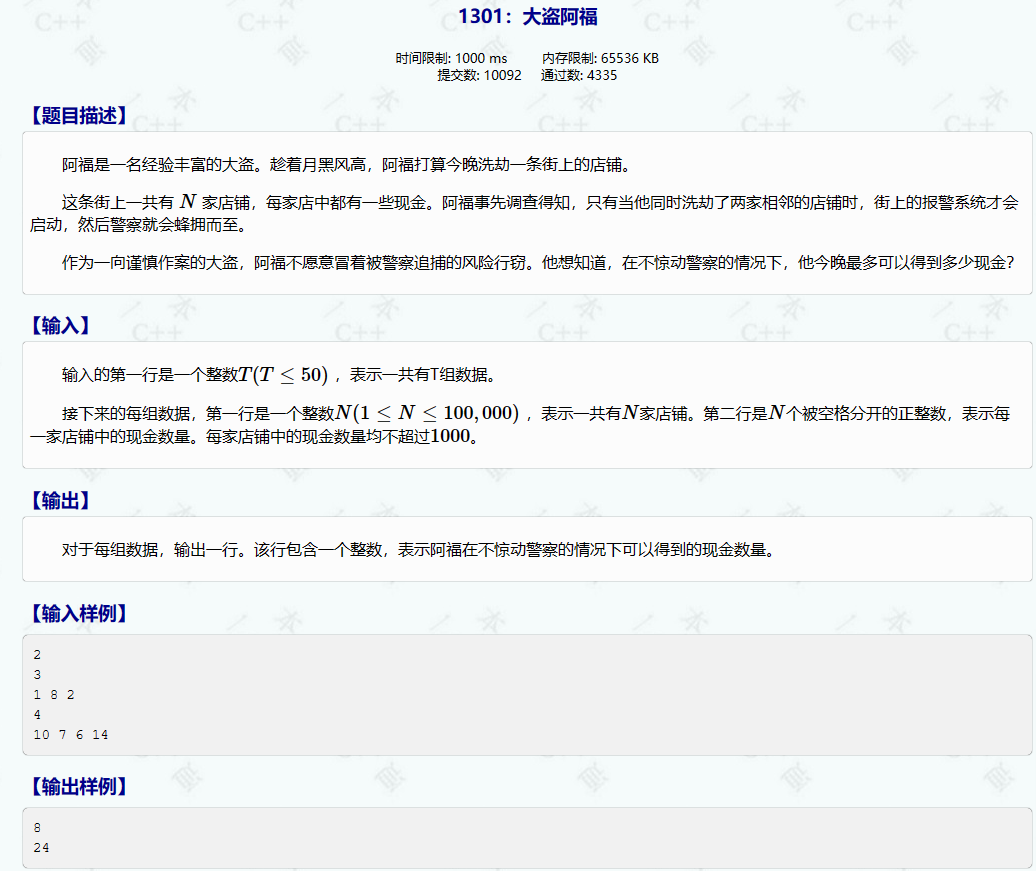
1301:大盗阿福
经典的dp打家劫舍问题状态设计dp[i][0]:在前i个店铺中选,且不选第i家的最大和dp[i][1]:在前i个店铺中选,且选第i家的最大和状态转移dp[i][0] max(dp[i-1][1], dp[i-1][0];第i家店不选,那么我们可以选第i-1个店 也可以…...
Netty——序列化的作用及自定义协议
序列化的作用及自定义协议序列化的重要性大小对比效率对比自定义协议序列化数据结构自定义编码器自定义解码器安全性验证NettyClientNettyServerNettyClientTestHandlerNettyServerTestHandler结果上一章已经说了怎么解决沾包和拆包的问题,但是这样离一个成熟的通信…...
)
一起Talk Android吧(第五百零五回:如何调整组件在约束布局中的大小)
文章目录 背景介绍调整方法各位看官们大家好,上一回中咱们说的例子是"如何调整组件在约束布局中的位置",这一回中咱们说的例子是" 如何调整组件在约束布局中的大小"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍 在使用约束(constraintl…...

【数据库】数据库的完整性
第五章 数据库完整性 数据库完整性 数据库的完整性是指数据的正确性和相容性 数据的正确性是指数据是符合现实世界语义,反映当前实际状况的数据的相容性是指数据库的同一对象在不同的关系中的数据是符合逻辑的 关系模型中有三类完整性约束:实体完整性…...

基因净化车间装修设计方案SICOLAB
基因净化车间的设计方案应该根据实际需求进行定制,以下是一些规划建设要点和洁净设计要注意的事项:一、净化车间规划建设要点:(1)基因车间的面积应该根据实验项目的规模进行规划,包括充足的操作区域和足够的…...
java 内部类的四种“写法”
基本介绍语法格式分类成员内部类静态内部类局部内部类匿名内部类(🐂🖊)一、基本介绍 : 1.概述当一个类的内部又完整地嵌套了另一个类时,被嵌套于内部的“内核”我们称之为“内部类”(inner class);而包含该…...

【python】main方法教程
嗨害大家好鸭! 我是小熊猫~ 首先 if name "main": 可以看成是python程序的入口, 就像java中的main()方法, 但不完全正确。 事实上python程序是从上而下逐行运行的, 在.py文件中, 除…...

公司对不同职级能力抽象要求的具体化
要先把当前级别要求的能力提升到精通,然后尝试做下一级别的事情。 但可能不确定高一级的能力要求究竟怎样,不同Title,如“工程师”“高级工程师”和“资深工程师”等。但这样 Title 对我们理解不同级别的能力要求,完全无用。“高…...

Java之MinIO存储桶和对象API使用
环境搭建 创建一个 maven项目,引入依赖: <!-- minio依赖--><dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.3.3</version></dependency><!-- 官方 minio…...

如何用java实现同时进行多个请求,可以将它们并行执行,从而减少总共的请求时间。
1.使用线程池 通过使用Java提供的线程池,可以将多个请求分配到不同的线程中并行执行。可以通过创建固定数量的线程池,然后将请求分配给线程池来实现。线程池会自动管理线程的数量和复用,从而减少了线程创建和销毁的开销,提高了程序…...
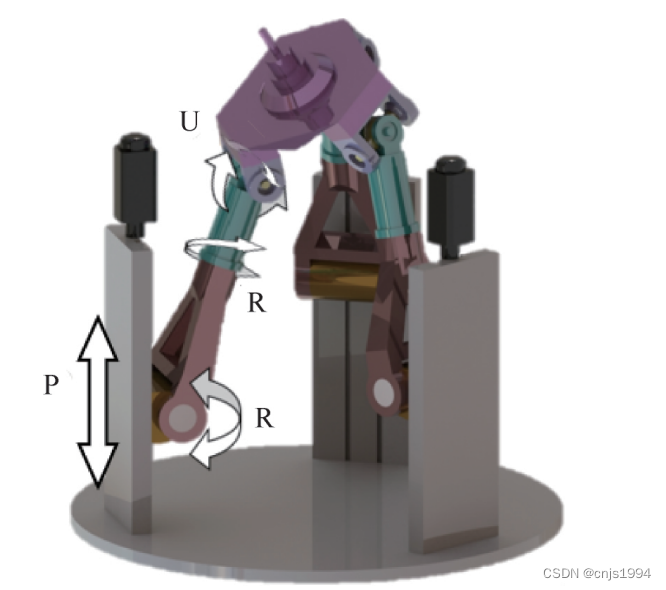
高端装备的AC主轴头结构
加工机器人的AC主轴头和位置相关动力学特性1. 位置依赖动态特性及其复杂性2. AC主轴头2.1 常见主轴头摆角结构2.2 摆动机构3. 加装AC主轴头的作用和局限性4. 切削机器人的减速器类型5. 其他并联结构形式参考文献资料1. 位置依赖动态特性及其复杂性 However, FRF measurements …...
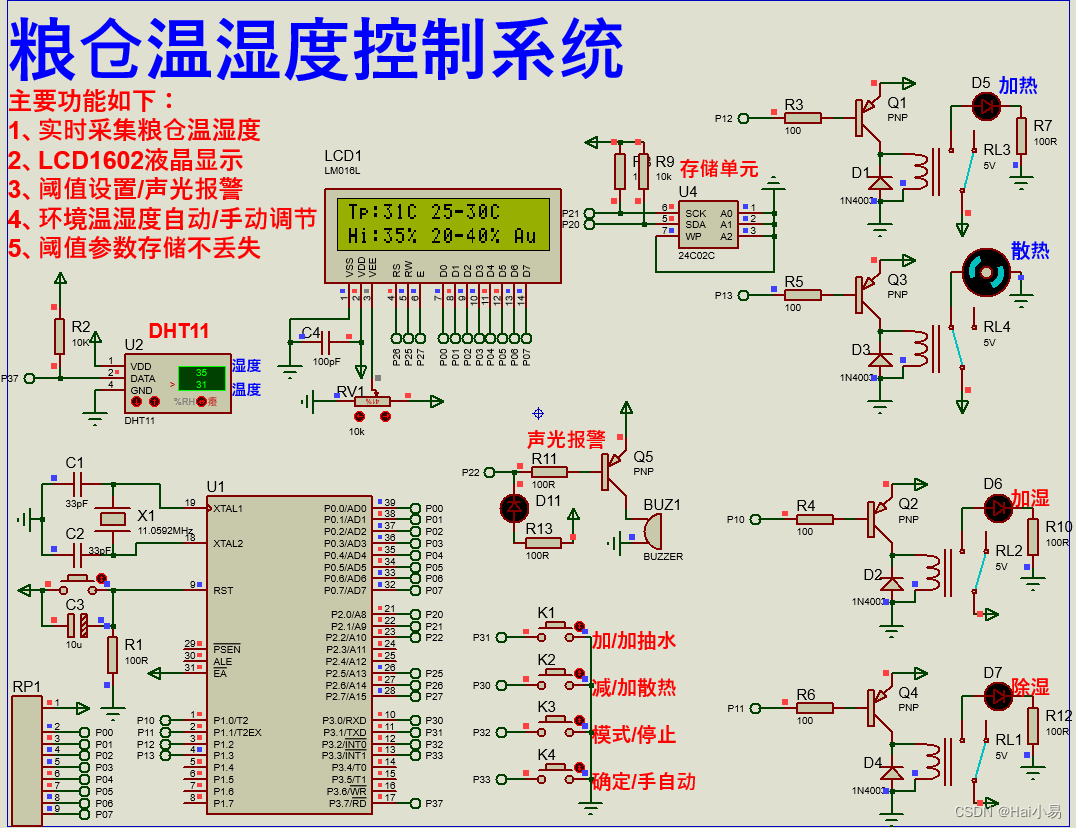
【Proteus仿真】【51单片机】粮仓温湿度控制系统设计
文章目录一、功能简介二、软件设计三、实验现象联系作者一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用声光报警模块、LCD1602显示模块、DHT11温湿度模块、继电器模块、加热加湿除湿风扇等。 主要功能: 系统运行后,LCD1602显示传…...
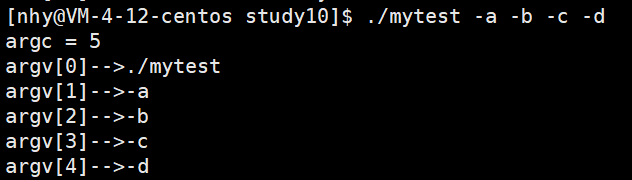
【LINUX】环境变量以及main函数的参数
文章目录前言环境变量常见环境变量:设置环境变量:和环境变量相关的命令:环境变量的组织方式:获取环境变量环境变量可以被子进程继承环境变量总结main函数的参数前言 大家好久不见,今天分享的内容是环境变量和main函数…...

使用Pyparsing为嵌入式开发定义自己的脚本语言
Python在嵌入式开发中也很流行生成实用脚本。Pyparsing还允许你轻松地定义在Python上下文中运行的定制脚本语言。Python实现的系统旨在能够独立执行用户传递的一系列命令。你希望系统以脚本的形式接收命令。用户应该能够定义条件。这种对通信中逻辑元素的最初简单的声音要求&am…...
)
C win32基础学习(二)
上一篇我们已经介绍了关于窗口程序的一些基本知识。从本篇开始我们将正式进入C win32的学习中去。 正文 窗口创建过程 定义WinMain函数 定义窗口处理函数(自定义,处理消息) 注册窗口类(向操作系统写入一些数据) 创建窗口(内存…...

理论五:控制反转、依赖反转、依赖注入,这三者有何区别和联系?
关于SOLID原则,我们已经学过单一职责、开闭、里式替换、接口隔离这四个原则。今天,我们再来学习最后一个原则:依赖反转原则。在前面几节课中,我们讲到,单一职责原则和开闭原则的原理比较简单,但是,想要在实践中用好却比较难。而今天我们要讲到的依赖反转原则正好相反。这个原则…...
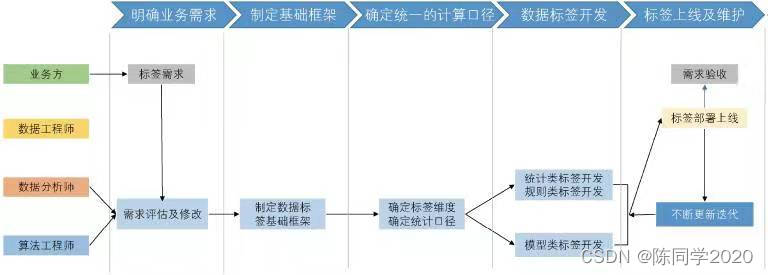
读书笔记//《数据分析之道》
出版时间:2022年 作者曾在互联网大厂做数据分析。从举例可以洞见作者的工作经历。 点评:作者在数据分析领域非常资深,尝试在书中提供一个数据分析工作框架参考。书本内容有点感觉是ppt的集合,辅以案例说明。不过,干货还…...
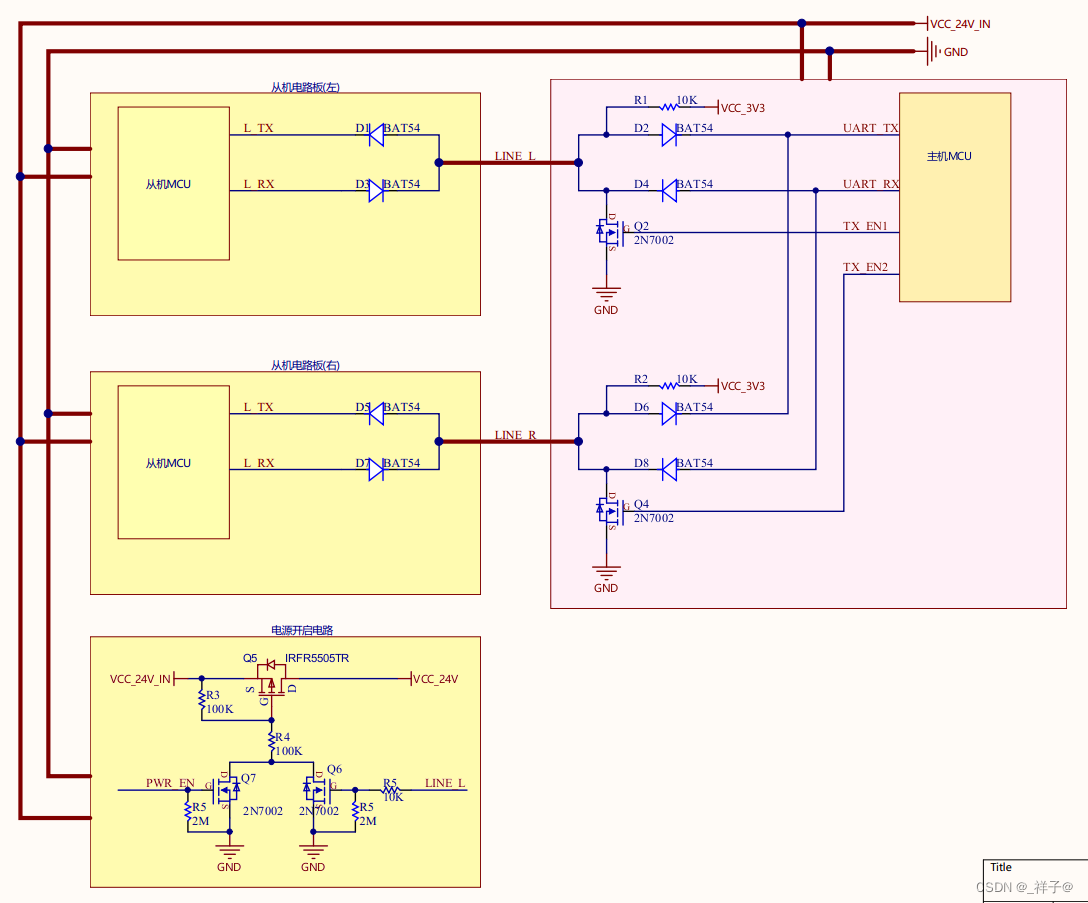
1个串口用1根线实现多机半双工通信+开机控制电路
功能需求: 主机使用一个串口,与两个从机进行双向通信,主机向从机发送数据,从机能够返回数据,由于结构限制,主机与从机之间只有3根线(电源、地、数据线),并且从机上没有设…...
KUKA机器人外部自动运行模式的相关信号配置
KUKA机器人外部自动运行模式的相关信号配置 通过例如PLC这样的控制器来进行外部自动运行控制时,运行接口向机器人控制系统发出机器人进程的相关信号(例如运行许可、故障确认、程序启动等),机器人向上级控制系统发送有关运行状态和故障状态的信息。 必需的配置: 配置CEL…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
