Leetcode.2385 感染二叉树需要的总时间
题目链接
Leetcode.2385 感染二叉树需要的总时间 Rating : 1711
题目描述
给你一棵二叉树的根节点 root,二叉树中节点的值 互不相同 。另给你一个整数 start。在第 0分钟,感染 将会从值为 start的节点开始爆发。
每分钟,如果节点满足以下全部条件,就会被感染:
- 节点此前还没有感染。
- 节点与一个已感染节点相邻。
返回感染整棵树需要的分钟数。
示例 1:
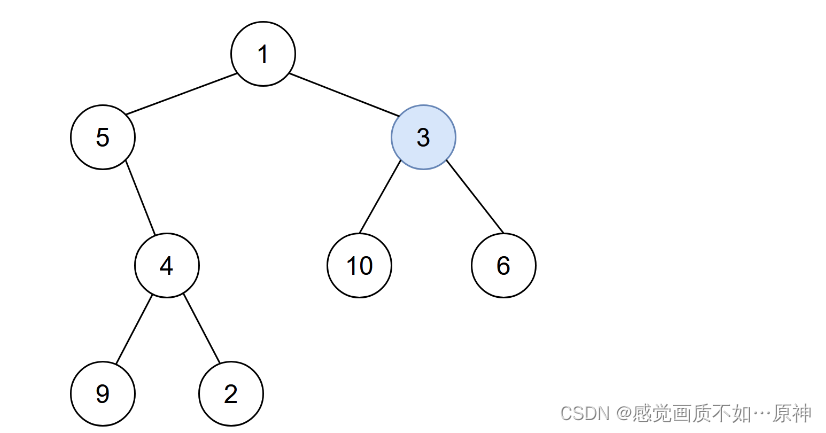
输入:root = [1,5,3,null,4,10,6,9,2], start = 3
输出:4
解释:节点按以下过程被感染:
- 第 0 分钟:节点 3
- 第 1 分钟:节点 1、10、6
- 第 2 分钟:节点5
- 第 3 分钟:节点 4
- 第 4 分钟:节点 9 和 2 感染整棵树需要 4 分钟,所以返回 4 。
示例 2:

输入:root = [1], start = 1
输出:0
解释:第 0 分钟,树中唯一一个节点处于感染状态,返回 0 。
提示:
- 树中节点的数目在范围 [1, 10510^5105] 内
- 1<=Node.val<=1051 <= Node.val <= 10^51<=Node.val<=105
- 每个节点的值 互不相同
- 树中必定存在值为
start的节点
解法一:DFS建图 + BFS
用一个集合 g保存 图的边,在 DFS 的过程中,加入边。例如 1 -> 5 , 5 -> 1 , 1 -> 3 , 3 -> 1。
接着再从起点 start开始 BFS 求最短的路径,即感染整棵树的时间。
时间复杂度:O(n)O(n)O(n)
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public://g 用来存储图的边unordered_map<int,vector<int>> g;//dfs 建图void dfs(TreeNode* root){if(root==nullptr) return;int a = root->val;if(root->left != nullptr){int b = root->left->val;g[a].push_back(b);g[b].push_back(a);} if(root->right != nullptr){int b = root->right->val;g[a].push_back(b);g[b].push_back(a);}dfs(root->left);dfs(root->right);}int amountOfTime(TreeNode* root, int start) {dfs(root);queue<int> q;//记录已经被感染过的点unordered_set<int> vis;int ans = 0;//加入起点q.push(start);vis.insert(start);//bfs 求整棵树被感染的时间 就是求 从 start 开始的最长路径。while(!q.empty()){int sz = q.size();for(int i = 0;i < sz;i++){auto u = q.front();q.pop();for(auto v:g[u]){if(vis.count(v)) continue;vis.insert(v);q.push(v);}}ans++;}return ans - 1;}
};
解法二:DFS
当 start是根结点时,整棵树被感染的时间就是树的高度(1)。
当 start不是根结点时,整棵树被感染的时间就是 以start为根结点的树的高度 和 start到根结点的距离加上 + 另一棵子树的高度,这两者取最大值。
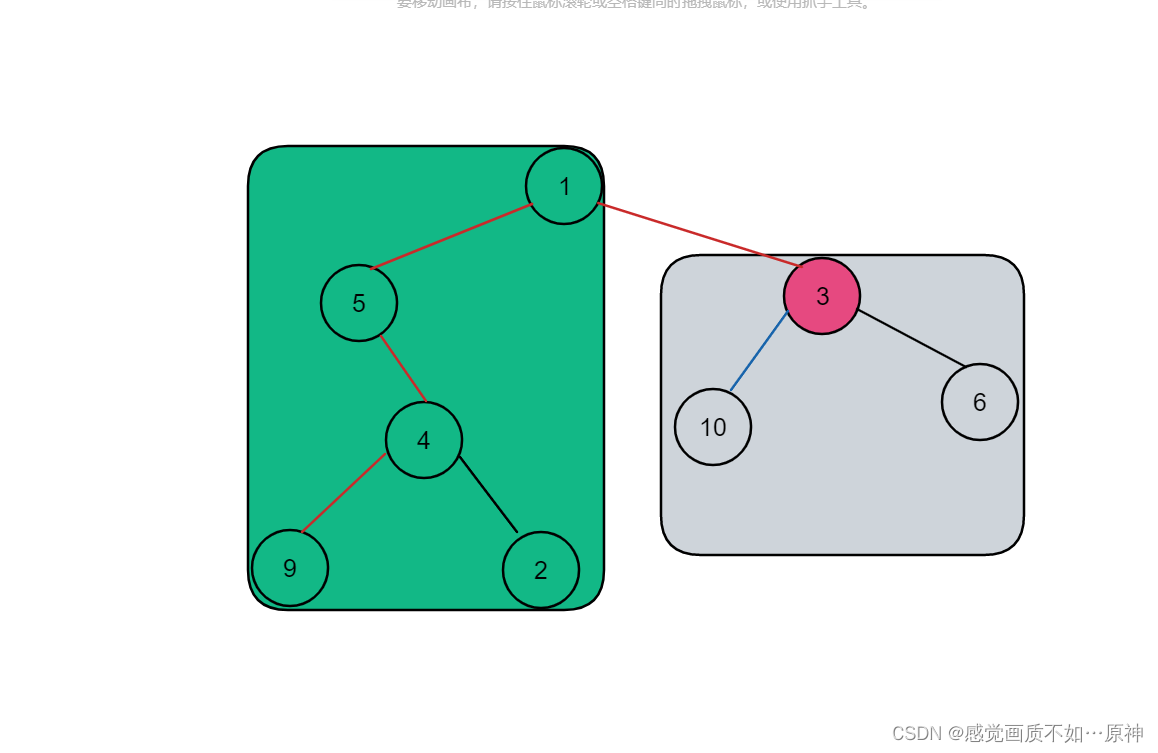
时间复杂度:O(n)O(n)O(n)
代码:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int depth = -1;int ans = 0;//返回以 root 为根结点的树高度 int dfs(TreeNode* root,int level,int start){if(root == nullptr) return 0;//先搜左子树,l 是左子树的高度int l = dfs(root->left,level + 1,start);//记录初始感染结点在第 几 层if(root->val == start) depth = level;//判断初始感染结点是否在左子树bool inLeft = depth != -1;//再搜右子树 , r 是右子树的高度int r = dfs(root->right,level+1,start);//如果此时遇到 start ,就先记录 以它为根结点的树高 , 因为我们是自底向上递归的,所以 l 和 r//现在时已经计算出来的了if(root->val == start) ans = max(ans,max(l,r));//如果start在左子树,那就更新 当前结点到根结点的距离 + 根结点右子树的距离。start在右子树也是//一样的逻辑//需要注意的是,实际上更新的答案应该是 当前结点 cur 回溯到根结点时,此时的level = 0,depth我们递归的过程中已经记录下来了,此时根结点root 的右子树高度r 才是整棵树右子树的高度//此时的 depth - level + r 才是我们最终需要的答案,但是实际上这些中间过程的结点产生的答案也并不会影响我们最终的答案。if(inLeft) ans = max(ans,depth - level + r);else ans = max(ans,depth - level + l);return max(l,r)+1;}int amountOfTime(TreeNode* root, int start) {dfs(root,0,start);return ans;}
};
相关文章:

Leetcode.2385 感染二叉树需要的总时间
题目链接 Leetcode.2385 感染二叉树需要的总时间 Rating : 1711 题目描述 给你一棵二叉树的根节点 root,二叉树中节点的值 互不相同 。另给你一个整数 start。在第 0分钟,感染 将会从值为 start的节点开始爆发。 每分钟,如果节点…...

[蓝桥杯 2022 国 B] 卡牌(贪心/二分)
题目传送门 该题第一思路是想去模拟题目中所描述的过程 这里我选择从大到小遍历可能凑出的牌套数,计算凑出它需要补的牌数以及判断是否会超出能补的牌数 #include<iostream> #include<climits> #include<vector> #include<algorithm> #def…...
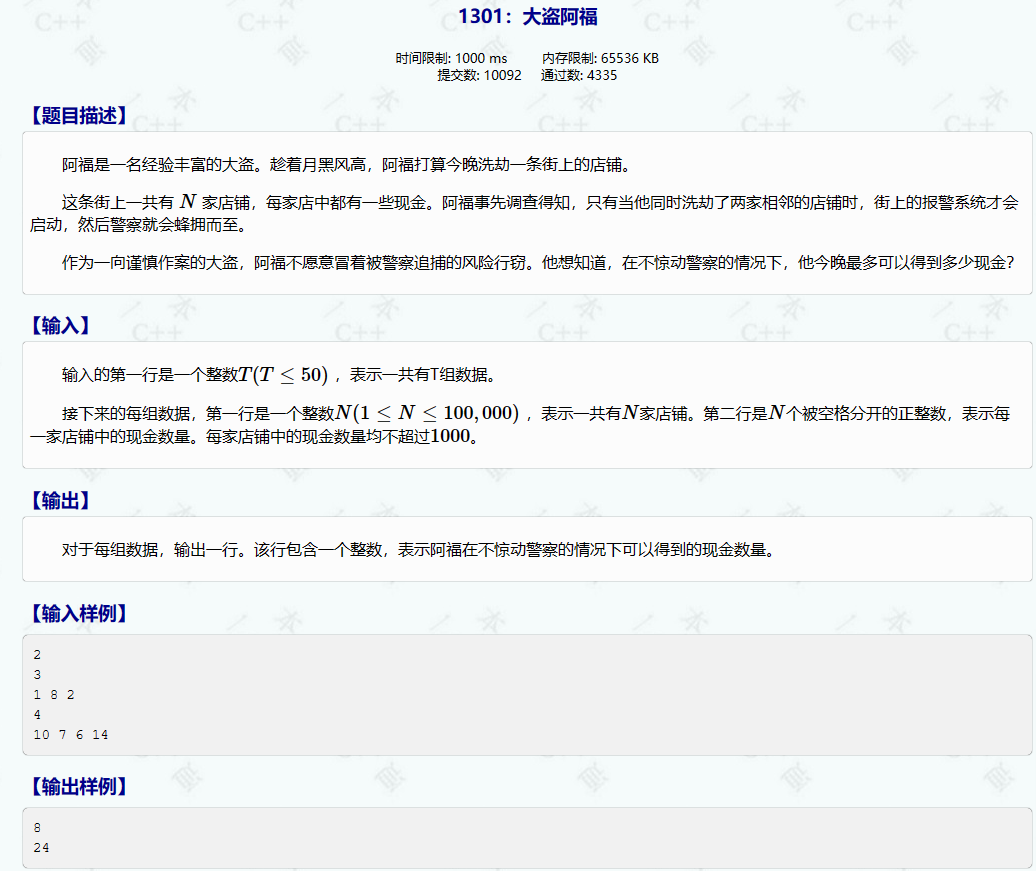
1301:大盗阿福
经典的dp打家劫舍问题状态设计dp[i][0]:在前i个店铺中选,且不选第i家的最大和dp[i][1]:在前i个店铺中选,且选第i家的最大和状态转移dp[i][0] max(dp[i-1][1], dp[i-1][0];第i家店不选,那么我们可以选第i-1个店 也可以…...
Netty——序列化的作用及自定义协议
序列化的作用及自定义协议序列化的重要性大小对比效率对比自定义协议序列化数据结构自定义编码器自定义解码器安全性验证NettyClientNettyServerNettyClientTestHandlerNettyServerTestHandler结果上一章已经说了怎么解决沾包和拆包的问题,但是这样离一个成熟的通信…...
)
一起Talk Android吧(第五百零五回:如何调整组件在约束布局中的大小)
文章目录 背景介绍调整方法各位看官们大家好,上一回中咱们说的例子是"如何调整组件在约束布局中的位置",这一回中咱们说的例子是" 如何调整组件在约束布局中的大小"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍 在使用约束(constraintl…...

【数据库】数据库的完整性
第五章 数据库完整性 数据库完整性 数据库的完整性是指数据的正确性和相容性 数据的正确性是指数据是符合现实世界语义,反映当前实际状况的数据的相容性是指数据库的同一对象在不同的关系中的数据是符合逻辑的 关系模型中有三类完整性约束:实体完整性…...

基因净化车间装修设计方案SICOLAB
基因净化车间的设计方案应该根据实际需求进行定制,以下是一些规划建设要点和洁净设计要注意的事项:一、净化车间规划建设要点:(1)基因车间的面积应该根据实验项目的规模进行规划,包括充足的操作区域和足够的…...
java 内部类的四种“写法”
基本介绍语法格式分类成员内部类静态内部类局部内部类匿名内部类(🐂🖊)一、基本介绍 : 1.概述当一个类的内部又完整地嵌套了另一个类时,被嵌套于内部的“内核”我们称之为“内部类”(inner class);而包含该…...

【python】main方法教程
嗨害大家好鸭! 我是小熊猫~ 首先 if name "main": 可以看成是python程序的入口, 就像java中的main()方法, 但不完全正确。 事实上python程序是从上而下逐行运行的, 在.py文件中, 除…...

公司对不同职级能力抽象要求的具体化
要先把当前级别要求的能力提升到精通,然后尝试做下一级别的事情。 但可能不确定高一级的能力要求究竟怎样,不同Title,如“工程师”“高级工程师”和“资深工程师”等。但这样 Title 对我们理解不同级别的能力要求,完全无用。“高…...

Java之MinIO存储桶和对象API使用
环境搭建 创建一个 maven项目,引入依赖: <!-- minio依赖--><dependency><groupId>io.minio</groupId><artifactId>minio</artifactId><version>8.3.3</version></dependency><!-- 官方 minio…...

如何用java实现同时进行多个请求,可以将它们并行执行,从而减少总共的请求时间。
1.使用线程池 通过使用Java提供的线程池,可以将多个请求分配到不同的线程中并行执行。可以通过创建固定数量的线程池,然后将请求分配给线程池来实现。线程池会自动管理线程的数量和复用,从而减少了线程创建和销毁的开销,提高了程序…...
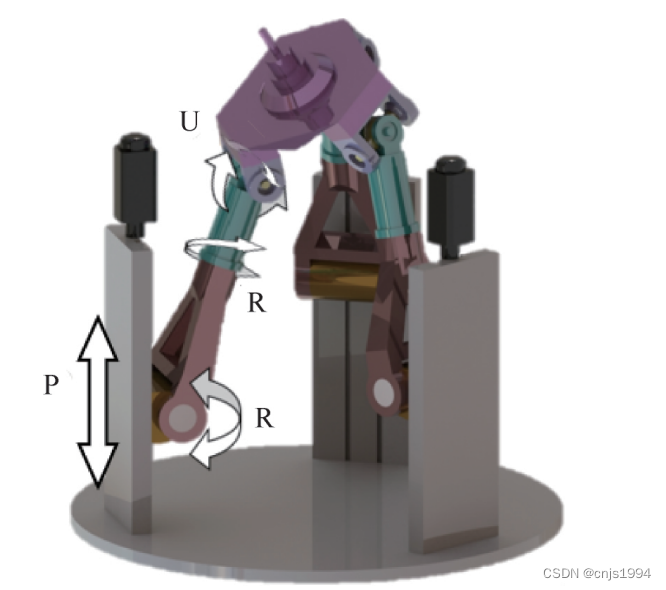
高端装备的AC主轴头结构
加工机器人的AC主轴头和位置相关动力学特性1. 位置依赖动态特性及其复杂性2. AC主轴头2.1 常见主轴头摆角结构2.2 摆动机构3. 加装AC主轴头的作用和局限性4. 切削机器人的减速器类型5. 其他并联结构形式参考文献资料1. 位置依赖动态特性及其复杂性 However, FRF measurements …...
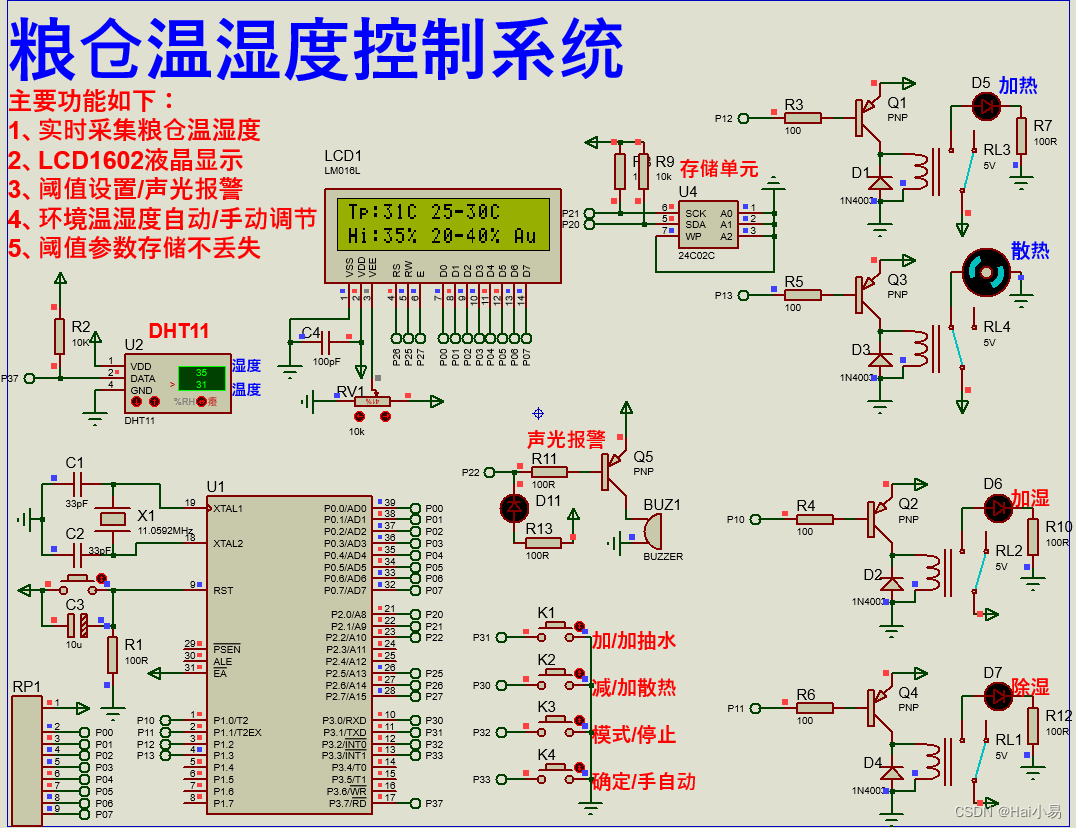
【Proteus仿真】【51单片机】粮仓温湿度控制系统设计
文章目录一、功能简介二、软件设计三、实验现象联系作者一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用声光报警模块、LCD1602显示模块、DHT11温湿度模块、继电器模块、加热加湿除湿风扇等。 主要功能: 系统运行后,LCD1602显示传…...
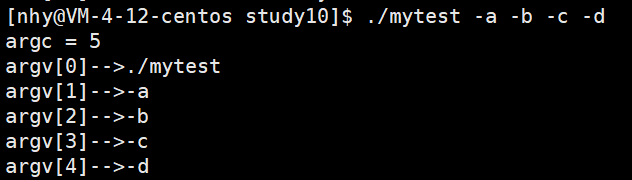
【LINUX】环境变量以及main函数的参数
文章目录前言环境变量常见环境变量:设置环境变量:和环境变量相关的命令:环境变量的组织方式:获取环境变量环境变量可以被子进程继承环境变量总结main函数的参数前言 大家好久不见,今天分享的内容是环境变量和main函数…...

使用Pyparsing为嵌入式开发定义自己的脚本语言
Python在嵌入式开发中也很流行生成实用脚本。Pyparsing还允许你轻松地定义在Python上下文中运行的定制脚本语言。Python实现的系统旨在能够独立执行用户传递的一系列命令。你希望系统以脚本的形式接收命令。用户应该能够定义条件。这种对通信中逻辑元素的最初简单的声音要求&am…...
)
C win32基础学习(二)
上一篇我们已经介绍了关于窗口程序的一些基本知识。从本篇开始我们将正式进入C win32的学习中去。 正文 窗口创建过程 定义WinMain函数 定义窗口处理函数(自定义,处理消息) 注册窗口类(向操作系统写入一些数据) 创建窗口(内存…...

理论五:控制反转、依赖反转、依赖注入,这三者有何区别和联系?
关于SOLID原则,我们已经学过单一职责、开闭、里式替换、接口隔离这四个原则。今天,我们再来学习最后一个原则:依赖反转原则。在前面几节课中,我们讲到,单一职责原则和开闭原则的原理比较简单,但是,想要在实践中用好却比较难。而今天我们要讲到的依赖反转原则正好相反。这个原则…...
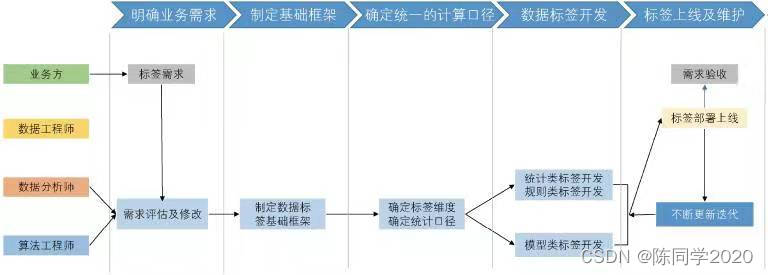
读书笔记//《数据分析之道》
出版时间:2022年 作者曾在互联网大厂做数据分析。从举例可以洞见作者的工作经历。 点评:作者在数据分析领域非常资深,尝试在书中提供一个数据分析工作框架参考。书本内容有点感觉是ppt的集合,辅以案例说明。不过,干货还…...
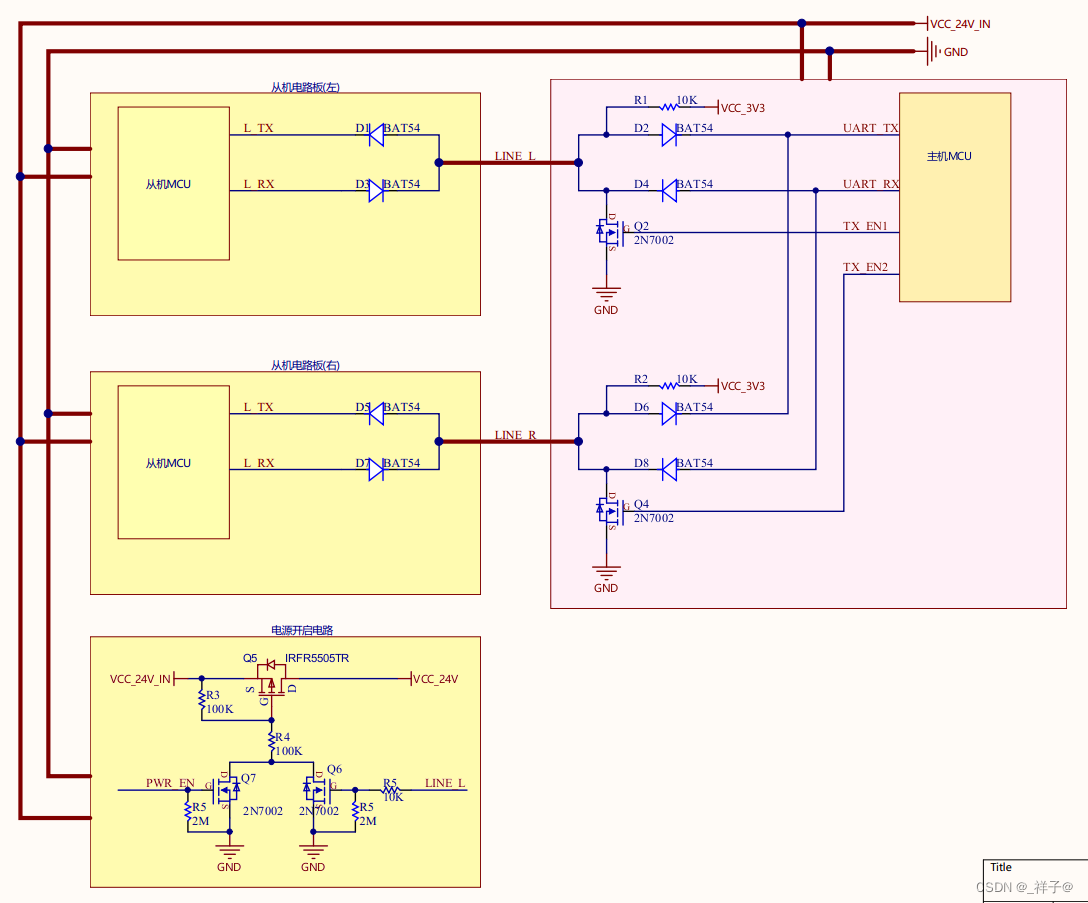
1个串口用1根线实现多机半双工通信+开机控制电路
功能需求: 主机使用一个串口,与两个从机进行双向通信,主机向从机发送数据,从机能够返回数据,由于结构限制,主机与从机之间只有3根线(电源、地、数据线),并且从机上没有设…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
