2316. 统计无向图中无法互相到达点对数

2316. 统计无向图中无法互相到达点对数
难度: 中等
来源: 每日一题 2023.10.21
给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。
请你返回 无法互相到达 的不同 点对数目 。
示例 1:
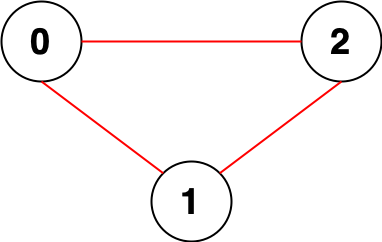
输入:n = 3, edges = [[0,1],[0,2],[1,2]]
输出:0
解释:所有点都能互相到达,意味着没有点对无法互相到达,所以我们返回 0 。
示例 2:
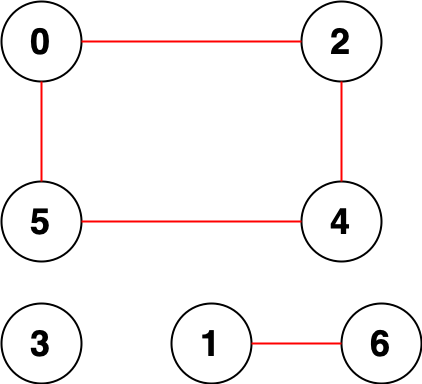
输入:n = 7, edges = [[0,2],[0,5],[2,4],[1,6],[5,4]]
输出:14
解释:总共有 14 个点对互相无法到达:
[[0,1],[0,3],[0,6],[1,2],[1,3],[1,4],[1,5],[2,3],[2,6],[3,4],[3,5],[3,6],[4,6],[5,6]]
所以我们返回 14 。
提示:
1 <= n <= 10^50 <= edges.length <= 2 * 10^5edges[i].length == 20 <= ai, bi < nai != bi- 不会有重复边。
class StockSpanner {public long countPairs(int n, int[][] edges) {}
}
分析与题解
-
邻接表 + 深度优先遍历
这个题目其实就是对无向图的邻接表的理解, 那么求两个点没有任何关联, 我们只要如果只要求出一条完整的边, 那么剩下所有的节点一定与这条完整的边不连接, 不连接的含义就是这条边上的节点与剩下的所有节点都是两两无法相互到达.
那么基于这样的理论, 我们假设这条边上的节点个数是
m个, 那么对于这条边上的所有节点与剩下的节点两两无法相互到达的组合个数为m * (n - m).另外, 假设
节点1和节点2无法相互到达, 那么深度优先遍历节点1时,会计算一遍节点1和节点2; 深度优先遍历节点1时, 同样会计算一遍节点1和节点2. 所以最终结果我们需要除以2.接下来, 我们看一下具体的解题过程.
首先, 我们先创建无向图的邻接表, 这里我使用的是HashMap来作为邻接表的存储空间.
// 创建邻接表 HashMap<Integer, ArrayList<Integer>> cache = new HashMap<>(); for(int i = 0; i < n; i++) {cache.put(i, new ArrayList<>()); } for(int[] item: edges) {Integer first = item[0];Integer second = item[1];cache.get(first).add(second);cache.get(second).add(first); }然后通过深度优先遍历查找每一条边符合题目的个数.
// 深度优先遍历 // 当我们找到一个完整链路节点, 那么这些节点就不可能和剩下的节点有链接了 // 假设找到某条无线边的所有节点为m个, 总结点数为n个. 那么相互不能到达的两两节点数为 m * (n - m) boolean[] visited = new boolean[n]; long result = 0; for(Integer key : cache.keySet()) {if(!visited[key]) {long count = dfs(key, cache, visited);result += (n - count) * count;} }对于深度优先遍历, 我们就没有啥好说的, 我们只需要按照常规方式进行递归即可.
public int dfs(Integer key, HashMap<Integer, ArrayList<Integer>> cache, boolean[] visited) {if(visited[key]) {return 0;}visited[key] = true;int count = 1;ArrayList<Integer> group = cache.get(key);for(Integer item : group) {if(visited[item] == false) {count += dfs(item, cache, visited);}}return count; }然后最后的计算结果因为所有的个数都计算了两遍, 我们需要除以2来求出最终的结果.
return result/2;最后, 我们一起看一下整体的代码逻辑.
class Solution {public long countPairs(int n, int[][] edges) {// 创建邻接表HashMap<Integer, ArrayList<Integer>> cache = new HashMap<>();for(int i = 0; i < n; i++) {cache.put(i, new ArrayList<>());}for(int[] item: edges) {Integer first = item[0];Integer second = item[1];cache.get(first).add(second);cache.get(second).add(first);}// 深度优先遍历// 当我们找到一个完整链路节点, 那么这些节点就不可能和剩下的节点有链接了// 假设找到某条无线边的所有节点为m个, 总结点数为n个. 那么相互不能到达的两两节点数为 m * (n - m)boolean[] visited = new boolean[n];long result = 0;for(Integer key : cache.keySet()) {if(!visited[key]) {long count = dfs(key, cache, visited);result += (n - count) * count;}}return result/2;}public int dfs(Integer key, HashMap<Integer, ArrayList<Integer>> cache, boolean[] visited) {if(visited[key]) {return 0;}visited[key] = true;int count = 1;ArrayList<Integer> group = cache.get(key);for(Integer item : group) {if(visited[item] == false) {count += dfs(item, cache, visited);}}return count;} }复杂度分析:
- 时间复杂度: O(m + n), n 是总结点的个数, m是边数
- 空间复杂度: O(m + n)
结果如下所示.

相关文章:

2316. 统计无向图中无法互相到达点对数
2316. 统计无向图中无法互相到达点对数 难度: 中等 来源: 每日一题 2023.10.21 给你一个整数 n ,表示一张 无向图 中有 n 个节点,编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] [ai, bi] 表示节点 ai 和 bi 之间…...

Selenium定向爬取海量精美图片及搜索引擎杂谈
我自认为这是自己写过博客中一篇比较优秀的文章,同时也是在深夜凌晨2点满怀着激情和愉悦之心完成的。首先通过这篇文章,你能学到以下几点: 1.可以了解Python简单爬取图片的一些思路和方法 2.学习Selenium自动、测试分析动态网页和正则表达式的区别和共同点 …...
面试题—JAVA基础①
文章目录 1.Java面向对象有哪些特征?2.ArrayList和LinkedList有什么区别?3.Java接口和抽象类有哪些区别?4.hashcode和equals如何使用?5.try-catch6.局部变量和实例变量7.String、StringBuffer、StringBuilder 的区别?8…...

naive-ui的n-data-table标签奇特bug记录
具体参考之前的博文:vueday02——使用naive-ui做一个ACM看榜-CSDN博客 具体代码在这里面 原因:在本地运行的时候,datatable里面使用列表渲染成字符串前端设置样式进行转换,但是在正式部署的时候,这个组件没有将其自动…...

微信小程序OA会议系统个人中心授权登入
在我们的完成微信登入授权之前,首先我们要完成我们前面所写的代码,如果有不会的大家可以去看以下我发的前面几个文章链接我发下面了,各位加油! 微信小程序OA会议系统数据交互-CSDN博客 微信小程序会议OA系统其他页面-CSDN博客 …...
Git(一)Windows下安装及使用Git Bash
目录 一、简介1.1 什么是Git?1.2 Git 的主要特点1.3 什么是 Git Bash? 二、下载三、安装3.1 同意协议3.2 选择安装位置3.3 其他配置(【Next】 即可)3.4 安装完毕3.5 打开 Git Bash 官网地址: https://www.git-scm.com/…...
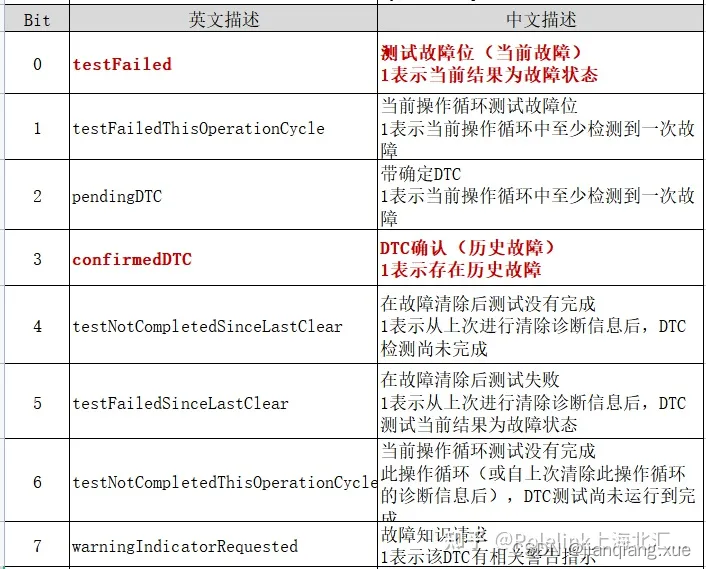
[AUTOSAR][诊断管理][ECU][$19] 读取ECU的DTC故障信息
一、简介 在车载诊断中常用的诊断协议有ISO 14229等,在协议中主要定义了诊断请求、诊断响应的报文格式及ECU该如何处理诊断请求的应用。其中ISO 14229系列标准协议定义了用于行业内诊断通信的需求规范,也就是UDS。UDS主要应用于OSI七层模型的第七层——…...
)
前端精度问题 (id 返回的和传给后端的不一致问题)
eg: 后端返回 id 10976458979374929 前端获取到的: 10976458979374928 原因: js 中 Number类型范围-2^53 1 到 2^53 - 1 Number.isSafeInteger()用来判断一个整数是否落在这个范围之内。 java中 Long 类型的取值范围是-2^63 1 到 2^63 - 1, 比JavaScript中大很多࿰…...
WPF Material Design UI框架
前言 Material Design in xaml 是开源免费的ui框架,工控软件主打的就是简单界面。 以下简称MD 相关资源 MaterialDesignInXamlToolkit Github 地址 MD 快速启动 MD 案例压缩包 MD 框架使用 启动环境配置 安装Nuget包 App.xaml 配置 <Application x:Class&qu…...
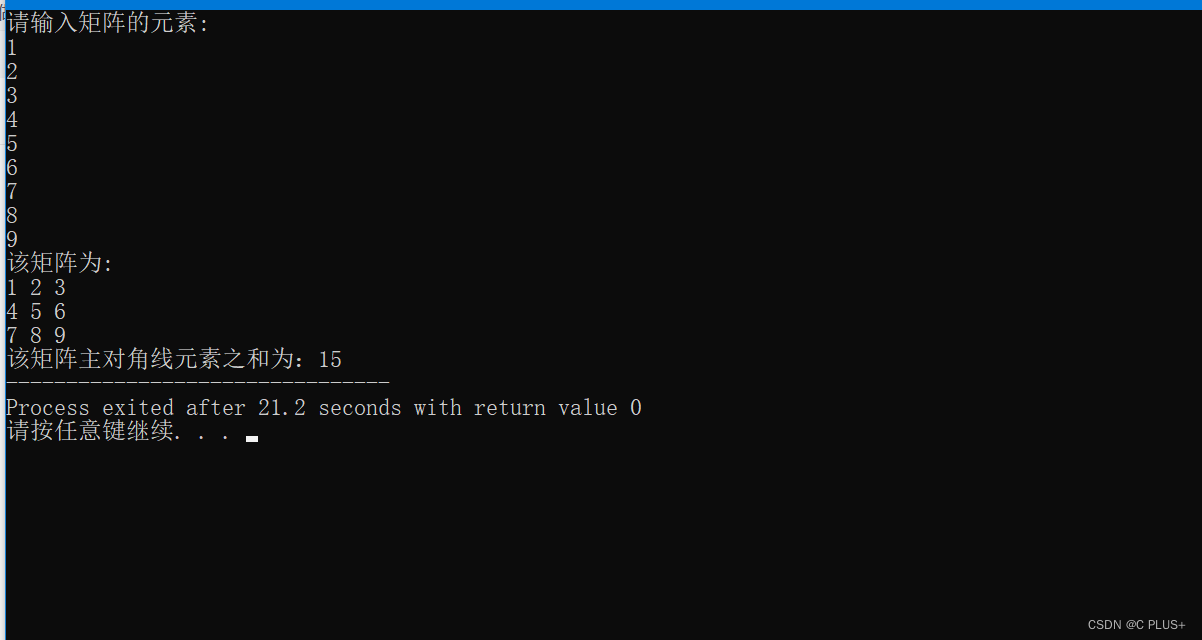
C语言求 3*3 矩阵对角线之和
完整代码: // 求 3*3 矩阵对角线之和 #include<stdio.h>int main() {int n3;int arr[3][3];// 输入矩阵printf("请输入矩阵的元素:\n");for (int i 0; i < n; i){for (int j 0; j < n; j){scanf("%d", &arr[i][j]);}}int su…...

缓存分片中的哈希算法与一致性哈希算法
什么是缓存分片 在高并发场景下,缓存往往成为了瓶颈。这时候,我们可以通过缓存数据分片的方式来解决问题。所谓缓存数据分片,就是将缓存数据按照一定的规则分成多个片段,每个片段由不同的缓存节点负责。这样做有两个好处…...
线框图软件:Balsamiq Wireframes mac中文介绍
Balsamiq Wireframes mac是一款用于创建线框图的软件工具。它旨在帮助用户快速制作出清晰、简洁的界面原型,以便在设计和开发过程中进行协作和沟通。 Balsamiq Wireframes具有简单直观的用户界面,使用户能够快速添加和编辑各种用户界面元素,如…...

【wxWidgets实现透明wxPanel_核心实现_原创思想】
描述 wxWidgets 根本就没有实现过透明wxPanel容器,你设置wxTRANSPARENT_WINDOW,结果sorry 黑色,哈哈哈哈, 就是和你作对.想想当下那么漂亮的桌面, 背景, 透明, 特效.哎 悲哀啊,实现不了,就那死板的界面特性. 网上找了好久,也是乱七八糟,改底层代码还是算了吧,升级特要命.都是只…...

重大技术问题,iPhone 15 Pro Max面临“烧屏门”风波 | 百能云芯
近期,社交媒体平台上陆续涌现大量用户和数码博主就iPhone 15 Pro Max出现烧屏问题的投诉与评论。 烧屏问题是OLED屏幕常见的一个缺陷,这是由OLED屏幕发光机制引发的,OLED屏幕可视为由无数微小的灯泡-像素点构成,这些像素点可以独立…...
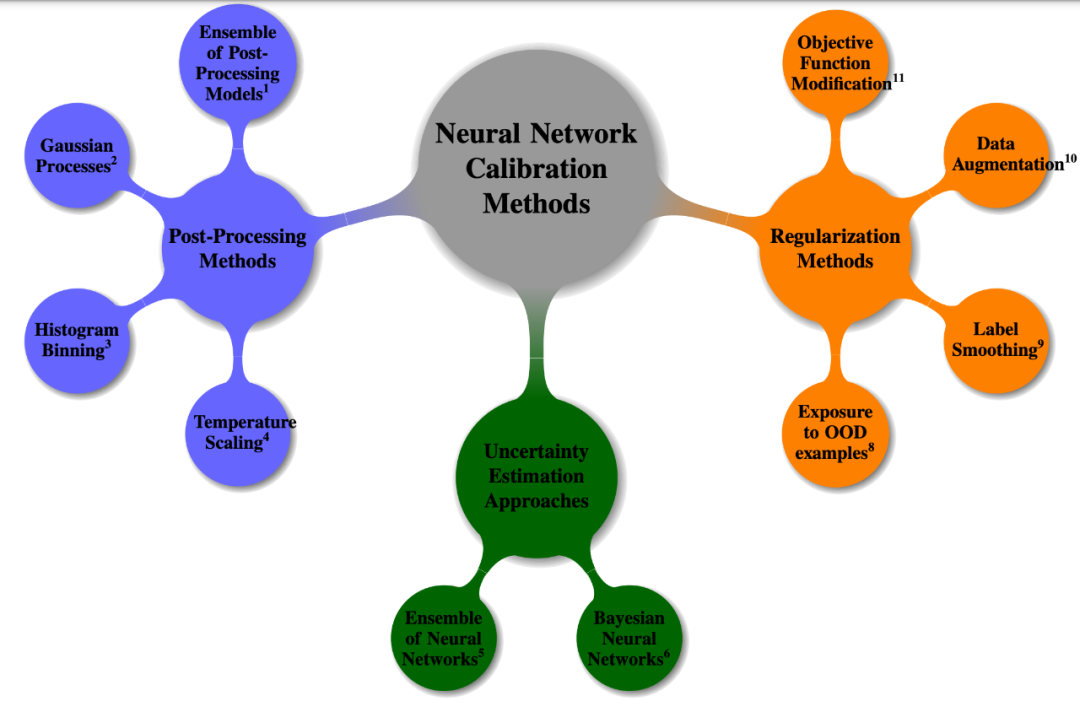
深度学习中的不确定性综述
领域学者: http://www.gatsby.ucl.ac.uk/~balaji/ 论文标题: A Survey of Uncertainty in Deep Neural Networks 论文链接: https://arxiv.org/pdf/2107.03342.pdf 概要 在过去的十年中,神经网络几乎遍及所有科学领域&#x…...

uni-app 小宠物 - 会说话的小鸟
在 template 中 <view class"container"><view class"external-shape"><view class"face-box"><view class"eye-box eye-left"><view class"eyeball-box eyeball-left"><span class"…...

POJ 3470 Walls 树上分桶
今天太晚了,代码先发上,思路明天说吧。 陌上花开,树上分桶 #include <iostream> #include <algorithm> #include <vector> using namespace std; /*** 对于y1不等于y2的,可以用datC求解,对于x1不等…...

HIVE-17824,删除hdfs分区信息,清理metastore元数据
当手动删除HDFS 分区数据时,但是并没有清理 Hive 中的分区元数据,删除操作无法自动更新hive分区表元数据。也就是从hdfs中删除大量分区数据,并没有执行如下命令: alter table drop partition commad 从hive 3.0.0开始可以使用MSCK的方法发现新分区或删除丢失的分区; MSCK [REPA…...
Python深度学习进阶与应用丨注意力(Attention)机制、Transformer模型、生成式模型、目标检测算法、图神经网络、强化学习详解等
目录 第一章 注意力(Attention)机制详解 第二章 Transformer模型详解 第三章 生成式模型详解 第四章 目标检测算法详解 第五章 图神经网络详解 第六章 强化学习详解 第七章 深度学习模型可解释性与可视化方法详解 更多应用 近年来,伴…...
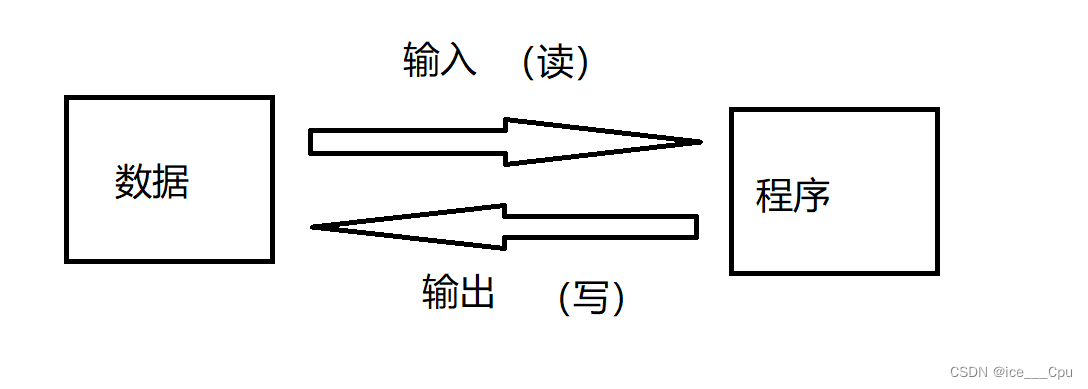
javaEE -6(10000详解文件操作)
一:认识文件 我们先来认识狭义上的文件(file)。针对硬盘这种持久化存储的I/O设备,当我们想要进行数据保存时,往往不是保存成一个整体,而是独立成一个个的单位进行保存,这个独立的单位就被抽象成文件的概念,…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

LeetCode 0386.字典序排数:细心总结条件
【LetMeFly】386.字典序排数:细心总结条件 力扣题目链接:https://leetcode.cn/problems/lexicographical-numbers/ 给你一个整数 n ,按字典序返回范围 [1, n] 内所有整数。 你必须设计一个时间复杂度为 O(n) 且使用 O(1) 额外空间的算法。…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...
