C++动态规划算法的应用:得到 K 个半回文串的最少修改次数 原理源码测试用例
本文涉及的基础知识点
动态规划
题目
得到 K 个半回文串的最少修改次数
给你一个字符串 s 和一个整数 k ,请你将 s 分成 k 个 子字符串 ,使得每个 子字符串 变成 半回文串 需要修改的字符数目最少。
请你返回一个整数,表示需要修改的 最少 字符数目。
注意:
如果一个字符串从左往右和从右往左读是一样的,那么它是一个 回文串 。
如果长度为 len 的字符串存在一个满足 1 <= d < len 的正整数 d ,len % d == 0 成立且所有对 d 做除法余数相同的下标对应的字符连起来得到的字符串都是 回文串 ,那么我们说这个字符串是 半回文串 。比方说 “aa” ,“aba” ,“adbgad” 和 “abab” 都是 半回文串 ,而 “a” ,“ab” 和 “abca” 不是。
子字符串 指的是一个字符串中一段连续的字符序列。
示例 1:
输入:s = “abcac”, k = 2
输出:1
解释:我们可以将 s 分成子字符串 “ab” 和 “cac” 。子字符串 “cac” 已经是半回文串。如果我们将 “ab” 变成 “aa” ,它也会变成一个 d = 1 的半回文串。
该方案是将 s 分成 2 个子字符串的前提下,得到 2 个半回文子字符串需要的最少修改次数。所以答案为 1 。
示例 2:
输入:s = “abcdef”, k = 2
输出:2
解释:我们可以将 s 分成子字符串 “abc” 和 “def” 。子字符串 “abc” 和 “def” 都需要修改一个字符得到半回文串,所以我们总共需要 2 次字符修改使所有子字符串变成半回文串。
该方案是将 s 分成 2 个子字符串的前提下,得到 2 个半回文子字符串需要的最少修改次数。所以答案为 2 。
示例 3:
输入:s = “aabbaa”, k = 3
输出:0
解释:我们可以将 s 分成子字符串 “aa” ,“bb” 和 “aa” 。
字符串 “aa” 和 “bb” 都已经是半回文串了。所以答案为 0 。
参数范围:
2 <= s.length <= 200
1 <= k <= s.length / 2
s 只包含小写英文字母。
分析
第一轮:vector<vector> m_aDCenger[2][101]; 四维数组:第一维,0表示奇数长度,1表示偶数长度。 第二维:d。第三维:中心。第四维半长长度。值记录变成:半回文需要改变的次数。
第二轮:int m_vNeedNum[200][201] 记录s[left,r)变成半回文需要改变的次数。
第三轮:三层循环,第一层循环:枚举k,第二层循环枚举s[0,j]。第三轮循环枚举m,[0,m]和(m,j]。
三轮时间复杂度都是:O(nnn);
核心代码
class Solution {
public:
int minimumChanges(string s, int k) {
m_c = s.length();
Init(s);
Init2(s);
vector pre(m_c);//pre[j]将s[0,j]拆分成i-1个子字符串,这些子串全部半回文的需要改变的字符数
for (int j = 0; j < m_c; j++)
{
pre[j] = m_vNeedNum[0][j + 1];
}
for (int i = 2; i <= k; i++)
{
vector dp(m_c);
for (int j = i - 1; j < m_c; j++)
{//拆分成[0,m]和(m,j]([m+1,j+1)),前者i-1个子串,后者一个子串
int iMin = INT_MAX;
for (int m = max(0,i-2); m < j; m++)
{
const int cur = pre[m] + m_vNeedNum[m + 1][j + 1];
iMin = min(iMin, cur);
}
dp[j] = iMin;
}
pre.swap(dp);
}
return pre.back();
}
void Init(std::string& s)
{
for(int i = 0 ; i < 2 ; i++ )
for (int j = 0; j <= m_c / 2; j++)
{
m_aDCenger[i][j].assign(m_c+1, vector((m_c+1)/2+1));
}
for (int d = 1; d <= m_c/2; d++)
{
for (int center = 0; center < m_c; center++)
{
int halfLen = 1;
while ((center + d* (halfLen-1) < m_c) && (center - d* (halfLen - 1) >= 0) )
{
m_aDCenger[1][d][center][halfLen] = m_aDCenger[1][d][center][halfLen - 1] +(s[center + d * (halfLen - 1)] != s[center - d * (halfLen - 1)]) ;
halfLen++;
}
}
for (int center = 0; center < m_c; center++)
{//偶数半回文
int halfLen = 1;
while ((center + d * halfLen < m_c) && (center - d * (halfLen - 1) >= 0) )
{
m_aDCenger[0][d][center][halfLen] = m_aDCenger[0][d][center][halfLen - 1] + (s[center + d * halfLen] != s[center - d * (halfLen - 1)]);
halfLen++;
}
}
}
}
void Init2(std::string& s)
{
memset(m_vNeedNum, sizeof(m_vNeedNum), 0);
for (int left = 0; left < m_c; left++)
{
for (int r = left + 1; r <= m_c; r++)
{
const int subLen = r - left;
int iNeed = 1000*1000;
for (int d = 1; (d * d <= subLen)&&(subLen >1); d++)
{
if (0 != subLen % d)
{
continue;
}
{
const int iCurNeed = DoLeftRightD(left, r, d);
iNeed = min(iNeed, iCurNeed);
}
if(d >1 )
{
const int iCurNeed = DoLeftRightD(left, r, subLen/d);
iNeed = min(iNeed, iCurNeed);
}
}
m_vNeedNum[left][r] = iNeed;
}
}
}
int DoLeftRightD(int left,int r,int d)
{
const int subLen = r - left;
const int len = subLen / d;
const auto& arr = m_aDCenger[len % 2];
const int midIndex = (len-1)/2;
int iCurNeed = 0;
for (int begin = 0; begin < d; begin++)
{
const int center = left + begin + midIndex * d;
iCurNeed += arr[d][center][(len + 1) / 2];
}
return iCurNeed;
}
int m_c;
vector<vector> m_aDCenger[2][101];
int m_vNeedNum[200][201];
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
//string s = “bbacccbbaabbddddddddddddddddddddddddddddddddddddddddddddbbacccbbaabbdddddddddddddddddddddddddddddddddddddddddddddbbbacccbbaabbddddddddddddddddddddbbacccbbaabbdddddddddddddddddddddddddddddddddddddddddd”;
string s = “abcac”;
int k = 2;
Solution slu;
auto res = slu.minimumChanges(s,k);
Assert(1, res);
//CConsole::Out(res);
}
小幅改进
空间复杂度降为O(nn)。一,预处理的时候,利用当前d,更新m_vLeftRightToNeedChange。更新完旧d的信息就不需要了。二,不需要分奇数长度和偶数长度回文。长度本身可以分奇偶了。
Init2共3层循环,时间复杂度是:O(nn),第三层第四层,时间复杂度共O(n)。第三层循环的时间复杂度是: n/d,第四层时间复杂度是d。
新代码
class Solution {
public:int minimumChanges(string s, int k) {m_c = s.length(); m_vLeftRightToNeedChange.assign(m_c, vector<int>(m_c, m_iNotMay));for (int d = 1; d <= m_c / 2; d++){Init(s,d);Init2(s,d);}vector<int> pre(m_c);//pre[j]将s[0,j]拆分成i-1个子字符串,这些子串全部半回文的需要改变的字符数for (int j = 0; j < m_c; j++){pre[j] = m_vLeftRightToNeedChange[0][j];}for (int i = 2; i <= k; i++){vector<int> dp(m_c);for (int j = i - 1; j < m_c; j++){//拆分成[0,m]和(m,j]([m+1,j])),前者i-1个子串,后者一个子串int iMin = INT_MAX;for (int m = max(0,i-2); m < j; m++){const int cur = pre[m] + m_vLeftRightToNeedChange[m + 1][j];iMin = min(iMin, cur);}dp[j] = iMin;}pre.swap(dp);}return pre.back();}void DoCenter(int center, bool bEven,int d,const string& s){int left = center, r = left + d*bEven;if (r >= m_c){return;}m_vDLeftRightToNeedChange[left][r] = (s[left] != s[r]);left -= d;r += d;while ((r < m_c) && (left >= 0 )){m_vDLeftRightToNeedChange[left][r] = m_vDLeftRightToNeedChange[left + d][r - d] + (s[left] != s[r]);left -= d;r += d;}}void Init(std::string& s,int d ){m_vDLeftRightToNeedChange.assign(m_c, vector<int>(m_c, m_iNotMay)); for (int center = 0; center < m_c; center++){DoCenter(center, true, d,s);DoCenter(center, false, d,s);}}void Init2(std::string& s, int d){ for (int left = 0; left < m_c; left++){for (int iSubLen = 2; left+ iSubLen*d <= m_c ; iSubLen++){const int r = left + iSubLen * d;int iNeedChange = 0;for (int j = 0; j < d; j++){iNeedChange += m_vDLeftRightToNeedChange[left+j][r - d+j];}m_vLeftRightToNeedChange[left][r - 1] = min(m_vLeftRightToNeedChange[left][r - 1],iNeedChange);}}} const int m_iNotMay = 1000 * 1000;int m_c;vector<vector<int>> m_vDLeftRightToNeedChange;//m_vDLeftRightToNeedChange[left][r],表示当前d,str[left,left+d....r]是回文的最少次数vector<vector<int>> m_vLeftRightToNeedChange;//m_vLeftRightToNeedChange[left][r]表示s[left,r]变成半回文的最少改变次数
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 鄙人想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17

相关文章:

C++动态规划算法的应用:得到 K 个半回文串的最少修改次数 原理源码测试用例
本文涉及的基础知识点 动态规划 题目 得到 K 个半回文串的最少修改次数 给你一个字符串 s 和一个整数 k ,请你将 s 分成 k 个 子字符串 ,使得每个 子字符串 变成 半回文串 需要修改的字符数目最少。 请你返回一个整数,表示需要修改的 最少…...
Pyside6 QFileDialog
Pyside6 QFileDialog Pyside6 QFileDialog常用函数getOpenFileNamegetOpenFileNamesgetExistingDirectorygetSaveFileName 程序界面程序主程序 Pyside6 QFileDialog提供了一个允许用户选择文件或目录的对话框。关于QFileDialog的使用可以参考下面的文档 https://doc.qt.io/qtfo…...

Leetcode1793. Maximum Score of a Good Subarray
给定一个数组和一个下标 k k k 子数组 ( i , j ) (i,j) (i,j)分数定义为 min ( n u m s [ i ] , n u m s [ i 1 ] , ⋯ , n u m s [ j ] ) ∗ ( j − i 1 ) \min\left(nums[i], nums[i 1],\cdots, nums[j]\right)*\left(j-i1\right) min(nums[i],nums[i1],⋯,nums[j])∗(…...
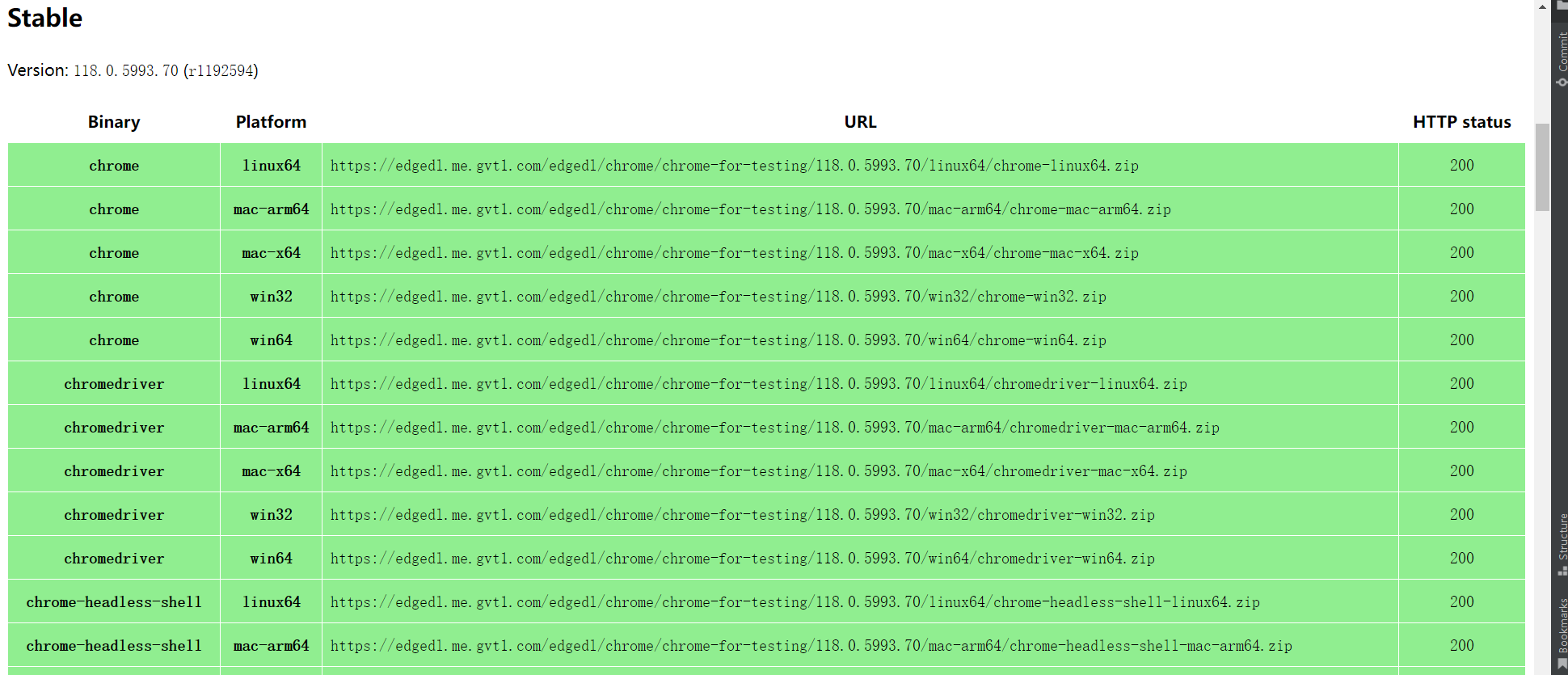
只需五步,在Linux安装chrome及chromedriver(CentOS)
一、安装Chrome 1)先执行命令下载chrome: wget https://dl.google.com/linux/direct/google-chrome-stable_current_x86_64.rpm2)安装chrome yum localinstall google-chrome-stable_current_x86_64.rpm看到下图中的Complete出现则代表安装…...
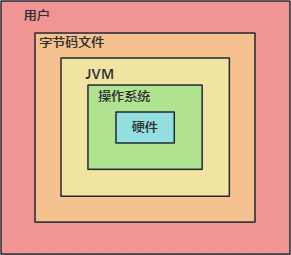
第01章-Java语言概述
目录 1 常见DOS命令 常用指令 相对路径与绝对路径 2 转义字符 3 安装JDK与配置环境变量 JDK与JRE JDK的版本 JDK的下载 JDK的安装 配置path环境变量 4 Java程序的编写与执行 5 Java注释 6 Java API文档 7 Java核心机制:JVM 1 常见DOS命令 DOS(…...

Spring | Spring Cache 缓存框架
Spring Cache 缓存框架: Spring Cache功能介绍Spring Cache的Maven依赖Spring Cache的常用注解EnableCaching注解CachePut注解Cacheable注解CacheEvict注解 Spring Cache功能介绍 Spring Cache是Spring的一个框架,实现了基于注解的缓存功能。只需简单加一…...
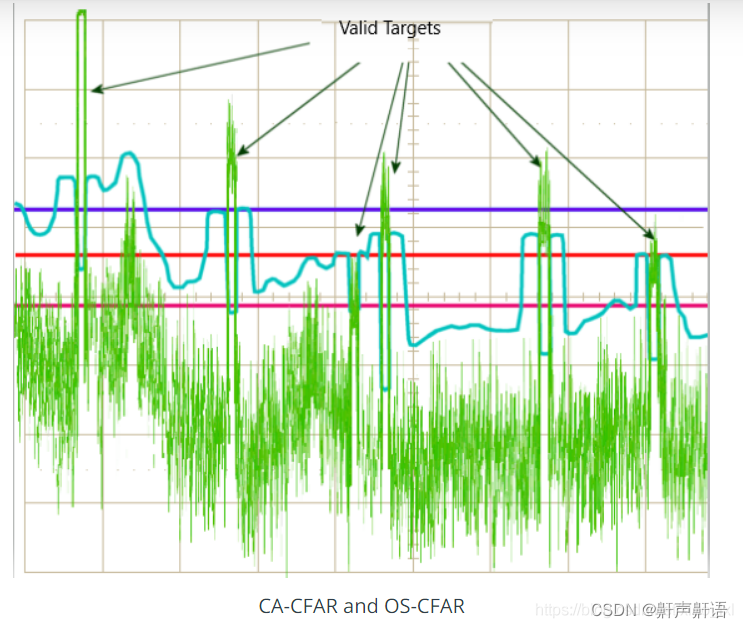
雷达开发的基本概念fft,cfar,以及Clutter, CFAR,AoA
CFAR Constant False-Alarm Rate的缩写。在雷达信号检测中,当外界干扰强度变化时,雷达能自动调整其灵敏度,使雷达的虚警概率保持不变。具有这种特性的接收机称为恒虚警接收机。雷达信号的检测总是在干扰背景下进行的,这些干扰包括…...

什么是大数据测试?有哪些类型?应该怎么测?
随着目前世界上各个国家使用大数据应用程序或应用大数据技术场景的数量呈指数增长,相应的,对于测试大数据应用时所需的知识与大数据测试工程师的需求也在同步增加。 针对大数据测试的相关技术已慢慢成为当下软件测试人员需要了解和掌握的一门通用技术。…...

03-垃圾收集策略与算法
垃圾收集策略与算法 程序计数器、虚拟机栈、本地方法栈随线程而生,也随线程而灭;栈帧随着方法的开始而入栈,随着方法的结束而出栈。这几个区域的内存分配和回收都具有确定性,在这几个区域内不需要过多考虑回收的问题,因…...

1.AUTOSAR的架构及方法论
在15、16年之前,AUTOSAR这个东西其实是被国内很多大的OEM或者供应商所排斥的。为什么?最主要的原因还是以前采用手写底层代码+应用层模型生成代码的方式进行开发。每个供应商或者OEM都有自己的软件规范或者技术壁垒,现在提个AUTOSAR想搞统一,用一个规范来收割汽车软件供应链…...

Kotlin中的List集合
在Kotlin中,List集合用于存储一组有序的元素。List集合分为可变集合(MutableList)和不可变集合(List)。本篇博客将分别介绍可变集合和不可变集合,并提供相关的API示例代码。 不可变集合(List&a…...

微信小程序WeUI项目weui-miniprogram如何运行起来?
微信小程序WeUI项目weui-miniprogram如何运行起来? 解决方法: 1、下载 https://github.com/wechat-miniprogram/weui-miniprogram 2、在项目根目录weui-miniprogram-master执行以下命令安装依赖: npm install 3、继续执行编译命令: npm r…...
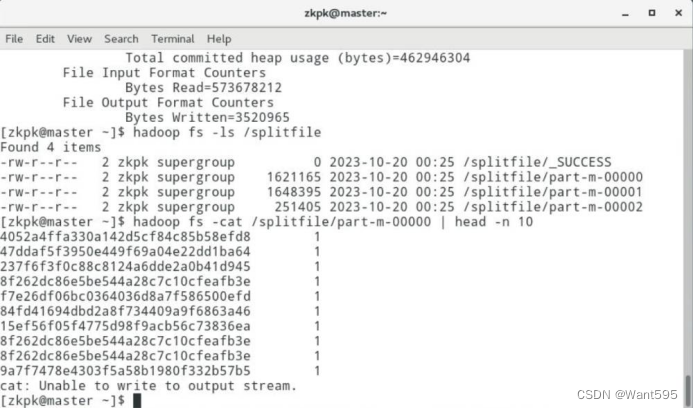
MapReduce编程:检索特定群体搜索记录和定义分片操作
文章目录 MapReduce 编程:检索特定群体搜索记录和定义分片操作一、实验目标二、实验要求及注意事项三、实验内容及步骤 附:系列文章 MapReduce 编程:检索特定群体搜索记录和定义分片操作 一、实验目标 熟悉MapReduce编程涉及的主要类和接口…...
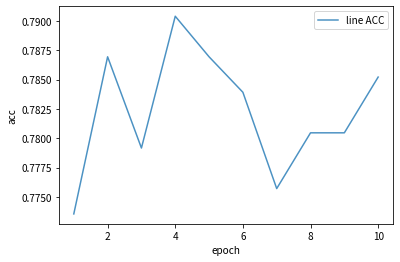
pytorch 入门 (四)案例二:人脸表情识别-VGG16实现
实战教案二:人脸表情识别-VGG16实现 本文为🔗小白入门Pytorch内部限免文章 参考本文所写记录性文章,请在文章开头注明以下内容,复制粘贴即可 🍨 本文为🔗小白入门Pytorch中的学习记录博客🍦 参…...

数据结构--线性表回顾
目录 线性表 1.定义 2.线性表的基本操作 3.顺序表的定义 3.1顺序表的实现--静态分配 3.2顺序表的实现--动态分配 4顺序表的插入、删除 4.1插入操作的时间复杂度 4.2顺序表的删除操作-时间复杂度 5 顺序表的查找 5.1按位查找 5.2 动态分配的方式 5.3按位查找的时间…...
ChatGPT(1):ChatGPT初识
1 ChatGPT原理 ChatGPT 是基于 GPT-3.5 架构的一个大型语言模型,它的工作原理涵盖了深度学习和自然语言处理技术。以下是 ChatGPT 的工作原理的一些关键要点: 神经网络架构:ChatGPT 的核心是一个深度神经网络,采用了变种的 Tran…...

PostgreSQL 插件 CREATE EXTENSION 原理
PostgreSQL 提供了丰富的数据库内核编程接口,允许开发者在不修改任何 Postgres 核心代码的情况下以插件的形式将自己的代码融入内核,扩展数据库功能。本文探究了 PostgreSQL 插件的一般源码组成,梳理插件的源码内容和实现方式;并介…...

Android常见分区
一、Google官方标准分区 1. Boot分区 包含Linux内核和一个最小的root文件系统(装载到ramdisk中),用于挂载系统和其他的分区并开始Runtime。正如名字所代表的意思(注:boot的意思是启动),这个分区使Android设备可以启动…...

华为鸿蒙4谷歌GMS安装教学
目录 问题描述 参考视频 教学视频1 配套文档 教学视频2 资源包(配套视频1) 设备未经 play 保护机制认证 问题描述 很多国外的最新应用需要再Google商店才能下载比如ChatGPT 华为手机不支持 Google Play 服务的原因主要是由于谷歌服务框架(GMS)未…...
原型设计工具:Balsamiq Wireframes 4.7.4 Crack
原型设计工具:Balsamiq Wireframes是一种快速的低保真UI 线框图工具,可重现在记事本或白板上绘制草图但使用计算机的体验。 它确实迫使您专注于结构和内容,避免在此过程后期对颜色和细节进行冗长的讨论。 线框速度很快:您将产生更多想法&am…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
