Kotlin中的List集合
在Kotlin中,List集合用于存储一组有序的元素。List集合分为可变集合(MutableList)和不可变集合(List)。本篇博客将分别介绍可变集合和不可变集合,并提供相关的API示例代码。
不可变集合(List)
不可变集合是指在创建后其内容不可更改的集合。在Kotlin中,我们可以使用listOf函数来创建不可变集合。以下是对不可变集合的一些常用操作:
// 创建空的不可变集合
val mList: List<Int> = listOf()// 创建包含元素的不可变集合
val mList1: List<Int> = listOf(1, 2, 3)
val mList2: List<Int> = listOf(1, 2, 3, 4, 5, 3)// 判断集合是否为空
if (mList2.isEmpty()) {println("集合中没有元素")
} else {// 获取集合中的元素个数println("集合中的元素个数为:${mList2.size}")
}// 是否包含一个元素
if (mList2.contains(1)) {println("集合中包含元素1")
}// 是否包含多个元素
if (mList2.containsAll(mList1)) {println("集合中包含元素" + mList1)
}// 遍历集合中的所有元素
for (element in mList2) {print("$element\t") // 输出:1 2 3 4 5 3
}
println()// 检索元素
println("集合中索引为0的元素是:${mList2.get(0)}") // 输出:集合中索引为0的元素是:1
println("元素3第一次出现的位置:${mList2.indexOf(3)}") // 输出:元素3第一次出现的位置:2
println("元素3最后出现的位置:${mList2.lastIndexOf(3)}") // 输出:元素3最后出现的位置:5
println("截取集合中索引为1-4的元素:${mList2.subList(1, 4)}") // 输出:截取集合中索引为1-4的元素:[2, 3, 4]
在上述代码中,我们首先通过listOf函数创建了不可变集合mList2,然后对其进行了一系列操作。我们可以判断集合是否为空,获取集合的大小,判断集合是否包含某个元素,遍历集合中的所有元素,检索元素的位置以及截取集合的子集。
可变集合(MutableList)
可变集合是指在创建后可以修改其内容的集合。在Kotlin中,我们可以使用mutableListOf函数来创建可变集合。除了不可变集合支持的操作外,可变集合还可以进行添加、插入、移除和修改操作。以下是对可变集合的一些常用操作:
// 创建可变集合
var muList: MutableList<Int> = mutableListOf(1, 2, 3)// 添加一个元素
muList.add(6) // [1, 2, 3, 6]// 插入一个元素
muList.add(1, 5) // [1, 5, 2, 3, 6]// 移除一个元素(按值)
muList.remove(1) // [5, 2, 3, 6]// 移除一个元素(按索引)
muList.removeAt(0) // [2, 3, 6]// 修改元素
muList.set(0, 99) // [99, 3, 6]println(muList) // 输出:[99, 3, 6]// 清空集合
muList.clear()
println(muList) // 输出:[]
在上述代码中,我们首先通过mutableListOf函数创建了可变集合muList,然后对其进行了一系列操作。我们可以添加元素到可变集合中,插入元素到指定位置,移除元素(按值或按索引),修改元素的值,以及清空集合。
总结:
- 不可变集合(List)是指创建后内容不可更改的集合,使用
listOf函数创建。 - 可变集合(MutableList)是指创建后可以修改内容的集合,使用
mutableListOf函数创建。 - 不可变集合和可变集合都支持常用的集合操作,如判断是否为空、获取元素个数、检索元素位置等。
- 可变集合还支持添加、插入、移除和修改元素的操作。
通过合理地选择不可变集合和可变集合,我们可以在Kotlin中高效地管理和操作集合数据。
相关文章:

Kotlin中的List集合
在Kotlin中,List集合用于存储一组有序的元素。List集合分为可变集合(MutableList)和不可变集合(List)。本篇博客将分别介绍可变集合和不可变集合,并提供相关的API示例代码。 不可变集合(List&a…...

微信小程序WeUI项目weui-miniprogram如何运行起来?
微信小程序WeUI项目weui-miniprogram如何运行起来? 解决方法: 1、下载 https://github.com/wechat-miniprogram/weui-miniprogram 2、在项目根目录weui-miniprogram-master执行以下命令安装依赖: npm install 3、继续执行编译命令: npm r…...
MapReduce编程:检索特定群体搜索记录和定义分片操作
文章目录 MapReduce 编程:检索特定群体搜索记录和定义分片操作一、实验目标二、实验要求及注意事项三、实验内容及步骤 附:系列文章 MapReduce 编程:检索特定群体搜索记录和定义分片操作 一、实验目标 熟悉MapReduce编程涉及的主要类和接口…...
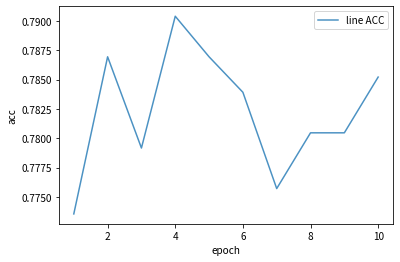
pytorch 入门 (四)案例二:人脸表情识别-VGG16实现
实战教案二:人脸表情识别-VGG16实现 本文为🔗小白入门Pytorch内部限免文章 参考本文所写记录性文章,请在文章开头注明以下内容,复制粘贴即可 🍨 本文为🔗小白入门Pytorch中的学习记录博客🍦 参…...

数据结构--线性表回顾
目录 线性表 1.定义 2.线性表的基本操作 3.顺序表的定义 3.1顺序表的实现--静态分配 3.2顺序表的实现--动态分配 4顺序表的插入、删除 4.1插入操作的时间复杂度 4.2顺序表的删除操作-时间复杂度 5 顺序表的查找 5.1按位查找 5.2 动态分配的方式 5.3按位查找的时间…...
ChatGPT(1):ChatGPT初识
1 ChatGPT原理 ChatGPT 是基于 GPT-3.5 架构的一个大型语言模型,它的工作原理涵盖了深度学习和自然语言处理技术。以下是 ChatGPT 的工作原理的一些关键要点: 神经网络架构:ChatGPT 的核心是一个深度神经网络,采用了变种的 Tran…...

PostgreSQL 插件 CREATE EXTENSION 原理
PostgreSQL 提供了丰富的数据库内核编程接口,允许开发者在不修改任何 Postgres 核心代码的情况下以插件的形式将自己的代码融入内核,扩展数据库功能。本文探究了 PostgreSQL 插件的一般源码组成,梳理插件的源码内容和实现方式;并介…...

Android常见分区
一、Google官方标准分区 1. Boot分区 包含Linux内核和一个最小的root文件系统(装载到ramdisk中),用于挂载系统和其他的分区并开始Runtime。正如名字所代表的意思(注:boot的意思是启动),这个分区使Android设备可以启动…...

华为鸿蒙4谷歌GMS安装教学
目录 问题描述 参考视频 教学视频1 配套文档 教学视频2 资源包(配套视频1) 设备未经 play 保护机制认证 问题描述 很多国外的最新应用需要再Google商店才能下载比如ChatGPT 华为手机不支持 Google Play 服务的原因主要是由于谷歌服务框架(GMS)未…...
原型设计工具:Balsamiq Wireframes 4.7.4 Crack
原型设计工具:Balsamiq Wireframes是一种快速的低保真UI 线框图工具,可重现在记事本或白板上绘制草图但使用计算机的体验。 它确实迫使您专注于结构和内容,避免在此过程后期对颜色和细节进行冗长的讨论。 线框速度很快:您将产生更多想法&am…...
Nginx Proxy代理
代理原理 反向代理产生的背景: 在计算机世界里,由于单个服务器的处理客户端(用户)请求能力有一个极限,当用户的接入请求蜂拥而入时,会造成服务器忙不过来的局面,可以使用多个服务器来共同分担成…...
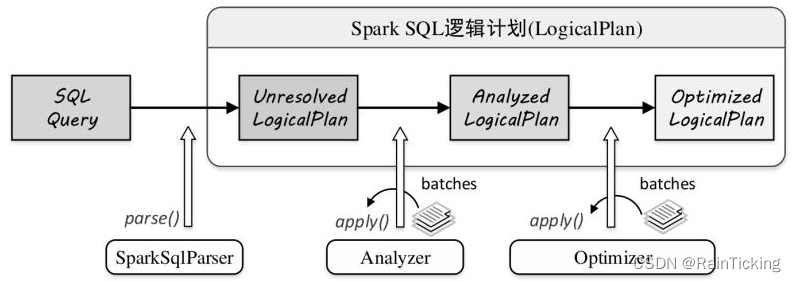
SparkSQL之LogicalPlan概述
逻辑计划阶段在整个流程中起着承前启后的作用。在此阶段,字符串形态的SQL语句转换为树结构形态的逻辑算子树,SQL中所包含的各种处理逻辑(过滤、剪裁等)和数据信息都会被整合在逻辑算子树的不同节点中。逻辑计划本质上是一种中间过…...

Ubuntu 安装 kubectl、kubeadm 和 kubelet
你需要在每台机器上安装以下的软件包: kubeadm:用来初始化集群的指令。 kubelet:在集群中的每个节点上用来启动 Pod 和容器等。 kubectl:用来与集群通信的命令行工具。 kubeadm 不能帮你安装或者管理 kubelet 或 kubectl&#…...

C语言获取文件长度
C语言获取文件长度 文章目录 C语言获取文件长度一、使用标准库方法二、使用Linux系统调用 一、使用标准库方法 #include <stdio.h>long get_file_size(const char * filename ){long size 0;FILE * fp fopen(filename,"rb");if( fp NULL ) {printf("o…...

【面试经典150 | 哈希表】快乐数
文章目录 写在前面Tag题目来源题目解读解题思路方法一:哈希集合判重方法二:快慢指针判重 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为…...
ETL实现实时文件监听
一、实时文件监听的作用及应用场景 实时文件监听是一种监测指定目录下的文件变化的技术,当产生新文件或者文件被修改时,可实时提醒用户并进行相应处理。这种技术广泛应用于数据备份、日志管理、文件同步和版本控制等场景,它可以帮助用户及时…...
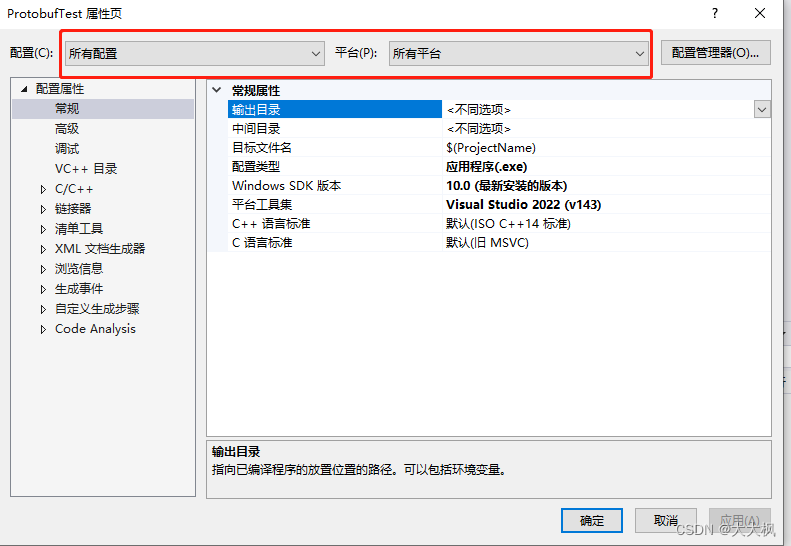
Openssl数据安全传输平台003:Protobuf - 部署
文章目录 Github代码仓库位置一、Windows环境配置生成库文件之后—>参考3.3 配置VS1. 先将平台设置为所有平台2. 配置属性 >> C/C >> 常规 >> 附加包含目录3. 配置属性 >> C/C >> 预处理器 >> 预处理器定义,添加4. 配置属性 >> C…...
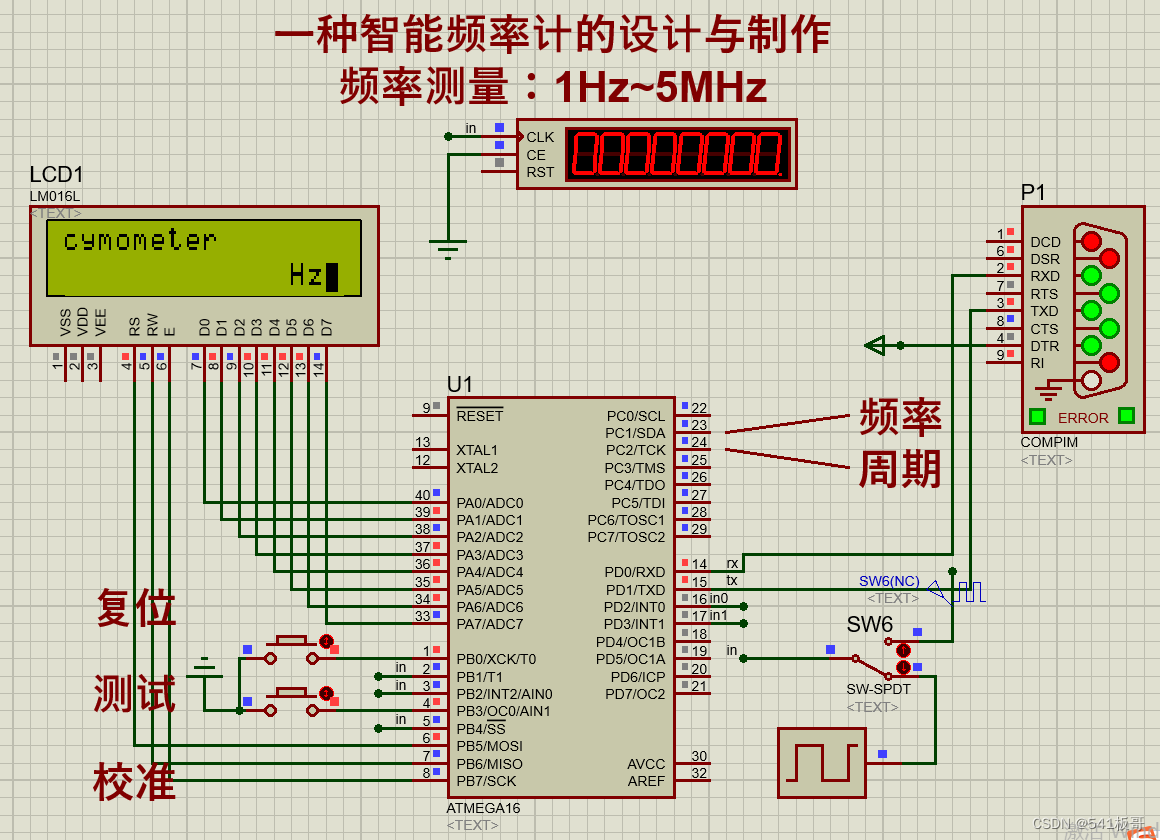
Proteus仿真--一种智能频率计的设计与制作(AVR单片机+proteus仿真)
本文介绍一种基于AVR单片机实现的一种智能频率计Proteus仿真实现(完整仿真源文件及代码见文末链接) 简介 硬件电路主要分为单片机主控模块、频率计模块、LCD1602液晶显示模块以及串口模块 (1)单片机主控模块:单片机…...
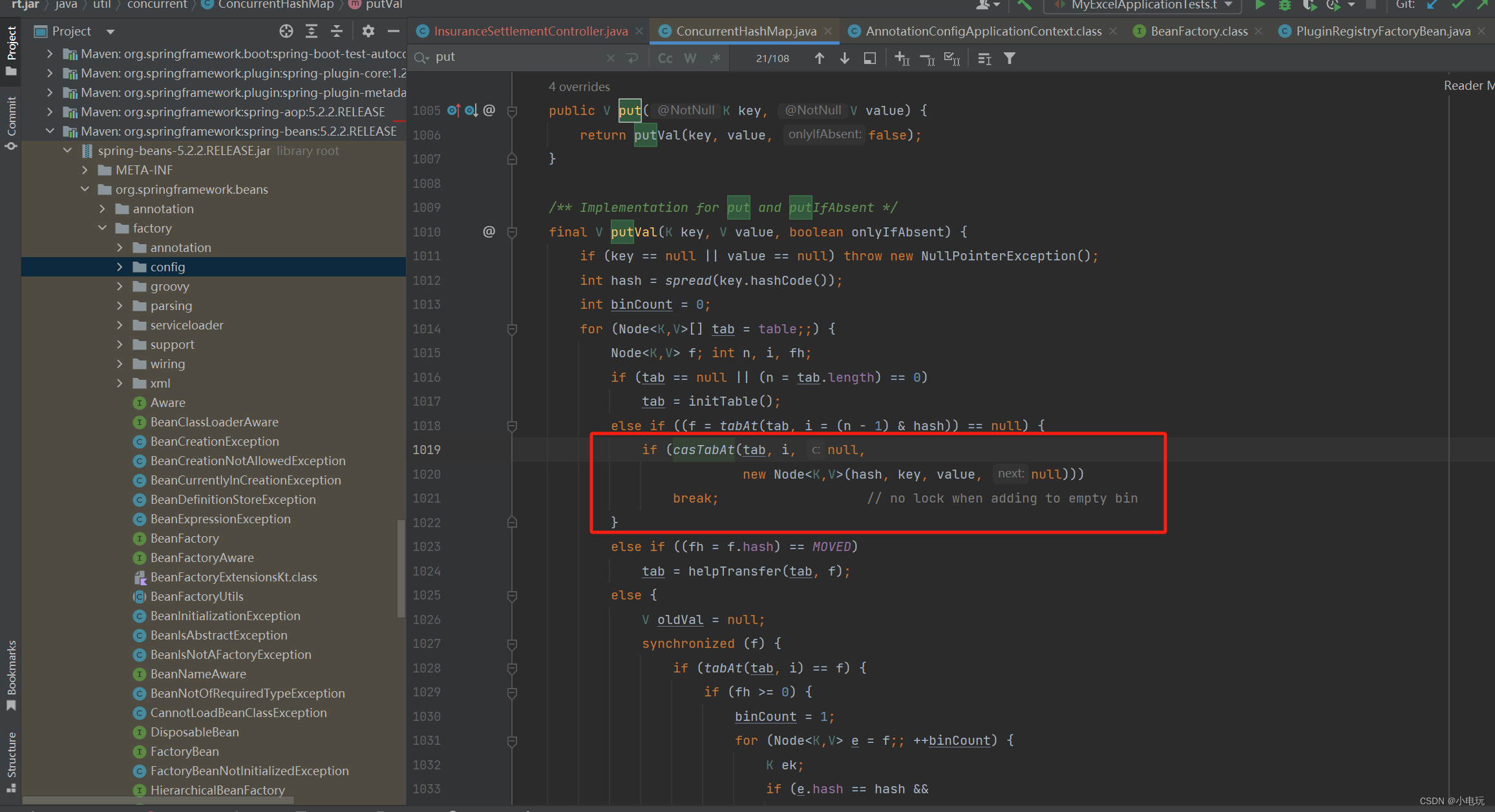
CAS是“Compare and Swap“(比较并交换)
CAS是"Compare and Swap"(比较并交换) 一,介绍 CAS是"Compare and Swap"(比较并交换)的缩写,是一种多线程同步的原子操作。它基于硬件的原子性保证,用于解决并发环境下的…...

前端数据可视化之【series、series饼图配置】配置项
目录 🌟Echarts配置项🌟series🌟饼图 type:pie🌟写在最后 🌟Echarts配置项 ECharts开源来自百度商业前端数据可视化团队,基于html5 Canvas,是一个纯Javascript图表库,提供直观&…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...
