【LeetCode 704】【Go】二分查找
二分查找题解
一、碎碎念
从本周开始,重新更新刷题记录了哈。
基于费曼学习法的原理,最好的输入是输出,所以与大家分享。
鉴于目前这个糟糕的市场环境,还是要练好自己的基本技术,万一那天就被迫 N + 1了,你说是吧。
Leetcode 两年没见,出了个分块刷题的区域。甚好,就照着这个边刷边给各位分享吧。
二、正文
1. 简介
二分算法是一个比较常用的基础算法。
本期分享的是两道简单题,重点在于解析二分算法的原理和注意点,而不在于难度。
2.算法原理
二分算法的原理很简单,顾名思义。
是将一组有序数据从中间二分,循环比较中值,根据中值和目标值的比较来决定最右边左移还是最左边右移后进入下一个循环,或者满足退出条件后退出循环。
好,那么开始提炼关键点。
首先,得是有序数据,只有有序,中值的比较才有意义。不然中值的左右两边都比中值大或者小。鬼知道移动最左边还是最右边。
二,要根据中值和目标值的比较来确定是否进入下一个循环或者退出。也就是确定退出条件。这个就要看清楚题干中的条件了。诸如升序降序,和目标值相等还是小于某个值的最下值
最后,还有几个注意点在代码分析时讲解。
3.代码实操
题目 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
func search(nums []int, target int) int {l, r, m, num := 0, len(nums)-1, 0, 0for l <= r {m = (r - l)/2 + lnum = nums[m]if num == target {return m} else if num > target {r = m - 1} else {l = m + 1}}return -1
}
代码不复杂,仔细研究下,凭借各位的聪明才智肯定能读懂。但有几个隐藏的注意点需要关注。
首先,循环遍历时,最左边要小于等于右边。这个等于很关键,因为二分分到非整值时是自动取小的数的。有可能遍历到最后就俩值。先遍历到了小的,但目标是大值,等你右移的话,假如没等于号,那你就退出循环了,没找到目标值报错咯。
然后,要注意中值的取法。应该是最右边减最左边的一半加上最左边。因为起点不是 0,而是最左边。你要找的是最左边与最右边的中值。
最后,移动边界时。不必取中值本身。这个倒是取决于题干的,本题不取是因为找等于目标值的对象。中值没取到就可以被过滤,但其他情况可能就不一样了,具体情况具体分析。
下面再浅浅分析一个变种。
【Leetcode 278】 第一个错误版本
题目 你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
/** * Forward declaration of isBadVersion API.* @param version your guess about first bad version* @return true if current version is bad * false if current version is good* func isBadVersion(version int) bool;*/func firstBadVersion(n int) int {l, r, m, tar := 1, n, 0, 0for l <= r {m = (r-l)/2 + lif isBadVersion(m) {r = m - 1if tar > m || tar == 0 {tar = m} else {break}} else {l = m + 1}} return tar
}
本题变在并不是匹配上接口,要做的是找到判定为 false 的最小值。
你就需要用一个值来暂存这个返回值。然后不断二分,直到找不到比他更小的值为止。
所以,你的退出条件不是匹配到 true 就退出,而是找不到比他更小的 true 再退出。等于或者大于都退出。
end
相关文章:

【LeetCode 704】【Go】二分查找
二分查找题解 一、碎碎念 从本周开始,重新更新刷题记录了哈。 基于费曼学习法的原理,最好的输入是输出,所以与大家分享。 鉴于目前这个糟糕的市场环境,还是要练好自己的基本技术,万一那天就被迫 N 1了,你…...

【代码随想录训练营】【Day23】第六章|二叉树|669. 修剪二叉搜索树 |108.将有序数组转换为二叉搜索树|538.把二叉搜索树转换为累加树
修剪二叉搜索树 题目详细:LeetCode.669 做这道题之前建议先看视频讲解,没有想象中那么复杂:代码随想录—修剪二叉搜索树 由题可知,需要删除节点值不在区间内的节点,所以可以得到三种情况: 情况一&#…...
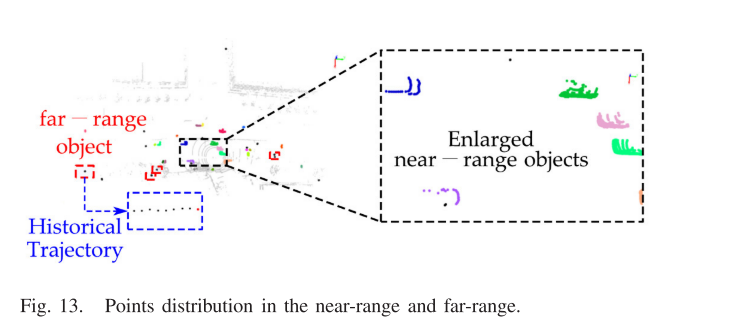
CV——day78 读论文:通过静态背景构建扩展低通道路边雷达的探测距离(目标是规避风险)
Extending the Detection Range for Low-Channel Roadside LiDAR by Static Background Construction 通过静态背景构建扩展低通道路边雷达的探测距离I. INTRODUCTIONII. RELATED WORKA. LiDAR-Based 3-D Vehicle and Road User DetectionB. LiDAR Data Background FilteringC.…...
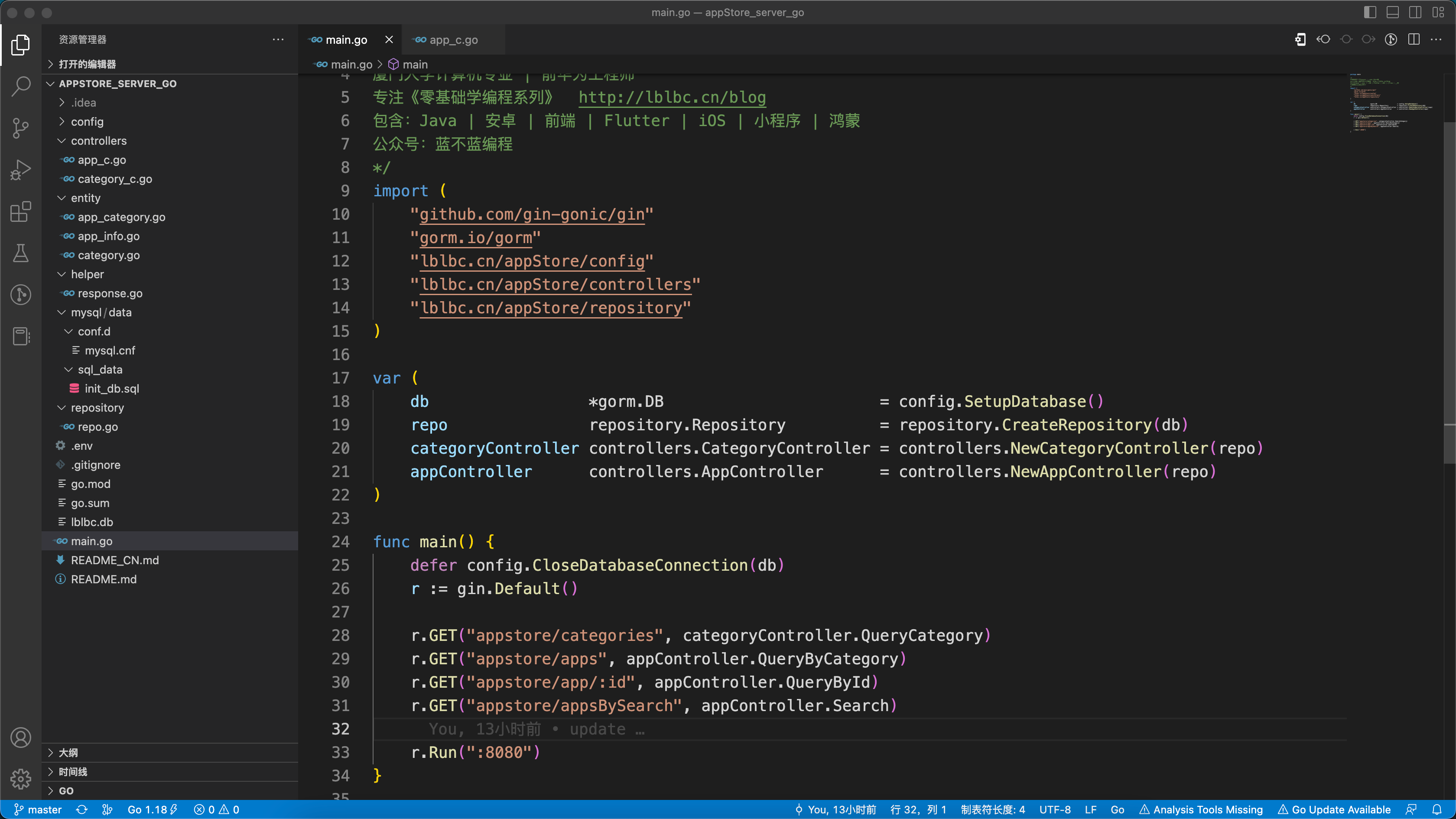
【编程入门】应用市场(go语言版)
背景 前面已输出多个系列: 《十余种编程语言做个计算器》 《十余种编程语言写2048小游戏》 《17种编程语言10种排序算法》 《十余种编程语言写博客系统》 《十余种编程语言写云笔记》 《N种编程语言做个记事本》 目标 为编程初学者打造入门学习项目,使…...
没有界面连接互联网方法)
Linux(openEuler)没有界面连接互联网方法
前言: 系统版本openEuleropenEuler-22.03-LTS-x86_64-dvd 我们在安装linux之后,一般都是无界面的情况。大部分情况都是需要自己安装界面的,如果路由器的情况下直接插上网络就好了。下面就开始介绍两种方法进行linxu网络的连接。 注意: 小编是使用的第一…...

第一天 软考中级--嵌入式系统设计师考试复习教程开始了
第一天 嵌入式系统设计师考试复习教程 第二天 软考中级--嵌入式系统设计师考试考试大纲解析 目录...

分享 10 个高频 Python 面试题
Python 很容易学会,但很难掌握。你可以在几天内了解它的基本语法,但是要能够用 Python 开发出足够好的商业软件,多年的实践是必须的。因为,无论你使用哪种编程语言,你都必须对其复杂的内部机制有足够的了解,…...
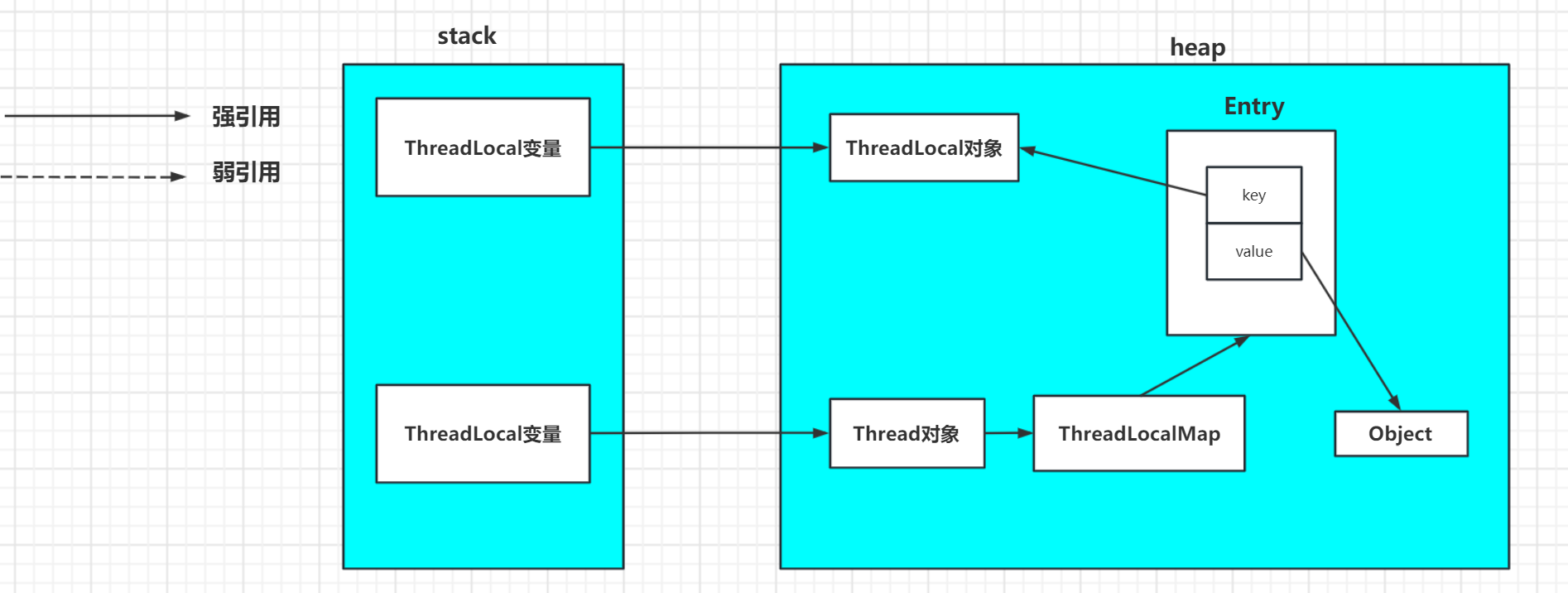
ThreadLocal原理、结构、源码解析
文章目录一、Thread简介1.什么是ThreadLocal2.为什么要是用ThreadLocal2.1Synchronized、Lock保证线程安全2.2ThreadLocal保证线程安全3.ThreadLocal和Synchronized的区别二、ThreadLocal原理1.Thread抽象内部结构2.ThreadLocal源码2.1Thread、ThreadLocal、ThreadLocalMap、En…...

分布式之PBFT算法
写在前面 在分布式之拜占庭问题 一文中我们分析了拜占庭问题,并一起看了支持拜占庭容错的口信消息性和签名消息性算法,但是这两种算法都有一个非常严重的问题,就是消息数量太多,通信的成本太大,消息数量复杂度为O(n ^…...
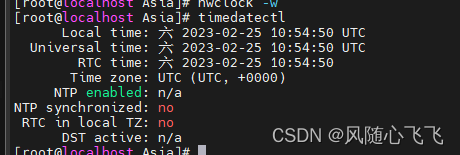
Linux 操作系统——查看/修改系统时区、时间、本地时间修改为UTC
文章目录1.背景描述2.知识储备3.解决步骤1. 查看当前时区2.修改设置Linux服务器时区3.复制相应的时区文件,替换系统时区文件;或者创建链接文件4. 查看和修改Linux的时间5. 硬件时间和系统时间的 相互同步1.背景描述 最近一个项目日期采用java8的LocalDa…...

CSS数据类型以及符号
css数据类型定义的是css属性中具有代表性的值,在规范的语法格式中,使用关键字外加一对 <和>表示,例如数值类型<number>、色值类型<color>等。 举个例子:background-image这个css属性语法结构如下: …...
LeetCode-54. 螺旋矩阵
题目来源 54. 螺旋矩阵 题目思路 while循环只遍历"环",不成环就不遍历了 四个边界 上边界 top : 0下边界 bottom : matrix.length - 1左边界 left : 0右边界 right : matrix[0].length - 1 矩阵不一定是方阵 top < bottom && left < r…...

【Python入门第十八天】Python For 循环
Python For 循环 for 循环用于迭代序列(即列表,元组,字典,集合或字符串)。 这与其他编程语言中的 for 关键字不太相似,而是更像其他面向对象编程语言中的迭代器方法。 通过使用 for 循环,我们…...

Qt图片定时滚动播放器
目录参考结构PicturePlay.promain.cpppictureplay.hpictureplay.cpppictureplay.ui效果源码参考 Qt图片浏览器 QT制作一个图片播放器 Qt中自适应的labelpixmap充满窗口后,无法缩小只能放大 可以显示jpg、jpeg、png、bmp。可以从电脑上拖动图到窗口并显示出来或者打开…...

李宏毅2023春季机器学习课程
目录2021&2022课程重磅须知我维护的其他项目更新日志课程地址课程资料直链课程作业直链其他优质课程2021&2022课程 CSDN Github 重磅须知 为方便所有网课资料与优质电子书籍的实时更新维护,创建一个在线实时网盘文件夹; 网盘获取方式&#…...

计算机操作系统知识点汇总
计算机操作系统选择填空题,300知识点,包含操作系统概论、处理机管理、内存管理、设备管理、文件管理等,为大学生期末创造奇迹提供无限可能 1、填空题 1、操作系统是对计算机资源进行管理的软件 2、操作系统是提供了处理机管理、 存储器管理…...

【离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表】
离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表离线数仓-8-数据仓库开发DWD层设计要点-交易域相关事实表一、DWD层设计要点二、交易域相关事实表1.交易域加购事务事实表1.加购事务事实表 前期梳理2.加购事务事实表 DDL表设计分析3.加购事务事实表 加载数据分析1.首日全…...
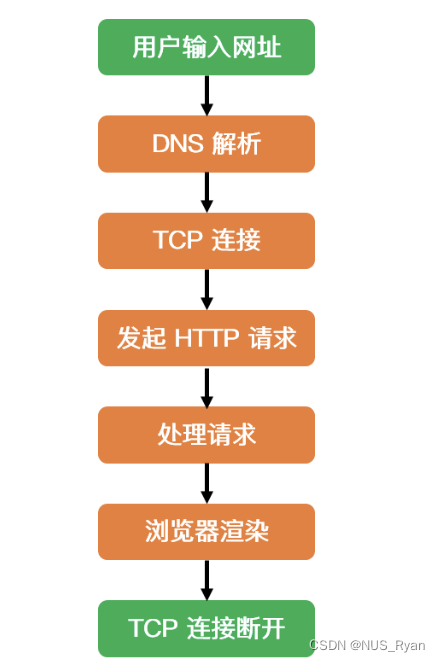
计算机网络(七):DNS协议和原理,DNS为什么用UDP,网页解析的全过程
文章目录一、什么是DNS二、DNS的作用三、DNS作用四、DNS为什么用UDP五、如果打开一个网站很慢,要如何排查六、网页解析的全过程一、什么是DNS DNS是域名系统的英文缩写,是一种组织成域层次结构的计算机和网络服务命名系统,用于TCP/IP网络。 …...
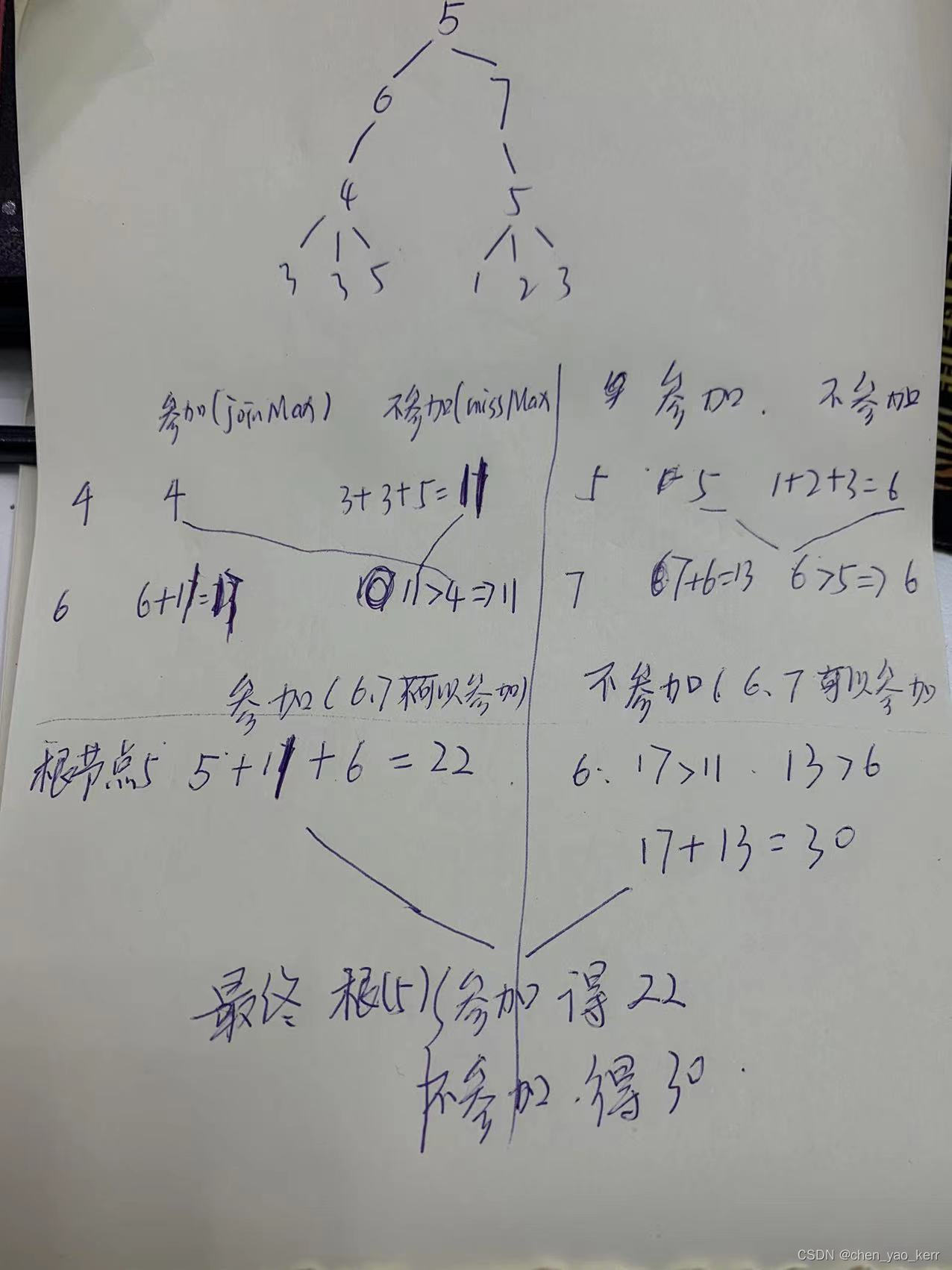
算法23:多叉树_派对的最大快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每…...

中国ETC行业市场规模及未来发展趋势
中国ETC行业市场规模及未来发展趋势编辑根据市场调研在线网发布的2023-2029年中国ETC行业发展策略分析及战略咨询研究报告分析:随着政府坚持实施绿色出行政策,ETC行业也受到了极大的支持。根据中国智能交通协会统计,2017年中国ETC行业市场规模…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
