深入浅出排序算法之归并排序
目录
1. 归并排序的原理
1.1 二路归并排序执行流程
2. 代码分析
2.1 代码设计
3. 性能分析
4. 非递归版本
1. 归并排序的原理
“归并”一词的中文含义就是合并、并入的意思,而在数据结构中的定义是将两个或者两个以上的有序表组合成一个新的有序表。
归并排序(Merging Sort)就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列的长度为1,然后两两归并,得到[n/2](表示不小于x的最小整数)个长度为2或1的有序子序列;再两两归并,……,如此重复,直至得到一个长度为n的有序序列为止,这种排序方法成为2路归并排序。
1.1 二路归并排序执行流程
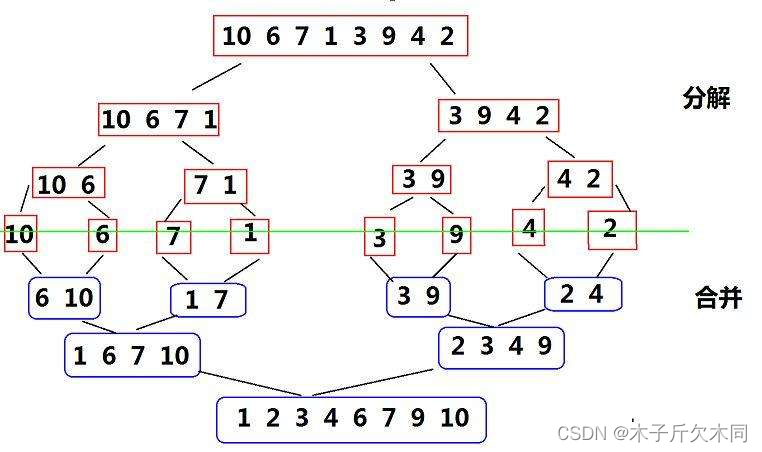
原始序列:49 38 65 97 76 13 27
(1)将原始序列看成7个只含有一个关键字的子序列,显然这些子序列都是有序的。
子序列1:49;子序列2:38;子序列3:65;子序列4:97;子序列5:76;子序列6:13;子序列7:27
(2)两两归并,形成若干有序二元组,即49和38归并成{38 49},65和97归并成{65 97},76和13归并成{13 76},27没有归并对象,保持原样{27}。第一趟二路归并排序结束,结果如下:
{38 49},{65 97},{13 76},{27}
(3)再将这个序列看成若干二元组子序列
子序列1:38 49;子序列2:65 97;子序列3:13 76;子序列4:27;
最后一个子序列长度可能是1,也可能是2。
(4)继续两两归并,形成若干有序四元组(同样,最后的子序列中不一定有4个关键字),即{38 49}和{65 97}归并形成{38 49 65 97},{13 76}和{27}归并形成{13 27 76}。第二趟二路归并排序结束,结果如下:
{38 49 65 97},{13 27 76}
(5)最后只有两个子序列了,再进行一次归并,就可完成整个二路归并排序,结果如下:
13 27 38 49 65 76 97
2. 代码分析
大家先看看有没有思路!
3,2,1 开始我的表演哈哈哈!
请看图解:

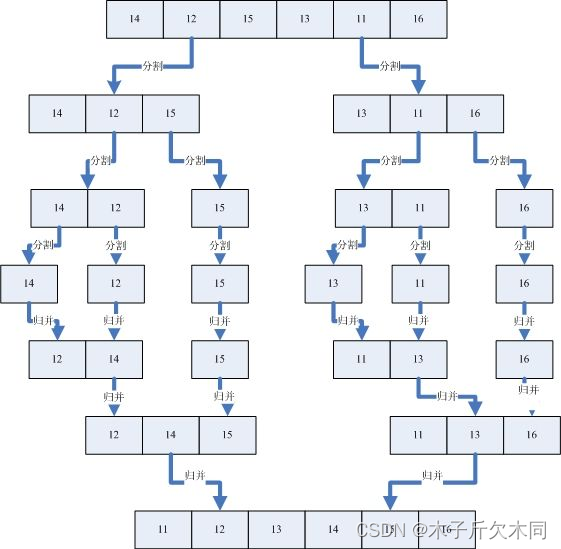
2.1 代码设计
根据图解我们要怎么设计方法呢?
我打算把分解功能写成一个方法,合并功能写成一个方法。具体实现如下:
public static void mergeSort1(int[] array){mergeSortDivide(array,0, array.length - 1);}//分解private static void mergeSortDivide(int[] array,int left,int right){//终止条件:left > rightwhile(left >= right){return;}int mid = (left+right)/2;//递归左子序列mergeSortDivide(array,left,mid);//递归右子序列mergeSortDivide(array,mid+1,right);//合并merge(array,left,right,mid);}//合并private static void merge(int[] array,int start,int end,int mid){//左子序列从start开始int s1 = start;//右子序列从mid+1开始int s2 = mid + 1;//新建一个数组,作为复制数组int[] tmp = new int[end - start + 1];//k表示中间数组的元素下标int k = 0;//开始比较while(s1 <= mid && s2 <= end){if(array[s1] <= array[s2]){//将小的值赋值给tmp[k]//小伙伴们这可以思考一下:为什么不能先写array[s2] <= array[s1]?//等下看我下面的解析!tmp[k++] = array[s1++];} else{//array[s2] <= array[s1]的情况tmp[k++] = array[s2++];}}//有剩余的数组//左子序列while(s1 <= mid){tmp[k++] = array[s1++];}//右子序列while(s2 <= end){tmp[k++] = array[s2++];}//将tmp数组的值赋值给array数组for(int i = 0;i<tmp.length;i++){array[i+start] = tmp[i];}}回答问题:为什么不能先写array[s2] <= array[s1]?
答:归并排序是稳定的。如果先写array[s2] <= array[s1],那么在s2开始的元素与s1开始的元素相等的话,例如:1<=1,那么本该在后面的1就会移到前面,导致这段代码实现的归并排序不稳定了!
3. 性能分析
| 时间复杂度 | 空间复杂度 |
| O(n*log(n)) | O(n) |

4. 非递归版本
上面的版本是递归版本,接下来是非递归版本。

private static void merge(int[] array,int start,int end,int mid) {int s1 = start;//int e1 = mid;int s2 = mid+1;//int e2 = end;int[] tmp = new int[end-start+1];int k = 0;//tmp数组的下标while (s1 <= mid && s2 <= end) {if(array[s1] <= array[s2]) {tmp[k++] = array[s1++];}else {tmp[k++] = array[s2++];}}while (s1 <= mid) {tmp[k++] = array[s1++];}while (s2 <= end) {tmp[k++] = array[s2++];}for (int i = 0; i < tmp.length; i++) {array[i+start] = tmp[i];}}public static void mergeSort(int[] array) {int gap = 1;while (gap < array.length) {// i += gap * 2 当前gap组的时候,去排序下一组for (int i = 0; i < array.length; i += gap * 2) {int left = i;int mid = left+gap-1;//有可能会越界if(mid >= array.length) {mid = array.length-1;}int right = mid+gap;//有可能会越界if(right>= array.length) {right = array.length-1;}merge(array,left,right,mid);}//当前为2组有序 下次变成4组有序gap *= 2;}}相关文章:

深入浅出排序算法之归并排序
目录 1. 归并排序的原理 1.1 二路归并排序执行流程 2. 代码分析 2.1 代码设计 3. 性能分析 4. 非递归版本 1. 归并排序的原理 “归并”一词的中文含义就是合并、并入的意思,而在数据结构中的定义是将两个或者两个以上的有序表组合成一个新的有序表。 归并排序…...

opencv dnn模块 示例(19) 目标检测 object_detection 之 yolox
文章目录 0、前言1、网络介绍1.1、输入1.2、Backbone主干网络1.3、Neck1.4、Prediction预测输出1.4.1、Decoupled Head解耦头1.4.2、Anchor-Free1.4.3、标签分配1.4.4、Loss计算 1.5、Yolox-s、l、m、x系列1.6、轻量级网络研究1.6.1、轻量级网络1.6.2、数据增强的优缺点 1.7、Y…...

微信小程序阻止返回事件
需求场景 当在一个表单页面 填写了很多数据,或者编辑页面数据发生变动之后,这时候返回上一个页面需要提醒用户是否返回的弹框 实现方法一(ios会存在一定的问题) 在onLoad生命周期里 注册 wx.enableAlertBeforeUnload({message: "您内容已更新,还没保存,确定要退出吗?&…...

YOLOv7改进:新颖的上下文解耦头TSCODE,即插即用,各个数据集下实现暴力涨点
💡💡💡本文属于原创独家改进:上下文解耦头TSCODE,进行深、浅层的特征融合,最后再分别输入到头部进行相应的解码输出,实现暴力暴力涨点 上下文解耦头TSCODE| 亲测在多个数据集实现暴力涨点,对遮挡场景、小目标场景提升也明显; 收录: YOLOv7高阶自研专栏介绍: …...
Unity中Shader阴影的接收
文章目录 前言一、阴影接受的步骤1、在v2f中添加UNITY_SHADOW_COORDS(idx),unity会自动声明一个叫_ShadowCoord的float4变量,用作阴影的采样坐标.2、在顶点着色器中添加TRANSFER_SHADOW(o),用于将上面定义的_ShadowCoord纹理采样坐标变换到相应的屏幕空间…...

✔ ★【备战实习(面经+项目+算法)】 10.22学习时间表(总计学习时间:4.5h)(算法刷题:7道)
✔ ★【备战实习(面经项目算法)】 坚持完成每天必做如何找到好工作1. 科学的学习方法(专注!效率!记忆!心流!)2. 每天认真完成必做项,踏实学习技术 认真完成每天必做&…...
Amazonlinux2023(AL2023)获取metadata
今年AWS发布了新的Amazonlinux2023版本,其中获取metadata元数据方式发生了一点改变。 早些时候,在 Amazon Linux 2 中,使用以下命令获取实例元数据 http://169.254.169.254/latest/meta-data/ 具体可以获取的元数据类别可以查阅如下aws官方…...
C++(Chapter 3)
C(三) 1.引用 1.引用的概念 引用的概念:引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空间,它和它引用的变量共用同一块内存空间。 引用的语法:类型& 引用变量名(对象名) 引用实体 ; 例如: #i…...

优化单元测试效率:Spring 工程启动耗时统计
相关文章: Java Agent 的简单使用 本文相关代码地址:https://gitee.com/dongguabai/blog 单元测试在软件项目的可持续发展中扮演着不可或缺的角色,这一点毫无疑问。不久前,公司大佬在内部分享时也提到过:单元测试是…...

华纳云:连接mysql出现2059错误怎么解决
MySQL连接错误2059通常表示MySQL服务器拒绝了连接。这种错误可能由多种原因引起,以下是一些可能的解决方法: 检查MySQL服务器是否正在运行: 确保MySQL服务器正在正常运行。您可以使用以下命令检查MySQL服务器的状态: systemctl st…...

零基础Linux_22(多线程)线程控制和和C++的多线程和笔试选择题
目录 1. 线程控制 1.1 线程创建(pthread_create) 1.2 线程结束(pthread_exit) 1.3 线程等待(pthread_join) 1.4 线程取消(pthread_cancel结束) 1.5 线程tid(pthread_self()) 1.6 线程局部存储(__thread) 1.7 线程分离(pthread_detach) 2. C的多线程 3. 笔试选择题 答…...
docker版本的Jenkins安装与更新技巧
因为jenkins/jenkins镜像默认带的jenkins版本比较低,导致安装完以后,很多插件因为版本问题无法安装。以下是最权威,最方便的安装教程。 1. 创建本地挂载目录 mkdir -p /mnt/dockerdata/jenkins/home/2. 修改挂载目录权限 chown -R 1000:10…...
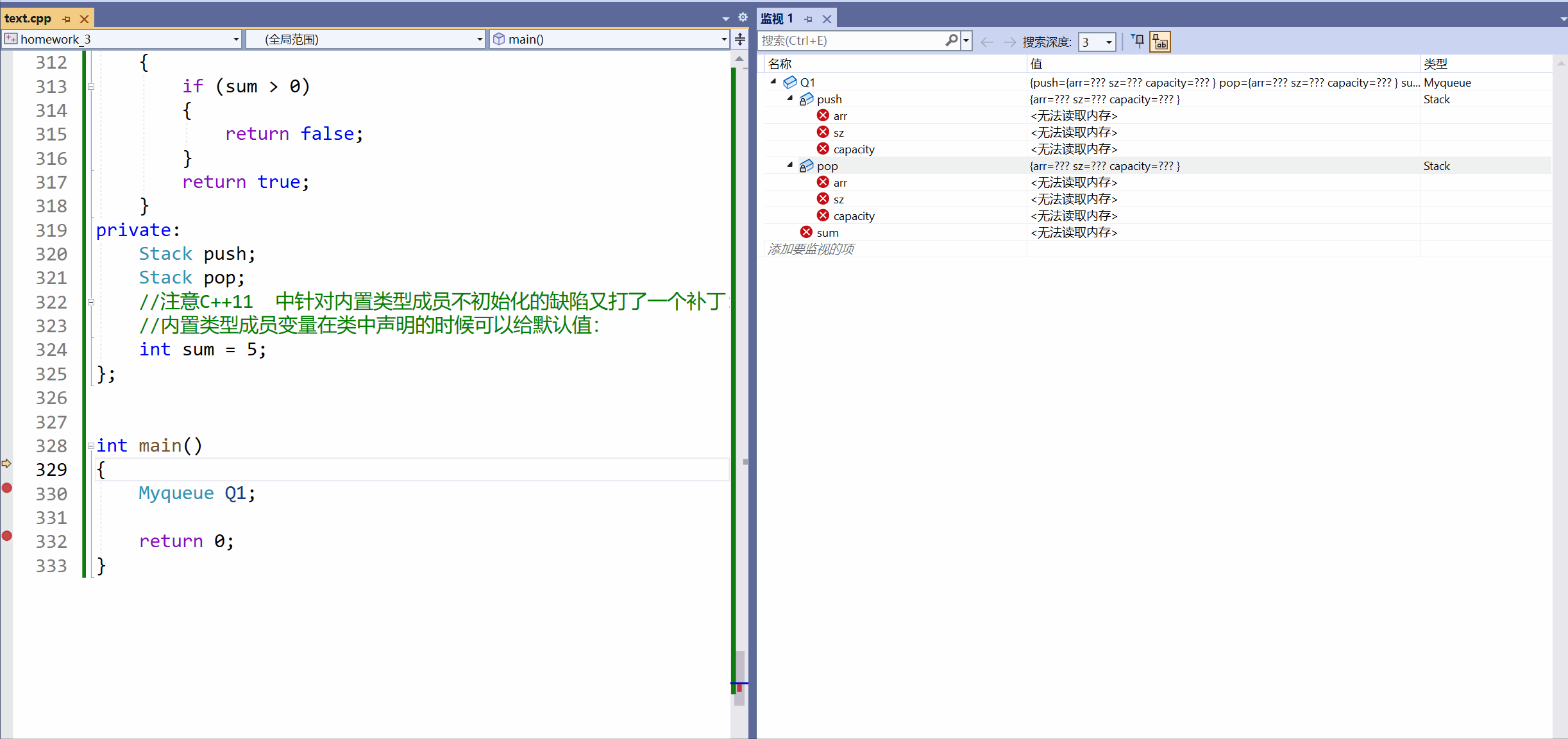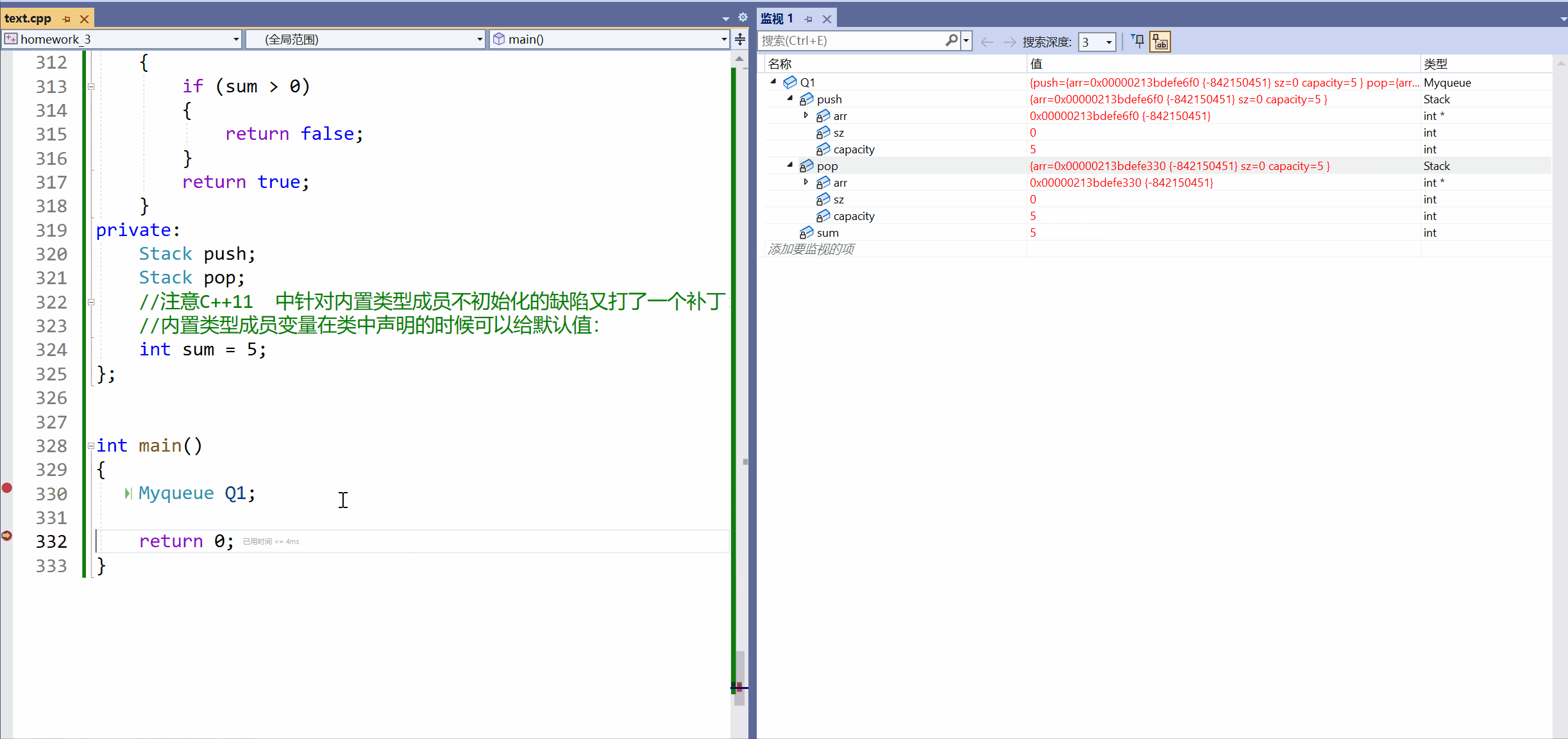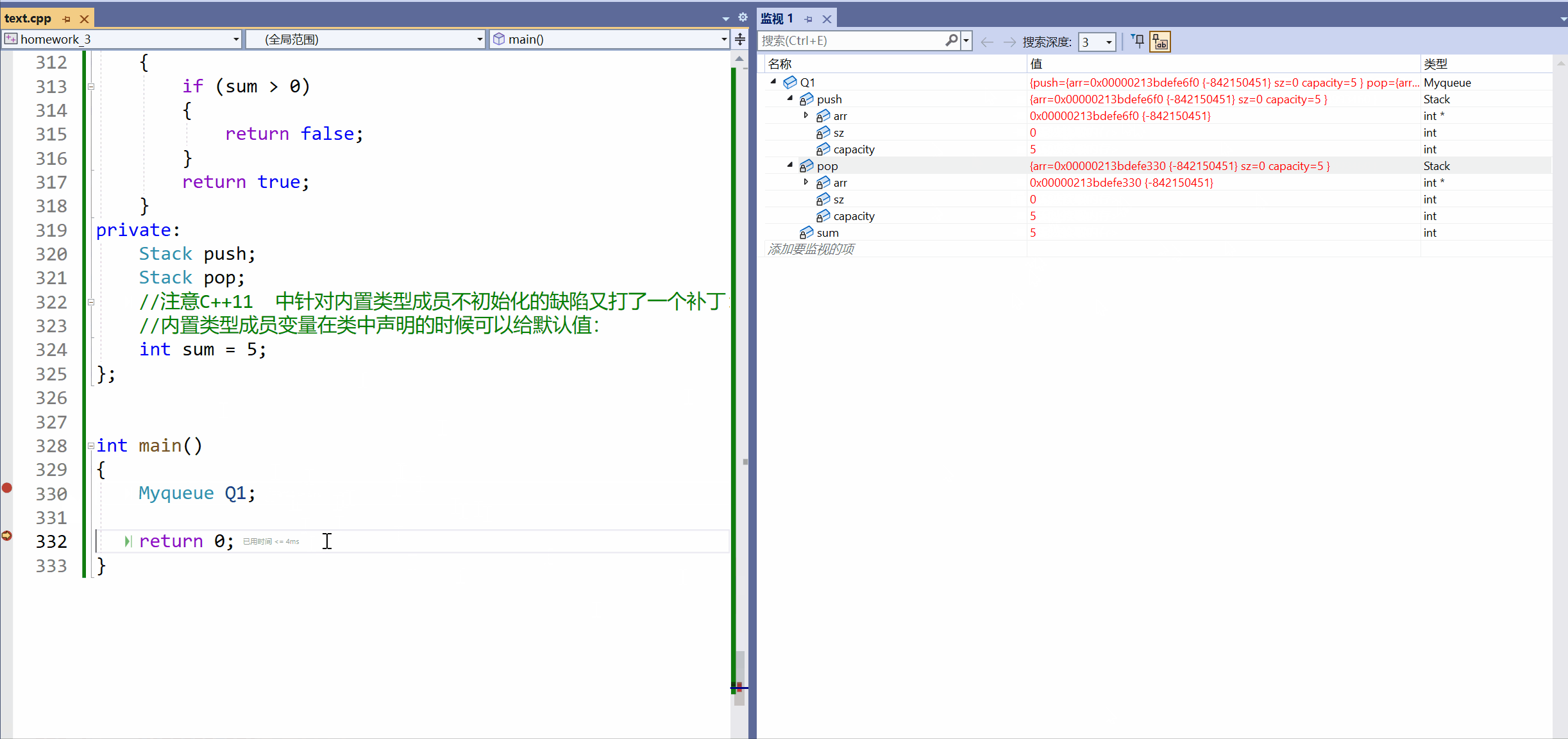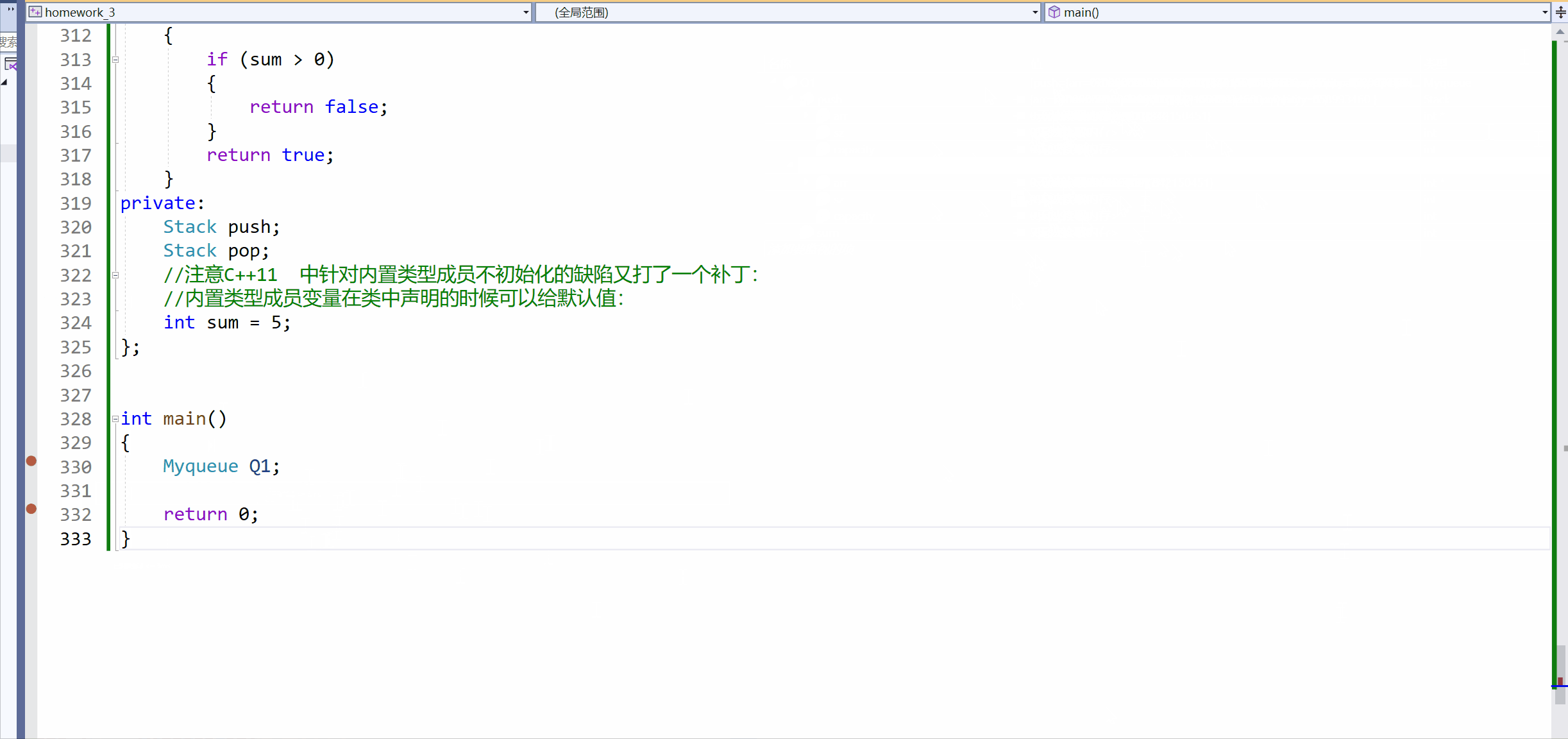
[C++]3.类和对象下(this指针补充)+ 类和对象中构造函数和析构函数。
类和对象下(this指针补充) 类和对象中构造函数和析构函数 一.this补充:1.概念总结:2.两个问题: 二.构造函数和析构函数:一.类的默认构造:1.初始化和清理:2.拷贝复制:3.取…...

OpenLDAP LDIF详解
手把手一步步搭建LDAP服务器并加域 有必要理解的概念LDAPWindows Active Directory 服务器配置安装 OpenLDAP自定义安装修改对象(用户和分组等)修改olcSuffix 和 olcRootDN 属性增加olcRootPW 属性修改olcAccess属性验证新属性值 添加对象(用…...

Leetcode.33 搜索旋转排序数组
题目链接 Leetcode.33 搜索旋转排序数组 mid 题目描述 整数数组 n u m s nums nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前, n u m s nums nums 在预先未知的某个下标 k ( 0 ≤ k < n u m s . l e n g t h )…...

ES 8.x 向量检索性能测试 把向量检索性能提升100倍!
向量检索不仅在的跨模态检索场景中应用广泛,随着chat gpt的或者,利用es的向量检索,在Ai领域发挥着越来越大的作用。 本文,主要测试es的向量检索性能。我从8.x就开始关注ES的向量检索了。当前ES已经发布到 8.10 版本。以下是官方文…...
云计算——ACA学习 云计算架构
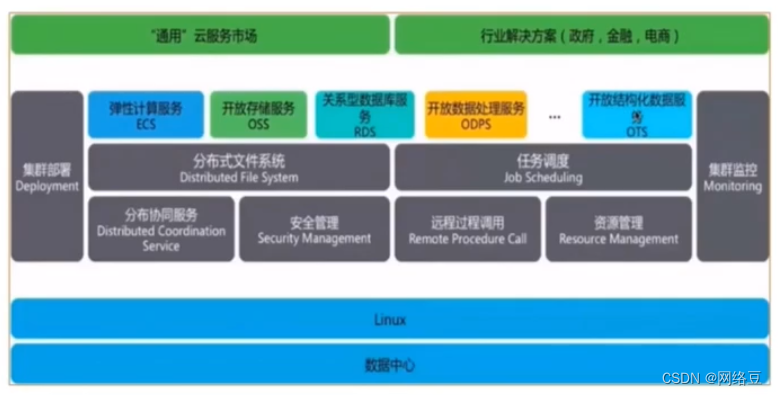
作者简介:一名云计算网络运维人员、每天分享网络与运维的技术与干货。 公众号:网络豆云计算学堂 座右铭:低头赶路,敬事如仪 个人主页: 网络豆的主页 目录 写在前面 前期回顾 本期介绍 一.云计算架…...
基于深度学习实现一张单图,一个视频,一键换脸,Colab脚本使用方法,在线版本,普通人也可以上传一张图片体验机器学习一键换脸
基于深度学习实现一张单图,一个视频,一键换脸,Colab脚本使用方法,在线版本,普通人也可以上传一张图片体验机器学习一键换脸。 AI领域人才辈出,突然就跳出一个大佬“s0md3v”,开源了一个单图就可以进行视频换脸的项目。 项目主页给了一张换脸动图非常有说服力,真是一图…...

leetcode 21
递归的方式 class Solution { public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {if(l1 nullptr){return l2;}else if(l2 nullptr){return l1;}else if(l1->val < l2->val){l1->next mergeTwoLists(l1->next, l2);return l1;}else if(l1->va…...
)
【Spring Cloud】openfeign负载均衡方案(和lb发展历史)
文章目录 版本1:原始loadBalancerClient方案版本2:ribbon-loadbalancer方案版本3:openfeign方案(即**方案2openfeign版本**) 本文描述了Spring Cloud微服务中,各个服务间调用的负载均衡方案的升级历史&…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
