A_搜索(A Star)算法
A*搜索(A Star)
不同于盲目搜索,A算法是一种启发式算法(Heuristic Algorithm)。
上文提到,盲目搜索对于所有要搜索的状态结点都是一视同仁的,因此在每次搜索一个状态时,盲目搜索并不会考虑这个状态到底是有利于趋向目标的,还是偏离目标的。
而启发式搜索的启发二字,看起来是不是感觉这个算法就变得聪明一点了呢?正是这样,启发式搜索对于待搜索的状态会进行不同的优劣判断,这个判断的结果将会对算法搜索顺序起到一种启发作用,越优秀的状态将会得到越高的搜索优先级。
我们把对于状态优劣判断的方法称为启发函数*,通过给它评定一个搜索代价来量化启发值。
启发函数应针对不同的使用场景来设计,那么在拼图的游戏中,如何评定某个状态的优劣性呢?粗略的评估方法有两种:
- 可以想到,某个状态它的方块位置放对的越多,说明它能复原目标的希望就越大,这个状态就越优秀,优先选择它就能减少无效的搜索,经过它而推演到目标的代价就会小。所以可求出某个状态所有方块的错位数量来作为评估值,错位越少,状态越优秀。
- 假如让拼图上的每个方块都可以穿过邻近方块,无阻碍地移动到目标位置,那么每个不在正确位置上的方块它距离正确位置都会存在一个移动距离,这个非直线的距离即为曼哈顿距离(Manhattan Distance),我们把每个方块距离其正确位置的曼哈顿距离相加起来,所求的和可以作为搜索代价的值,值越小则可认为状态越优秀。
其实上述两种评定方法都只是对当前状态距离目标状态的代价评估,我们还忽略了一点,就是这个状态距离搜索开始的状态是否已经非常远了,亦即状态结点的深度值。
在拼图游戏中,我们进行的是路径搜索,假如搜索出来的一条移动路径其需要的步数非常多,即使最终能够把拼图复原,那也不是我们希望的路径。所以,路径搜索存在一个最优解的问题,搜索出来的路径所需要移动的步数越少,就越优。
A*算法对某个状态结点的评估,应综合考虑这个结点距离开始结点的代价与距离目标结点的代价。总估价公式可以表示为:
f(n) = g(n) + h(n)
n 表示某个结点,f(n) 表示对某个结点进行评价,值等于这个结点距离开始结点的已知价 g(n) 加上距离目标结点的估算价 h(n)。
为什么说 g(n) 的值是确定已知的呢?在每次生成子状态结点时,子状态的 g 值应在它父状态的基础上 +1,以此表示距离开始状态增加了一步,即深度加深了。所以每一个状态的 g 值并不需要估算,是实实在在确定的值。
影响算法效率的关键点在于 h(n) 的计算,采用不同的方法来计算 h 值将会让算法产生巨大的差异。
- 当增大
h值的权重,即让h值远超g值时,算法偏向于快速寻找到目标状态,而忽略路径长度,这样搜索出来的结果就很难保证是最优解了,意味着可能会多绕一些弯路,通往目标状态的步数会比较多。 - 当减小
h值的权重,降低启发信息量,算法将偏向于注重已搜深度,当h(n)恒为0时,A*算法其实已退化为广度优先搜索了。(这是为照应上文的方便说法。严谨的说法应是退化为 Dijkstra 算法,在本游戏中,广搜可等同为 Dijkstra 算法,关于 Dijkstra 这里不作深入展开。)
以下是拼图状态结点 PuzzleStatus 的估价方法,在实际测试中,使用方块错位数量来作估价的效果不太明显,所以这里只使用曼哈顿距离来作为 **h(n)** 估价,已能达到不错的算法效率。
/// 估算从当前状态到目标状态的代价
- (NSInteger)estimateToTargetStatus:(id<JXPathSearcherStatus>)targetStatus {PuzzleStatus *target = (PuzzleStatus *)targetStatus;// 计算每一个方块距离它正确位置的距离// 曼哈顿距离NSInteger manhattanDistance = 0;for (NSInteger index = 0; index < self.pieceArray.count; ++ index) {// 略过空格if (index == self.emptyIndex) {continue;}PuzzlePiece *currentPiece = self.pieceArray[index];PuzzlePiece *targetPiece = target.pieceArray[index];manhattanDistance +=ABS([self rowOfIndex:currentPiece.ID] - [target rowOfIndex:targetPiece.ID]) +ABS([self colOfIndex:currentPiece.ID] - [target colOfIndex:targetPiece.ID]);}// 增大权重return 5 * manhattanDistance;
}
状态估价由状态类自己负责,A算法只询问状态的估价结果,并进行 f(n) = g(n) + h(b) 操作,确保每一次搜索,都是待搜空间里代价最小的状态,即 f 值最小的状态。
那么问题来了,在给每个状态都计算并赋予上 **f** 值后,如何做到每一次只取 **f** 值最小的那个?
前文已讲到,所有扩展出来的新状态都会放入开放队列中的,如果 A算法也像广搜那样只放在队列尾,然后每次只取队首元素来搜索的话,那么 f 值完全没有起到作用。
事实上,因为每个状态都有 f 值的存在,它们已经有了优劣高下之分,队列在存取它们的时候,应当按其 f 值而有选择地进行入列出列,这时候需要用到优先队列(Priority Queue),它能够每次出列优先级最高的元素。
以下是 A*搜索算法的代码实现:
- (NSMutableArray *)search {if (!self.startStatus || !self.targetStatus || !self.equalComparator) {return nil;}NSMutableArray *path = [NSMutableArray array];[(id<JXAStarSearcherStatus>)[self startStatus] setGValue:0];// 关闭堆,存放已搜索过的状态NSMutableDictionary *close = [NSMutableDictionary dictionary];// 开放队列,存放由已搜索过的状态所扩展出来的未搜索状态// 使用优先队列JXPriorityQueue *open = [JXPriorityQueue queueWithComparator:^NSComparisonResult(id<JXAStarSearcherStatus> obj1, id<JXAStarSearcherStatus> obj2) {if ([obj1 fValue] == [obj2 fValue]) {return NSOrderedSame;}// f值越小,优先级越高return [obj1 fValue] < [obj2 fValue] ? NSOrderedDescending : NSOrderedAscending;}];[open enQueue:self.startStatus];while (open.count > 0) {// 出列id status = [open deQueue];// 排除已经搜索过的状态NSString *statusIdentifier = [status statusIdentifier];if (close[statusIdentifier]) {continue;}close[statusIdentifier] = status;// 如果找到目标状态if (self.equalComparator(self.targetStatus, status)) {path = [self constructPathWithStatus:status isLast:YES];break;}// 否则,扩展出子状态NSMutableArray *childStatus = [status childStatus];// 对各个子状进行代价估算[childStatus enumerateObjectsUsingBlock:^(id<JXAStarSearcherStatus> _Nonnull obj, NSUInteger idx, BOOL * _Nonnull stop) {// 子状态的实际代价比本状态大1[obj setGValue:[status gValue] + 1];// 估算到目标状态的代价[obj setHValue:[obj estimateToTargetStatus:self.targetStatus]];// 总价=已知代价+未知估算代价[obj setFValue:[obj gValue] + [obj hValue]];// 入列[open enQueue:obj];}];}NSLog(@"总共搜索: %@", @(close.count));return path;
}
可以看到,代码基本是以广搜为模块,加入了 f(n) = g(n) + h(b) 的操作,并且使用了优先队列作为开放表,这样改进后,算法的效率是不可同日而语。

相关文章:

A_搜索(A Star)算法
A*搜索(A Star) 不同于盲目搜索,A算法是一种启发式算法(Heuristic Algorithm)。 上文提到,盲目搜索对于所有要搜索的状态结点都是一视同仁的,因此在每次搜索一个状态时,盲目搜索并不会考虑这个状态到底是有利于趋向目标的&#x…...
Tinywebserve学习之linux 用户态内核态
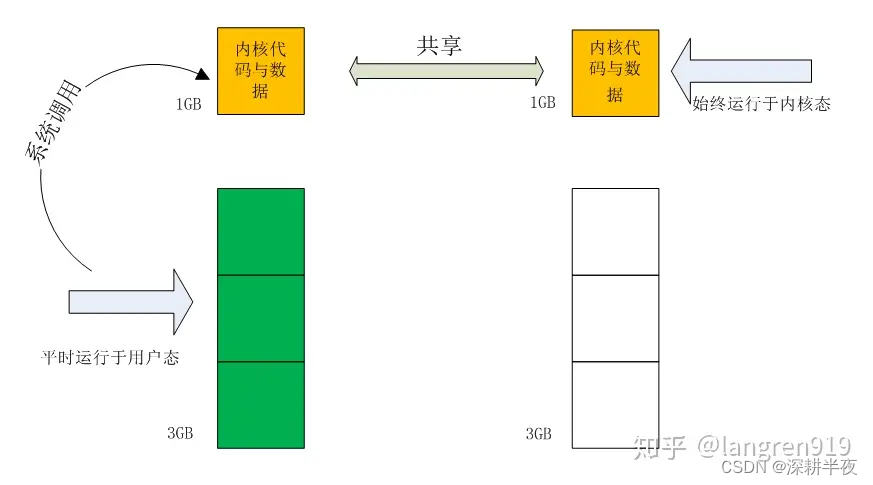
一.CPU指令集权限 指令集是实现CPU实现软件指挥硬件执行的媒介,具体来说每一条汇编语句都对应了一条CPU指令,而非常多的CPU指令再一起组成一个甚至多个集合,指令的集合叫CPU指令集; 因为CPU指令集可以操纵硬件,会造成…...

AI之浅谈
随着ChatGPT的爆火,AI的应用也随之遍地开花,国内国外的各种大模型也都陆续推出,AI的本质是进行数据的分析和整理,其背后的资源来自于互联网时代所积累的大数据基础,这也是深度学习的结果,AI具有不眠不休的特…...

20231024后端研发面经整理
1.如何在单链表O(1)删除节点? 狸猫换太子 2.redis中的key如何找到对应的内存位置? 哈希碰撞的话用链表存 3.线性探测哈希法的插入,查找和删除 插入:一个个挨着后面找,知道有空位 查找:一个个挨着后面找…...

【前段基础入门之】=>CSS3新增渐变颜色属性
导语: CSS3 新增了,渐变色 的解决方案,这使得我们可以绘制出更加生动的炫酷的的配色效果 线性渐变 多个颜色之间的渐变, 默认从上到下渐变 background-image: linear-gradient(red,yellow,green); /*默认从上到下渐变*/默认从上…...

深入浅出排序算法之归并排序
目录 1. 归并排序的原理 1.1 二路归并排序执行流程 2. 代码分析 2.1 代码设计 3. 性能分析 4. 非递归版本 1. 归并排序的原理 “归并”一词的中文含义就是合并、并入的意思,而在数据结构中的定义是将两个或者两个以上的有序表组合成一个新的有序表。 归并排序…...

opencv dnn模块 示例(19) 目标检测 object_detection 之 yolox
文章目录 0、前言1、网络介绍1.1、输入1.2、Backbone主干网络1.3、Neck1.4、Prediction预测输出1.4.1、Decoupled Head解耦头1.4.2、Anchor-Free1.4.3、标签分配1.4.4、Loss计算 1.5、Yolox-s、l、m、x系列1.6、轻量级网络研究1.6.1、轻量级网络1.6.2、数据增强的优缺点 1.7、Y…...

微信小程序阻止返回事件
需求场景 当在一个表单页面 填写了很多数据,或者编辑页面数据发生变动之后,这时候返回上一个页面需要提醒用户是否返回的弹框 实现方法一(ios会存在一定的问题) 在onLoad生命周期里 注册 wx.enableAlertBeforeUnload({message: "您内容已更新,还没保存,确定要退出吗?&…...

YOLOv7改进:新颖的上下文解耦头TSCODE,即插即用,各个数据集下实现暴力涨点
💡💡💡本文属于原创独家改进:上下文解耦头TSCODE,进行深、浅层的特征融合,最后再分别输入到头部进行相应的解码输出,实现暴力暴力涨点 上下文解耦头TSCODE| 亲测在多个数据集实现暴力涨点,对遮挡场景、小目标场景提升也明显; 收录: YOLOv7高阶自研专栏介绍: …...
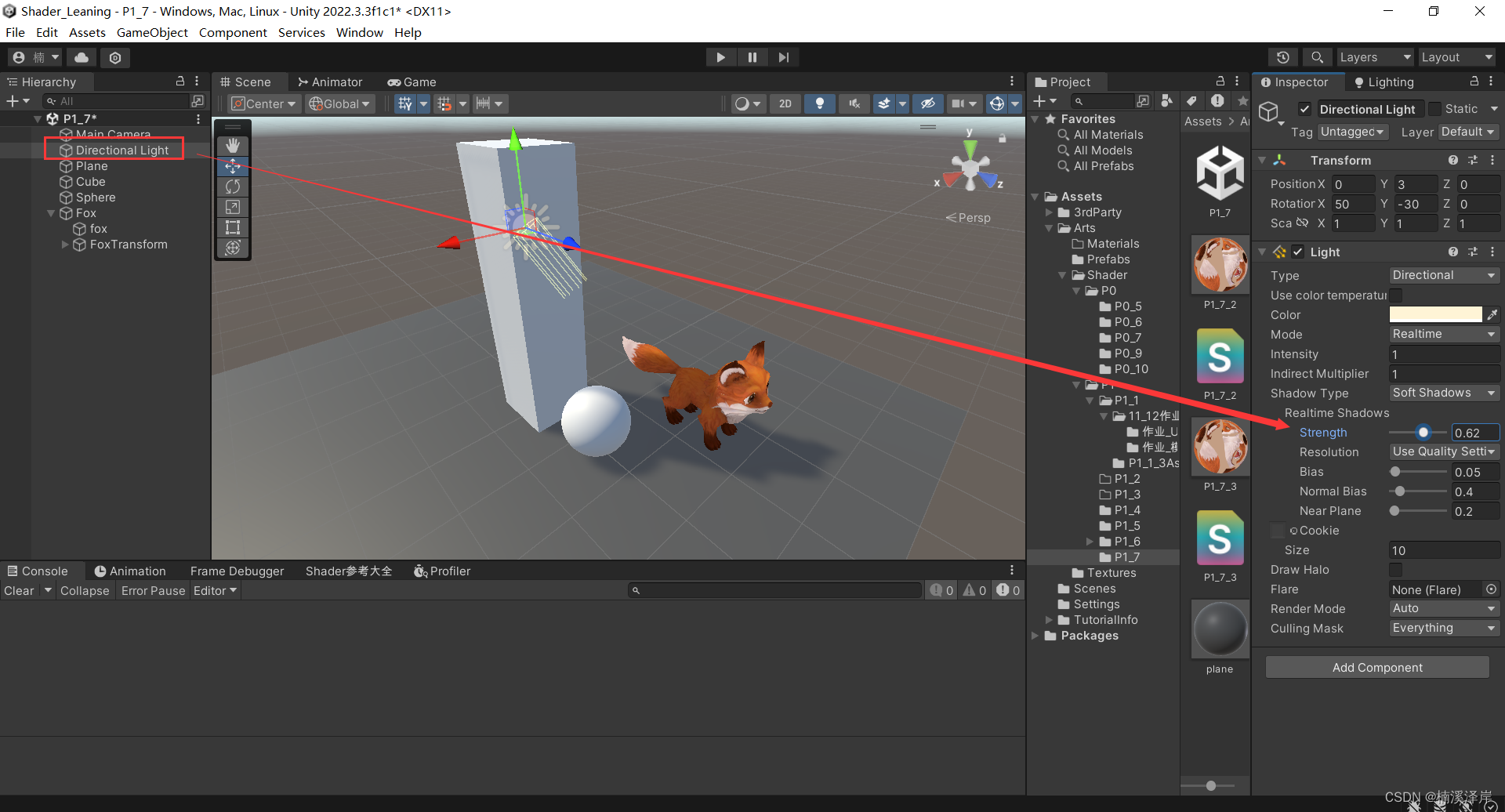
Unity中Shader阴影的接收
文章目录 前言一、阴影接受的步骤1、在v2f中添加UNITY_SHADOW_COORDS(idx),unity会自动声明一个叫_ShadowCoord的float4变量,用作阴影的采样坐标.2、在顶点着色器中添加TRANSFER_SHADOW(o),用于将上面定义的_ShadowCoord纹理采样坐标变换到相应的屏幕空间…...

✔ ★【备战实习(面经+项目+算法)】 10.22学习时间表(总计学习时间:4.5h)(算法刷题:7道)
✔ ★【备战实习(面经项目算法)】 坚持完成每天必做如何找到好工作1. 科学的学习方法(专注!效率!记忆!心流!)2. 每天认真完成必做项,踏实学习技术 认真完成每天必做&…...
Amazonlinux2023(AL2023)获取metadata
今年AWS发布了新的Amazonlinux2023版本,其中获取metadata元数据方式发生了一点改变。 早些时候,在 Amazon Linux 2 中,使用以下命令获取实例元数据 http://169.254.169.254/latest/meta-data/ 具体可以获取的元数据类别可以查阅如下aws官方…...
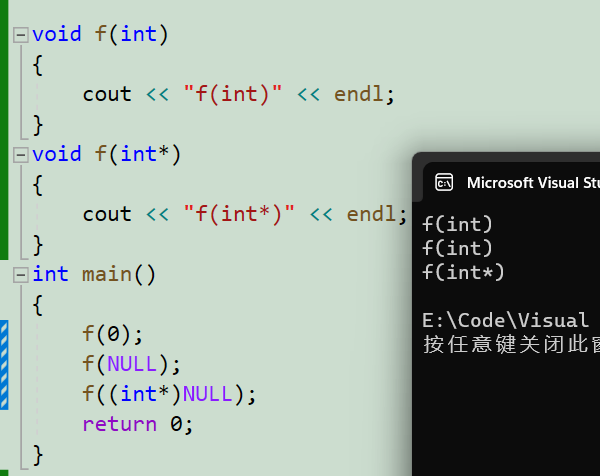
C++(Chapter 3)
C(三) 1.引用 1.引用的概念 引用的概念:引用不是新定义一个变量,而是给已存在变量取了一个别名,编译器不会为引用变量开辟内存空间,它和它引用的变量共用同一块内存空间。 引用的语法:类型& 引用变量名(对象名) 引用实体 ; 例如: #i…...

优化单元测试效率:Spring 工程启动耗时统计
相关文章: Java Agent 的简单使用 本文相关代码地址:https://gitee.com/dongguabai/blog 单元测试在软件项目的可持续发展中扮演着不可或缺的角色,这一点毫无疑问。不久前,公司大佬在内部分享时也提到过:单元测试是…...

华纳云:连接mysql出现2059错误怎么解决
MySQL连接错误2059通常表示MySQL服务器拒绝了连接。这种错误可能由多种原因引起,以下是一些可能的解决方法: 检查MySQL服务器是否正在运行: 确保MySQL服务器正在正常运行。您可以使用以下命令检查MySQL服务器的状态: systemctl st…...

零基础Linux_22(多线程)线程控制和和C++的多线程和笔试选择题
目录 1. 线程控制 1.1 线程创建(pthread_create) 1.2 线程结束(pthread_exit) 1.3 线程等待(pthread_join) 1.4 线程取消(pthread_cancel结束) 1.5 线程tid(pthread_self()) 1.6 线程局部存储(__thread) 1.7 线程分离(pthread_detach) 2. C的多线程 3. 笔试选择题 答…...
docker版本的Jenkins安装与更新技巧
因为jenkins/jenkins镜像默认带的jenkins版本比较低,导致安装完以后,很多插件因为版本问题无法安装。以下是最权威,最方便的安装教程。 1. 创建本地挂载目录 mkdir -p /mnt/dockerdata/jenkins/home/2. 修改挂载目录权限 chown -R 1000:10…...
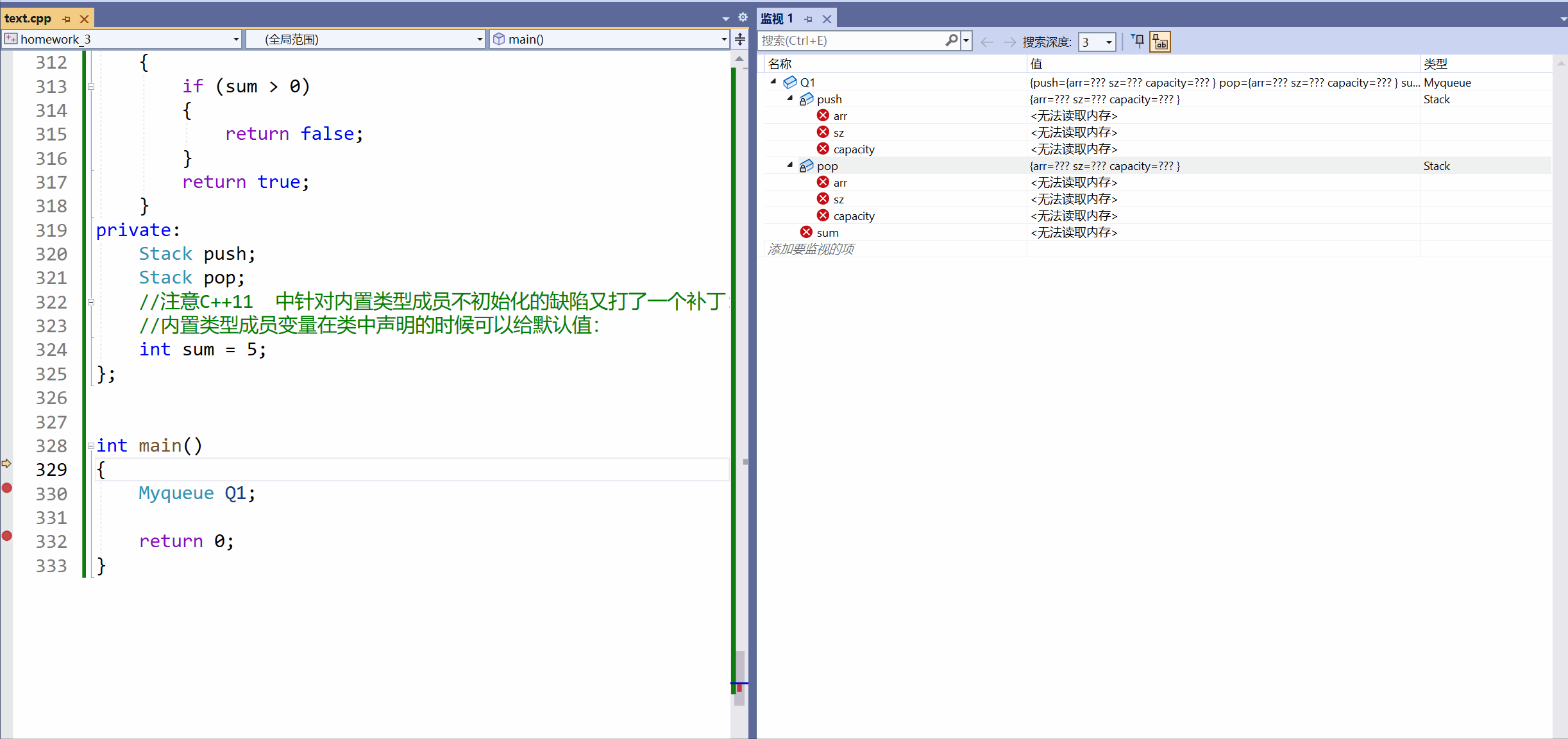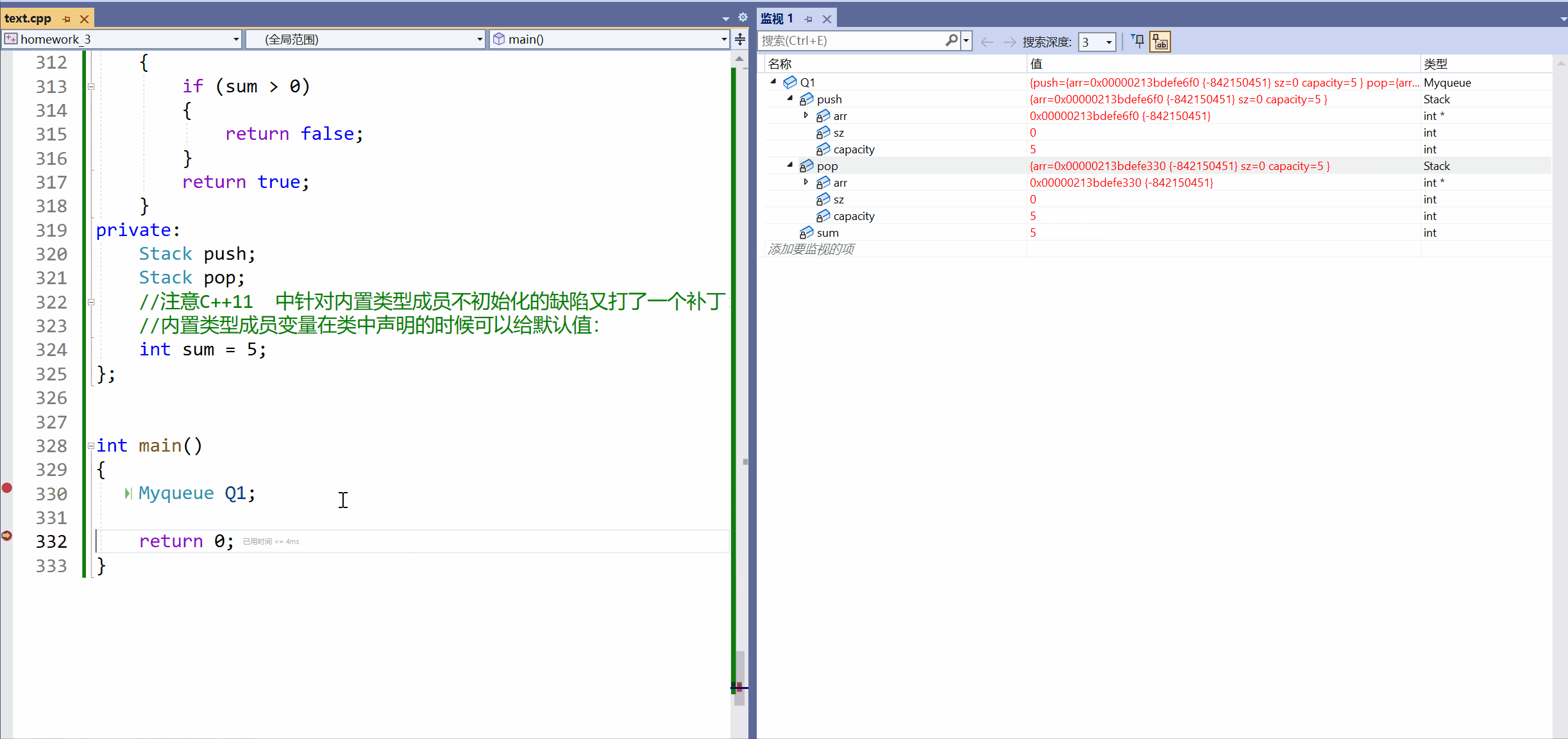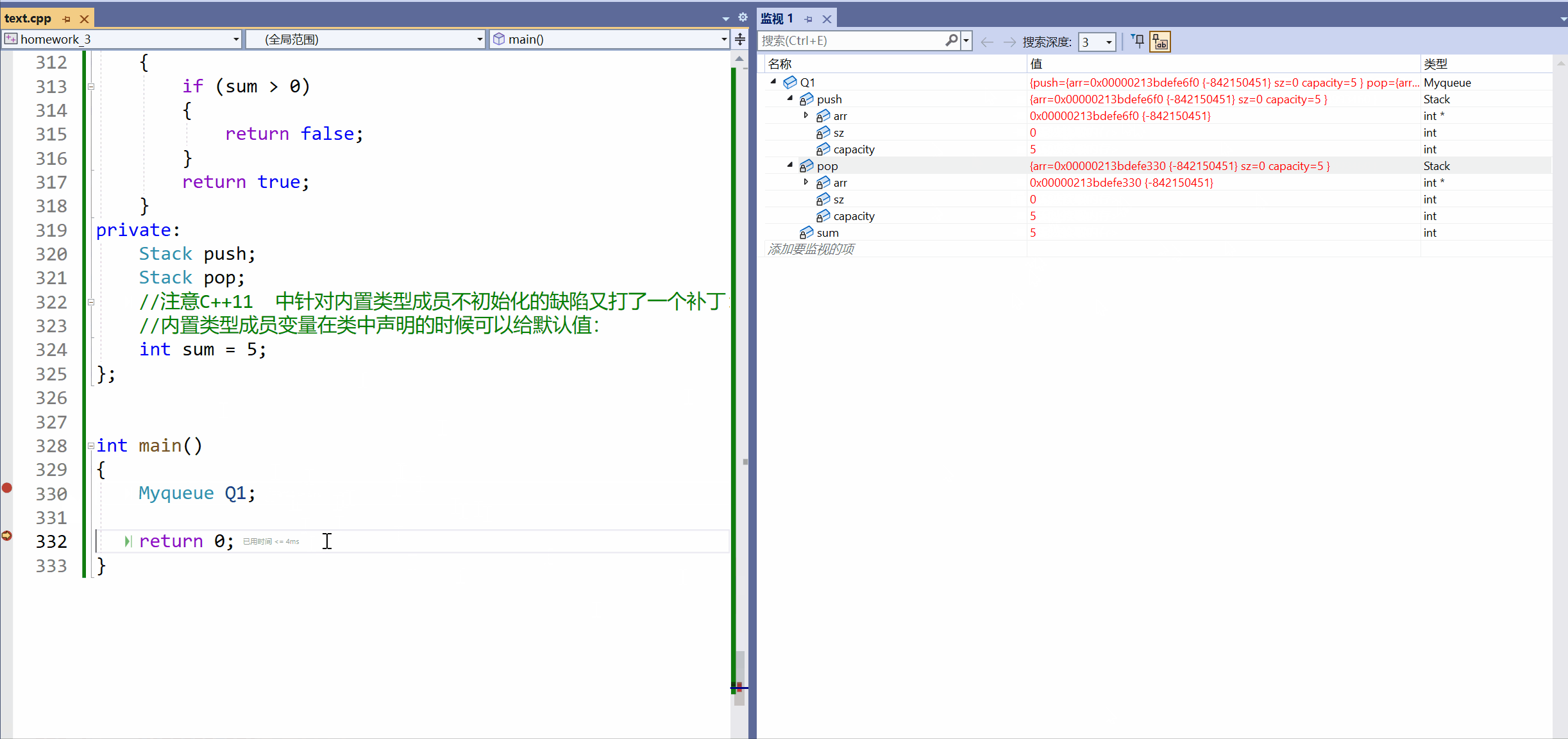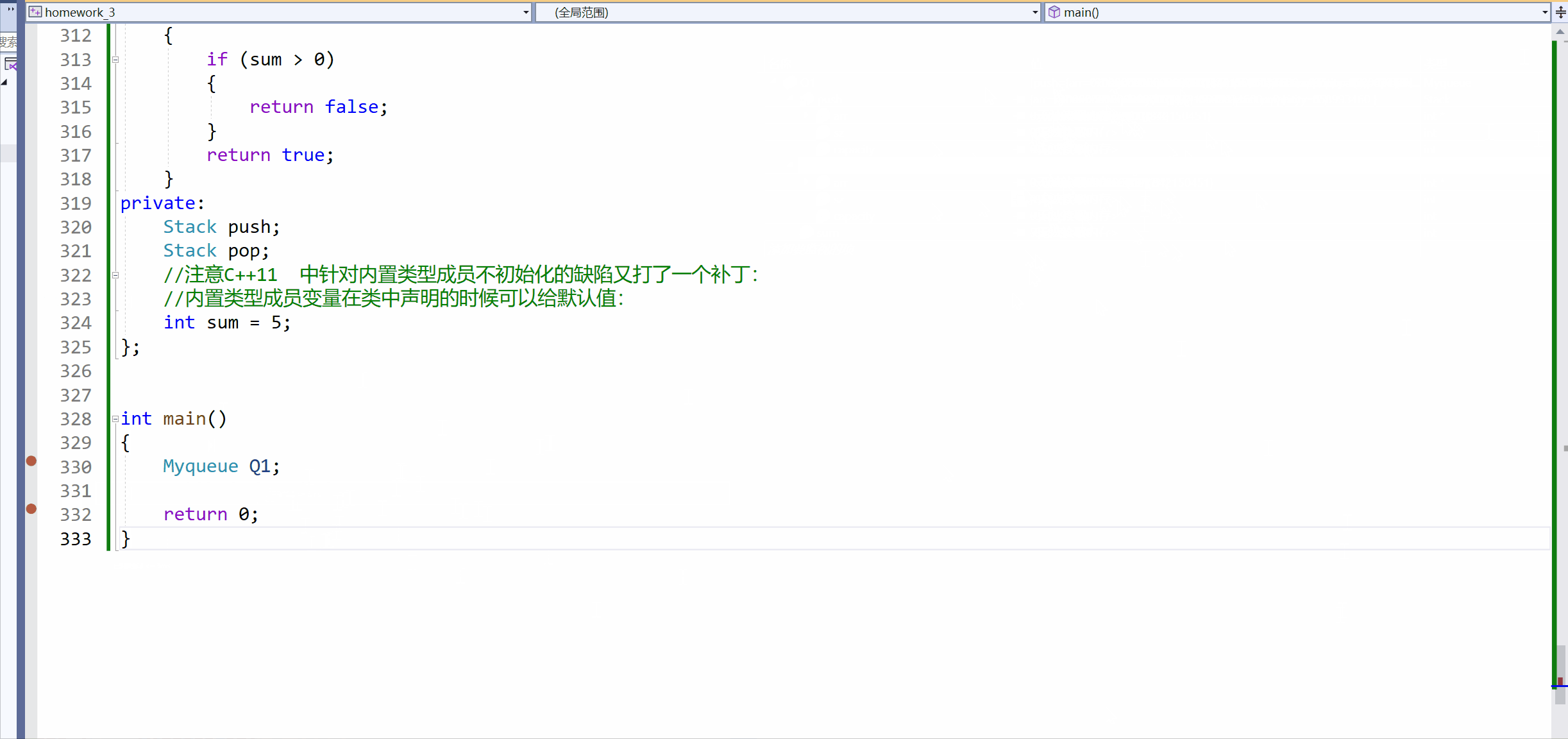
[C++]3.类和对象下(this指针补充)+ 类和对象中构造函数和析构函数。
类和对象下(this指针补充) 类和对象中构造函数和析构函数 一.this补充:1.概念总结:2.两个问题: 二.构造函数和析构函数:一.类的默认构造:1.初始化和清理:2.拷贝复制:3.取…...

OpenLDAP LDIF详解
手把手一步步搭建LDAP服务器并加域 有必要理解的概念LDAPWindows Active Directory 服务器配置安装 OpenLDAP自定义安装修改对象(用户和分组等)修改olcSuffix 和 olcRootDN 属性增加olcRootPW 属性修改olcAccess属性验证新属性值 添加对象(用…...

Leetcode.33 搜索旋转排序数组
题目链接 Leetcode.33 搜索旋转排序数组 mid 题目描述 整数数组 n u m s nums nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前, n u m s nums nums 在预先未知的某个下标 k ( 0 ≤ k < n u m s . l e n g t h )…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...
