Python变量的定义和使用
定义:变量就是计算机内存中存储某些数据的位置的名称
形象理解变量就是一个存放东西的容器,该容器的名字就叫做变量,容器存放的东西就是变量的值
变量的组成:
标识:标识对象所储存的内存地址,使用内置函数id(obj)来获取
类型:表示的是对象的数据类型,使用内置函数type(obj)来获取
值: 表示对象所存储的具体数据,使用print(obj)可以将值进行打印输出
Python中在定义变量之前要先给变量赋值
name = '小明'
其中name就是变量名,=是赋值符号 小明是变量的值
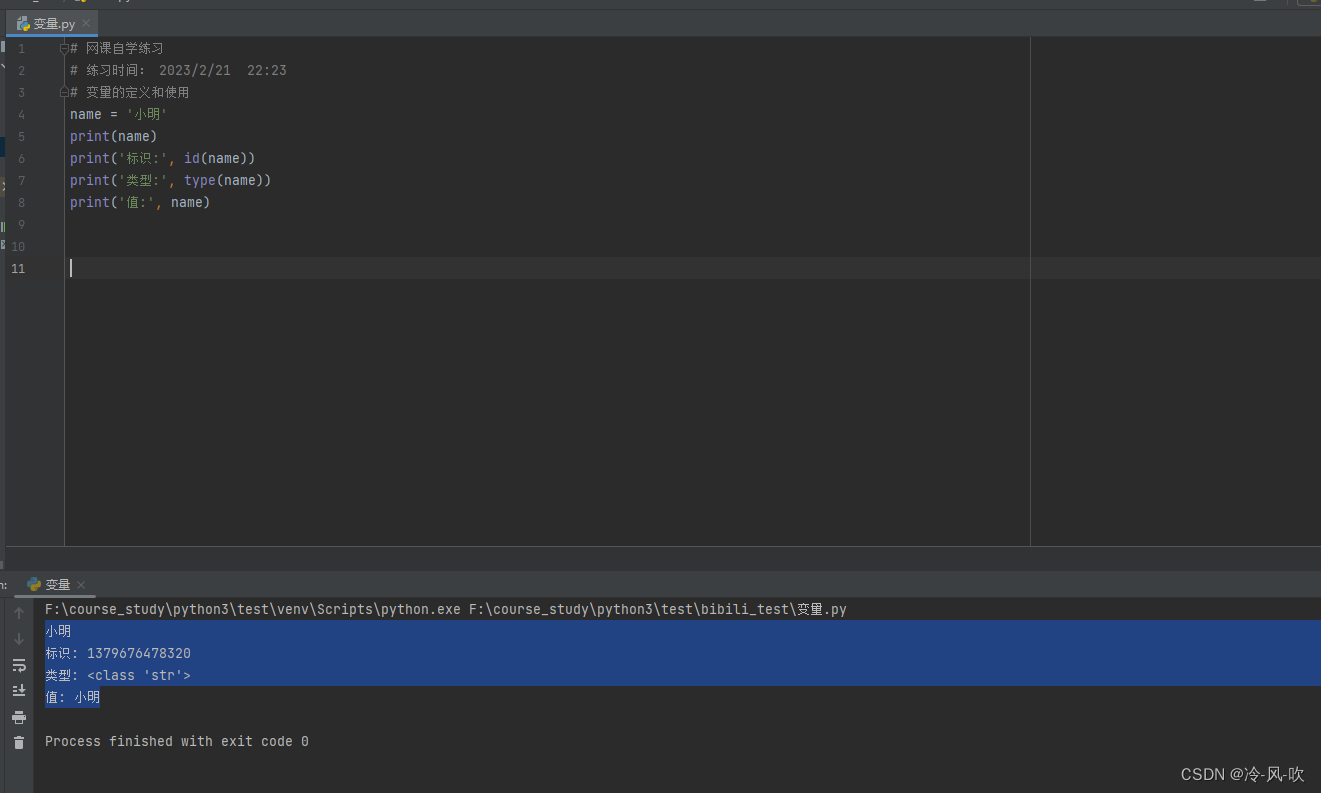
案例如下: name = '小明' print(name) print('标识:', id(name)) print('类型:', type(name)) print('值:', name)输出:
小明
标识: 1379676478320
类型: <class 'str'>
值: 小明
当变量多次赋值之后,变量名会指向新的空间
例如
name = '小明' print(name) name = '小红' print(name)输出:
小明
小红
可以一次定义多个变量,同时给几个变量赋值
l例如语句:a=b=c=d=1 就是定义变量a,b, c,d 并给他们赋值为1
相关文章:
Python变量的定义和使用
定义:变量就是计算机内存中存储某些数据的位置的名称 形象理解变量就是一个存放东西的容器,该容器的名字就叫做变量,容器存放的东西就是变量的值 变量的组成: 标识:标识对象所储存的内存地址,使用内置函数i…...
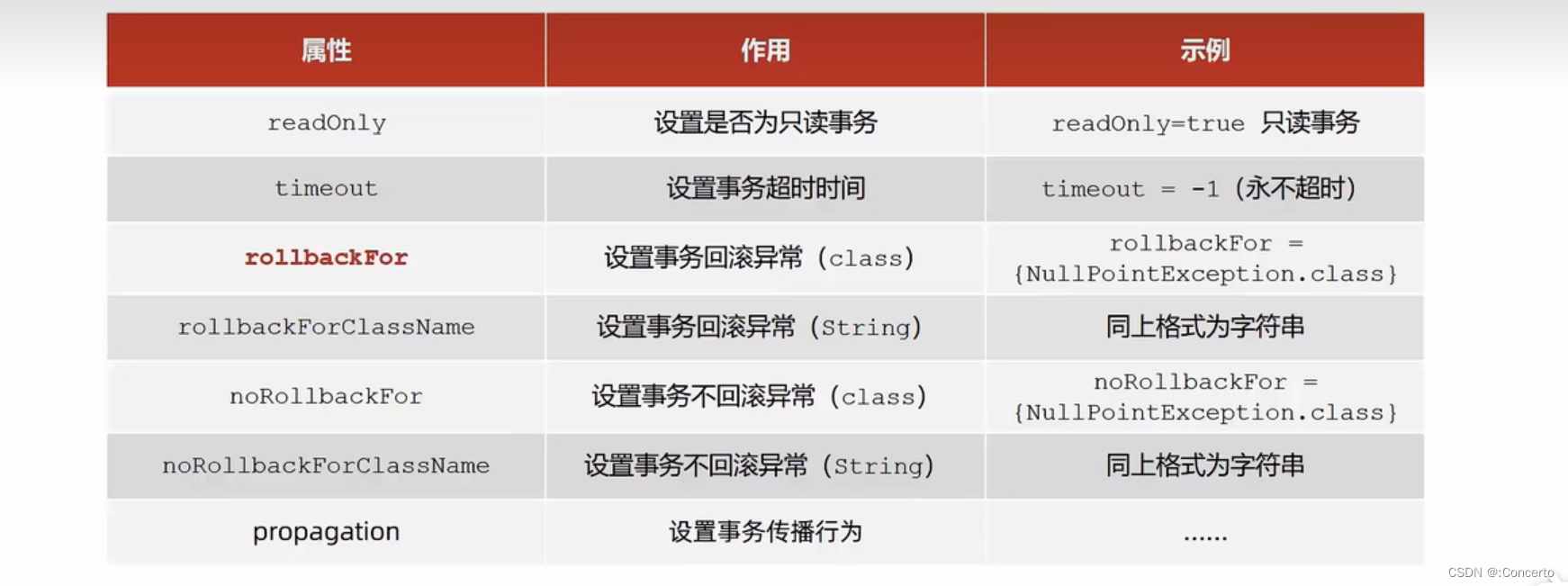
SSM框架-AOP概述、Spring事务
16 spring整合mybatis 16.1 前情代码 实体类 public class Account {private Integer id;private String name;private Double money;public Integer getId() {return id;}public void setId(Integer id) {this.id id;}public String getName() {return name;}public void …...

一文搞定Android Vsync原理简析
屏幕渲染原理"现代计算机之父"冯诺依曼提出了计算机的体系结构: 计算机由运算器,存储器,控制器,输入设备和输出设备构成,每部分各司其职,它们之间通过控制信号进行交互。计算机发展到现在,已经出…...
第八届蓝桥杯省赛 C++ B组 - K 倍区间
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:蓝桥杯题解集合 📝原题地址:K 倍区间 📣专栏定位:为想参加蓝桥杯的小伙伴整理常考算法题解,祝大家…...
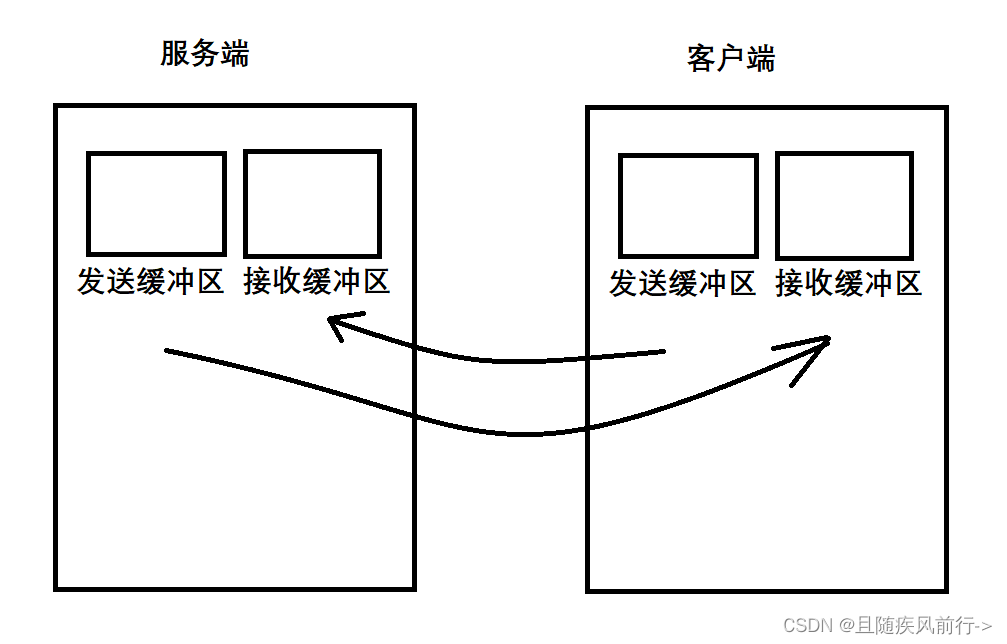
UDP与TCP协议
目录 UDP协议 协议报头 UDP协议特点: 应用场景: TCP TCP协议报头 确认应答机制 理解可靠性 超时重传机制 连接管理机制 三次握手: 四次挥手: 滑动窗口 如何理解缓冲区和滑动窗口? 倘若出现丢包…...

rosbag相关使用工具
文章目录一、 rosbag 导出指定话题生成新rosbag二、 rosbag 导出视频1. 脚本工具源码2. 操作2.1 安装 ffmpeg2.2 导出视频3. 视频截取4. 压缩视频附录:rosbag2video.py 源码一、 rosbag 导出指定话题生成新rosbag rosbag filter 2023-02-25-19-16-01.bag depth.bag…...

数据结构与算法—栈stack
目录 栈 栈的复杂度 空间复杂度O(1) 时间复杂度O(1) 栈的应用 1、栈在函数调用中的应用; 2、栈在求表达式的值的应用: 栈的实现 栈 后进先出,先进后出,只允许在一端插入和删除 从功能上,数组和链表可以代替栈…...

【学习笔记】[ARC150F] Constant Sum Subsequence
第一眼看上去,这道题一点都不套路 第二眼看上去,大概是要考dpdpdp优化,那没事了,除非前面333道题都做完了否则直接做这道题肯定很亏 首先我们要定义一个好的状态。废话 设fsf_{s}fs表示BBB序列的和为sss时,能达到…...

Node.js实现大文件断点续传—浅析
Node.js简介: 当谈论Node.js时,通常指的是一个基于Chrome V8 JavaScript引擎构建的开源、跨平台的JavaScript运行时环境。以下是一些Node.js的内容: 事件驱动编程:Node.js采用了事件驱动的编程范式,这意味着它可以异步…...
Spring Cloud Nacos源码讲解(九)- Nacos客户端本地缓存及故障转移
Nacos客户端本地缓存及故障转移 在Nacos本地缓存的时候有的时候必然会出现一些故障,这些故障就需要进行处理,涉及到的核心类为ServiceInfoHolder和FailoverReactor。 本地缓存有两方面,第一方面是从注册中心获得实例信息会缓存在内存当…...

MySQL知识点小结
事务 进行数据库提交操作时使用事务就是为了保证四大特性,原子性,一致性,隔离性,持久性Durability. 持久性:事务一旦提交,对数据库的改变是永久的. 事务的日志用于保存对数据的更新操作. 这个操作T1事务操作的会发生丢失,因为最后是T2提交的修改,而且T2先进行一次查询,按照A…...
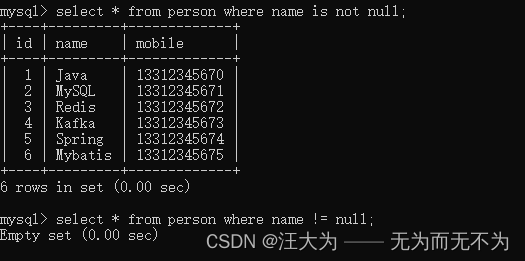
MySQL关于NULL值,常见的几个坑
数据库版本MySQL8。 1.count 函数 觉得 NULL值 不算数 ,所以开发中要避免count的时候丢失数据。 如图所示,以下有7条记录,但是count(name)却只有6条。 为什么丢失数据?因为MySQL的count函数觉得 Null值不算数,就是说…...

OllyDbgqaqazazzAcxsaZ
本文通过吾爱破解论坛上提供的OllyDbg版本为例,讲解该软件的使用方法 F2对鼠标所处的位置打下断点,一般表现为鼠标所属地址位置背景变红F3加载一个可执行程序,进行调试分析,表现为弹出打开文件框F4执行程序到光标处F5缩小还原当前…...

Elasticsearch7.8.0版本进阶——自定义分析器
目录一、自定义分析器的概述二、自定义的分析器的测试示例一、自定义分析器的概述 Elasticsearch 带有一些现成的分析器,然而在分析器上 Elasticsearch 真正的强大之 处在于,你可以通过在一个适合你的特定数据的设置之中组合字符过滤器、分词器、词汇单 …...

spring事务-创建代理对象
用来开启事务的注解EnableTransactionManagement上通过Import导入了TransactionManagementConfigurationSelector组件,TransactionManagementConfigurationSelector类的父类AdviceModeImportSelector实现了ImportSelector接口,因此会调用public final St…...

Linux 配置NFS与autofs自动挂载
目录 配置NFS服务器 安装nfs软件包 配置共享目录 防火墙放行相关服务 配置NFS客户端 autofs自动挂载 配置autofs 配置NFS服务器 nfs主配置文件参数(/etc/exports) 共享目录 允许地址1访问(选项1,选项2) 循序地…...
【编程入门】应用市场(Python版)
背景 前面已输出多个系列: 《十余种编程语言做个计算器》 《十余种编程语言写2048小游戏》 《17种编程语言10种排序算法》 《十余种编程语言写博客系统》 《十余种编程语言写云笔记》 《N种编程语言做个记事本》 目标 为编程初学者打造入门学习项目,使…...

异常信息记录入库
方案介绍 将异常信息放在日志里面,如果磁盘定期清理,会导致很久之前的日志丢失,因此考虑将日志中的异常信息存在表里,方便后期查看定位问题。 由于项目是基于SpringBoot构架的,所以采用AdviceControllerExceptionHand…...

Spring Batch 高级篇-分区步骤
目录 引言 概念 分区器 分区处理器 案例 转视频版 引言 接着上篇:Spring Batch 高级篇-并行步骤了解Spring Batch并行步骤后,接下来一起学习一下Spring Batch 高级功能-分区步骤 概念 分区:有划分,区分意思,在…...
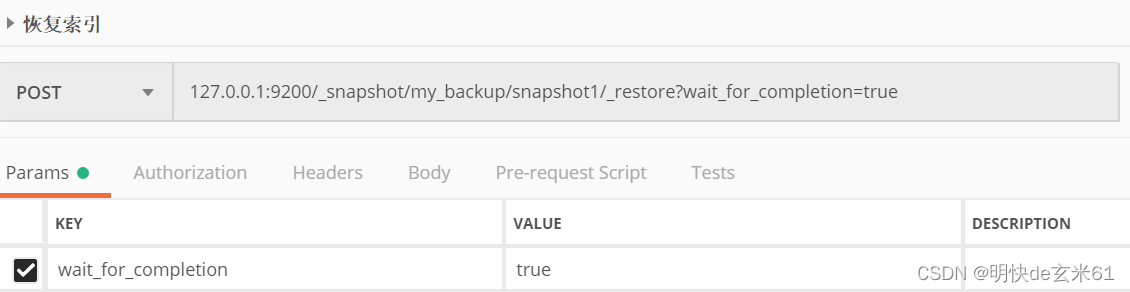
ES数据迁移_snapshot(不需要安装其他软件)
参考文章: 三种常用的 Elasticsearch 数据迁移方案ES基于Snapshot(快照)的数据备份和还原CDH修改ElasticSearch配置文件不生效问题 目录1、更改老ES和新ES的config/elasticsearch.yml2、重启老ES,在老ES执行Postman中创建备份目录…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
