JAVA排序
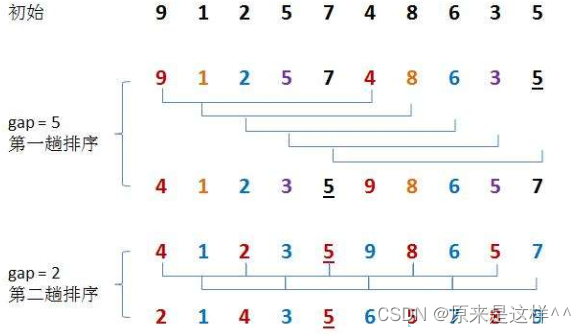
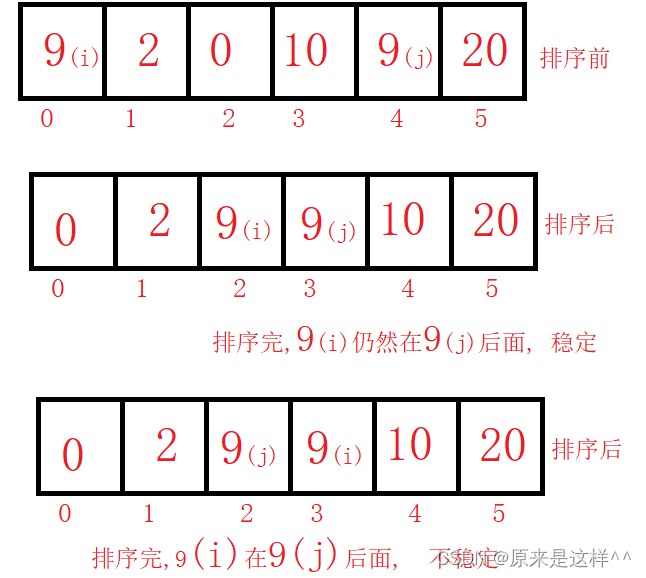
再看各种排序前我们先了解一下什么叫 稳定性
比如一组数据arr[i]下标与arr[j下标]相等,arr[i]在前面,arr[j]在arr[i]后面,排序后这两个数据仍然是arr[i]在arr[j]前面,arr[j]在arr[i]后面,这就叫稳定
插入排序:
优势: 越有序查找速度越快
时间复杂度: O(N^2)
空间复杂度: O(1)
稳定性:稳定
public void insertSort(int[] arr){//i负责引路,j负责把i后面的数据都变得有序for(int i = 1; i < arr.length; i++){for(int j = i - 1; j >= 0; j--){//想想为什么不是arr[j] > arr[i]:因为j会变化if(arr[j] > arr[j+1]){//交换int tmp = arr[j];arr[j] = arr[j+1];arr[j+1] = tmp;}else{break;}}}}
希尔排序:(插入排序的优化)
将所有数据进行分组,先分成许多组,这样每组数据就会变少,在将组的数据排序,
即使时间复杂度是O(N^2)也没事,因为数据少,就算N的平方也没多少
然后逐渐减少组的数量,每组的数据就会变多,但数据越趋近于有序,所以查找速度越快(因为插入排序数据越趋于有序查找速度越快)
最后让 insertSort(arr,1)是为了确保让 希尔排序 排序成功
public void xiErSort(int[] arr){int len = arr.length;//为什么不是while(len >= 0)呢? 反例: len为2时:2 = 2 / 2;会死循环//并且len > 0 说明while(len > 0){//对数据进行分组len = len / 2;//对分组后的数据进行插入排序insertSort(arr,len);}//保证 希尔排序 是有序的insertSort(arr,1);}private void insertSort(int[] arr,int len){for(int i = len; i < arr.length; i++){for(int j = i - len; j >= 0; j = j - len){if(arr[j] > arr[j+len]){//交换int tmp = arr[j];arr[j] = arr[j+len];arr[j+len] = tmp;}else{break;}}}}
问个问题:为何 xiEr方法里的最后要加一段insertSort(arr,1)?
答:为了让希尔排序是彻彻底底有序的,这样虽然看起来和插入排序一样,但因为经过前面的代码数据已经趋于有序,所以最后加个插入排序其实时间复杂度也不高
测试插入排序和希尔排序(插入排序的优化)排序时间对比

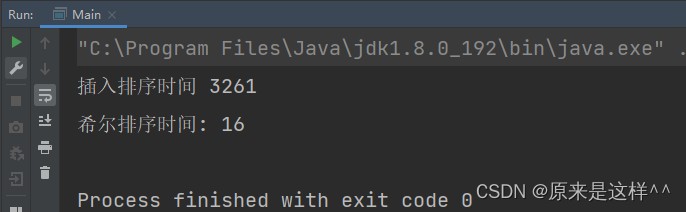
可以看到希尔排序比插入排序快很多
选择排序:
时间复杂度: O(n^2)
空间复杂度: O(1)
稳定性: 不稳定
思路:找到数组里的最小值和最左边i下标交换,如何i++,继续找i后面的最小值然后和i交换,这样就能从小到大排序了
//选择排序public void selectSort(int[] arr){int i = 0;for(i = 0; i < arr.length; i++){int min = i;for(int j = i+1; j < arr.length; j++){//找到数组中最小的数据对应 下标minif(arr[j] < arr[min]){min = j;}}//找到最小值min和数组i下标交换数据int tmp = arr[min];arr[min] = arr[i];arr[i] = tmp;}问个问题:为什么min不写在这里?
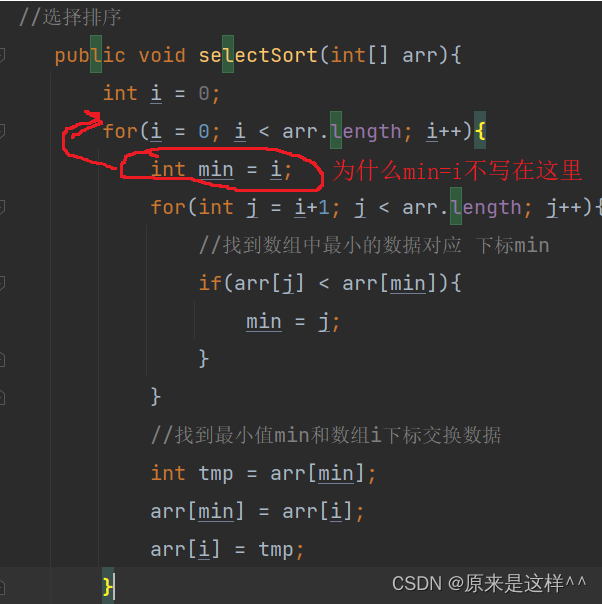
原因是为了让min变量不断变化将数组里的最小值按从小到大顺序排好,放在箭头所指位置就不变化了,也就是说只能将数据放在相同的位置不动
选择排序的优化:
之前是找到最小值就换位置,那我能不能一次找到最小值和最大值再换位置?将最小值换到数据偏左的位置,将最大值放到数据偏右边的位置
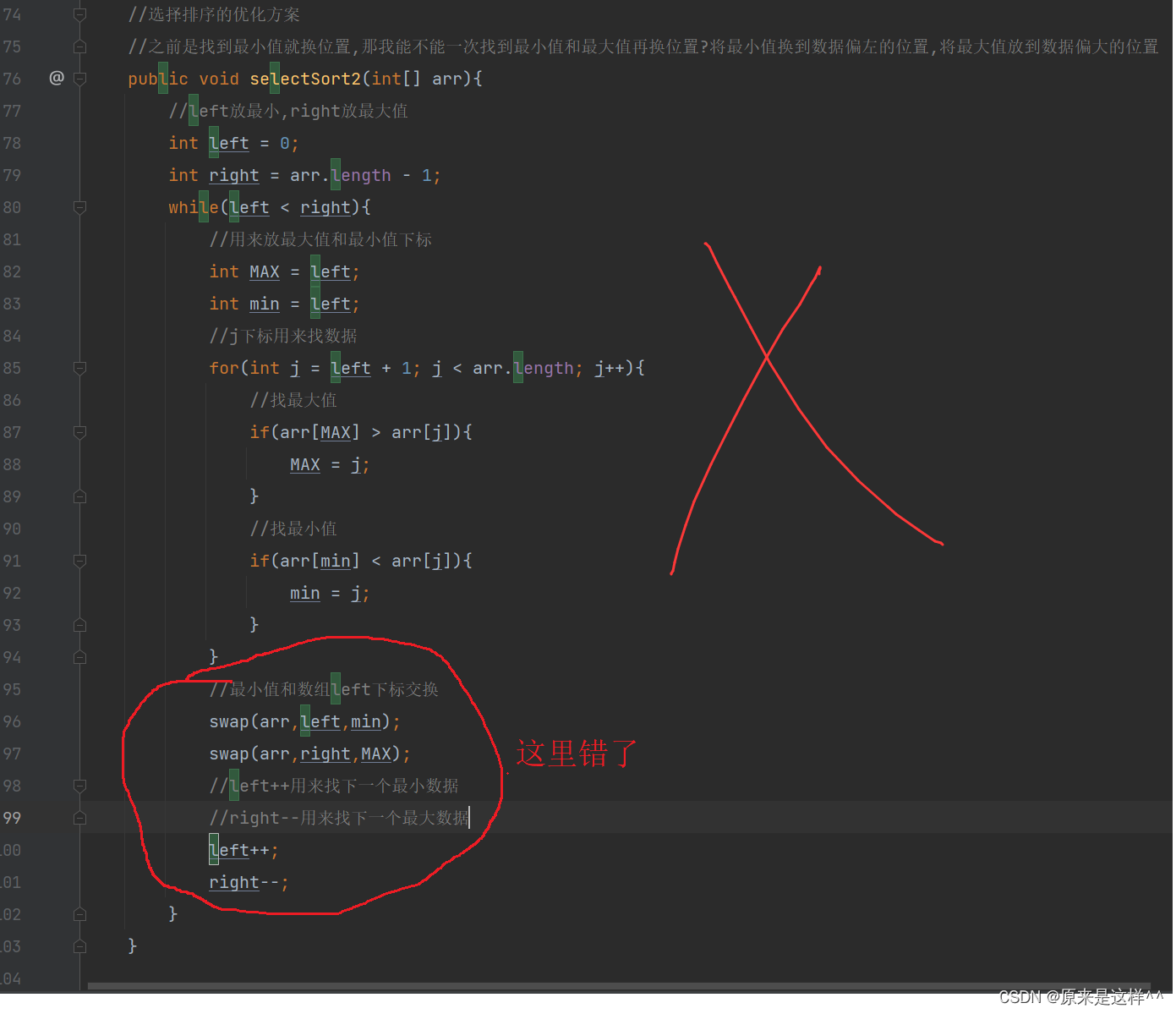

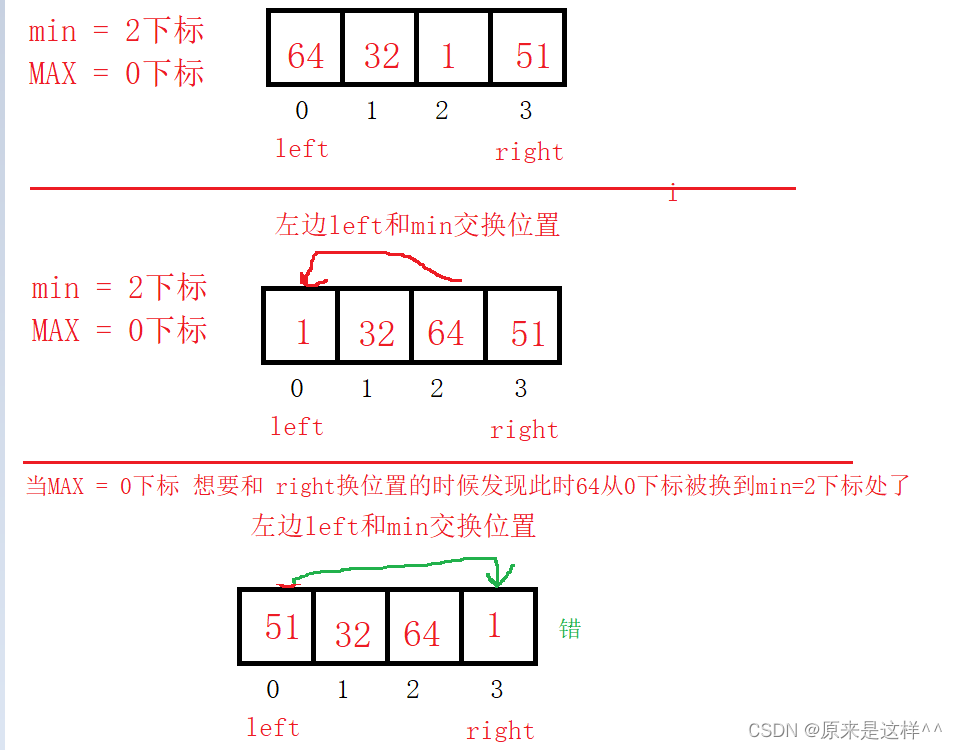
为什么呢?原因是 如果 最大值MAX = left的时候就会把原来的最大值下标移到其它下标处(听懂掌声)
正确的 选择排序优化
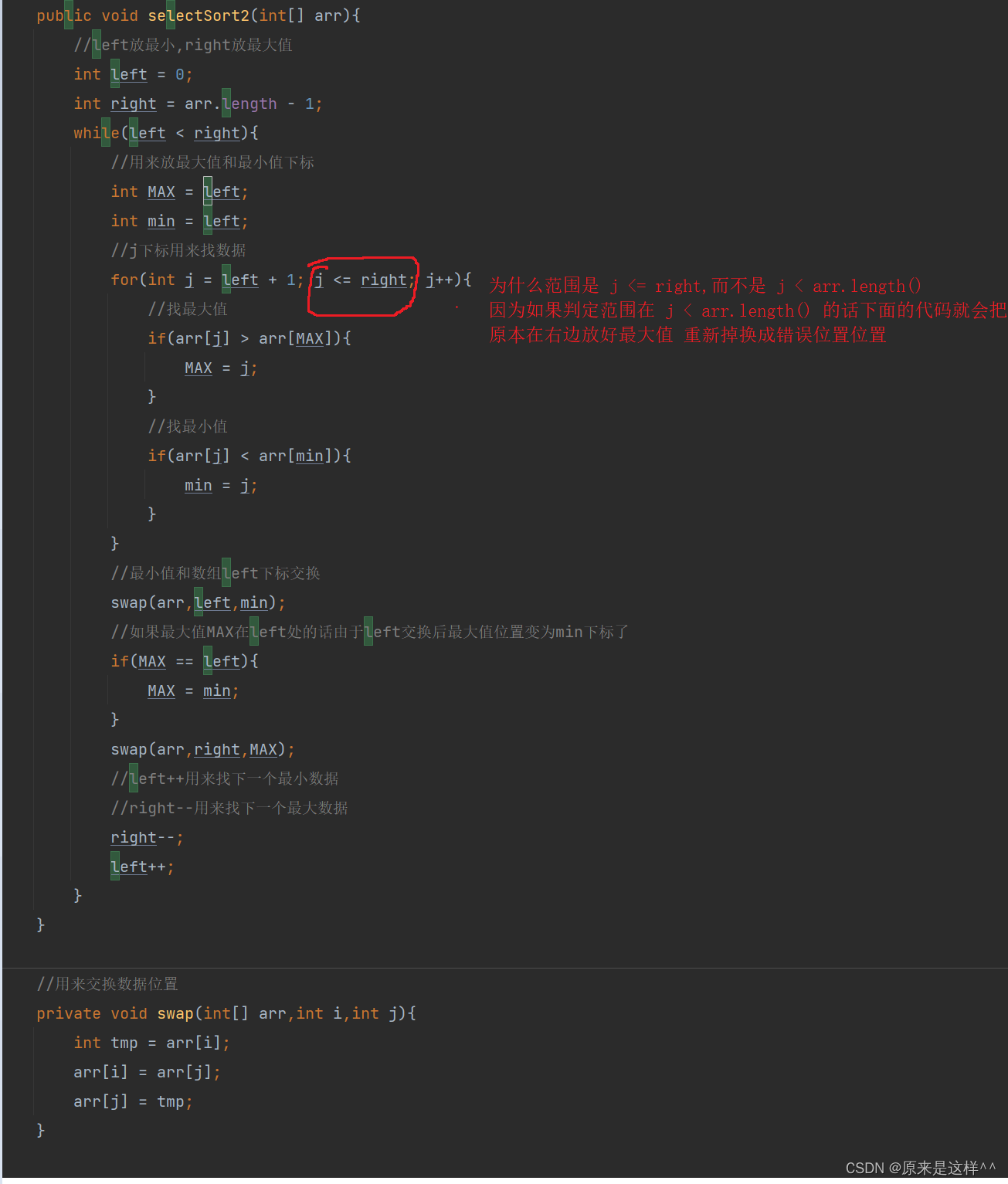
//选择排序的优化方案//之前是找到最小值就换位置,那我能不能一次找到最小值和最大值再换位置?将最小值换到数据偏左的位置,将最大值放到数据偏大的位置public void selectSort2(int[] arr){//left放最小,right放最大值int left = 0;int right = arr.length - 1;while(left < right){//用来放最大值和最小值下标int MAX = left;int min = left;//j下标用来找数据for(int j = left + 1; j <= right; j++){//找最大值if(arr[j] > arr[MAX]){MAX = j;}//找最小值if(arr[j] < arr[min]){min = j;}}//最小值和数组left下标交换swap(arr,left,min);//如果最大值MAX在left处的话由于left交换后最大值位置变为min下标了if(MAX == left){MAX = min;}swap(arr,right,MAX);//left++用来找下一个最小数据//right--用来找下一个最大数据right--;left++;}}//用来交换数据位置private void swap(int[] arr,int i,int j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}为什么范围是 j <= right,而不是 j < arr.length()
因为如果判定范围在 j < arr.length() 的话下面的代码就会把
原本在右边放好最大值 重新掉换成错误位置位置
快速排序(挖坑法:未优化)
时间复杂度O(N*logN)
空间复杂度O(logN)
大体上是找到一个 基准点,基准点的左边得数据都比基准点小,基准点的右边数据都比基准点大
然后递归分成左树和右树
//快速排序(挖坑法:未优化)//为了接口的和其他的一样我们参数就设为int[] arrpublic void quickSort(int[] arr){quickSort_(arr,0,arr.length-1);}public void quickSort_(int[] arr,int left,int right){//为什么是left >= right就结束,而不是left > right呢?//因为当 left == right 就说明 左边或右边只有一个数字呢,一个数字必然是有序的if(left >= right){return;}int index = centreIndex(arr,left,right);//这样 左边 就比基准值index小了, 右边 比基准值大//将数组按基准值的左边划为左树,基准值的右边划分为右树//左边quickSort_(arr,left,index - 1);//右边quickSort_(arr,index+1,right);}//找到基准下标位置public int centreIndex(int[] arr,int left,int right){int tmp = arr[left];while(left < right){//找到右边比基准值小的数while(left < right && arr[right] >= tmp){right--;}//右边遇到比基准值小的,和左边left换位置swap(arr,left,right);//找到左边比基准值大的数while(left < right && arr[left] <= tmp){left++;}//左边遇到比基准值大的,和右边right换位置swap(arr,left,right);}//出到这里说明 left == rightif(left == right){arr[left] = tmp;}return left;}//用来交换数据位置private void swap(int[] arr,int i,int j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}问?为什么红圈圈起来的都使用的是 >=
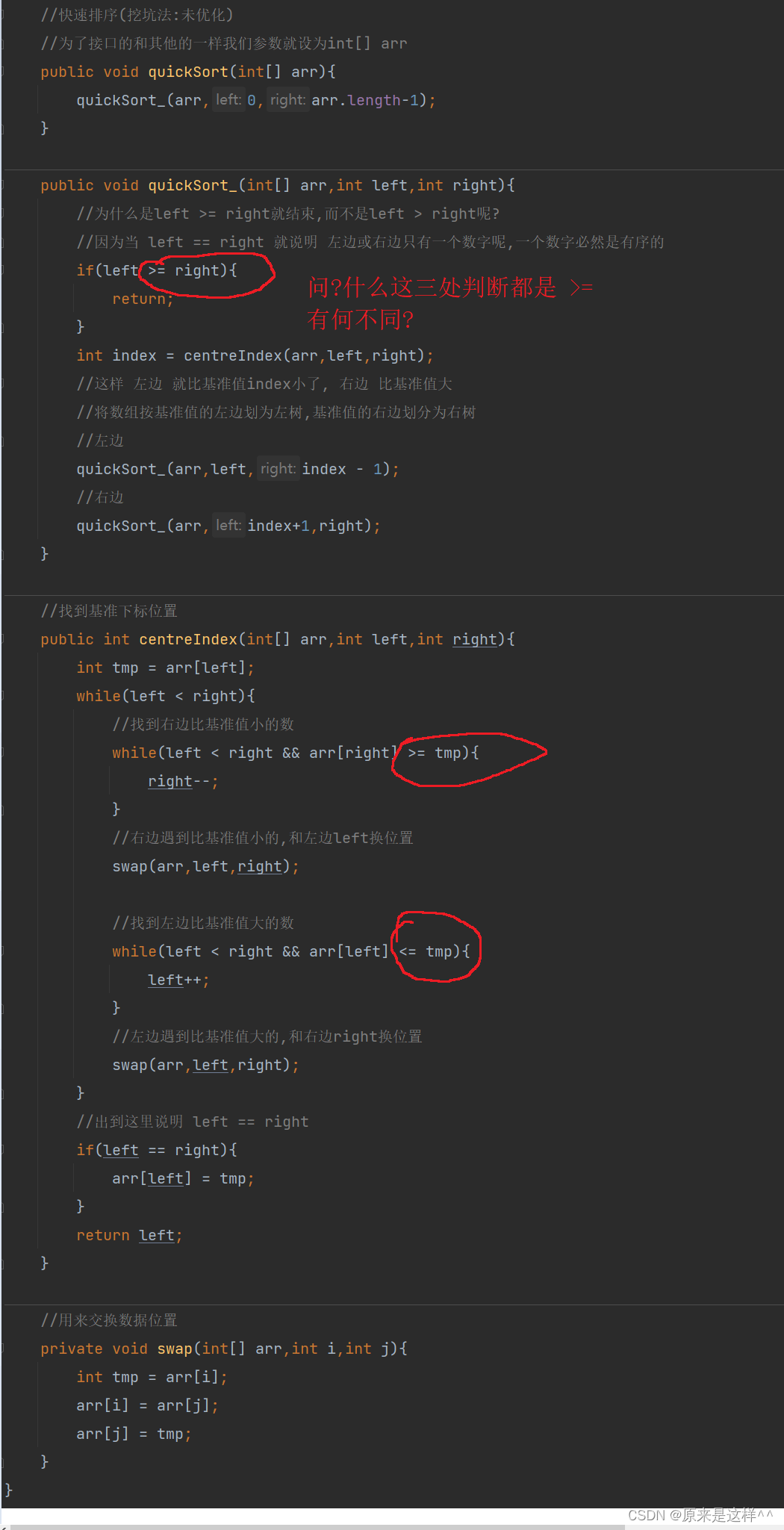
答:第一处if(left >= right) 中 判断条件是 >= 是因为 当left == right的时候说明在递归到最后left == riight的时候说明 只有一个数字,一个数字不管怎么样都是有序的
第二处第三处的while(left < right && arr[left] >= tmp)是为了防止死循环,如果数据像下面数组一样没有>=就死循环了

问:为什么在找基准值方法centreIndex_()里的while(left < right && arr[left] >= tmp)while循环里有while(left < right),原因还是上面那幅图,为了防止数组下标越界
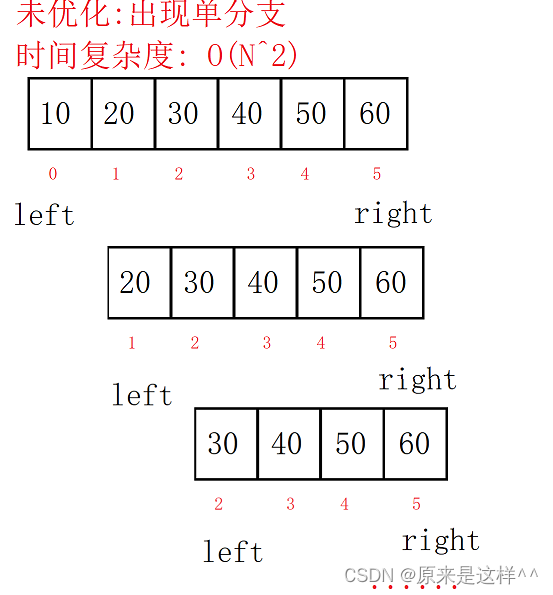
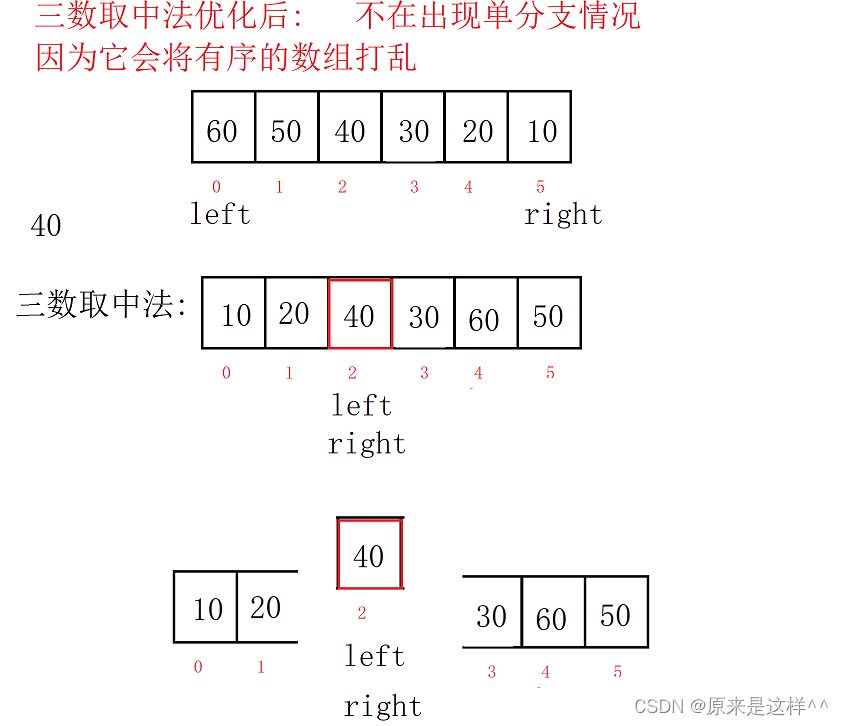
快速排序的优化1
1.为了防止数组里的数据是有序而出现单分支的情况,我们会先使用三数取中的方法将数组里的数据打乱,使得数组里的数据无法有序,从而快速排序也不会出现单分支的情况了
光是左树或右树复杂度是最高的
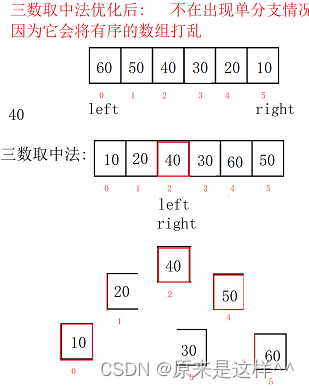
快速排序优化2
1.我们使用快速排序时快到最后发现最后树的节点是最多的,但整体趋近于有序,并且最后一两层就占据了整个数据的60%甚至70%,所以我们可以在快速排序的最后一两层使用 插入排序 的方法来优化, 插入排序的特点就是 数组越有序,插入排序效果越快
//快速查找(挖坑法:优化1)//优化它是单分支的数据public void quickSort2(int[] arr){quickSort_2(arr,0,arr.length - 1);}private void quickSort_2(int[] arr,int left,int right){if(left >= right){return;}//为了防止出现数组有序而出现的 单分支的情况
// 使用 三数去中法int centreIndex = num(arr,left,right);//swap(arr,0,centreIndex)swap(arr,left,centreIndex);//调换完成就不会出现 数组有序而出现的 单分支 的情况啦//找基准值int index = centreIndex2(arr,left,right);//递归左树 和右树quickSort_2(arr,left,index-1);quickSort_2(arr,index+1,right);}//基准值private int centreIndex2(int[] arr,int left,int right){int tmp = arr[left];while(left < right){while(left < right && arr[right] >= tmp){right--;}swap(arr,left,right);while(left <right && arr[left] <= tmp){left++;}swap(arr,left,right);}// left == rightif(left == right) {arr[left] = tmp;}return left;}//三数去中private int num(int[] arr,int left,int right){//取数组最左边,最右边和中间,取中间大小的值int mid = (left+right) / 2;//将三个数放到数组里int[] arrays = new int[3];arrays[0] = arr[left];arrays[1] = arr[mid];arrays[2] = arr[right];//排序Arrays.sort(arrays);if(arrays[1] == arr[left]){return left;}else if(arrays[1] == arr[mid]){return mid;}return right;}//用来交换数据位置private void swap(int[] arr,int i,int j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}//挖坑法的优化(插入排序)private void insertSort2(int[] arr,int left,int right){for(int i = left + 1; i <= right; i++){for(int j = i - 1; j >= left; j--){if(arr[j] > arr[j+1]){//第一个比第二个大,交换int tmp = arr[j];arr[j] = arr[j+1];arr[j+1] = tmp;}}}}优化快速排序需要注意的点
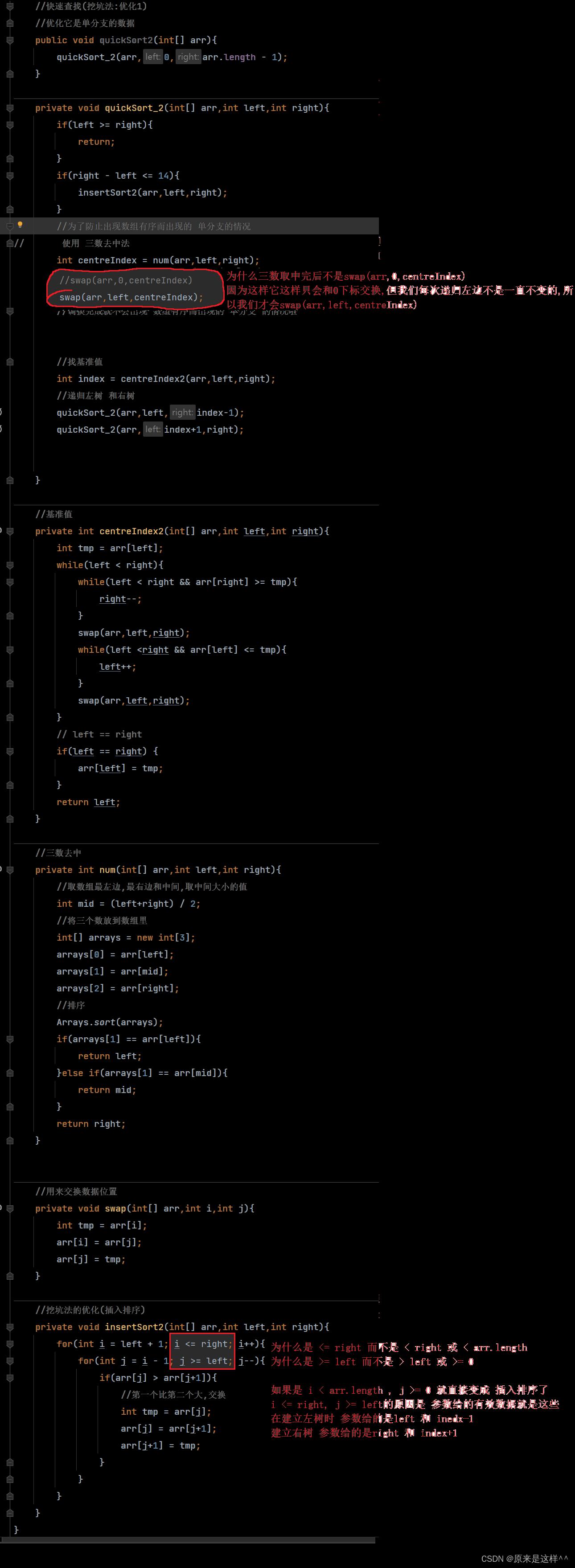
使用双指针法进行快速排序
思路:和普通快速排序的思路差不多,先找基准值,基准值的左边小于基准值,基准值的右边大于基准值,然后使用递归直到left >= right时结束,双指针快速排序主要与普通快排就是使用了双指针的方法进行找基准值
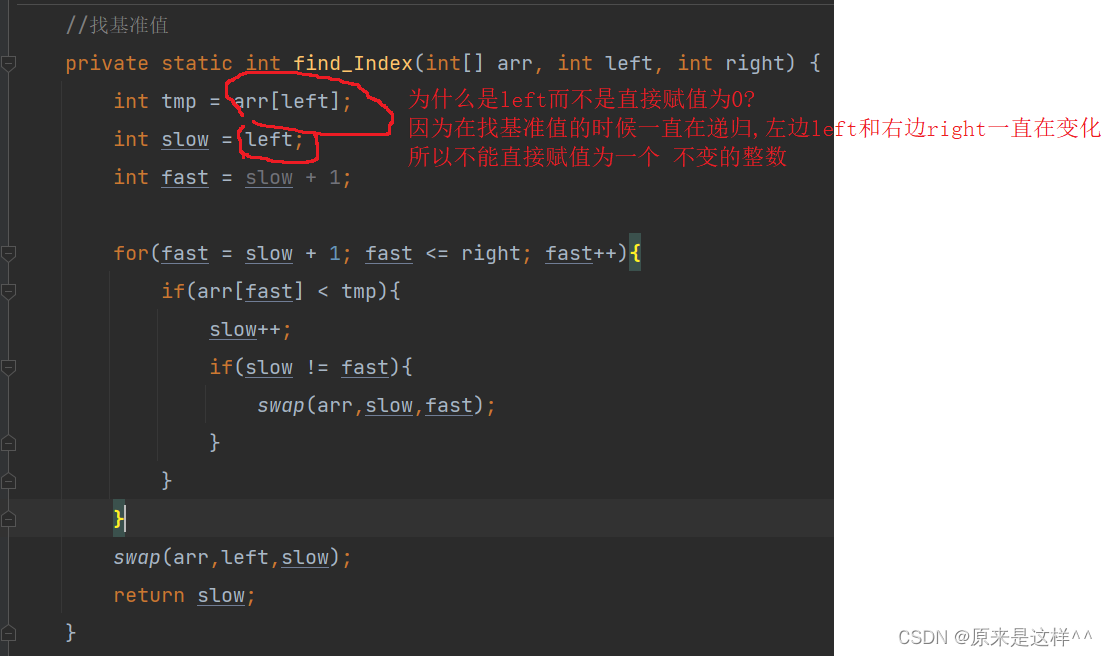
public static void double_index(int[] arr){if(arr.length == 0){return;}double_Index(arr,0,arr.length-1);}private static void double_Index(int[] arr, int left, int right) {if(left >= right){return;}//找基准int index = find_Index(arr,left,right);double_Index(arr,left,index - 1);double_Index(arr,index+1,right);}//找基准值private static int find_Index(int[] arr, int left, int right) {int tmp = arr[left];int slow = left;int fast = slow + 1;for(fast = slow + 1; fast <= right; fast++){if(arr[fast] < tmp){slow++;if(slow != fast){swap(arr,slow,fast);}}}swap(arr,left,slow);return slow;}private static void swap(int[] arr, int slow, int fast) {int tmp = arr[slow];arr[slow] = arr[fast];arr[fast] = tmp;}双指针主要看这几行代码
slow指针永远指向数组里比tmp小的最后一个数据,而fast指针则是数组里找比tmp小的数据
堆排序
先根据数组创建成一个堆
从小到大排序就创建成大根堆,从大到小排序就创建成小根堆
创建完堆后就将 堆顶元素 和 堆的末尾元素 调换位置,这样堆顶元素(最大的)就放到最后,然后在将调换的堆顶元素重新建成大根堆,在继续调换,这样就会形成一个从小到大排序的数组
public static void prioritySort(int[] arr){if(arr.length == 0){return;}//首先先拿这个数组用来创建一个堆//从小到大排序的话就创建 大根堆//从大到小排序的话就创建 小根堆for (int father = (arr.length - 1) / 2; father >= 0; father--) {create(arr,father,arr.length);}int len = arr.length;//排序while(len > 0){//交换int tmp = arr[0];arr[0] = arr[len-1];arr[len-1] = tmp;len--;//重新将换了的堆顶元素变为 大根堆create(arr,0,len);
// len--;}}//从小到大排序(创建大根堆)private static void create(int[] arr,int father,int len){int child = (father * 2)+1;while(child < len){//找到最大的孩子节点if(child+1 < len && arr[child+1] > arr[child]){child++;}//这样child指向的就是最大的孩子节点了//最大的孩子节点 和 父亲节点比较if(arr[child] > arr[father]){//交换int tmp = arr[father];arr[father] = arr[child];arr[child] = tmp;father = child;child = (father * 2)+1;
// child = father;
// father = (child-1)/2;}else{break;}}}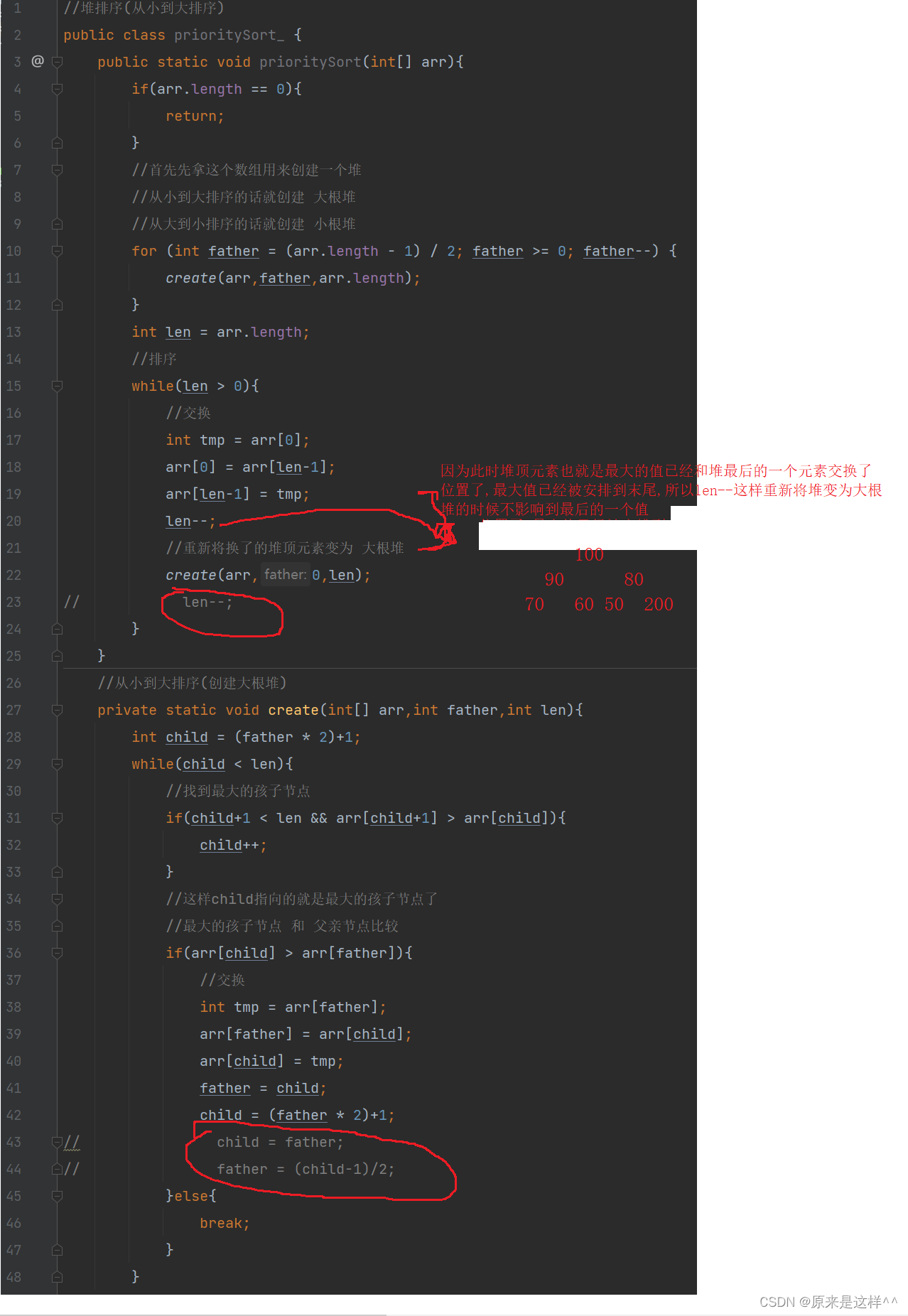
冒泡排序:感觉没什么好讲的这个:一般不会用它
//冒泡排序(优化)public static void Sort2(int[] arr){for(int i = 0; i < arr.length; i++){boolean judge = false;for(int j = 0; j < arr.length-1-i; j++){if(arr[j] > arr[j+1]){//交换int tmp = arr[j];arr[j] = arr[j+1];arr[j+1] = tmp;judge = true;}//else {// break//}}if(!judge){return;}}}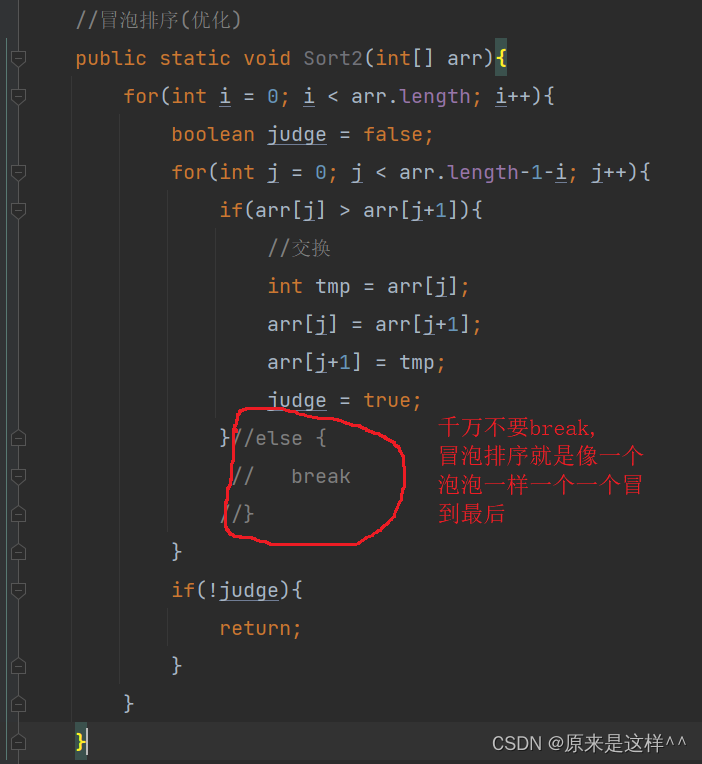
相关文章:

JAVA排序
再看各种排序前我们先了解一下什么叫 稳定性 比如一组数据arr[i]下标与arr[j下标]相等,arr[i]在前面,arr[j]在arr[i]后面,排序后这两个数据仍然是arr[i]在arr[j]前面,arr[j]在arr[i]后面,这就叫稳定 插入排序: 优势: 越有序查找速度越快 时间复杂度: O(N^2) 空间复…...

opencalib中lidar2camera安装记录
目录 一、opencalib安装 二、lidar2camera的安装 三、测试运行 四、出现过的问题 一、opencalib安装 代码地址:https://github.com/PJLab-ADG/SensorsCalibration/blob/master/README.md # pull docker image sudo docker pull scllovewkf/opencalib:v1 # Aft…...

整个自动驾驶小车001:概述
材料: 1,树梅派4b,作为主控,这个东西有linux系统,方便 2,HC-S104超声波模块,我有多个,不少于4个,我可以前后左右四个方向都搞一个 3,l298n模块,…...

windows本地搭建mmlspark分布式机器平台流程
文章目录 windows本地搭建mmlspark分布式机器平台流程安装环境pyspark环境spark环境java环境hadoop环境1.修改hadoop配置文件下的jdk地址为自己的实际地址2.修改bin文件离线环境jar包环境1mmlsprk第三方包jar包环境2参考代码我有话说其他问题记录概要参考文献windows本地搭建mm…...

深入探究 Next.js 中的 getServerSideProps 和 getStaticProps 用法及区别
引言: Next.js 是一个流行的 React 框架,它提供了许多强大的功能来简化服务器渲染(SSR)和静态生成(SSG)的过程。其中,getServerSideProps 和 getStaticProps 是两个重要的函数,用于在…...

餐饮业如何高效经营?赶紧闭眼抄这个方法!
在现代社会,餐饮业已经成为人们日常生活中不可或缺的一部分。为了提高食堂运营效率,满足不断增长的客户需求,智慧收银系统应运而生。 智慧收银系统帮助食堂业主更好地理解其客户,提高服务质量,优化库存管理,…...
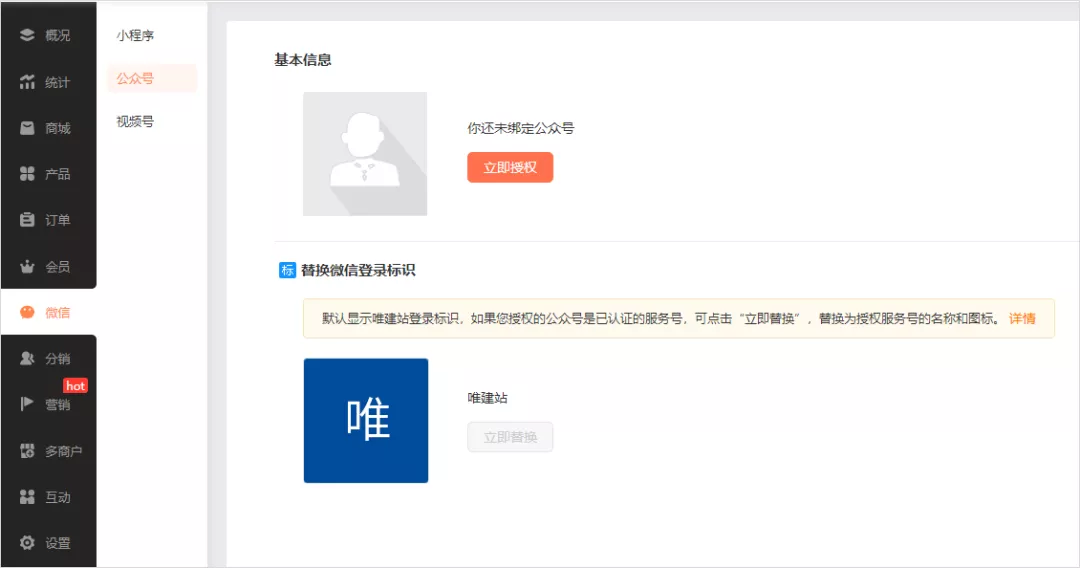
餐饮外卖小程序商城的作用是什么
随着互联网及线上餐饮的发展趋势,行业洗牌正在加速,并且对餐饮连锁门店提出更高要求,餐饮数字化转型加快,积极发展线上经营是不少餐饮商家的首选。这其中,餐饮外卖商城成为很多餐饮品牌的线上经营品牌,也是…...
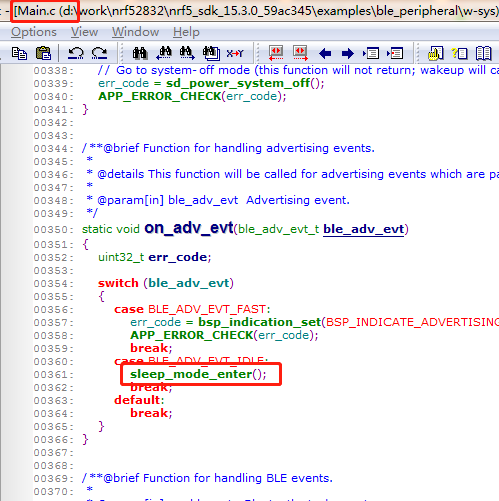
nRF52832 SDK15.3.0 基于ble_app_uart demo FreeRTOS移植
参考资料:Nrf52832 freeOS系统移植_nrf5283操作系统-CSDN博客 这里把移植经验记录下来,供有需要的同学参考,有不对的地方也请大家批评指正。 把FreeRTOS移植到 nRF5_SDK_15.3.0_59ac345\examples\ble_peripheral\ble_app_uart工程ÿ…...
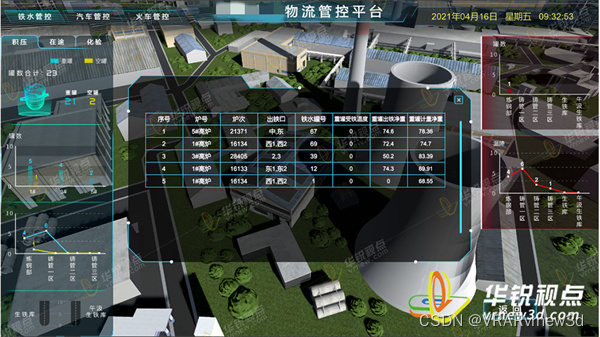
电厂数据可视化三维大屏展示平台加强企业安全防范
园区可视化大屏是一种新型的信息化手段,能够将园区内各项数据信息以图像的形式直观呈现在大屏幕上,便于管理员和员工进行实时监控、分析和决策。本文将从以下几个方面介绍园区可视化大屏的作用和应用。 VR数字孪生园区系统是通过将实际园区的各种数据和信…...

2246: 【区赛】【宁波32届小学生】最佳交换
目录 题目描述 输入 输出 样例输入 样例输出 提示 代码 题目描述 星星小朋友和 N-1 个小伙伴一起玩了一上午的纸牌游戏,星星总是能赢,气焰嚣张, 小伙伴们决定出道纸牌问题难倒星星,让他别再狂妄自大了,问题是这…...

Java面试记录
文章目录 1、final关键字2、synchronized关键字(1)synchronized的功能:(2)synchronized的底层实现原理: 3、Java中线程同步的实现方法(1). 使用synchronized关键字:&…...

【数据库】聚集函数
聚集函数 聚集函数一览AVG() 函数COUNT() 函数MAX() 函数MIN() 函数SUM() 函数 组合聚集函数 聚集函数一览 我们需要汇总数据而不是实际检索,此时我们使用聚集函数进行处理; 聚集函数一览表如下: 函数说明AVG()返回平均值COUNT()返回数量总…...

【单元测试】--编写单元测试
一、编写第一个单元测试 编写第一个单元测试通常包括以下步骤。以下示例以C#和NUnit为例: 创建测试项目: 在Visual Studio中,创建一个新的Class Library项目,这将是你的单元测试项目。在解决方案资源管理器中,右键点…...

ES(elasticsearch) - 三种姿势进行分页查询
1. from size 浅分页 "浅"分页可以理解为简单意义上的分页。它的原理很简单,就是查询前20条数据,然后截断前10条,只返回10-20的数据。这样其实白白浪费了前10条的查询。 GET test_dev/_search {"query": {"bool&…...
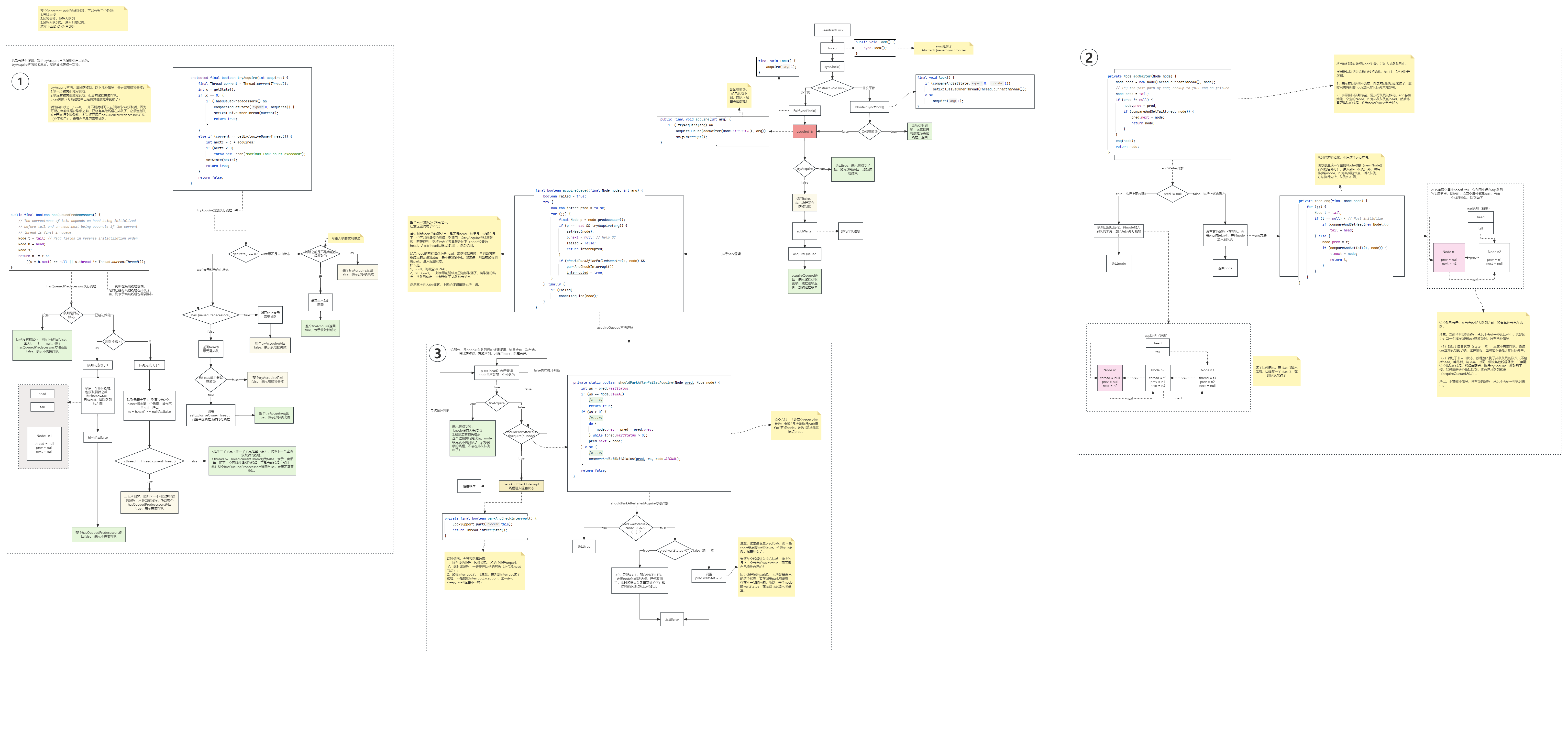
AQS是什么?AbstractQueuedSynchronizer之AQS原理及源码深度分析
文章目录 一、AQS概述1、什么是AQS2、技术解释3、基本原理4、AQS为什么这么重要 二、AQS数据结构1、AQS的结构2、ReentrantLock与AbstractQueuedSynchronizer3、AQS的state变量4、AQS的队列5、AQS的Node(1)Node的waitStatus(2)属性…...
)
【数据库】函数处理(文本处理函数、日期和时间处理函数、数值处理函数)
函数处理数据 算术运算函数文本处理函数日期和时间处理函数数值处理函数 算术运算 操作符说明加-减*乘/除 e . g . e.g. e.g. 列出 Orders 表中所有每项物品的 id,数量 quantity,单价 item_price,总价 expanded_price(数量 * 单价…...

GEE案例——一个完整的火灾监测案例dNBR差异化归一化烧毁指数
差异化归一化烧毁指数 dNBR是"差异化归一化烧毁指数"的缩写。它是一种用于评估卫星图像中烧毁区域严重程度的遥感指数。dNBR值通过将火灾前的归一化烧毁指数(NBR)减去火灾后的NBR来计算得出。该指数常用于野火监测和评估。 dNBR(差异化归一化烧毁指数)是一种用…...

计算机算法分析与设计(20)---回溯法(0-1背包问题)
文章目录 1. 题目描述2. 算法思路3. 例题分析4. 代码编写 1. 题目描述 对于给定的 n n n 个物品,第 i i i 个物品的重量为 W i W_i Wi,价值为 V i V_i Vi,对于一个最多能装重量 c c c 的背包,应该如何选择放入包中的物品…...

什么是IO多路复用?Redis中对于IO多路复用的应用?
IO多路复用是一种高效的IO处理方式,它允许一个进程同时监控多个文件描述符(包括套接字、管道等),并在有数据可读或可写时进行相应的处理。这种机制可以大大提高系统的并发处理能力,减少资源的占用和浪费。 在Redis中&…...

NanoPC-T4 RK3399:DTS之io-domain,FAN
前言: 之后所有改动均是基于rk3399-evb.dts修改以满足NanoPC-T4功能正常。 NanoPC-T4开发板上有一片散热风扇,本章将讲述使风扇正常工作起来的多种方法。 一:硬件分析 GPIO4_C6/PWM1:实际控制风扇引脚,GPIO与PWM复用 输入高电平1:FAN2pin电路导通,风扇转动 输入低电…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...