【考研数学】数学“背诵”手册 | 需要记忆且容易遗忘的知识点
文章目录
- 引言
- 一、高数
- 常见泰勒展开
- n n n 阶导数公式
- 多元微分函数连续、可微、连续可偏导之间的关系
- 多元函数极值
- 无条件极值
- 条件极值
- 三角函数的积分性质
- 华里士公式( “点火”公式 )
- 特殊性质
- 原函数与被积函数的奇偶性结论
- 球坐标变换公式
- 二、
- 写在最后
引言
复习到后期,去做到前面内容的题目时,有一些需要记忆的结论就比较模糊,比如微分方程的特解形式、施密特正交、各种分布的概率密度等等。我便把这些模糊的点都记录下来了,整理在一起,方便随时查阅
一、高数
常见泰勒展开
基本形式: f ( x ) = ∑ n = 0 ∞ f ( n ) ( x 0 ) n ! ( x − x 0 ) n . f(x)=\sum_{n=0}^\infty \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n. f(x)=n=0∑∞n!f(n)(x0)(x−x0)n. 常见展开式: e x = x n n ! = 1 + x + 1 2 x 2 + ⋯ + 1 n ! x n + ⋯ , − ∞ < x < + ∞ . \pmb{e^x}= \frac{x^n}{n!}=1+x+\frac{1}{2}x^2+\cdots+\frac{1}{n!}x^n+\cdots,-\infty<x<+\infty. ex=n!xn=1+x+21x2+⋯+n!1xn+⋯,−∞<x<+∞. ln ( 1 + x ) = x − 1 2 x 2 + 1 3 x 3 + ⋯ + ( − 1 ) n − 1 x n n + ⋯ , − 1 < x ≤ 1. \ln(1+x)=x-\frac{1}{2}x^2+\frac{1}{3}x^3+\cdots+(-1)^{n-1}\frac{x^n}{n}+\cdots,-1<x\leq1. ln(1+x)=x−21x2+31x3+⋯+(−1)n−1nxn+⋯,−1<x≤1. sin x = x − 1 3 ! x 3 + 1 5 ! x 5 + ⋯ + ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! + ⋯ , − ∞ < x < + ∞ . \pmb{\sin x}=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5+\cdots+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+\cdots,-\infty<x<+\infty. sinx=x−3!1x3+5!1x5+⋯+(−1)n(2n+1)!x2n+1+⋯,−∞<x<+∞. cos x = 1 − 1 2 ! x 2 + 1 4 ! x 4 + ⋯ + ( − 1 ) n x 2 n ( 2 n ) ! + ⋯ , − ∞ < x < + ∞ . \cos x=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4+\cdots+(-1)^{n}\frac{x^{2n}}{(2n)!}+\cdots,-\infty<x<+\infty. cosx=1−2!1x2+4!1x4+⋯+(−1)n(2n)!x2n+⋯,−∞<x<+∞. 1 1 + x = 1 − x + x 2 + ⋯ + ( − 1 ) n x n + ⋯ , − 1 < x < 1. \frac{1}{1+x}=1-x+x^2+\cdots+(-1)^nx^n+\cdots,-1<x<1. 1+x1=1−x+x2+⋯+(−1)nxn+⋯,−1<x<1. 1 1 − x = 1 + x + x 2 + ⋯ + x n + ⋯ , − 1 < x < 1. \pmb{\frac{1}{1-x}}=1+x+x^2+\cdots+x^n+\cdots,-1<x<1. 1−x1=1+x+x2+⋯+xn+⋯,−1<x<1.
n n n 阶导数公式
分数 1 / ( a x + b ) 1/(ax+b) 1/(ax+b) 的 n n n 阶导数: ( 1 a x + b ) ( n ) = ( − 1 ) n a n n ! ( a x + b ) n + 1 \big(\frac{1}{ax+b}\big)^{(n)}=(-1)^n\frac{a^nn!}{(ax+b)^{n+1}} (ax+b1)(n)=(−1)n(ax+b)n+1ann! ( sin x ) ( n ) = sin ( x + n π 2 ) , ( cos x ) ( n ) = cos ( x + n π 2 ) (\sin{x})^{(n)}=\sin{(x+\frac{n\pi}{2})},(\cos{x})^{(n)}=\cos{(x+\frac{n\pi}{2})} (sinx)(n)=sin(x+2nπ),(cosx)(n)=cos(x+2nπ)
多元微分函数连续、可微、连续可偏导之间的关系

多元函数极值
无条件极值

条件极值

三角函数的积分性质
华里士公式( “点火”公式 )
首先是在区间 [ 0 , π / 2 ] [0,\pi/2] [0,π/2] 上 sin , cos \sin,\cos sin,cos 可以互换,即 ∫ 0 π / 2 f ( sin x ) d x = ∫ 0 π / 2 f ( cos x ) d x \int_0^{\pi/2}f(\sin x)dx=\int_0^{\pi/2}f(\cos x)dx ∫0π/2f(sinx)dx=∫0π/2f(cosx)dx 特别地,有华里士公式(点火公式): I n = ∫ 0 π / 2 ( sin x ) n d x = ∫ 0 π / 2 ( cos x ) n d x = n − 1 n I n − 2 , I 0 = π 2 , I 1 = 1. I_n=\int_0^{\pi/2}(\sin x)^ndx=\int_0^{\pi/2}(\cos x)^ndx=\frac{n-1}{n}I_{n-2},I_0=\frac{\pi}{2},I_1=1. In=∫0π/2(sinx)ndx=∫0π/2(cosx)ndx=nn−1In−2,I0=2π,I1=1. 可以推广到更大的区间,在 [ 0 , π ] [0,\pi] [0,π] 上,由于 sin x \sin x sinx 均为正,因此直接点火,乘个 2 就行。 ∫ 0 π ( sin x ) n d x = 2 ∫ 0 π / 2 ( sin x ) n d x . \int_0^{\pi}(\sin x)^ndx=2\int_0^{\pi/2}(\sin x)^ndx. ∫0π(sinx)ndx=2∫0π/2(sinx)ndx. cos x \cos x cosx 由于一半区间为负,因此奇数次和偶数次,奇数次为 0 (可以记忆为奇函数对称为 0 ),偶数次同样是乘 2 。 ∫ 0 π ( cos x ) n d x = 2 ∫ 0 π / 2 ( cos x ) n d x \int_0^{\pi}(\cos x)^ndx=2\int_0^{\pi/2}(\cos x)^ndx ∫0π(cosx)ndx=2∫0π/2(cosx)ndx 对于在区间 [ 0 , 2 π ] [0,2\pi] [0,2π] 上, sin , cos \sin,\cos sin,cos 均有正有负,因此奇数次为 0 ,偶数次乘一个 4 。 ∫ 0 2 π ( sin x ) n d x = ∫ 0 2 π ( cos x ) n d x = 4 ∫ 0 π / 2 ( sin x ) n d x . \int_0^{2\pi}(\sin x)^ndx=\int_0^{2\pi}(\cos x)^ndx=4\int_0^{\pi/2}(\sin x)^ndx. ∫02π(sinx)ndx=∫02π(cosx)ndx=4∫0π/2(sinx)ndx.
特殊性质
在 [ 0 , π ] [0,\pi] [0,π] 上可以降到 [ 0 , π / 2 ] [0,\pi/2] [0,π/2] 上;证明方法为拆区间,令 t = x − π / 2 t=x-\pi/2 t=x−π/2 ,把后半部分换掉。 ∫ 0 π f ( sin x ) d x = 2 ∫ 0 π / 2 f ( sin x ) d x , t h e n w e h a v e , ∫ 0 π / 2 f ( sin x ) d x = ∫ π / 2 π f ( sin x ) d x . \int_0^{\pi}f(\sin x)dx=2\int_0^{\pi/2}f(\sin x)dx,then\space we \space have,\int_0^{\pi/2}f(\sin x)dx=\int_{\pi/2}^{\pi}f(\sin x)dx. ∫0πf(sinx)dx=2∫0π/2f(sinx)dx,then we have,∫0π/2f(sinx)dx=∫π/2πf(sinx)dx. 多一个 x x x 可以提到积分外面来,即 ∫ 0 π x f ( sin x ) d x = π 2 ∫ 0 π f ( sin x ) d x = π ∫ 0 π / 2 f ( sin x ) d x . \int_0^{\pi}xf(\sin x)dx=\frac{\pi}{2}\int_0^{\pi}f(\sin x)dx=\pi\int_0^{\pi/2}f(\sin x)dx. ∫0πxf(sinx)dx=2π∫0πf(sinx)dx=π∫0π/2f(sinx)dx. 证明方法为令 t = x − π t=x-\pi t=x−π 。
原函数与被积函数的奇偶性结论
- f ( x ) f(x) f(x) 为奇函数可推出 ∫ a x f ( t ) d t \int_a^x f(t)dt ∫axf(t)dt 为偶函数。
- f ( x ) f(x) f(x) 为偶函数,不能得到 ∫ a x f ( t ) d t \int_a^x f(t)dt ∫axf(t)dt 为奇函数,但可以得到 ∫ 0 x f ( t ) d t \int_0^x f(t)dt ∫0xf(t)dt 为奇函数。
- ∫ a x f ( x ) d x \int_a^x f(x)dx ∫axf(x)dx 为奇/偶函数,一定可以推得 f ( x ) f(x) f(x) 为相反的奇偶性。
- ∫ a x f ( x ) d x \int_a^x f(x)dx ∫axf(x)dx 为周期函数,一定可以推得 f ( x ) f(x) f(x) 也为周期函数,反之不一定。
球坐标变换公式
r r r 表示几何体上一点到原点距离,从原点引一条射线看范围; θ \theta θ 表示 r r r 在 x O y xOy xOy 平面的投影直线与 x x x 轴正向的夹角,范围是 [ 0 , 2 π ] [0,2\pi] [0,2π]; φ \varphi φ 表示和 z z z 轴正向夹角,范围是 [ 0 , π ] [0,\pi] [0,π] ,想象喇叭开花。
变换公式为 { x = r cos θ sin φ y = r sin θ sin φ z = r cos φ , d x d y d z = r 2 sin φ d r d θ d φ . \begin{cases} x=r\cos\theta \sin\varphi\\ y=r\sin \theta \sin\varphi \\ z=r\cos\varphi\end{cases},dxdydz=r^2\sin\varphi \space drd\theta d\varphi. ⎩ ⎨ ⎧x=rcosθsinφy=rsinθsinφz=rcosφ,dxdydz=r2sinφ drdθdφ.
二、
写在最后
相关文章:

【考研数学】数学“背诵”手册 | 需要记忆且容易遗忘的知识点
文章目录 引言一、高数常见泰勒展开 n n n 阶导数公式多元微分函数连续、可微、连续可偏导之间的关系多元函数极值无条件极值条件极值 三角函数的积分性质华里士公式( “点火”公式 )特殊性质 原函数与被积函数的奇偶性结论球坐标变换公式 二、写在最后 …...
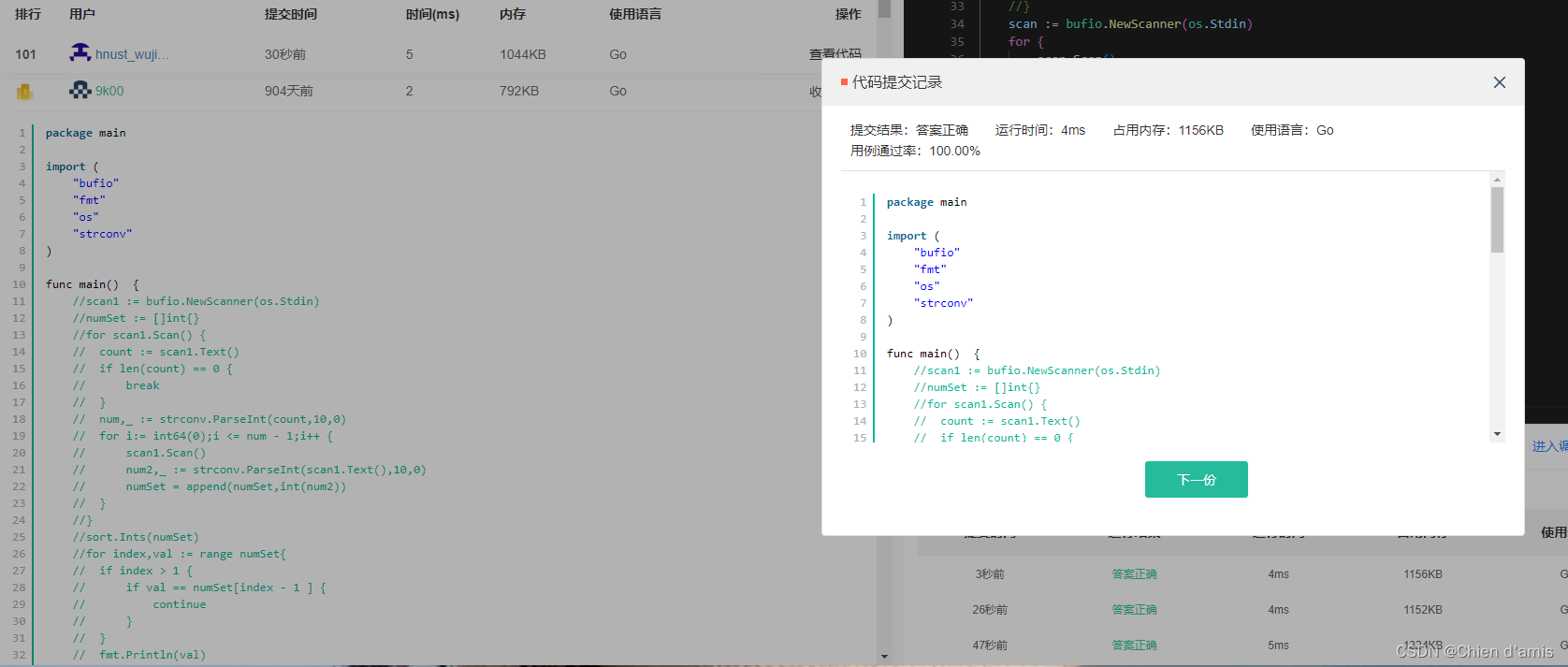
HJ3 明明的随机数
牛客网:HJ3 明明的随机数 https://www.nowcoder.com/practice/3245215fffb84b7b81285493eae92ff0?tpId37&tqId21226&ru/exam/oj 使用Go语言解题,最简单的方式: 解题一: // 运行时间:5ms 占用内存:…...
如何恢复u盘删除文件?2023最新分享四种方法恢复文件
U盘上删除的文件怎么恢复?使用U盘存储文件是非常方便的,例如:在办公的时候,会使用U盘来存储网络上查找到的资料、产品说明等。在学习的时候,会使用U盘来存储教育机构分享的教学视频、重点知识等。而随着U盘存储文件的概…...

8.稳定性专题
1. anr https://code84.com/303466.html 一句话,规定的时间没有干完要干的事,就会发生anrsystem_anr场景 input 5sservice 前台20s 后台60scontentprivider超市 比较少见 原因 主线程耗时 复杂layout iobinder对端block子线程同步锁blockbinder被占满导…...

基于51单片机的四种波形信号发生器仿真设计(仿真+程序源码+设计说明书+讲解视频)
本设计 基于51单片机信号发生器仿真设计 (仿真程序源码设计说明书讲解视频) 仿真原版本:proteus 7.8 程序编译器:keil 4/keil 5 编程语言:C语言 设计编号:S0015 这里写目录标题 基于51单片机信号发生…...
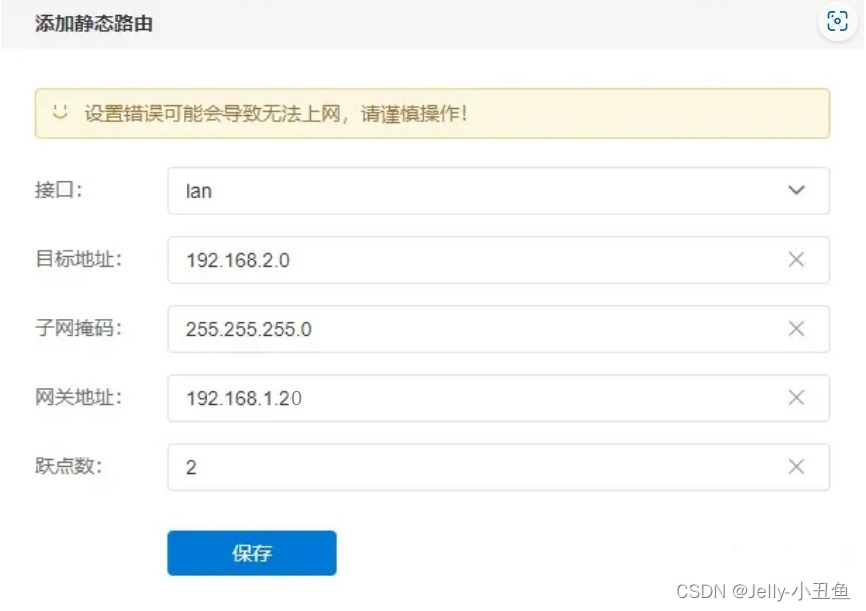
不同网段的IP怎么互通
最近在整理工作的时候发现一个不同网段无法互通的问题,就是我们大家熟知的一级路由和二级路由无法互通的问题。由于需要记录整个过程的完整性,这里也需要详细记录下整个过程,明白的人不用看,可以直接跳过,到解决方法去…...

C#序列化与反序列化详解
在我们深入探时C#序列化和反序列化,之前我们先要明白什么是序列化,它又称串行化,是.ET运行时环境用来支持用户定义 类型的流化的机制。序列化就是把一个对象保存到一个文件或数据库字段中去,反序列化就是在适当的时候把这个文件再…...
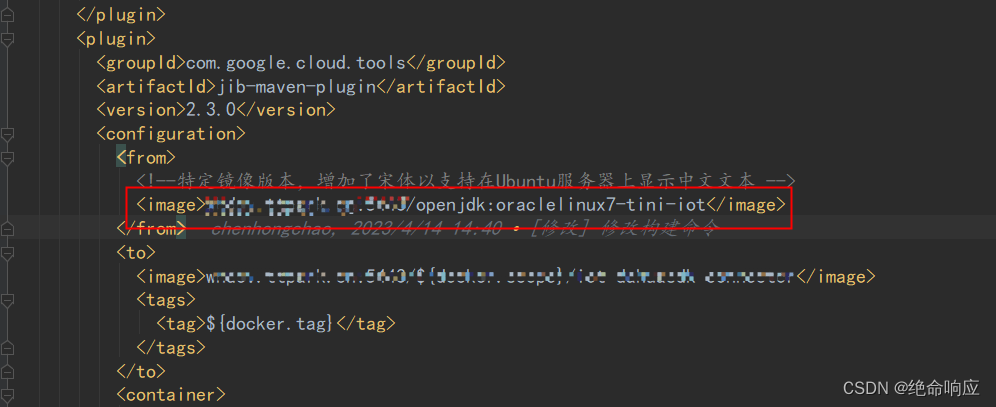
如何在k8s的Java服务镜像(Linux)中设置中文字体
问题描述:服务是基于springboot的Java服务,在项目上是通过Maven的谷歌插件打包,再由k8s部署的。k8s的镜像就是一个Java服务,Java服务用到了中文字体。 解决这个问题首先需要搞定镜像字体的问题。有很多类似的解决方案,…...

CT 扫描的 3D 图像分类-预测肺炎的存在
介绍 此示例将展示构建 3D 卷积神经网络 (CNN) 所需的步骤,以预测计算机断层扫描 (CT) 扫描中是否存在病毒性肺炎。2D CNN 通常用于处理 RGB 图像(3 通道)。3D CNN 就是 3D 的等价物:它以 3D 体积或一系列 2D 帧(例如 CT 扫描中的切片)作为输入,3D CNN 是学习体积数据表…...

整合管理案例题分析
本文摘自江山老师文档 五个过程 制定项目章程 1.没有写项目章程,没有颁布 2.项目经理自己颁布项目章程 3.项目经理修改项目章程 4.项目章程授权不够,项目经理没有权限,下面的人不听话 5.项目章程的内容不完整 制定项目管理计划 1.项目…...

mysql4
创建表并插入数据: 字段名 数据类型 主键 外键 非空 唯一 自增 id INT 是 否 是 是 否 primary key name VARCHAR(50) 否 否 是 否 否 not null glass VARCHAR(50) 否 否 是 否 否 not nullsch 表内容 id name glass 1 xiaommg glass 1 2 xiaojun …...
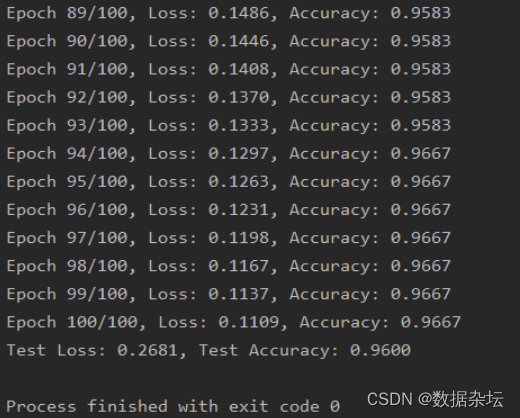
Python深度学习实战-基于tensorflow原生代码搭建BP神经网络实现分类任务(附源码和实现效果)
实现功能 前面两篇文章分别介绍了两种搭建神经网络模型的方法,一种是基于tensorflow的keras框架,另一种是继承父类自定义class类,本篇文章将编写原生代码搭建BP神经网络。 实现代码 import tensorflow as tf from sklearn.datasets import…...

PDF 文档处理:使用 Java 对比 PDF 找出内容差异
不论是在团队写作还是在个人工作中,PDF 文档往往会经过多次修订和更新。掌握 PDF 文档内容的变化对于管理文档有极大的帮助。通过对比 PDF 文档,用户可以快速找出文档增加、删除和修改的内容,更好地了解文档的演变过程,轻松地管理…...

压敏电阻有哪些原理?|深圳比创达电子EMC
压敏电阻是一种金属氧化物陶瓷半导体电阻器。它以氧化锌(ZnO)为基料,加入多种(一般5~10种)其它添加剂,经压制成坯体,高温烧结,成为具有晶界特性的多晶半导体陶瓷组件。氧化锌压敏电阻器的微观结构如下图1所示。 氧化锌…...

【计算机网络笔记】Web应用之HTTP协议(涉及HTTP连接类型和HTTP消息格式)
系列文章目录 什么是计算机网络? 什么是网络协议? 计算机网络的结构 数据交换之电路交换 数据交换之报文交换和分组交换 分组交换 vs 电路交换 计算机网络性能(1)——速率、带宽、延迟 计算机网络性能(2)…...
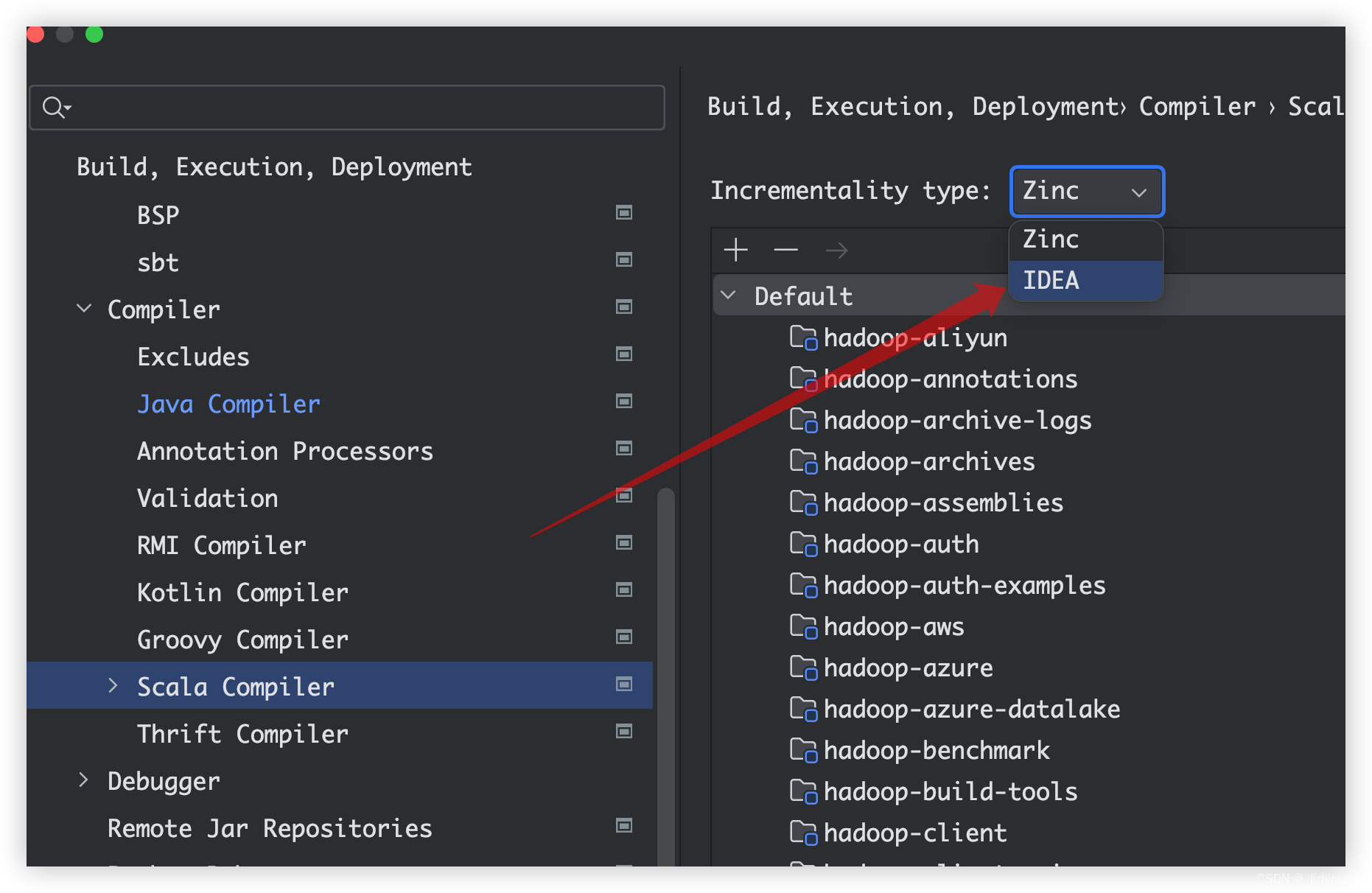
IDEA 2023.2.2 使用 Scala 编译报错 No scalac found to compile scala sources
一、问题 scala: No scalac found to compile scala sources 官网 Bug 链接 二、临时解决方案 Incrementality Type 先变成 IDEA 类型 Please go to Settings > Build, Execution, Deployment > Compiler > Scala Compiler and change the Incrementality type to …...

C51--PWN-舵机控制
PWM开发sg90舵机 1、简介 PWM(pulse width modulation)是脉冲宽度调制缩写。 通过对一系列脉冲的宽度进行调制,等效出所需要的波形(包含形状以及幅值)。对模拟信号电平进行数字编码,通过调节占空比的变化来…...

electron27+react18集成搭建跨平台应用|electron窗口多开
基于Electron27集成React18创建一个桌面端exe程序。 electron27-vite4-react18基于electron27结合vite4构建工具快速创建react18跨端应用实践。 版本列表 "vite": "^4.4.5" "react": "^18.2.0" "electron": "^27.0.1&…...
【k8s】kubeadm安装k8s集群
一、环境部署 master192.168.88.10docker、kubeadm、kubelet、kubectl、flannelnode01192.168.88.20docker、kubeadm、kubelet、kubectl、flannelnode02192.168.88.30docker、kubeadm、kubelet、kubectl、flannelhub.lp.com192.168.88.40 docker、docker-compose harbor-offli…...
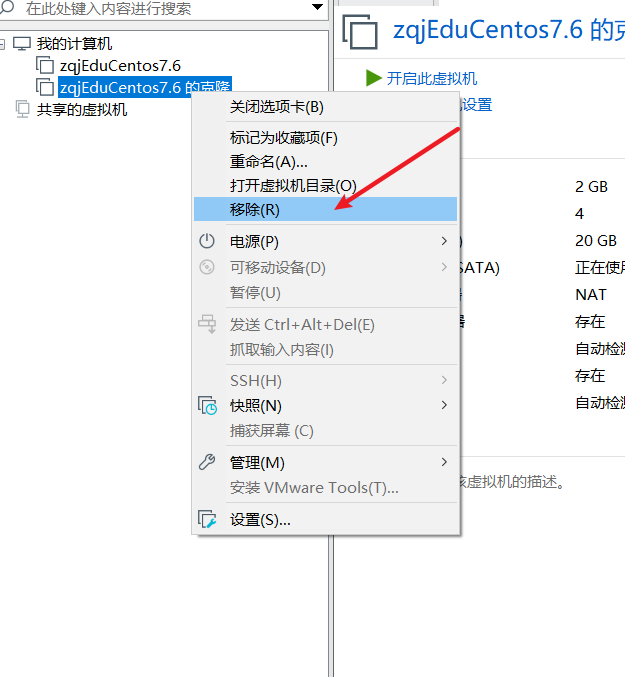
三、虚拟机的迁移和删除
虚拟机的本质就是文件(放在文件夹的)。因此虚拟机的迁移很方便,可以把安装好的虚拟系统这个文件夹整体拷贝或者剪切到另外的位置使用。删除也很简单,使用vmware进行移除,再点菜单->从磁盘删除即可,或者手动删除虚拟系统对应的文…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
