图的应用3.0-----拓扑排序
目录
前言
AOE网
1.相关概念
2.AOE网特征
拓扑排序
1.基本概念
2.方法步骤
3.拓扑排序的应用
拓扑排序代码实现
1.邻接矩阵的代码
2.邻接表代码
前言
今天我们学习图的应用----拓扑排序,说到排序,你们是不是会想到冒泡排序,插入排序,快速排序等等排序方法?但是拓扑排序跟这些不一样,拓扑排序是属于图的一种遍历算法,不属于用于纯数字排序,那什么是拓扑排序呢?下面就一起来看看吧!
AOE网
1.相关概念
有向无环图常用来描述一个工程或系统的进行过程。(通常把计划、施工、生产、程序流程等当成是一个工程
一个工程可以分为若干个子工程,只要完成了这些子工程(活动),就可以导致整个工程的完成。

AOV网
用一个有向图表示一个工程的各子工程及其相互制约的关系,其中以顶点表示活动,弧表示活动之间的优先制约关系,称这种有向图为顶点表示活动的网,简称AOV网(Activity On Vertex network)。
如图所示,做出AOE网:
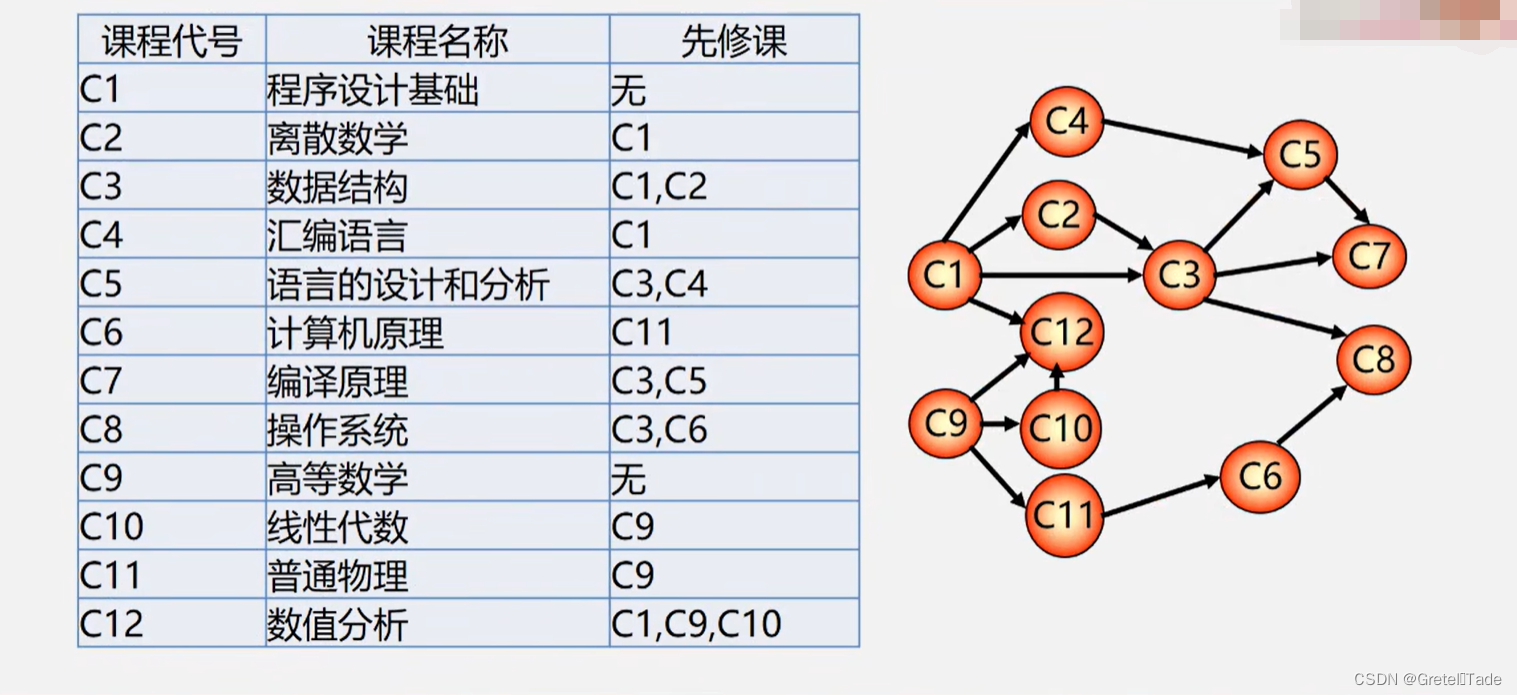
2.AOE网特征
- 若从i到j有一条有向路径,则i是j的前驱i是i的后继。
- 若<ij> 是网中有向边,则i是j的直接前驱;j是i的直接后继
- AOV 网中不允许有回路,因为如果有回路存在,则表明某项活动以自己为先决条件,显然这是荒谬的。
拓扑排序
1.基本概念
在AOV 网没有回路的前提下,我们将全部活动排列成一个线性序列,使得若AOV 网中有弧 <i,j>存在,则在这个序列中,i一定排在的前面,具有这种性质的线性序列称为拓扑有序序列,相应的拓扑有序排序的算法称为拓扑排序
拓扑排序是对一个有向图构造拓扑序列,解决工程是否能顺利进行的问题。构造时有 2 种结果:
- 此图全部顶点被输出:说明说明图中无「环」存在, 是 AOV 网
没有输出全部顶点:说明图中有「环」存在,不是 AOV 网
形象化理解:
排序类似 流程图一样 任务
例如早上起床的任务:
例如:这里你只有穿了衬衣才能穿外套,而不是穿了外套再穿衬衣

2.方法步骤
- 在有向图中选一个没有前驱的顶点且输出之
- 从图中删除该顶点和所有以它为尾的弧
- 重复上述两步,直至全部顶点均已输出:或者当图中不存在无前驱的顶点为止
示例1:
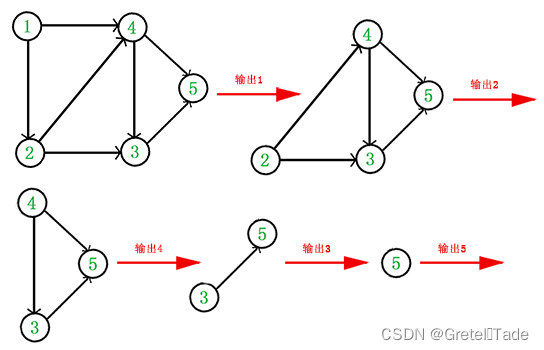
示例2:

3.拓扑排序的应用
检测AOV网中是否存在环方法:
对有向图构造其顶点的拓扑有序序列,若网中所有顶点都在它的拓扑有序序列中,则该AOV 网必定不存在环。
拓扑排序代码实现
图的存储方式有两种,邻接矩阵和邻接表,下面我就分别给出了这两种储存方式的代码写法。
1.邻接矩阵的代码
邻接矩阵结构如下:
#define Maxint 32767
#define Maxnum 100//最大顶点数//数据类型
typedef struct datatype {char id[10];//……
}
ElemType;
//图的邻接数组
typedef struct graph {ElemType vexs[Maxnum];//图数据int matrix[Maxnum][Maxnum];//二维数组矩阵int vexnum;//点数int arcnum;//边数
}Graph;拓扑排序代码:
//拓扑排序
void Topo_sort(Graph G) {int n = G.vexnum;int* result = (int*)malloc(sizeof(int) * n);//储存结果int* indegree = (int*)malloc(sizeof(int) * n);//入度int*queue= (int*)malloc(sizeof(int) * n);//队列,储存下标//初始化for (int i = 0; i < n; i++) {result[i] = -1;indegree[i] = 0;queue[i] = -1;}int que_count = 0;int count = 0;//统计每一个顶点的入度for (int x = 0; x < n; x++) {for (int y = 0; y < n; y++) {if (G.matrix[y][x] != 0 && G.matrix[y][x] != Maxint)indegree[x]++;}}//把入度为0的顶点放入队列for (int i = 0; i < n; i++) {if (indegree[i] == 0) {queue[que_count] = i;que_count++;}}//后继处理while (que_count > 0) {//出队操作int pop = queue[0];for (int j = 0; j < que_count-1; j++) {queue[j] = queue[j + 1];}que_count--;result[count++] = pop;for (int i = 0; i < n; i++) {if (G.matrix[pop][i] != 0 && G.matrix[pop][i] != Maxint) {indegree[i]--;//把与这个出队的顶点相连的后继顶点入度都-1//以上操作完成了之后,如果还有入度为0的顶点就进入到队列当中if (indegree[i] == 0) queue[que_count++] = i;}}}printf("拓扑排序结果:\n");for (int k = 0; k < n; k++) {printf("%s->", G.vexs[result[k]].id);}printf("end\nprint over!\n");//释放空间free(result);free(indegree);free(queue);result = queue = indegree = NULL;
}2.邻接表代码
队列头文件.h代码:
#pragma once
#include<stdio.h>
#include<string.h>
#include <stdbool.h>
#include<assert.h>//数据结构体
typedef struct datatype {char id[10];//字符串编号//………………
}ElemType;//定义节点
typedef struct node {ElemType data;struct node* next;
}Node;
//定义队列
typedef struct queue {int count; //计数Node* front;//指向队头指针Node* rear;//指向队尾指针
}Queue;void Queue_init(Queue* queue);//初始化
bool isEmpty(Queue* queue);//判空
void enQueue(Queue* queue, ElemType data);//入队
Node* deQueue(Queue* queue);//出队
ElemType head_data(Queue queue);//获取队头数据
队列源文件代码.c
#include"queue.h"//初始化
void Queue_init(Queue* queue) {assert(queue);queue->front = NULL;queue->rear = NULL;queue->count=0;
}//创建节点
Node* create_node(ElemType data) {Node* new_node = (Node*)malloc(sizeof(Node));if (new_node) {new_node->data = data;new_node->next = NULL;return new_node;}else{printf("ERRPR\n");}
}//判断是否空队列
bool isEmpty(Queue* queue) {assert(queue);if (queue->count == 0){return true;}return false;
}//入队
void enQueue(Queue* queue, ElemType data) {assert(queue);Node* new_node = create_node(data);if (queue->rear == NULL && queue->front == NULL ) {queue->front = new_node;queue->rear = new_node;queue->count++;}else{queue->rear->next = new_node;queue->rear = new_node;queue->count++;}}//出队
Node* deQueue(Queue* queue) {assert(queue);if (!isEmpty(queue)) {Node* deNode;if (queue->count == 1) {deNode = queue->front;queue->front = NULL;queue->rear = NULL;}else {deNode = queue->front;queue->front = deNode->next;}queue->count--;return deNode;}printf("error\n");return NULL;
}//获取队头数据
ElemType head_data(Queue queue) {return queue.front->data;
}
拓扑排序代码:
//数据结构体
typedef struct datatype {char id[10];//字符串编号//………………
}ElemType;
//边节点存储结构
typedef struct arcnode {int index;//指向顶点的位置int weight;//权struct arcnode* nextarc;//指向下一个边节点
}Anode;
//顶点结点存储结构
typedef struct vexnode {ElemType data;Anode* firstarc;
}Vhead;
//图结构
typedef struct {Vhead* vertices;int vexnum;int arcnum;
}Graph;//拓扑排序(邻接表)
void Topo_sort(Graph G) {int* inarry = (int*)malloc(sizeof(int) * G.vexnum);//统计每一个顶点的入度int* result= (int*)malloc(sizeof(int) * G.vexnum);//储存遍历结果//初始化for (int j = 0; j < G.vexnum; j++) {inarry[j] = 0;result[j] = -1;}Queue que;Queue_init(&que);//统计每个顶点的入度情况for (int i = 0; i < G.vexnum; i++) {Anode* p = G.vertices[i].firstarc;while (p) {inarry[p->index]++;p = p->nextarc;}}//把入度为0的节点放入队列for (int i = 0; i < G.vexnum; i++) {if (inarry[i] == 0)enQueue(&que, G.vertices[i].data);}int count = 0;while (!isEmpty(&que)) {//出队操作Node* pop = deQueue(&que);int pop_index = Locate_vex(G, pop->data.id);result[count++] = pop_index;//存入结果当中free(pop);pop = NULL;Anode* cur = G.vertices[pop_index].firstarc;while (cur) {//把与出队的顶点关联的点入度-1inarry[cur->index]--;//如果减掉入度之后入度为0的话就入队if (inarry[cur->index] == 0)enQueue(&que, G.vertices[cur->index].data);cur = cur->nextarc;}}printf("拓扑排序结果:\n");for (int i = 0; i < count; i++) {printf("%s->", G.vertices[result[i]].data.id);}printf("end\nprintf over!\n");//释放空间;free(inarry);free(result);inarry = result = NULL;
}以上就是本期的全部内容了,我们下次见!
分享一张壁纸: 
相关文章:

图的应用3.0-----拓扑排序
目录 前言 AOE网 1.相关概念 2.AOE网特征 拓扑排序 1.基本概念 2.方法步骤 3.拓扑排序的应用 拓扑排序代码实现 1.邻接矩阵的代码 2.邻接表代码 前言 今天我们学习图的应用----拓扑排序,说到排序,你们是不是会想到冒泡排序,插入排序…...

Unity之ShaderGraph如何实现冰冻效果
前言 今天我们来实现一个冰冻的效果,非常的炫酷哦。 如下图所示: 主要节点 Voronoi:根据输入UV生成 Voronoi 或Worley噪声。Voronoi 噪声是通过计算像素和点阵之间的距离生成的。通过由输入角度偏移控制的伪随机数偏移这些点,可以生成细胞簇。这些单元的规模以及产生的…...
解决 viteprees 中 vp-doc 内置样式影响组件预
解决 viteprees 中 vp-doc 样式影响组件预览 问题 当使用"vitepress": "1.0.0-rc.22"作为组件库文档时,会自动引入vitepress的默认主题, 其中vp-doc中有大量的html标签样式 ... .vp-doc table {display: block;border-collapse: …...

flask 和fastdeploy 快速部署 yolov3
服务端 from flask import Flask,request,render_template from flask import session,redirect,jsonify import cv2 import numpy as np import base64 import os import fastdeploy as fd import datetime,timeapp=Flask(__name__)from logging import config,getLogger lo…...
Go 反射
文章目录 获取类型和值获取属性的类型和值通过反射修改值获取方法的名称和类型调用方法反射的缺点 获取类型和值 之前讲过接口nil不一定等于空接口,因为一个 interface 底层 由 type value 构成,只有 type 和 value 都匹配,才能 reflect.Vl…...

竞赛选题 深度学习卷积神经网络垃圾分类系统 - 深度学习 神经网络 图像识别 垃圾分类 算法 小程序
文章目录 0 简介1 背景意义2 数据集3 数据探索4 数据增广(数据集补充)5 垃圾图像分类5.1 迁移学习5.1.1 什么是迁移学习?5.1.2 为什么要迁移学习? 5.2 模型选择5.3 训练环境5.3.1 硬件配置5.3.2 软件配置 5.4 训练过程5.5 模型分类效果(PC端) 6 构建垃圾…...

ts-node模块
ts-node模块 是一个非官方的npm模块,可以直接运行JS代码。 安装: npm install -g ts-node使用: ts-node script.ts如果不安装ts-node,可以通过npx在线调用ts-node,运行ts脚本。 npx ts-node script.ts...
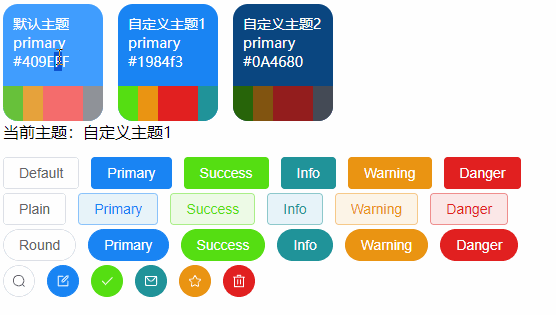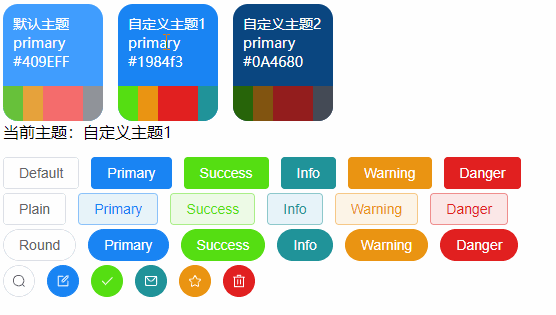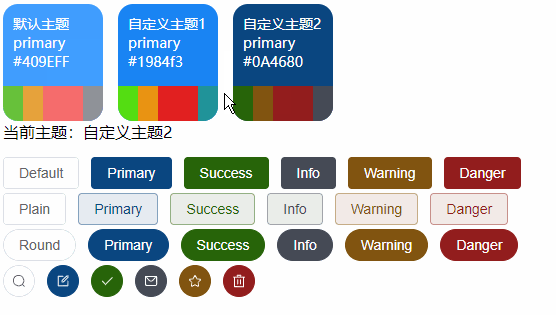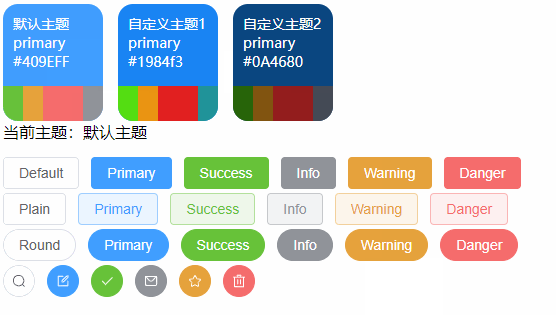
【VUE】ElementPlus之动态主题色调切换(Vue3 + Element Plus+Scss + Pinia)
前言 关于ElementPlus的基础主题色自定义可以参阅《【VUE】ElementPlus之自定义主题样式和命名空间》 有了上面基础的了解,我们知道ElementPlus的主题色调是基于CSS3变量特性进行全局控制的, 那么接下来我们也基于CSS3变量来实现主题色调的动态切换效果&…...
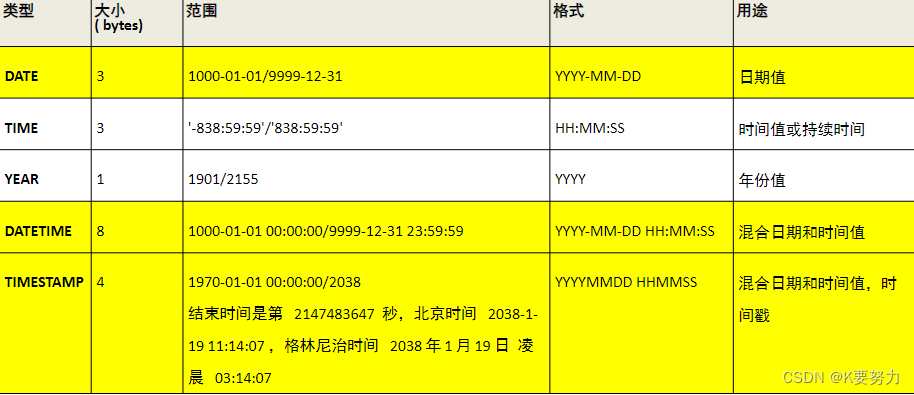
MySQL数据库基本操作1
文章目录 主要内容一.DDL1.创建表代码如下(示例): 2.创建表的类型3.其他操作4.修改表结构格式代码如下(示例): 二.DML1.数据插入代码如下(示例): 2.数据修改代码如下(示例): 3.数据删…...
Webpack简介及打包演示
Webpack 是一个静态模块打包工具,从入口构建依赖图,打包有关的模块,最后用于展示你的内容 静态模块:编写代码过程中的,html,css, js,图片等固定内容的文件 打包过程,注…...

面向对象设计模式——命令模式
命令设计模式(Command Pattern)是一种行为型设计模式,它的主要目的是将请求或操作封装成一个对象,从而允许参数化客户端对象,队列请求,将请求记录到日志,以及支持可撤销的操作。命令模式将请求的发出者(调用者)与请求的接收者(执行者)解耦,这使得系统更加灵活、可扩…...

selenium测试框架快速搭建(ui自动化测试)
一、介绍 selenium目前主流的web自动化测试框架;支持多种编程语言Java、pythan、go、js等;selenium 提供一系列的api 供我们使用,因此在web测试时我们要点页面中的某一个按钮,那么我们只需要获取页面,然后根据id或者n…...

TypeScript中的类型映射
类型映射 1. 简介 映射就是将一种类型按照映射规则,转成另一种类型,通常用于对象类型。 这里类型B通过A采用属性名索引的写法,完成了类型B的定义 type A {foo: number;bar: number; };type B {[prop in keyof A]: string; };这里复制了一…...

系统平台同一网络下不同设备及进程数据通讯--DDS数据分发服务中间件
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言(1)中间件的介绍(2)DDS介绍(3)发布者(4)订阅者(5)idl文件(定义msg结构体)(6)QoS(Quality of Service)策略(7)DDS测试工具介绍(…...

golang小技巧
1/有时需要把json内容返回给前段进行文本编辑json字段,那么最好是能返回格式化后的json,这样对于用户编辑页方便。这时候可以利用json.MarshalIndent(data, "", "\t")来进行格式化,带有缩进的marshal。 2/对holders的填…...

JavaWeb——IDEA操作:Project最终新建module
在project中创建新的module: 创建一个新的module很容易,但是它可能连接不上Tomcat,因此需要修改一些配置: 将以下地址修改为新module的地址...

前端开发技术栈(工具篇):2023深入了解webpack的安装和使用以及核心概念和启动流程(详细) 63.3k stars
目录 Webpack简介 Entry Module Chunk Loader Plugin Output Webpack的启动流程 Webpack的优缺点 Webpack的使用 1. 安装Webpack 2. 创建Webpack配置文件 3. 编写代码 4. 运行Webpack 5. 在HTML中引入打包后的文件 6. 执行编译命令 Webpack其他功能介绍 1. 使…...
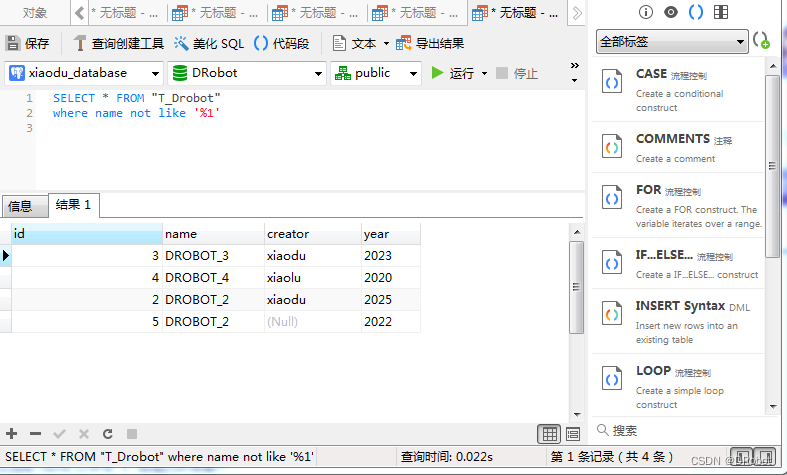
[SQL开发笔记]LIKE操作符:在 WHERE 子句中搜索列中的指定模式
一、功能描述: LIKE操作符:用于在 WHERE 子句中搜索列中的指定模式。 二、LIKE操作符语法详解: LIKE 语法 SELECT column1, column2,…FROM table_nameWHERE column LIKE pattern; 参数说明: (1)colum…...

flutter深研
https://www.douyin.com/video/7020336319058627853 关闭系统风扇 在 Windows 操作系统上安装和配置 Flutter 开发环境 - Flutter 中文文档 - Flutter 中文开发者网站 - Flutter...

TypeScript中的declare关键字
declare关键字 1. 简介 declare关键字用来告诉编译器,某个类型是存在的,可以在当前文件中使用。 作用:就是让当前文件可以使用其他文件声明的类型。比如,自己的脚本使用外部库定义的函数,编译器会因为不知道外部函数…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
