40.查找练习题(王道2023数据结构第7章)
试题1(王道7.2.4节综合练习5):
写出折半查找的递归算法。
#include<stdio.h>
#include<stdlib.h>
#include<string.h>#define MAXSIZE 10
#define ElemType int
#define Status inttypedef struct{int data[MAXSIZE]; //存储空间的基地址int length; //当前长度
}SqList;void CreatList(SqList &L){ //建立线性表L.length = 6;L.data[0] = 2;L.data[1] = 3;L.data[2] = 5;L.data[3] = 7;L.data[4] = 9;L.data[5] = 11;
}int BinarySearch(SqList L,ElemType x,int low,int high){int mid = (low + high) / 2;if(low > high)return -1;else if(L.data[mid] == x)return mid;else if(L.data[mid] < x)BinarySearch(L, x, mid + 1, high);elseBinarySearch(L, x, low, mid - 1);
}int main(){SqList L;CreatList(L);printf("%d", BinarySearch(L, 7, 0, 5));
}输出:
3试题2(王道7.2.4节综合练习6):
线性表中各结点检索概率不等时,可用如下策略提高顺序检索的效率:若找到指定的结点,则将该结点与前驱结点(若存在)交换,使得经常被检索的结点尽量位于表的前端。试设计在顺序结构和链式结构的线性表上实现上述策略的顺序检索算法。
此题可以联系链表练习题的第20题:
【试题再现】试题20:设头指针为L的带有表头结点的非循环双向链表,其每个结点中除有prior(前驱指针),data(数据),next(后继指针)域外,还有一个访问频度域freq。在链表被启用前,其值均初始化为零。每当在连表中进行一次Locate(L,x)运算时,令元素值为x的结点中freq域的值增1,并使此链表中结点保持按访问频度非递增的顺序排列,同时最近访问的结点排在频度相同的结点的前面,以便使频繁访问的结点总是靠近表头。试编写符合上述要求的Locate(L,x)运算的算法,该运算为函数过程,返回找到结点的地址,类型为指针型。
31.链表练习题(2)(王道2023数据结构2.3.7节16-25题)-CSDN博客![]() https://blog.csdn.net/qq_54708219/article/details/133151369顺序表实现:
https://blog.csdn.net/qq_54708219/article/details/133151369顺序表实现:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>#define MAXSIZE 10
#define ElemType int
#define Status inttypedef struct{int data[MAXSIZE]; //存储空间的基地址int length; //当前长度
}SqList;void CreatList(SqList &L){ //建立线性表L.length = 6;L.data[0] = 2;L.data[1] = 3;L.data[2] = 5;L.data[3] = 7;L.data[4] = 9;L.data[5] = 11;
}void PrintList(SqList L){for (int i = 0; i < L.length;i++){printf("%d ", L.data[i]);}
}int Search(SqList &L,ElemType x){int t;for (int i = 0; i < L.length;i++){if(L.data[i] == x){t = L.data[i - 1]; //交换L.data[i - 1] = x;L.data[i] = t;return i;} }return -1;
}int main(){SqList L;CreatList(L);PrintList(L);printf("\n");printf("%d\n", Search(L, 7));PrintList(L);
}输出:
2 3 5 7 9 11
3
2 3 7 5 9 11链表实现:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>#define MAXSIZE 10
#define ElemType int
#define Status int//单链表的数据结构
typedef struct LNode
{ElemType data;struct LNode *next;
}LNode, *LinkList;//初始化
int InitList(LinkList &L)
{L = (LNode *)malloc(sizeof(LNode));L->next = NULL;return 1;
}//输出
void PrintList(LinkList L)
{printf("当前单链表的所有元素:");LNode *p;p = L->next;while (p != NULL){printf("[%d] ", p->data);p = p->next;}printf("\n");
}int Create(LinkList &L)
{int n, e;LNode *temp = L;//声明一个指针指向头结点,用于遍历链表 printf("请输入要输入元素的个数:");scanf("%d", &n);for (int i = 1; i <= n; i++){LNode *a = (LNode*)malloc(sizeof(LNode));printf("请输入第%d元素的值:", (i));scanf("%d", &e);a->data = e;temp->next = a;a->next = NULL;temp = temp->next;}return 1;
}int Search(LinkList L,ElemType x){LinkList p = L;LinkList q = L;LinkList r;int i = 0;while(p!=NULL){if(p->data != x){p = p->next;i = i + 1;}else{if(i > 1){for (int j = 1; j <= i - 2; j++){q = q->next;} //q指向第i-2个元素r = q->next; //r指向第i-1个元素q->next = p;q = p->next; //q指向第i+1个元素p->next = r;r->next = q;}return i;}}return -1;
}int main(){LinkList L;InitList(L);Create(L);PrintList(L);printf("元素在链表第%d个位置\n", Search(L, 7));PrintList(L);
}
输出:
请输入要输入元素的个数:6
请输入第1元素的值:2
请输入第2元素的值:3
请输入第3元素的值:5
请输入第4元素的值:7
请输入第5元素的值:9
请输入第6元素的值:11
当前单链表的所有元素:[2] [3] [5] [7] [9] [11]
元素在链表第4个位置
当前单链表的所有元素:[2] [3] [7] [5] [9] [11]试题3(王道7.3.4节综合练习6):
设计算法,判断给定的二叉树是否是二叉排序树。
看其中序遍历序列是否是递增有序的即可:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>#define MAXSIZE 10
#define ElemType int//二叉排序树的结构体定义
typedef struct BiTNode{ElemType data; //数据域BiTNode *lchild; //指向左子树根节点的指针BiTNode *rchild; //指向右子树根节点的指针
}BiTNode, *BiTree;int BST_Insert(BiTree &T,ElemType k){ //构造一棵二叉排序树if(T==NULL){T = (BiTree)malloc(sizeof(BiTNode));T->data = k;T->lchild = NULL;T->rchild = NULL;return 1;}else if(k==T->data){return 0;}else if(k<T->data){return BST_Insert(T->lchild, k);}else{return BST_Insert(T->rchild, k);}
}int if_BST(BiTree T){int a[10];int i = 0;if (T!=NULL){if_BST(T->lchild);a[i] = T->data;i = i + 1;if_BST(T->rchild);}for (int j = 1; j <= i-1;j++){ //实际上a数组中元素是0到i-1if(a[j-1] >= a[j]){return 0;}}return 1;
}int main(){BiTree T=NULL;int a[5] = {4, 2, 1, 3, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}printf("%d",if_BST(T));return 0;
}
输出:
1试题4(王道7.3.4节综合练习7):
设计算法求指定结点在给定二叉排序树的层次。
老问题了,直接上递归:
int levelofNode(BiTree T, ElemType x,int level){if(T==NULL)return -1;else{if(T->data==x)return level;else{if(T->data<x)return levelofNode(T->rchild, x, level + 1);elsereturn levelofNode(T->lchild, x, level + 1);}}
}int main(){BiTree T=NULL;int a[5] = {4, 2, 1, 3, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}printf("%d",levelofNode(T,3,1));return 0;
}
输出:
3试题5(王道7.3.4节综合练习8):
利用二叉树的遍历思想编写一个判断二叉树是否是平衡二叉树的算法。
这里利用层次遍历每一个结点,检查平衡因子绝对值是否小于1。全部通过才返回True。
int Depth(BiTree T){if(T==NULL)return 0;else{return (Depth(T->lchild) >= Depth(T->rchild)) ? Depth(T->lchild) + 1 : Depth(T->rchild) + 1;}
}int abs(int x){return x >= 0 ? x : -x;
}bool ifBalanceTree(BiTree T){ //层次遍历每一个结点int balance = 0;Queue q;InitQueue(q);BiTree p = T;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);balance = abs(Depth(p->lchild) - Depth(p->rchild));if(balance > 1)return false;if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}return true;
}int main(){BiTree T=NULL;int a[5] = {1, 2, 3, 4, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}printf("%d",ifBalanceTree(T));return 0;
}输出:
1 //int a[5] = {4, 2, 1, 3, 5};
0 //int a[5] = {1, 2, 3, 4, 5};试题6(王道7.3.4节综合练习9):
设计算法求给定二叉排序树最小和最大的关键字。
最小关键字在最左下,最大关键字在最右下,抓住这一点判断即可。此题不需要从头遍历把所有结点全部输出。
int maxvalue(BiTree T){ //求最大关键字BiTree p=T;while (p->rchild!=NULL){p = p->rchild;}return p->data;
}int main(){BiTree T=NULL;int a[5] = {4, 2, 1, 3, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}printf("%d",maxvalue(T));return 0;
}int minvalue(BiTree T){ //求最小关键字BiTree p=T;while (p->lchild!=NULL){p = p->lchild;}return p->data;
}int main(){BiTree T=NULL;int a[5] = {4, 2, 1, 3, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}printf("%d",minvalue(T));return 0;
}试题7(王道7.3.4节综合练习10):
设计一个算法,从大到小输出二叉排序树中所有值不小于k的关键字。
倒序访问:显然先访问右子树,然后根结点,最后左子树,然后检查并输出。
void printoverk(BiTree T,int k){ //求最小关键字if(T!=NULL){printoverk(T->rchild, k);if(T->data>k){printf("%d ", T->data);}printoverk(T->lchild, k);}
}int main(){BiTree T=NULL;int a[5] = {4, 2, 1, 3, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}printoverk(T, 2);return 0;
}输出:
5 4 3试题8(王道7.3.4节综合练习11):
编写一个递归算法,在一棵具有n个结点的二叉排序树上查找第k小的元素,并返回该结点的指针。要求算法的平均时间复杂度是,二叉排序树每个结点中除了data,lchild,rchild外,增设一个count成员,保存以该结点为根的子树的结点个数。
函数的参数有两个:二叉树指针T和查找第k个最小元素。
//求树的结点数(递归)
int Number_Node(BiTree T){if(T==NULL)return 0;else{return Number_Node(T->lchild) + Number_Node(T->rchild) + 1;}
}int BST_Insert(BiTree &T,ElemType k){ //构造一棵二叉排序树if(T==NULL){T = (BiTree)malloc(sizeof(BiTNode));T->data = k;T->lchild = NULL;T->rchild = NULL;return 1;}else if(k==T->data){return 0;}else if(k<T->data){return BST_Insert(T->lchild, k);}else{return BST_Insert(T->rchild, k);}
}void BST_Insertcount(BiTree &T){ //修改count的数值Queue q;InitQueue(q);BiTree p = T;InsertQueue(q, p);while(!IsQueueEmpty(q)){p = DeleteQueue(q, p);p->count = Number_Node(p);if(p->lchild!=NULL)InsertQueue(q, p->lchild);if(p->rchild!=NULL)InsertQueue(q, p->rchild);}
}BiTree SearchSmallk(BiTree T,int k){ //寻找第k小的元素if(k<1||k>T->count) //k不合法,直接返回空return NULL;if(T->lchild == NULL){if(k == 1)return T;elsereturn SearchSmallk(T->rchild, k - 1); //第k小的元素必在右子树}else{if(T->lchild->count == k-1)return T;else if(T->lchild->count < k-1)return SearchSmallk(T->rchild, k - T->lchild->count - 1); //第k小的元素必在右子树elsereturn SearchSmallk(T->lchild, k); //第k小的元素必在左子树}
}int main(){BiTree T=NULL;BiTree p;int a[5] = {4, 2, 1, 3, 5}; //以王道第10题做验证for (int i = 0; i <= 4;i++){BST_Insert(T, a[i]);}BST_Insertcount(T);p = SearchSmallk(T, 3);printf("%d", p->data);return 0;
}输出:
3相关文章:
40.查找练习题(王道2023数据结构第7章)
试题1(王道7.2.4节综合练习5): 写出折半查找的递归算法。 #include<stdio.h> #include<stdlib.h> #include<string.h>#define MAXSIZE 10 #define ElemType int #define Status inttypedef struct{int data[MAXSIZE]; /…...

Segmentation fault 的bug解决
一,Segmentation fault 的bug解决 问题描述:自己在使用CPU上调试完代码之后,可以稳定运行,有输出结果。 但是把数据和模型加载上GPU之后,出现了报错。 Segmentation fault (core dumped) 搜了一下可能存在的原因&…...

【Python机器学习】零基础掌握BaggingRegressor集成学习
如何提升回归模型的稳定性和准确性? 在实际生活中,比如房价预测,经常会遇到一种情况:有大量的特征和样本数据,但模型的预测准确度仍然不尽人意。这时候,单一的模型(如支持向量机回归)可能表现得并不够好。 考虑到这个问题,解决方案可能是使用集成方法,特别是Baggin…...
麒麟KYLINOS通过命令行配置kysec的防火墙
原文链接:麒麟KYLINOS通过命令行配置kysec的防火墙 hello,大家好啊,今天给大家带来一篇使用命令行配置kysec的防火墙的文章,通过本篇文章的学习,大家可以了解到图形化界面中的防火墙信息是如何生成的,为后期…...

磁盘监控:告警时发送邮件
1.配置邮箱 1.编辑邮箱配置文件 vim /etc/mail.rc2.在末尾输入自己的邮箱配置,以163邮箱为例 #开启ssl set ssl-verifyignore #证书目录,下方为centos系统证书默认位置,也自行生成证书并指定 set nss-config-dir/etc/pki/nssdb # 配置的第…...
【HarmonyOS】元服务卡片router实现跳转到指定页面并传动态参数
【关键字】 元服务卡片、router跳转不同页面、传递动态参数 【写在前面】 本篇文章主要介绍开发元服务卡片时,如何实现从卡片中点击事件跳转到指定的应用内页面,并传递参数接受参数功能。此处以JS UI开发服务卡片为例,JS卡片支持组件设置ac…...
Centos安装RabbitMQ,JavaSpring发送RabbitMQ延迟延时消息,JavaSpring消费RabbitMQ消息
1,版本说明 erlang 和 rabbitmq 版本说明 https://www.rabbitmq.com/which-erlang.html 确认需要安装的mq版本以及对应的erlang版本。 2,下载安装文件 RabbitMQ下载地址: https://packagecloud.io/rabbitmq/rabbitmq-server Erlang下载地…...
leetcode:1323. 6 和 9 组成的最大数字(python3解法)
难度:简单 给你一个仅由数字 6 和 9 组成的正整数 num。 你最多只能翻转一位数字,将 6 变成 9,或者把 9 变成 6 。 请返回你可以得到的最大数字。 示例 1: 输入:num 9669 输出:9969 解释: 改变…...
SpringBoot集成Redis Cluster集群(附带Linux部署Redis Cluster高可用集群)
目录 一、前言二、集成配置2.1、POM2.2、添加配置文件application.yml2.3、编写配置文件2.4、编写启动类2.5、编写测试类测试是否连接成功 一、前言 这里会使用到spring-boot-starter-data-redis包,spring boot 2的spring-boot-starter-data-redis中,默…...
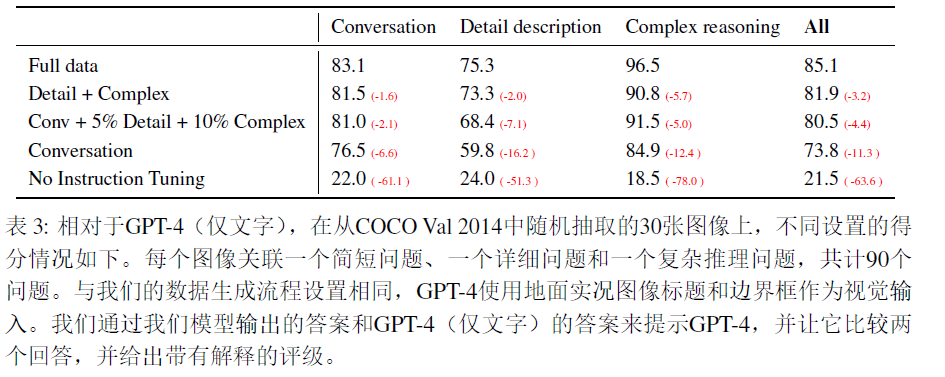
LLaVA:visual instruction tuning
对近期一些MLLM(Multimodal Large Language Model)的总结 - 知乎本文将从模型结构,训练方法,训练数据,模型表现四个方面对近期的一些MLLM(Multi-modal Large Language Models)进行总结并探讨这四个方面对模型表现的影响…...

Python实现双目标定、畸变矫正、立体矫正
一,双目标定、畸变矫正、立体矫正的作用 双目目标定: 3D重建和测距:通过双目目标定,您可以确定两个摄像头之间的相对位置和朝向,从而能够根据视差信息计算物体的深度,进行三维重建和测距。姿态估计…...
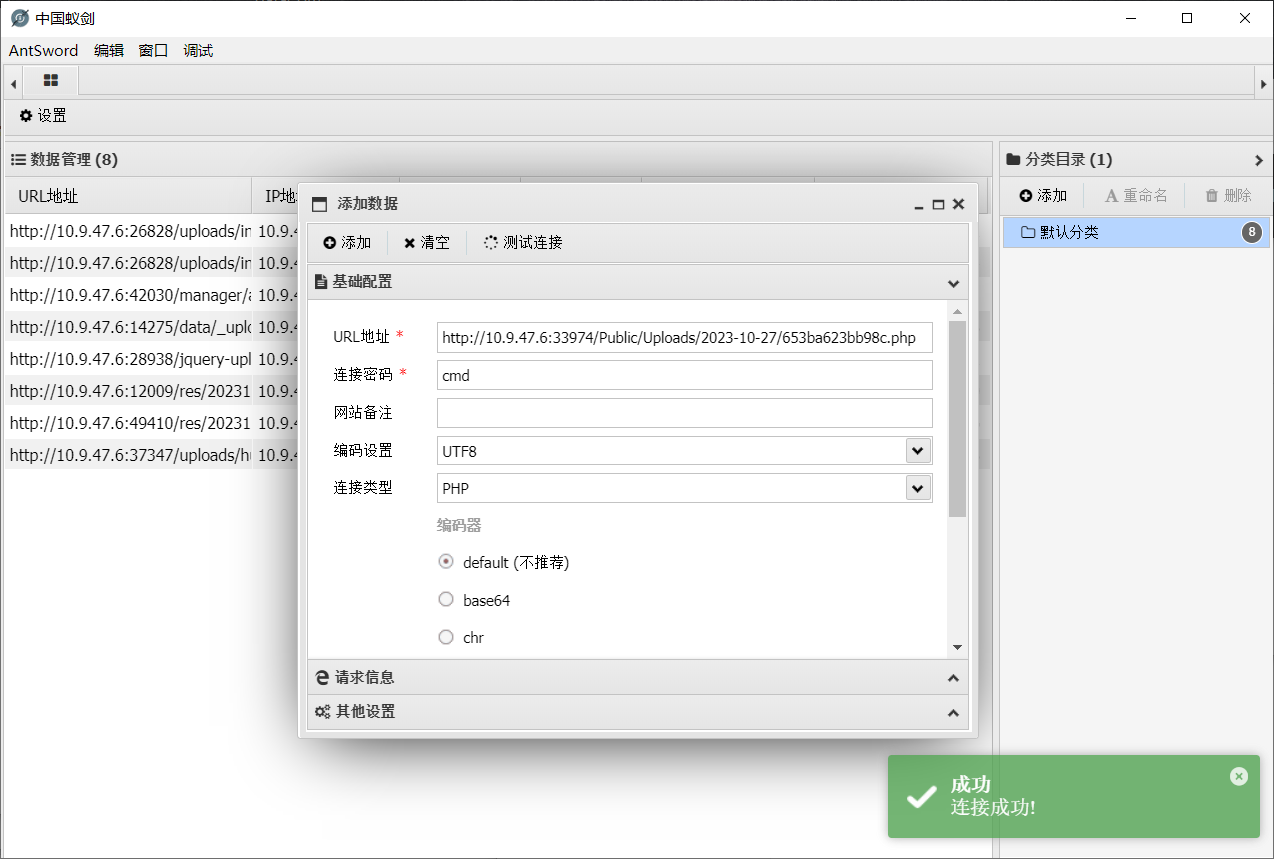
showdoc 文件上传 (cnvd-2020-26585)
showdoc 文件上传 (cnvd-2020-26585) 描述 ShowDoc是一个非常适合IT团队的在线API文档、技术文档工具。通过showdoc,你可以方便地使用markdown语法来书写出美观的API文档、数据字典文档、技术文档、在线excel文档等等。 api_page存在任意文…...

Java数据类型,变量与运算符
1.字面常量 常量是在程序运行期间,固定不变的量称为常量。 public class HelloWorld{public static void main(String[] args){System.out.println("Hello,world");} } 在以上程序中,输出的Hello Word,其中的“Hello Word”就是…...

Linux nm命令
Linux的nm命令主要用于列出对象文件中的符号。以下是一些使用示例: 基本用法:只需运行’nm’命令,并将对象文件的名称作为输入传递给它。例如,我使用’nm’命令与’apl’elf 文件:nm apl。 在输出中为每个符号前面添加…...

iOS发布证书.p12文件无密码解决办法及导出带密码的新.p12文件方法
摘要: 本文将以iOS技术博主身份,分享解决使用无密码的.p12文件发布应用时遇到的问题,并介绍如何以带密码的方式重新导出.p12文件的方法。通过本文提供的步骤,开发者可以顺利完成证书的发布流程。 引言 在iOS应用发布过程中&…...

OpenCamera拍照的代码流程
按理来说,拍照应该是很简单的。随着功能的复杂,代码也是越来越多,流程越来越长。想看看地理位置是怎么保存的,于是就研究了一下OpenCamera的拍照流程。在回调时有点乱。 MainActivity clickedTakePhoto() takePicture() takePic…...
华为OD机考算法题:矩阵最大值
题目部分 题目矩阵最大值难度难题目说明给定一个仅包含 0 和 1 的 N*N 二维矩阵,请计算二维矩阵的最大值,计算规则如下: 1. 每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行…...
【Javascript】函数之形参与实参
function c(a,b){return ab;}var sumc(3,4);console.log(sum);a,b为形参 3,4为实参 形参和实参是⼀⼀对应的数量可以不对应参数的类型不确定函数可以设置默认参数实参可以是字⾯量也可以是变量...

PAT 乙级1090危险品装箱
题目: 集装箱运输货物时,我们必须特别小心,不能把不相容的货物装在一只箱子里。比如氧化剂绝对不能跟易燃液体同箱,否则很容易造成爆炸。 本题给定一张不相容物品的清单,需要你检查每一张集装箱货品清单,…...
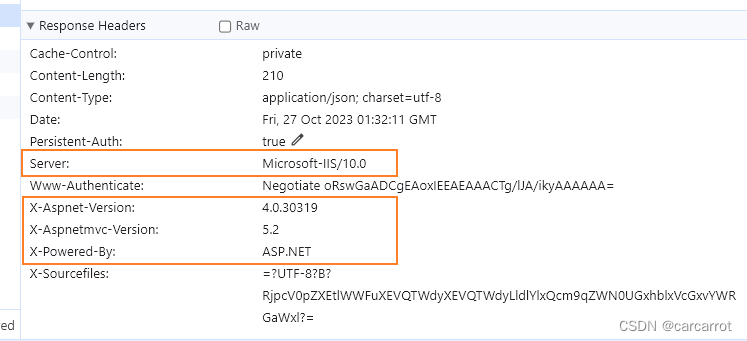
Response Header中不暴露Server(IIS)版本、ASP.NET及相关版本等信息
ASP MVC开发的Web默认情况下会在请求的回应中暴露Server、X-AspNet-Version、X-AspNetMvc-Version、X-Powered-By等相关服务端信息,公开这些敏感信息会存在一定的安全风险。 X-SourceFiles标头用于被IIS / IIS Express中某些调试模块理解,它包含到磁盘上…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
