LeetCode 1465. 切割后面积最大的蛋糕:纵横分别处理
【LetMeFly】1465.切割后面积最大的蛋糕:纵横分别处理
力扣题目链接:https://leetcode.cn/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts/
矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCuts 和 verticalCuts,其中:
-
horizontalCuts[i]是从矩形蛋糕顶部到第i个水平切口的距离 verticalCuts[j]是从矩形蛋糕的左侧到第j个竖直切口的距离
请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后,请你找出 面积最大 的那份蛋糕,并返回其 面积 。由于答案可能是一个很大的数字,因此需要将结果 对 109 + 7 取余 后返回。
示例 1:
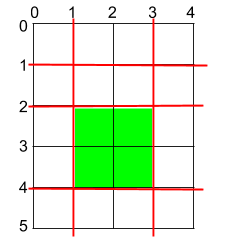
输入:h = 5, w = 4, horizontalCuts = [1,2,4], verticalCuts = [1,3] 输出:4 解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色的那份蛋糕面积最大。
示例 2:
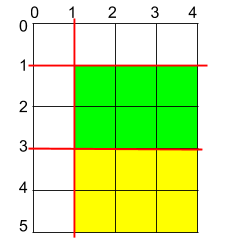
输入:h = 5, w = 4, horizontalCuts = [3,1], verticalCuts = [1] 输出:6 解释:上图所示的矩阵蛋糕中,红色线表示水平和竖直方向上的切口。切割蛋糕后,绿色和黄色的两份蛋糕面积最大。
示例 3:
输入:h = 5, w = 4, horizontalCuts = [3], verticalCuts = [3] 输出:9
提示:
2 <= h, w <= 1091 <= horizontalCuts.length <= min(h - 1, 105)1 <= verticalCuts.length <= min(w - 1, 105)1 <= horizontalCuts[i] < h1 <= verticalCuts[i] < w- 题目数据保证
horizontalCuts中的所有元素各不相同 - 题目数据保证
verticalCuts中的所有元素各不相同
方法一:纵横分别处理
横向的一刀和纵向的一刀之间是互不干扰的。因此,我们只需要求出“横向上的最大间隔”和“纵向上的最大间隔”,然后相乘即可。
对于单个方向:我们只需要求出“相邻两刀”的最大间隔,以及第一刀和最后一刀距离边界的值的最大值即可。
- 时间复杂度 O ( n log n + m log m ) O(n\log n + m\log m) O(nlogn+mlogm)
- 空间复杂度 O ( log n + log m ) O(\log n + \log m) O(logn+logm)
AC代码
C++
class Solution {
private:long long getMax(int l, vector<int>& v) {sort(v.begin(), v.end());int ans= 0;for (int i = 1; i < v.size(); i++) {ans = max(ans, v[i] - v[i - 1]);}return max(ans, max(v[0], l - v[v.size() - 1]));}public:int maxArea(int h, int w, vector<int>& horizontalCuts, vector<int>& verticalCuts) {return getMax(h, horizontalCuts) * getMax(w, verticalCuts) % 1000000007;}
};
Python
# from typing import Listclass Solution:def getMax(self, l: int, v: List[int]) -> int:v.sort()ans = v[0]for i in range(1, len(v)):ans = max(ans, v[i] - v[i - 1])return max(ans, l - v[-1])def maxArea(self, h: int, w: int, horizontalCuts: List[int], verticalCuts: List[int]) -> int:return self.getMax(h, horizontalCuts) * self.getMax(w, verticalCuts) % 1000000007
同步发文于CSDN,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/134073948
相关文章:

LeetCode 1465. 切割后面积最大的蛋糕:纵横分别处理
【LetMeFly】1465.切割后面积最大的蛋糕:纵横分别处理 力扣题目链接:https://leetcode.cn/problems/maximum-area-of-a-piece-of-cake-after-horizontal-and-vertical-cuts/ 矩形蛋糕的高度为 h 且宽度为 w,给你两个整数数组 horizontalCut…...

YTM32的增强型定时器eTMR外设模块详解
文章目录 eTMR外设简介eTMR工作机制系统框图引脚与信号计数器与时钟源输出比较模式PWM模式通道配对通道对的互补输出(Complementary Mode)双缓冲输出PWM(Double Switch)错误检测机制(Fault Detection) 输入…...
40.查找练习题(王道2023数据结构第7章)
试题1(王道7.2.4节综合练习5): 写出折半查找的递归算法。 #include<stdio.h> #include<stdlib.h> #include<string.h>#define MAXSIZE 10 #define ElemType int #define Status inttypedef struct{int data[MAXSIZE]; /…...

Segmentation fault 的bug解决
一,Segmentation fault 的bug解决 问题描述:自己在使用CPU上调试完代码之后,可以稳定运行,有输出结果。 但是把数据和模型加载上GPU之后,出现了报错。 Segmentation fault (core dumped) 搜了一下可能存在的原因&…...

【Python机器学习】零基础掌握BaggingRegressor集成学习
如何提升回归模型的稳定性和准确性? 在实际生活中,比如房价预测,经常会遇到一种情况:有大量的特征和样本数据,但模型的预测准确度仍然不尽人意。这时候,单一的模型(如支持向量机回归)可能表现得并不够好。 考虑到这个问题,解决方案可能是使用集成方法,特别是Baggin…...
麒麟KYLINOS通过命令行配置kysec的防火墙
原文链接:麒麟KYLINOS通过命令行配置kysec的防火墙 hello,大家好啊,今天给大家带来一篇使用命令行配置kysec的防火墙的文章,通过本篇文章的学习,大家可以了解到图形化界面中的防火墙信息是如何生成的,为后期…...

磁盘监控:告警时发送邮件
1.配置邮箱 1.编辑邮箱配置文件 vim /etc/mail.rc2.在末尾输入自己的邮箱配置,以163邮箱为例 #开启ssl set ssl-verifyignore #证书目录,下方为centos系统证书默认位置,也自行生成证书并指定 set nss-config-dir/etc/pki/nssdb # 配置的第…...
【HarmonyOS】元服务卡片router实现跳转到指定页面并传动态参数
【关键字】 元服务卡片、router跳转不同页面、传递动态参数 【写在前面】 本篇文章主要介绍开发元服务卡片时,如何实现从卡片中点击事件跳转到指定的应用内页面,并传递参数接受参数功能。此处以JS UI开发服务卡片为例,JS卡片支持组件设置ac…...
Centos安装RabbitMQ,JavaSpring发送RabbitMQ延迟延时消息,JavaSpring消费RabbitMQ消息
1,版本说明 erlang 和 rabbitmq 版本说明 https://www.rabbitmq.com/which-erlang.html 确认需要安装的mq版本以及对应的erlang版本。 2,下载安装文件 RabbitMQ下载地址: https://packagecloud.io/rabbitmq/rabbitmq-server Erlang下载地…...
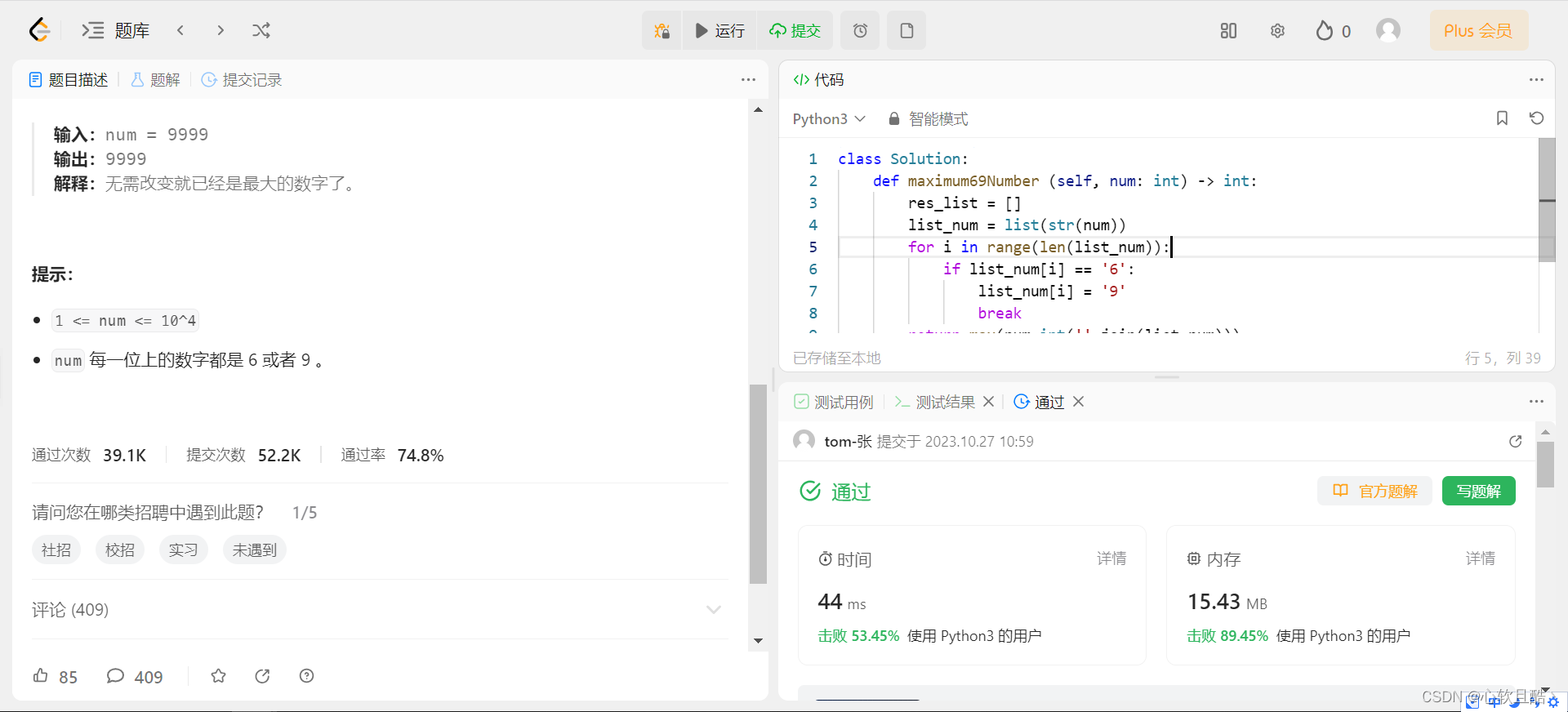
leetcode:1323. 6 和 9 组成的最大数字(python3解法)
难度:简单 给你一个仅由数字 6 和 9 组成的正整数 num。 你最多只能翻转一位数字,将 6 变成 9,或者把 9 变成 6 。 请返回你可以得到的最大数字。 示例 1: 输入:num 9669 输出:9969 解释: 改变…...
SpringBoot集成Redis Cluster集群(附带Linux部署Redis Cluster高可用集群)
目录 一、前言二、集成配置2.1、POM2.2、添加配置文件application.yml2.3、编写配置文件2.4、编写启动类2.5、编写测试类测试是否连接成功 一、前言 这里会使用到spring-boot-starter-data-redis包,spring boot 2的spring-boot-starter-data-redis中,默…...
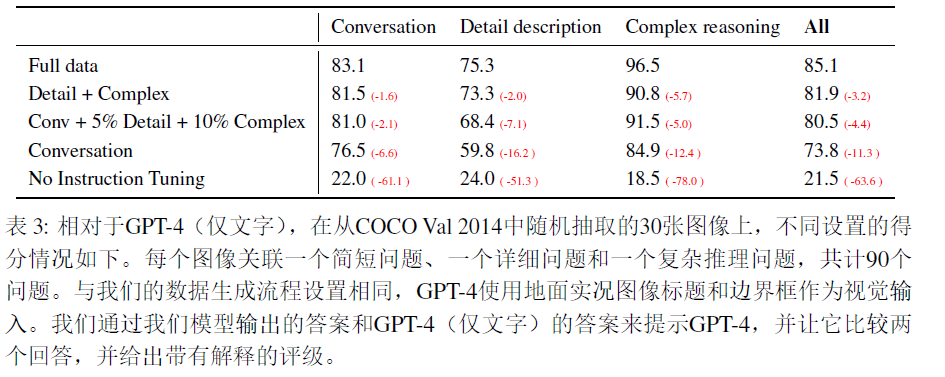
LLaVA:visual instruction tuning
对近期一些MLLM(Multimodal Large Language Model)的总结 - 知乎本文将从模型结构,训练方法,训练数据,模型表现四个方面对近期的一些MLLM(Multi-modal Large Language Models)进行总结并探讨这四个方面对模型表现的影响…...

Python实现双目标定、畸变矫正、立体矫正
一,双目标定、畸变矫正、立体矫正的作用 双目目标定: 3D重建和测距:通过双目目标定,您可以确定两个摄像头之间的相对位置和朝向,从而能够根据视差信息计算物体的深度,进行三维重建和测距。姿态估计…...
showdoc 文件上传 (cnvd-2020-26585)
showdoc 文件上传 (cnvd-2020-26585) 描述 ShowDoc是一个非常适合IT团队的在线API文档、技术文档工具。通过showdoc,你可以方便地使用markdown语法来书写出美观的API文档、数据字典文档、技术文档、在线excel文档等等。 api_page存在任意文…...

Java数据类型,变量与运算符
1.字面常量 常量是在程序运行期间,固定不变的量称为常量。 public class HelloWorld{public static void main(String[] args){System.out.println("Hello,world");} } 在以上程序中,输出的Hello Word,其中的“Hello Word”就是…...

Linux nm命令
Linux的nm命令主要用于列出对象文件中的符号。以下是一些使用示例: 基本用法:只需运行’nm’命令,并将对象文件的名称作为输入传递给它。例如,我使用’nm’命令与’apl’elf 文件:nm apl。 在输出中为每个符号前面添加…...

iOS发布证书.p12文件无密码解决办法及导出带密码的新.p12文件方法
摘要: 本文将以iOS技术博主身份,分享解决使用无密码的.p12文件发布应用时遇到的问题,并介绍如何以带密码的方式重新导出.p12文件的方法。通过本文提供的步骤,开发者可以顺利完成证书的发布流程。 引言 在iOS应用发布过程中&…...

OpenCamera拍照的代码流程
按理来说,拍照应该是很简单的。随着功能的复杂,代码也是越来越多,流程越来越长。想看看地理位置是怎么保存的,于是就研究了一下OpenCamera的拍照流程。在回调时有点乱。 MainActivity clickedTakePhoto() takePicture() takePic…...
华为OD机考算法题:矩阵最大值
题目部分 题目矩阵最大值难度难题目说明给定一个仅包含 0 和 1 的 N*N 二维矩阵,请计算二维矩阵的最大值,计算规则如下: 1. 每行元素按下标顺序组成一个二进制数(下标越大越排在低位),二进制数的值就是该行…...
【Javascript】函数之形参与实参
function c(a,b){return ab;}var sumc(3,4);console.log(sum);a,b为形参 3,4为实参 形参和实参是⼀⼀对应的数量可以不对应参数的类型不确定函数可以设置默认参数实参可以是字⾯量也可以是变量...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
