八皇后问题
1、问题描述
在棋盘上放置 8 个皇后,使得它们互不攻击,此时每个皇后的攻击范围为同行同列和同对角线,要求找出所有解,如下图所示。
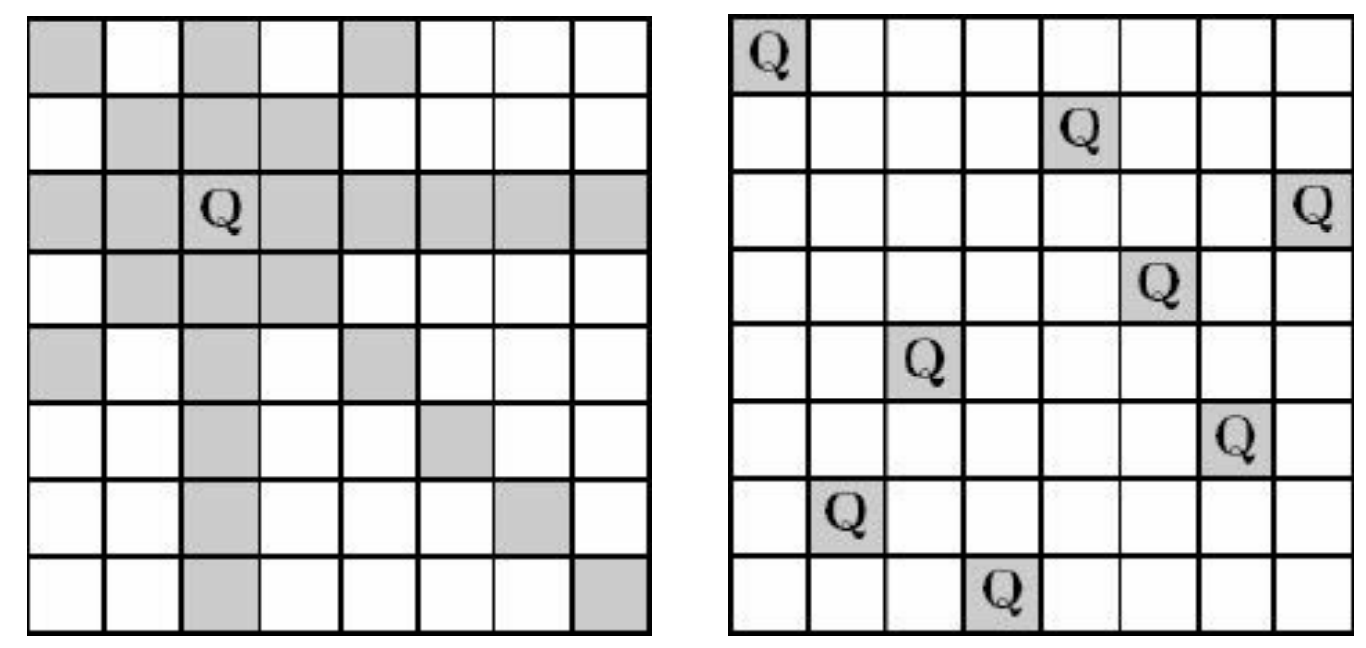
左图为皇后的攻击范围,右图为一个可行解。
2、分析
最简单的思路是把问题转化为 “从 64 个格子中选一个子集”,使得 “子集中恰好 8 个格子,且任意两个选出的格子都不在同一行、同一列或同一个对角线上”。这正是子集枚举问题。然而,64个格子的子集有264 个,太大了,这并不是一个很好的模型。
第二个思路是把问题转化为 “从 64 个格子中选 8 个格子”,这是组合生成问题。根据组合数学,有 C 64 8 = 4.426 × 1 0 9 C_{64}^8 = 4.426 \times 10^9 C648=4.426×109 种方案,比第一种方案优秀,但仍然不够好。
经过思考,不难发现以下事实:恰好每行每列各放置一个皇后。如果用 C[x] 表示第 x 行皇后的列编号,则问题变成了全排列生成问题。 而 0 ~ 7 的排列一共只有 8! = 40320个,枚举量不会超过它。
提示:在编写递归枚举程序之前,需要深入分析问题,对模型精雕细琢。一般还应对解答树的结点数有一个粗略的估计,作为评价模型的重要依据,如下图所示。
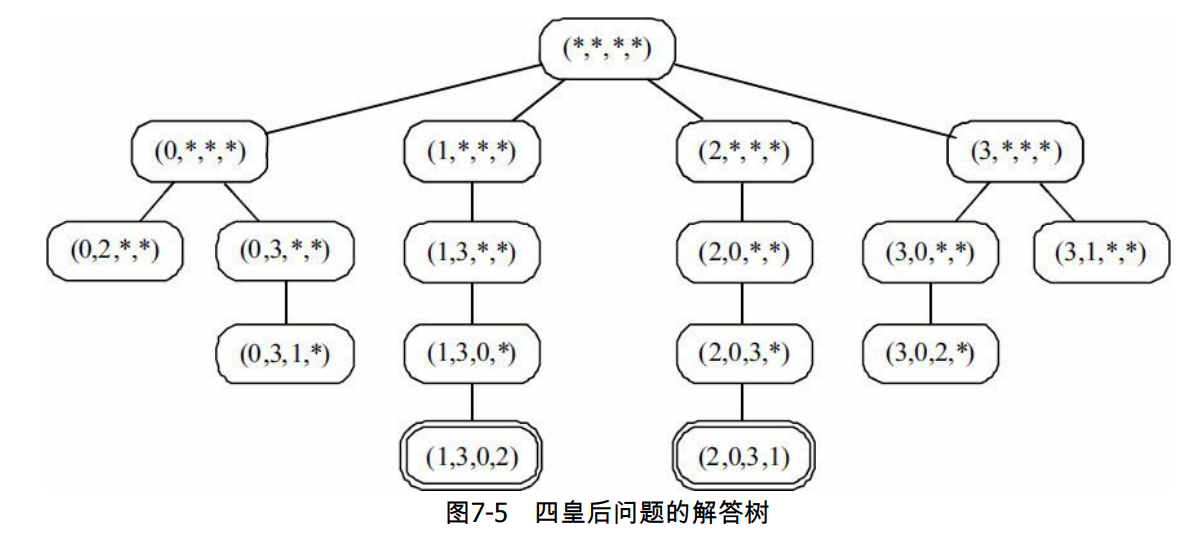
图中给出四皇后问题的完整解答树。它只有 17 个结点,比 4! = 24 小。之所以会这样,是因为有些结点无法继续扩展。如在 (0,2,*,*) 中,第2行无论将皇后放到哪里,都会和第 0 行和第1行中已放好的皇后发生冲突,其他还未放置的皇后更是如此。
在这种情况下,递归函数将不再递归调用它自身,而是返回上一层调用,这种现象称为回溯(backtracking)。
提示:当把问题分成若干步骤并递归求解时,如果当前步骤没有合法的选择,则函数将返回上一级递归调用,这种现象称为回溯。正是因为这个原因,递归枚举算法常被称为回溯法,应用十分普遍。
下面的程序简洁地求解了八皇后问题。在主程序中读入 n n n,并为 t o t tot tot 清零,然后调用 search(0),即可得到解的个数 tot。
void search(int cur) {if (cur == n) //递归边界,只要走到了这里,所有皇后必然不冲突tot++; else {for (int i = 0; i < n; i++) {int ok = 1;C[cur] = i; //尝试把第cur行的皇后放到第i列for (int j = 0; j < cur; j++) { //检查是否和前面的皇后冲突if (C[cur] == C[j] || cur - C[cur] == j - C[j] || cur + C[cur] == j + C[j]) {ok = 0;break;}}if (ok) search(cur + 1); //如果合法,继续递归}}
}
注意:既然是逐行放置的,则皇后肯定不会横向攻击,因此只需检查是否纵向和斜向攻击即可。条件 “cur - C[cur] == j - C[j] || cur + C[cur] == j + C[j]” 用来判断皇后 (cur, C[cur]) 和 (j, C[j]) 是否在同一条对角线上。其原理可用下图来说明。
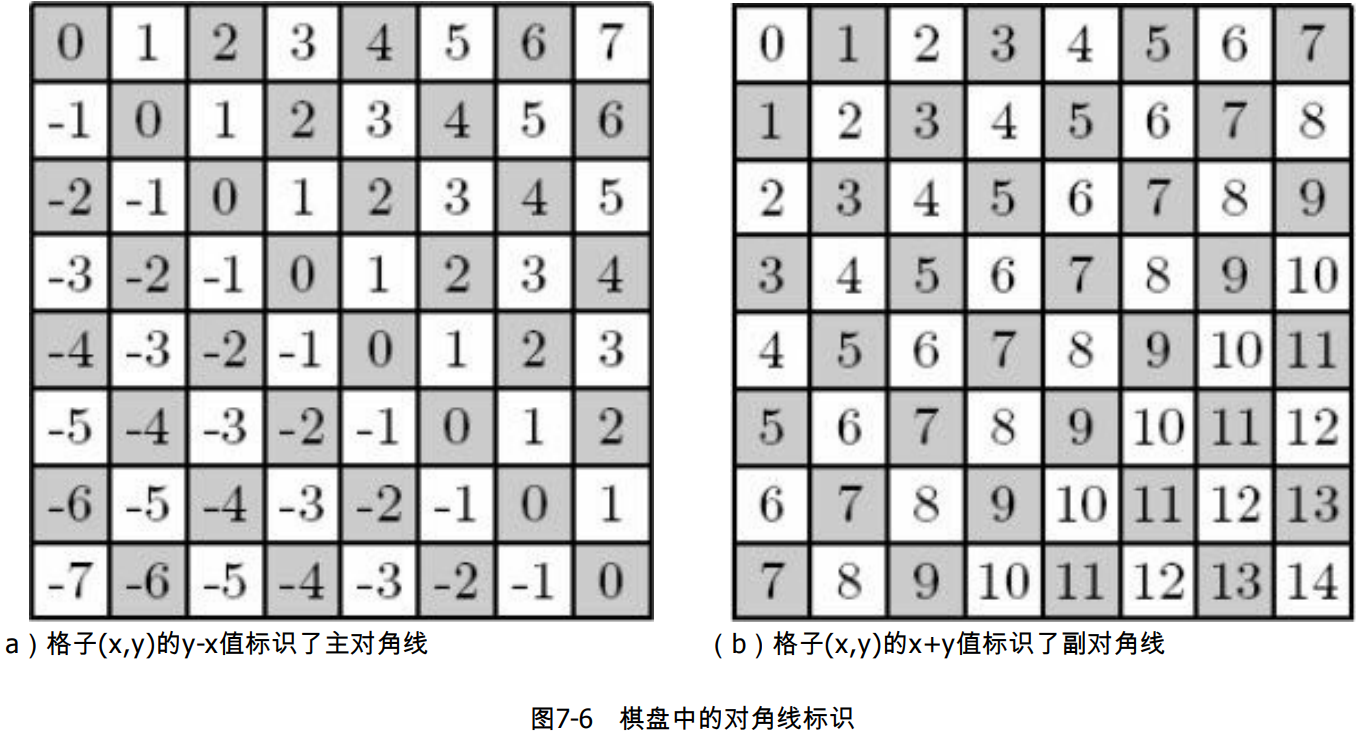
结点数似乎很难进一步减少了,但程序效率可以继续提高:利用二维数组 vis[2][] 直接判断当前尝试的皇后所在的列和两个对角线是否已有其他皇后。注意到主对角线标识 y − x y-x y−x 可能为负,存取时要加上 n n n。
void search(int cur) {if(cur == n) tot++;else {for(int i = 0; i < n; i++) {if(!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n]) { //利用二维数组直接判断C[cur] = i; //如果不用打印解,整个C数组都可以省略vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1; //修改全局变量search(cur+1);vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0; //切记!一定要改回来}}}
}
上面程序有个极其关键的地方:vis 数组的使用。vis数组的确切含义:表示已经放置的皇后占据了哪些列、主对角线和副对角线。将来放置的皇后不应该修改这些值——至少“看上去没有修改”。一般地,如果在回溯法中修改了辅助的全局变量,则一定要及时把它们恢复原状(除非故意保留所做修改)。 另外,在调用之前一定要把 vis 数组清空。
提示:如果在回溯法中使用了辅助的全局变量,则一定要及时把它们恢复原状。特别地,若函数有多个出口,则需在每个出口处恢复被修改的值。
3、完整代码
n皇后问题:生成-测试法
#include<cstdio>
using namespace std;int C[50], tot = 0, n = 8, nc = 0;void search(int cur) {int i, j;nc++;if(cur == n) {for(i = 0; i < n; i++)for(j = i+1; j < n; j++)if(C[i] == C[j] || i-C[i] == j-C[j] || i+C[i] == j+C[j]) return;tot++;} else {for(i = 0; i < n; i++) {C[cur] = i;search(cur+1);}}
}int main() {scanf("%d", &n);search(0);printf("%d\n", tot);printf("%d\n", nc);return 0;
}
n皇后问题:普通回溯法
#include<cstdio>
using namespace std;int C[50], tot = 0, n = 8, nc = 0;void search(int cur) {int i, j;nc++;if(cur == n) {tot++;} else { for(i = 0; i < n; i++) {int ok = 1;C[cur] = i;for(j = 0; j < cur; j++) {if(C[cur] == C[j] || cur-C[cur] == j-C[j] || cur+C[cur] == j+C[j]) {ok = 0;break;}}if(ok) search(cur+1);}}
}int main() {scanf("%d", &n);search(0);printf("%d\n", tot);printf("%d\n", nc);return 0;
}
n皇后问题:优化的回溯法
#include<cstdio>
#include<cstring>
using namespace std;int C[50], vis[3][50], tot = 0, n = 8, nc = 0;void search(int cur) {int i, j;nc++;if(cur == n) {tot++;} else for(i = 0; i < n; i++) {if(!vis[0][i] && !vis[1][cur+i] && !vis[2][cur-i+n]) {C[cur] = i;vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1;search(cur+1);vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0;}}
}int main() {scanf("%d", &n);memset(vis, 0, sizeof(vis));search(0);printf("%d\n", tot);printf("%d\n", nc);return 0;
}
相关文章:

八皇后问题
1、问题描述 在棋盘上放置 8 个皇后,使得它们互不攻击,此时每个皇后的攻击范围为同行同列和同对角线,要求找出所有解,如下图所示。 左图为皇后的攻击范围,右图为一个可行解。 2、分析 最简单的思路是把问题转化为 “…...
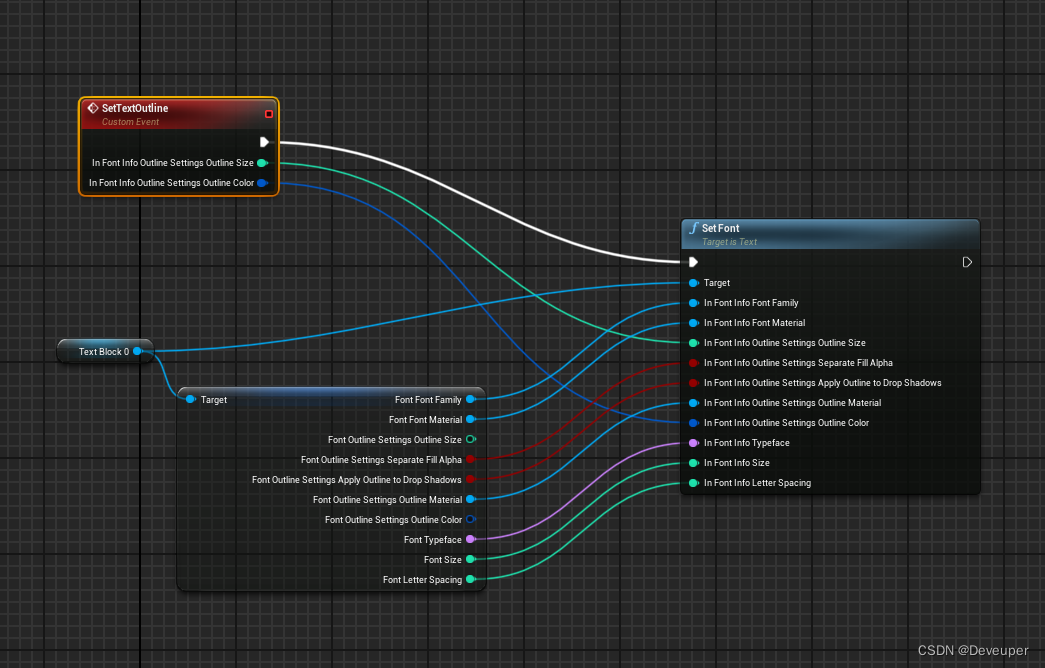
UE4/UE5 设置widget中text的字体Outline
想要在蓝图中控制Widget 中的 text字体,对字体outline参数进行设置。 但是蓝图中无法直接获取设置outline参数的方法: 没有outline相关的蓝图函数 该参数本身是在Font类别下的扩展,所以只要获取设置Font参数即可进行outline的设置 text连出…...
漏洞复现-phpmyadmin_SQL注入 (CVE-2020-5504)
phpmyadmin SQL注入 _(CVE-2020-5504) 漏洞信息 CVE-2020-5504sql注入漏洞Phpmyadmin 5.00以下 描述 phpMyAdmin是Phpmyadmin团队的一套免费的、基于Web的MySQL数据库管理工具。该工具能够创建和删除数据库,创建、删除、修改数据库表&…...
安装虚拟机(VMware)保姆级教程及配置虚拟网络编辑器和安装WindowsServer以及宿主机访问虚拟机和配置服务器环境
目录 一、操作系统 1.1.什么是操作系统 1.2.常见操作系统 1.3.个人版本和服务器版本的区别 1.4.Linux的各个版本 二、VMware Wworkstation Pro虚拟机的安装 1.下载与安装 注意:VMWare虚拟网卡 2.配置虚拟网络编辑器 三、安装配置 WindowsServer 1.创建虚拟…...

vue表格列表导出excel
你可以通过下面的步骤使用Vue导出Excel表格: 安装依赖 安装两个依赖包: npm install --save xlsx file-saver创建Excel导出方法 //导出 Excel exportExcel() {// 表格数据let data this.tableData;// 转化为工作簿对象const workbook XLSX.utils.bo…...

CSS基础入门03
目录 1.圆角矩形 1.1基本用法 1.2生成圆形 1.3生成圆角矩形 1.4展开写法 2.Chrome 调试工具--查看 CSS 属性 2.1打开浏览器 2.2标签页含义 2.3elements 标签页使用 3.元素的显示模式 3.1块级元素 3.2行内元素/内联元素 3.3行内元素和块级元素的区别 3.4改变显示模…...

大数据架构设计理论与实践
大数据架构设计理论与实践 大数据处理系统概述 传统数据处理系统存在的问题 大数据处理系统面临的挑战 大数据处理系统的属性/特征 典型的大数据架构 Lambda架构 Lambda定义 优缺点 应用场景 Lambda的体系结构( Batch Layer (批处理层)、Speed Layer (加速层)、Serving Lay…...
)
2024级199管理类联考之英语二2200核心词汇(第三天)
abstract 抽象的,非具体的 n-摘要ideal adj -理想的 n-理想idealized 理想化的ideology 意识形态,思想体系concept 观念,概念 conception n-构想,怀孕,观念awareness 意识,认识significant 重要的,有意义的 significance n-意义,重要性major v-主修 adj-主要的,成年的 n-成年人…...
SQL中:语法总结(group by,having ,distinct,top,order by,like等等)
语法总结:group by,distinct ...... 1.group by2.聚集函数count 3.order by4.增insert、删(drop、delete)、改(update、alter)5.查select嵌套查询不相关子查询相关子查询使用的谓词使用的谓词子查询的相关谓…...

13.计算机视觉
#pic_center R 1 R_1 R1 R 2 R^2 R2 目录 知识框架No.1 数据增广一、数据增广二、D2L代码注意点三、QA No.2 微调一、微调二、D2L代码注意点三、QA No.3 第二次竞赛 树叶分类结果No.4 实战 Kaggle 比赛:图像分类(CIFAR-10)一、Kaggle Cifar…...

关于Java中的运算符
文章目录 前言一、什么是运算符二、算术运算符1.基本四则运算符:加减乘除模( - * / %)2.增量运算符( - * /*)3.自增/自减运算符( --) 三、关系运算符四、逻辑运算符1.逻辑&&2.逻辑||3.逻辑非!4.短路求值 五、位运算六、移位运算七、条件运算符八…...
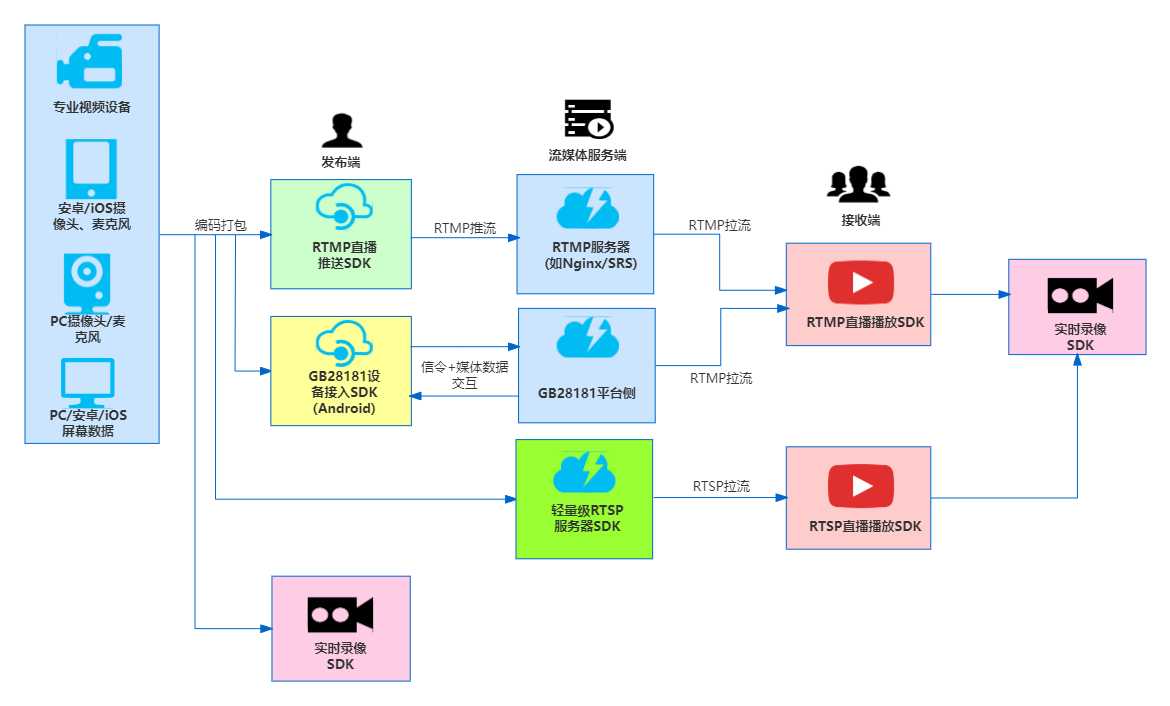
细说RTSP、RTMP和GB28181区别
好多流媒体初学者,对RTSP、RTMP和GB28181三者容易混淆,不了解他们的使用场景和区别,本文抛砖引玉,大概介绍下三者的区别。 RTSP(Real-Time Streaming Protocol)、RTMP(Real-Time Messaging Pro…...
Windows下安装Anaconda、Pycharm以及iflycode插件图解
目录 一、下载Anaconda、Pycharm以及iflycode插件 二、创建相关文件夹 三、Pycharm社区版安装详细步骤 四、Anaconda安装详细步骤 五、配置Pycharm 六、安装iflycode插件 Anaconda是一款集成的Python环境,anaconda可以看做Python的一个集成安装,安…...
Steger算法实现结构光光条中心提取(python版本)
Steger算法原理 对结构光进行光条中心提取时,Steger算法是以Hessian矩阵为基础的。它的基础步骤如下所示: 从Hessian矩阵中求出线激光条纹的法线方向在光条纹法线方向上将其灰度分布按照泰勒多项式展开,求取的极大值即为光条在该法线方向上的亚像素坐标。对于二维离散图像来…...

【完整解题】2023年第四届MathorCup高校数学建模挑战赛——大数据竞赛B题 思路代码文章电商零售商家需求预测及库存优化问题
赛道 B: 电商零售商家需求预测及库存优化问题 问题背景: 电商平台存在着上千个商家,他们会将商品货物放在电商配套的仓库, 电商平台会对这些货物进行统一管理。通过科学的管理手段和智能决策, 大数据智能驱动的供应链可…...

服务网络基础
服务网络基础 目录 前言 从今天开始我们将进入服务网格的学习,服务网格是微服务架构中的一种重要的技术,它可以解决微服务架构中的一些问题,比如服务发现、服务治理、服务监控等等,我们将从服务网格的基础开始,逐步深…...

2016年亚太杯APMCM数学建模大赛C题影视评价与定制求解全过程文档及程序
2016年亚太杯APMCM数学建模大赛 C题 影视评价与定制 原题再现 中华人民共和国成立以来,特别是政治改革和经济开放后,随着国家经济的增长、科技的发展和人民生活水平的提高,中国广播电视媒体取得了显著的成就,并得到了迅速的发展…...

Elasticsearch:使用 Open AI 和 Langchain 的 RAG - Retrieval Augmented Generation (四)
这篇博客是之前文章: Elasticsearch:使用 Open AI 和 Langchain 的 RAG - Retrieval Augmented Generation (一)Elasticsearch:使用 Open AI 和 Langchain 的 RAG - Retrieval Augmented Generation (二&a…...

YOLOv7优化:渐近特征金字塔网络(AFPN)| 助力小目标检测
💡💡💡本文改进:渐近特征金字塔网络(AFPN),解决多尺度削弱了非相邻 Level 的融合效果。 AFPN | 亲测在多个数据集能够实现涨点,尤其在小目标数据集。 收录: YOLOv7高阶自研专栏介绍: http://t.csdnimg.cn/tYI0c ✨✨✨前沿最新计算机顶会复现 🚀🚀🚀…...

J2EE项目部署与发布(Windows版本)
🎬 艳艳耶✌️:个人主页 🔥 个人专栏 :《Spring与Mybatis集成整合》《Vue.js使用》 ⛺️ 越努力 ,越幸运。 1.单机项目的部署 1.1们需要将要进行部署的项目共享到虚拟机中 在部署项目之前,我们先要检查一下…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...

深度解析:etcd 在 Milvus 向量数据库中的关键作用
目录 🚀 深度解析:etcd 在 Milvus 向量数据库中的关键作用 💡 什么是 etcd? 🧠 Milvus 架构简介 📦 etcd 在 Milvus 中的核心作用 🔧 实际工作流程示意 ⚠️ 如果 etcd 出现问题会怎样&am…...
