【LeetCode力扣】189 53 轮转数组 | 最大子数组和
目录
1、189. 轮转数组
1.1、题目介绍
1.2、解题思路
2、53. 最大子数组和
2.1、题目介绍
2.2、解题思路


1、189. 轮转数组
1.1、题目介绍
原题链接:189. 轮转数组 - 力扣(LeetCode)

示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
- 1 <= nums.length <= 10^5
- -2^31 <= nums[ i ] <= (2^31)-1
- 0 <= k <= 10^5
1.2、解题思路
方法一: 使用额外的数组
我们可以使用额外的数组来将每个元素放至正确的位置。用 len 表示数组的长度,我们遍历原数组,将原数组下标为 i 的元素放至新数组下标为 (i+k) % len 的位置,最后将新数组拷贝至原数组即可。
代码实现:
class Solution {public void rotate(int[] nums, int k) {int len = nums.length;int[] tmp = new int[len];for(int i = 0; i < len; i++) {tmp[(i+k)%len] = nums[i];}for(int i = 0; i< len; i++) {nums[i] = tmp[i];}}
}复杂度分析
- 时间复杂度: O(n),其中 n 为数组的长度。
空间复杂度: O(n)。
方法二:整体移动
k = 3 就相当于最右边的3个数整体移到了最左边。

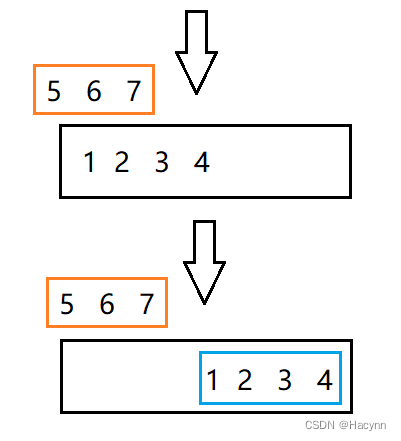

代码实现:
class Solution {public void rotate(int[] nums, int k) {int len = nums.length;int[] tmp = new int[k];k = k % len; //旋转一周等于原来数组,因此首先需要就行k%len操作for(int i = len - k, index = 0; i < len; i++,index++) { //使用tmp数组保存需要旋转的元素tmp[index] = nums[i];}for(int i = len - 1 - k; i >= 0; i--) { //将不需要旋转的元素整体向后移动nums[i + k] = nums[i];}for(int i = 0; i < k; i++) { //将旋转的元素依次放到最前面nums[i] = tmp[i];}}
}复杂度分析 :
- 时间复杂度: O(n),其中 n 为数组的长度。
空间复杂度: O(1),因为只用到了有限空间k。
2、53. 最大子数组和
2.1、题目介绍
原题链接:53. 最大子数组和 - 力扣(LeetCode)

示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
- 1 <= nums.length <= 105
- -104 <= nums[ i ] <= 104
2.2、解题思路
贪心算法:
从头开始对数组进行累加和,当之前的和小于0时,则丢弃之前的和,即将和设为0,再继续结算和,然后和依然小于0,则继续丢弃,同时记录每次算出的最大和。
图解说明:





按照这个规律继续执行,最后可以得出最大和为6,即为答案。
代码实现:
class Solution {public int maxSubArray(int[] nums) {int maxSum = nums[0];int sum = 0;for(int x : nums) {if(sum >= 0) {sum += x;}else{ //贪心思想:如果之前的和小于0,则丢弃之前的和,再重新计算和sum = 0;sum += x;}maxSum = Math.max(maxSum,sum);}return maxSum;}
}复杂度分析:
- 时间复杂度: O(n),只遍历一次数组。
空间复杂度: O(1),只使用了常数空间。
更多【LeetCode刷题】 推荐:
【LeetCode力扣】234 快慢指针 | 反转链表 | 还原链表-CSDN博客![]() https://blog.csdn.net/zzzzzhxxx/article/details/133958602?spm=1001.2014.3001.5502
https://blog.csdn.net/zzzzzhxxx/article/details/133958602?spm=1001.2014.3001.5502
【LeetCode力扣】86. 分隔链表-CSDN博客![]() https://blog.csdn.net/zzzzzhxxx/article/details/133942678?spm=1001.2014.3001.5502
https://blog.csdn.net/zzzzzhxxx/article/details/133942678?spm=1001.2014.3001.5502
【LeetCode力扣】297. 二叉树的序列化与反序列化-CSDN博客![]() https://blog.csdn.net/zzzzzhxxx/article/details/133827375?spm=1001.2014.3001.5502
https://blog.csdn.net/zzzzzhxxx/article/details/133827375?spm=1001.2014.3001.5502

如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!
如果觉得作者写的不错,求给博主一个大大的点赞支持一下,你们的支持是我更新的最大动力!
相关文章:

【LeetCode力扣】189 53 轮转数组 | 最大子数组和
目录 1、189. 轮转数组 1.1、题目介绍 1.2、解题思路 2、53. 最大子数组和 2.1、题目介绍 2.2、解题思路 1、189. 轮转数组 1.1、题目介绍 原题链接:189. 轮转数组 - 力扣(LeetCode) 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3输…...

Go学习第十七章——Gin中间件与路由
Go web框架——Gin中间件与路由 1 单独注册中间件1.1 入门案例1.2 多个中间件1.3 中间件拦截响应1.4 中间件放行 2 全局注册中间件3 自定义参数传递4 路由分组4.1 入门案例4.2 路由分组注册中间件4.3 综合使用 5 使用内置的中间件6 中间件案例权限验证耗时统计 1 单独注册中间件…...

真实感渲染的非正式调研与近期热门研究分享
真实感渲染的非正式调研与近期热门研究分享 1 期刊1 Top2 Venues 2 Rendering Reserach1 Material2 BRDF3 Appearance Modeling4 Capture5 Light Transport光线传播6 Differetiable Rendring-可微渲染7 Ray Tracing8 Denoising降噪9 NeRF 3 VR/AR4 Non-Photorealistic Renderin…...
)
matlab中字符串转换为数字(str2double函数)
str2double函数 将 str 中的文本转换为双精度值。str 包含表示实数或复数值的文本。str 可以是字符向量、字符向量元胞数组或字符串数组。如果 str 是字符向量或字符串标量,则 X 是数值标量。如果 str 是字符向量元胞数组或字符串数组,则 X 是与 str 具…...

基于java的ssm框架农夫果园管理系统设计与实现
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下,你想解决的问…...
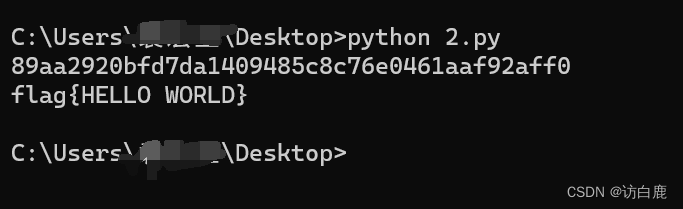
ctf md5爆破
1.知道组成的字符为数字,然后知道加密后的MD5,求组成的字符 import hashlibimport stringdef crackMd5(dst):dst dst.lower()for a in range(0,10):for b in range(0,10):for c in range(0,10):for d in range(0,10):word str(a) str(b) str(c) str(d) "_heetian&q…...

不同碳化硅晶体面带来的可能性
对于非立方晶体,它们天生具有各向异性,即不同方向具有不同的性质。以碳化硅晶体面为例: 4H-SIC和6H-SIC的空间群是P63mc,点群是6mm。两者都属于六方晶系,具有各向异性。3C-SIC的空间群是F-43m,点群是-43m。…...

Kafka集群
Kafka集群 1、Kafka 概述1.1消息队列背景1.2类型1.3Kafka 定义1.4Kafka 简介 2、消息队列好处3、消息队列的模式4、Kafka 的特性5、Kafka 系统架构4、部署 kafka 集群4.1下载安装包4.2 安装 Kafka4.2.1 修改配置文件4.2.2 修改环境变量4.2.3 配置 zookeeper启动脚本4.2.4 设置…...
国腾GM8775C完全替代CS5518 MIPIDSI转2 PORT LVDS
集睿致远CS5518描述: CS5518是一款MIPI DSI输入、LVDS输出转换芯片。MIPI DSI 支持多达4个局域网,每条通道以最 大 1Gbps 的速度运行。LVDS支持18位或24位像素,25Mhz至154Mhz,采用VESA或JEIDA格 式。它只能使用单个1.8v电源&am…...

搜索与图论:匈牙利算法
将所有点分成两个集合,使得所有边只出现在集合之间,就是二分图 二分图:一定不含有奇数个点数的环;可能包含长度为偶数的环, 不一定是连通图 二分图的最大匹配: #include<iostream> #include<cs…...

明星艺人类的百度百科怎么创建 ?
明星艺人们的知名度对于其事业的成功至关重要,而作为国内最大的中文百科全书网站,百度百科成为了人们获取信息的重要来源。一线明星当然百科不用自己操心,平台和网友就给维护了,但是刚刚走红的明星艺人应提早布局百科词条…...

类EMD的“信号分解方法”及MATLAB实现(第八篇)——离散小波变换DWT(小波分解)
在之前的系列文章里,我们介绍了EEMD、CEEMD、CEEMDAN、VMD、ICEEMDAN、LMD、EWT,我们继续补完该系列。 今天要讲到的是小波分解,通常也就是指离散小波变换(Discrete Wavelet Transform, DWT)。在网上有一些介绍该方法…...
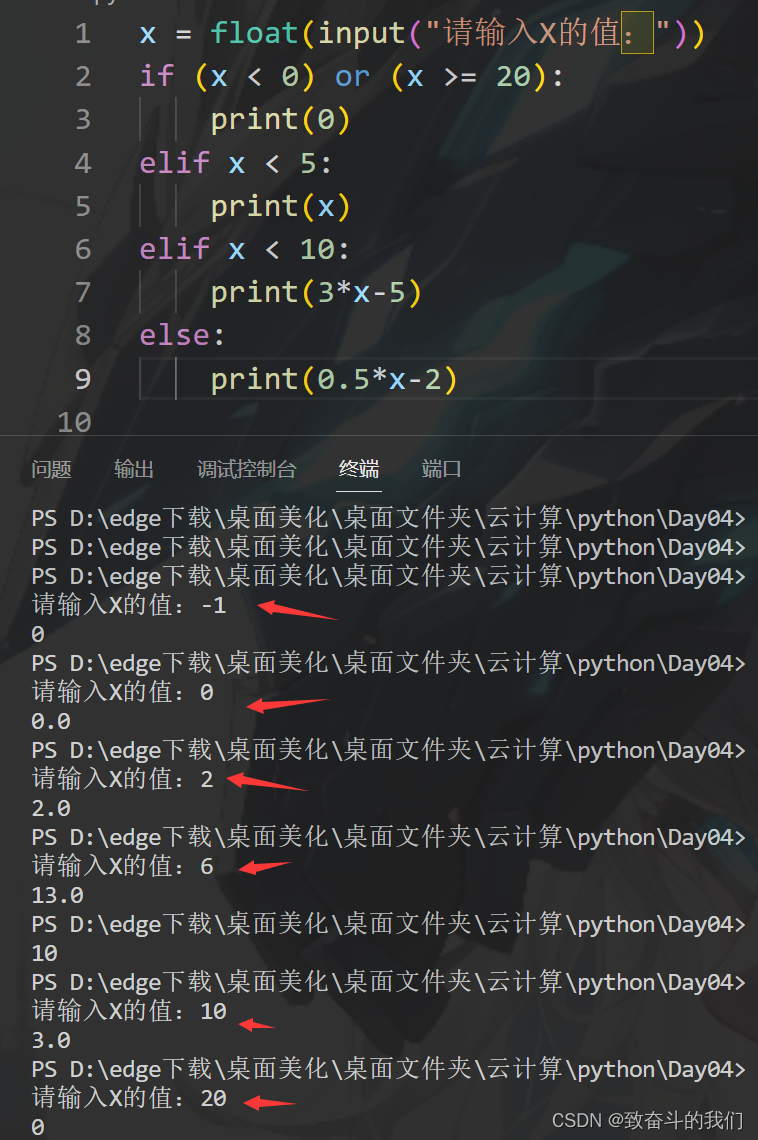
python随手小练10(南农作业题)
题目1: 编写程序,输出1~1000之间所有能被4整除,但是不能被5整除的数 具体操作: for i in range(1,1000): #循环遍历1~999,因为range是左闭右开if (i % 4 0) and (i % 5 ! 0) :print(i) 结果展示: 题目2&…...

How to install mongodb-7.0 as systemd service with podman
How to install mongodb-7.0 as systemd service with podman 1、安装1.1、创建卷1.2、配置文件1.3、创建容器1.4、服务管理1.5、容器管理 2、客户端管理 1、安装 1.1、创建卷 配置卷 podman volume create --label typemongo-7.0 --label envdev mongo-7.0-conf数据卷 pod…...

一文彻底理解python浅拷贝和深拷贝
目录 一、必备知识二、基本概念三、列表,元组,集合,字符串,字典浅拷贝3.1 列表3.2 元组3.3 集合3.4 字符串3.5 字典3.6 特别注意浅拷贝总结 四、列表,元组,集合,字符串,字典深拷贝 一…...

什么是软件的生命周期?全方位解释软件的生命周期
软件的生命周期 软件生命周期是指从软件产品的设想开始到软件不再使用而结束的时间。 如果把软件看成是有生命的事 物,那么软件的生命周期可以分成6个阶段,即需求分析、计划、设计、编码、测试、运行维护 需求分析阶段: 分析需求的可行性&…...

网络安全—小白自学
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟…...

List 3.5 详解原码、反码、补码
前言 欢迎来到我的博客,我是雨空集(全网同名),无论你是无意中发现我,还是有意搜索而来,我都感到荣幸。这里是一个分享知识、交流想法的平台,我希望我的博客能给你带来帮助和启发。如果你喜欢我…...

数据清洗与规范化详解
数据处理流程,也称数据处理管道,是将原始数据转化为有意义的信息和知识的一系列操作步骤。它包括数据采集、清洗、转换、分析和可视化等环节,旨在提供有用的见解和决策支持。在数据可视化中数据处理是可视化展示前非常重要的一步,…...

Ansible playbook的block
环境 控制节点:Ubuntu 22.04Ansible 2.10.8管理节点:CentOS 8 block 顾名思义,通过block可以把task按逻辑划分到不同的“块”里面,实现“块操作”。此外,block还提供了错误处理功能。 task分组 下面的例子&#x…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

RabbitMQ 各类交换机
为什么要用交换机? 交换机用来路由消息。如果直发队列,这个消息就被处理消失了,那别的队列也需要这个消息怎么办?那就要用到交换机 交换机类型 1,fanout:广播 特点 广播所有消息:将消息…...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
