折半搜索(meet in the middle)
介绍
折半搜索,又称 meet in the middle \text{meet in the middle} meet in the middle,指将整个搜索过程分为两部分,并对两部分分别进行搜索,最后得到两个答案序列,将这两个答案序列进行合并,即可得到最终的答案。
这样做的目的是降低时间复杂度。举个例子,如果每层搜索都有两种选择,那么时间复杂度是 O ( 2 n ) O(2^n) O(2n)的。如果我们用折半搜索,那时间复杂度就降为 O ( 2 n / 2 + k ) O(2^{n/2}+k) O(2n/2+k),其中 k k k指将两个答案序列合并的时间复杂度。
例题
洛谷P4799 [CEOI2015 Day2] 世界冰球锦标赛
题目大意
有 n n n场比赛,第 i i i场比赛的门票的价格为 a i a_i ai。 Bobek \text{Bobek} Bobek有 m m m元钱,问他有多少种不同的观赛方案。
1 ≤ n ≤ 40 , 1 ≤ m ≤ 1 0 18 , 1 ≤ a i ≤ 1 0 16 1\leq n\leq 40,1\leq m\leq 10^{18},1\leq a_i\leq 10^{16} 1≤n≤40,1≤m≤1018,1≤ai≤1016
题解
我们首先可以想到的是用状压枚举每一种情况,但这样的时间复杂度为 O ( 2 n ) O(2^n) O(2n),会 TLE \text{TLE} TLE。
我们考虑用折半搜索解决问题。
先将所有比赛分为两部分,分别求出两个部分中所有可能的观赛方案的花费。那么,我们在前一部分中取方案 a a a,后一部分中取方案 b b b,则只有满足方案 a a a和方案 b b b的花费之和小于等于 m m m,这两种方案才会对答产生贡献。
那么,我们用一个数组 w w w记录前一部分的每种方案的花费,然后将 w w w从小到大排序。对于后一部分的每种方案的花费 t t t,我们在 w w w中二分求所有满足花费小于等于 m − t m-t m−t的观赛方案数量,再将其贡献在答案中即可。
求出 w w w并排序的时间复杂度为 O ( n 2 n / 2 ) O(n2^{n/2}) O(n2n/2),求出每个 t t t并二分查找的时间复杂度为 O ( n 2 n / 2 ) O(n2^{n/2}) O(n2n/2),所以总时间复杂度为 O ( n 2 n / 2 ) O(n2^{n/2}) O(n2n/2)。
code
#include<bits/stdc++.h>
using namespace std;
int n,w1=0;
long long m,now,ans=0,a[45],w[1<<20];
int main()
{scanf("%d%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);}for(int s=0;s<1<<(n/2);s++){w[++w1]=0;for(int i=1;i<=n/2;i++){if((s>>i-1)&1) w[w1]+=a[i];}}sort(w+1,w+w1+1);for(int s=0;s<1<<(n-n/2);s++){now=0;for(int i=1;i<=n-n/2;i++){if((s>>i-1)&1) now+=a[n/2+i];}ans+=upper_bound(w+1,w+w1+1,m-now)-w-1;}printf("%lld",ans);return 0;
}
相关文章:
)
折半搜索(meet in the middle)
介绍 折半搜索,又称 meet in the middle \text{meet in the middle} meet in the middle,指将整个搜索过程分为两部分,并对两部分分别进行搜索,最后得到两个答案序列,将这两个答案序列进行合并,即可得到最…...
【机器学习】loss损失讨论
大纲 验证集loss上升,准确率也上升(即将overfitting?)训练集loss一定为要为0吗 Q1. 验证集loss上升,准确率也上升 随着置信度的增加,一小部分点的预测结果是错误的(log lik 给出了指数级的惩…...

LeetCode 779. 第K个语法符号【递归,找规律,位运算】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
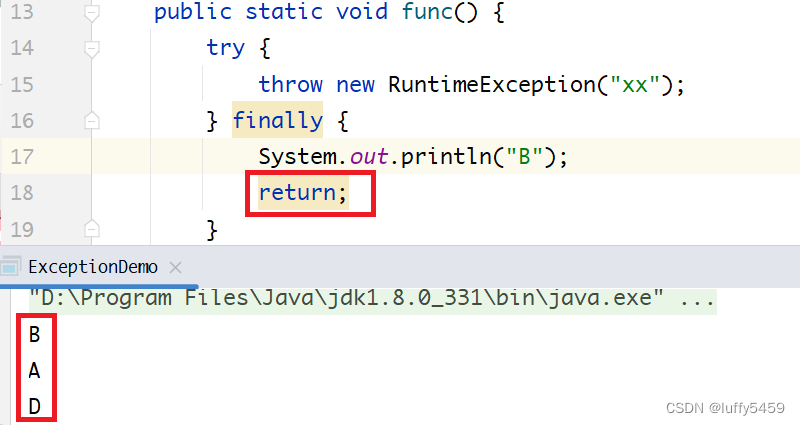
java try throw exception finally 遇上 return break continue造成异常丢失
如下所示,是一个java笔试题,考察的是抛出异常之后,程序运行结果,但是这里抛出异常,并没有捕获异常,而是通过finally来进行了流程控制处理。 package com.xxx.test;public class ExceptionFlow {public sta…...
+ Spring相关源码)
设计模式——装饰器模式(Decorator Pattern)+ Spring相关源码
文章目录 一、装饰器模式的定义二、个人理解举个抽象的例(可能并不是很贴切) 三、例子1、菜鸟教程例子1.1、定义对象1.2、定义装饰器 3、JDK源码 ——包装类4、JDK源码 —— IO、OutputStreamWriter5、Spring源码 —— BeanWrapperImpl5、SpringMVC源码 …...
MATLAB R2018b详细安装教程(附资源)
云盘链接: pan.baidu.com/s/1SsfNtlG96umfXdhaEOPT1g 提取码:1024 大小:11.77GB 安装环境:Win10/Win8/Win7 安装步骤: 1.鼠标右击【R2018b(64bit)】压缩包选择【解压到 R2018b(64bit)】 2.打开解压后的文件夹中的…...
GEE错误——影像加载过程中出现的图层无法展示的解决方案
问题: // I dont know if some standard value exists for the radius, in the same, I will assume that some software would prefer to use square shape, but circle makes more sense to me. // pixels is noice if you want to zoom in and out to visualize…...
读图数据库实战笔记03_遍历
1. Gremlin Server只将数据存储在内存中 1.1. 如果停止Gremlin Server,将丢失数据库里的所有数据 2. 概念 2.1. 遍历(动词) 2.1.1. 当在图数据库中导航时,从顶点到边或从边到顶点的移动过程 2.1.2. 类似于在关系数据库中的查…...

QT如何检测当前系统是是Windows还是Uninx或Mac?以及是哪个版本?
简介 通过Qt获取当前系统及版本号,需要用到QSysInfo。 QSysInfo类提供有关系统的信息。 WordSize指定了应用程序编译所在的平台的指针大小。 ByteOrder指定了平台是大端序还是小端序。 某些常量仅在特定的平台上定义。您可以使用预处理器符号Q_OS_WIN和Q_OS_MACOS来…...
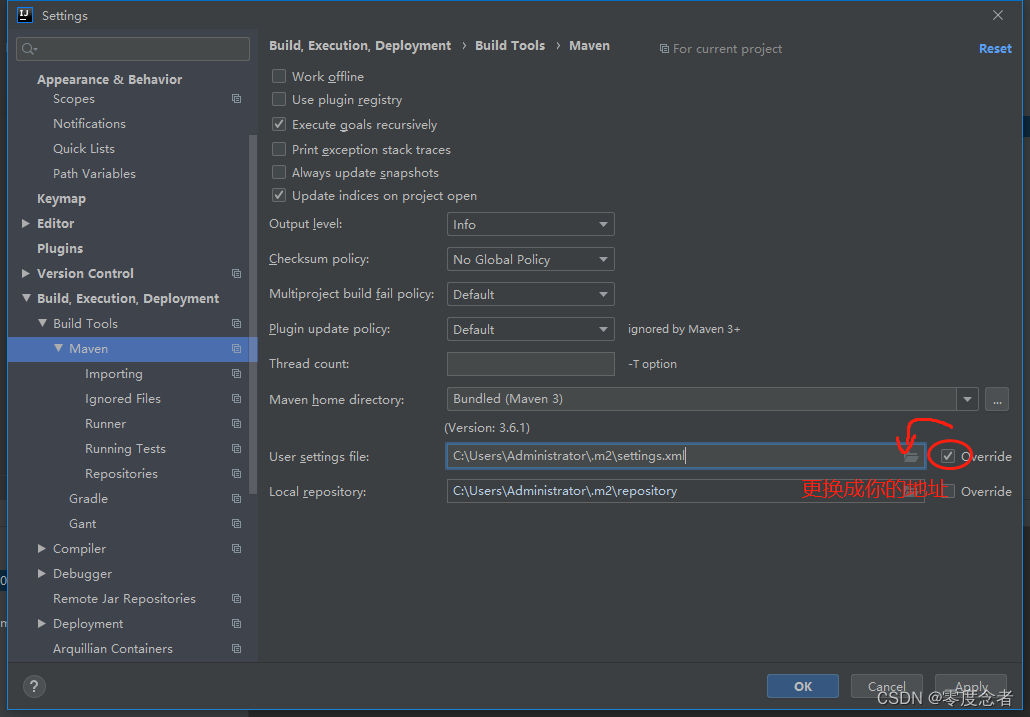
Maven配置阿里云中央仓库settings.xml
Maven配置阿里云settings.xml 前言一、阿里云settings.xml二、使用步骤1.任意目录创建settings.xml2.使用阿里云仓库 总结 前言 国内网络从maven中央仓库下载文件通常是比较慢的,所以建议配置阿里云代理镜像以提高jar包下载速度,IDEA中我们需要配置自己…...

由浅入深C系列八:如何高效使用和处理Json格式的数据
如何高效使用和处理JSON格式的数据 问题引入关于CJSON示例代码头文件引用处理数据 问题引入 最近的项目在用c处理后台的数据时,因为好多外部接口都在使用Json格式作为返回的数据结构和数据描述,如何在c中高效使用和处理Json格式的数据就成为了必须要解决…...
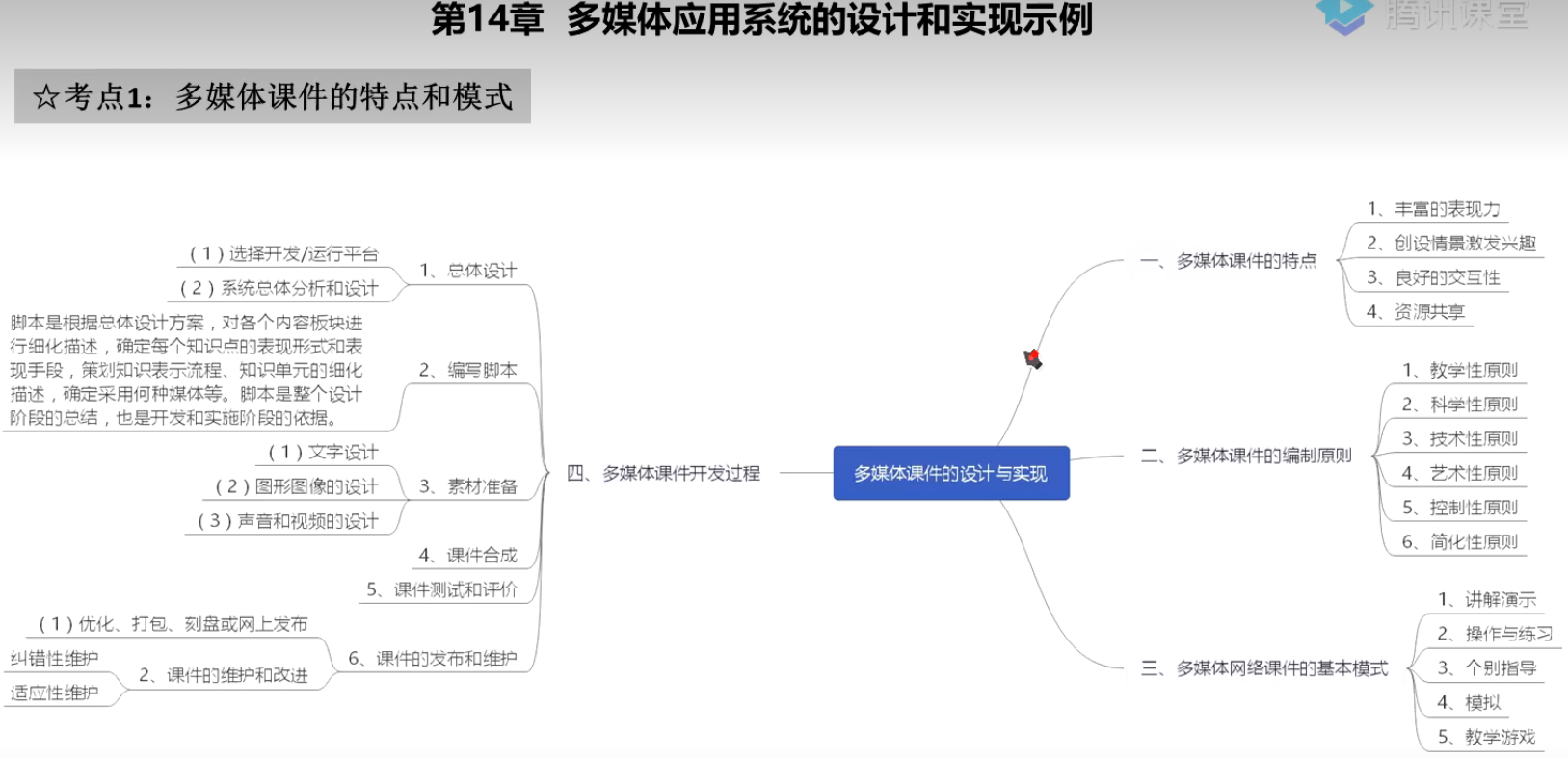
多媒体应用设计师 第16章 多媒体应用系统的设计和实现示例
口诀 思维导图 2020...

golang平滑重启库overseer实现原理
overseer主要完成了三部分功能: 1、连接的无损关闭,2、连接的平滑重启,3、文件变更的自动重启。 下面依次讲一下: 一、连接的无损关闭 golang官方的net包是不支持连接的无损关闭的,当主监听协程退出时,…...
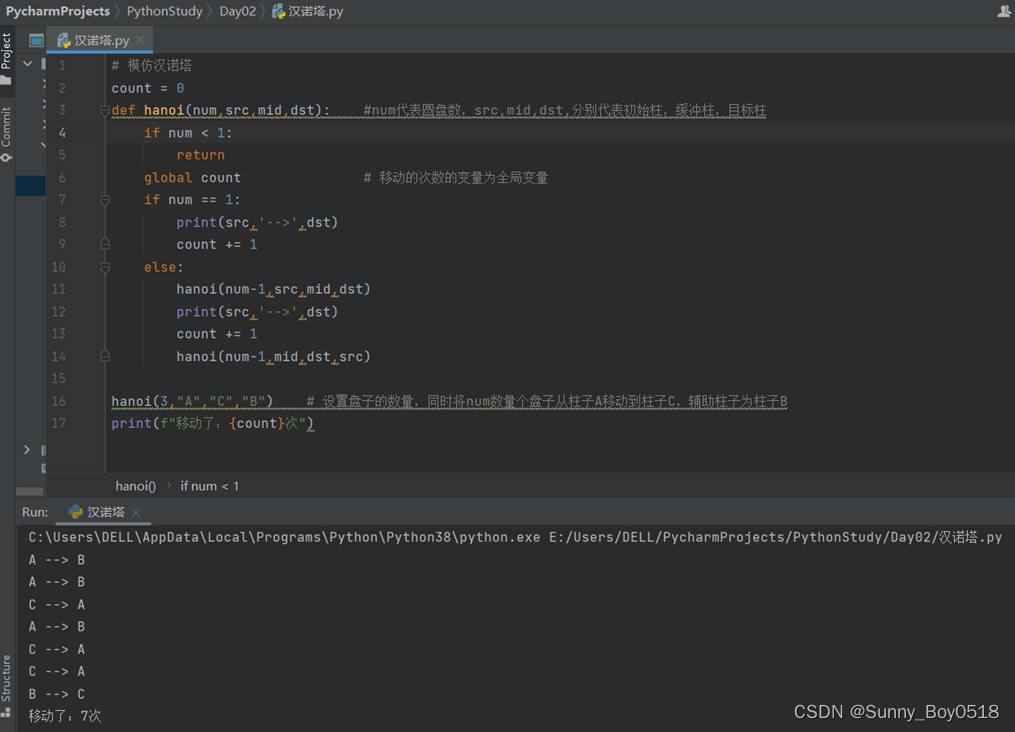
用Python定义一个函数,用递归的方式模拟汉诺塔问题
【任务需求】 定义一个函数,用递归的方式模拟汉诺塔问题,三个柱子,分别为A、B、C,其中A柱子上有N个盘子,从小到大编号为1到N,盘子大小不同。现在要将这N个盘子从A柱子移动到C柱子上,但移动的过…...

二手的需求
案例1030 某天项目经理小王,从用户现场带回了需求,以图形的方式,交给了产品经理。告诉他就照这样设计,结果是项目经理放弃让产品经理出效果图。 原因是产品经理觉得项目经理带回来的需求有问题。项目经理解释产品经理不接受&…...
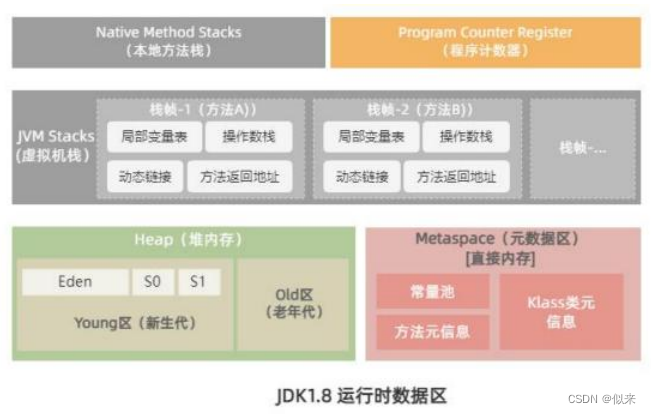
大厂面试题-JVM为什么使用元空间替换了永久代?
目录 面试解析 问题答案 面试解析 我们都知道Java8以及以后的版本中,JVM运行时数据区的结构都在慢慢调整和优化。但实际上这些变化,对于业务开发的小伙伴来说,没有任何影响。 因此我可以说,99%的人都回答不出这个问题。 但是…...
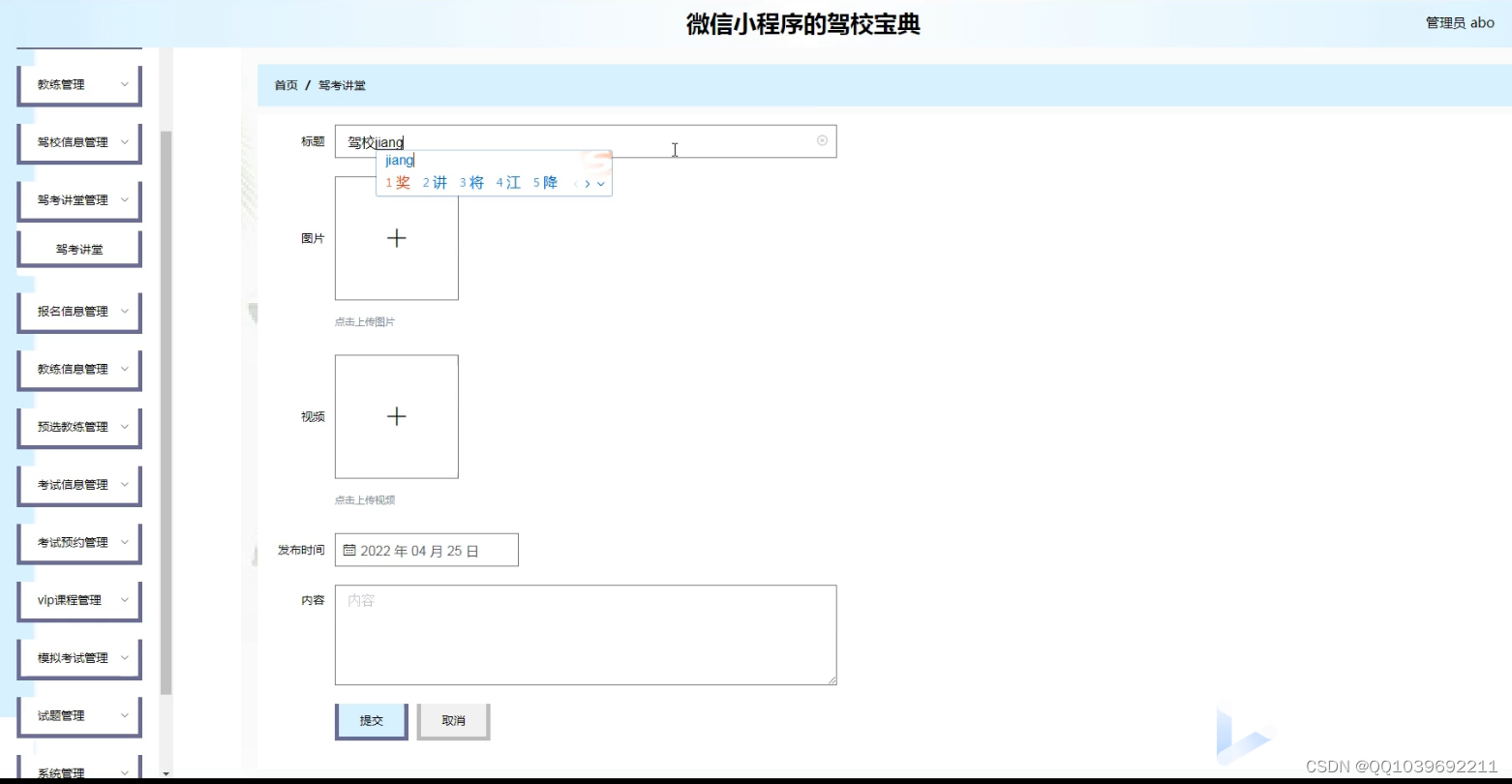
基本微信小程序的驾校宝典系统-驾照考试系统
项目介绍 系统模块分析是对系统的各个模块做出相应的说明以及解释。此系统的模块分别有用户模块、服务端模块和管理端模块这两大基本模块,其中服务端模块包括了首页、教练信息、教练咨讯、考试预约、我的等;而管理端模块则包括了个人中心、用户管理、教…...
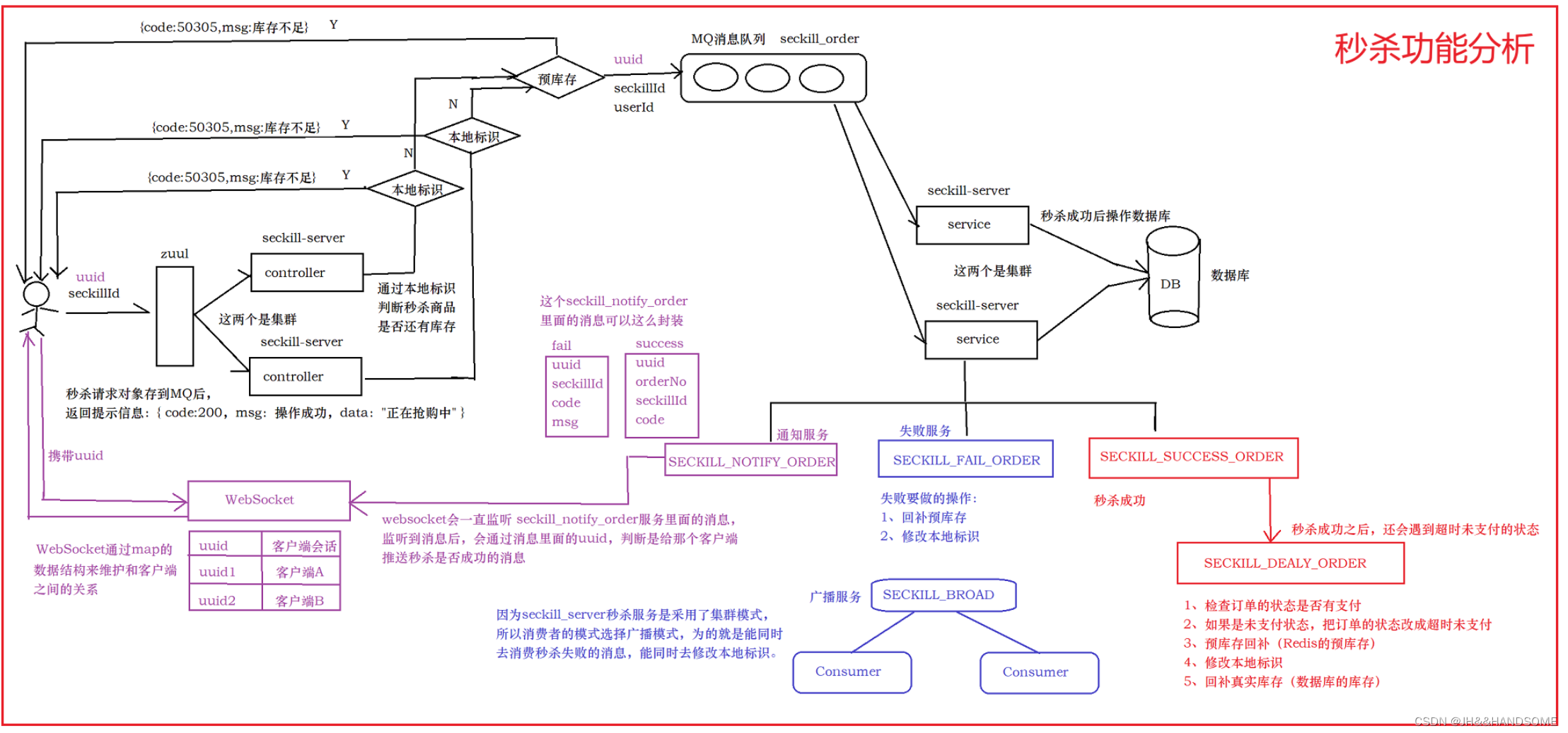
02、SpringCloud -- Redis和Cookie过期时间刷新功能
目录 需求:代码流程过滤器类工具类过滤判断远程调用feign接口gitee 配置接口实现过滤器run方法测试:问题:秒杀功能完整分析图 需求: cookie应该写在网关中,网关中可以自定义filter过滤器,用来实现cookie的刷新和redis中key的刷新,延长用户的操作时间。 就是让用户每操…...

【报错】kali安装ngrok报错解决办法(zsh: exec format error: ./ngrok)
问题描述 kali安装ngrok令牌授权失败 在安装配置文件的时候报错:zsh: exec format error: ./ngrok 原因分析: 在Kali Linux上执行./ngrok时出现zsh exec格式错误的问题可能是由于未安装正确版本的ngrok或操作系统不兼容ngrok导致的。以下是一些可能的解…...

<学习笔记>从零开始自学Python-之-常用库篇(十三)内置小型数据库shelve
一、shelve简介: shelve是Python当中数据储存的方案,类似key-value数据库,便于保存Python对象,shelve只有一个open()函数,用来打开指定的文件(字典),会返回一…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
