轨迹规划 | 图解路径跟踪PID算法(附ROS C++/Python/Matlab仿真)
目录
- 0 专栏介绍
- 1 PID控制基本原理
- 2 基于PID的路径跟踪
- 3 仿真实现
- 3.1 ROS C++实现
- 3.2 Python实现
- 3.3 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 PID控制基本原理
PID控制是一种常用的经典控制算法,其应用背景广泛,例如
- 工业自动化控制:温度控制、压力控制、流量控制、液位控制等过程控制系统多采用PID闭环,可以帮助维持系统参数在设定值附近,以提高生产过程的稳定性和效率;
- 机械工程:PID算法可用于实现精确的运动控制,包括控制位置、速度和力。这包括机器人控制、电机控制、汽车巡航控制等;
- 农业自动化:PID算法可用于控制温室环境,包括温度、湿度和光照,以促进植物的生长和提高农业生产;
- …
PID代表比例(Proportional)、积分(Integral)和微分(Derivative),它通过根据误差信号的大小和变化率来调整控制器的输出,以使系统的输出尽可能接近期望值,其控制框图如下所示

连续型PID控制律如下
u ( t ) = K p e ( t ) + K i ∫ t 0 t e ( τ ) d τ + K d e ˙ ( t ) u\left( t \right) =K_pe\left( t \right) +K_i\int_{t_0}^t{e\left( \tau \right) \mathrm{d}\tau}+K_d\dot{e}\left( t \right) u(t)=Kpe(t)+Ki∫t0te(τ)dτ+Kde˙(t)
其中 K p K_p Kp、 K i K_i Ki、 K d K_d Kd分别称为比例、积分与微分增益系数
位置式离散型PID控制律如下
u ( k ) = K p e ( k ) + K i ∑ i = 0 k e ( i ) Δ t + K d ( e ( k ) − e ( k − 1 ) ) / Δ t u\left( k \right) =K_pe\left( k \right) +K_i\sum_{i=0}^k{e\left( i \right) \varDelta t}+K_d{{\left( e\left( k \right) -e\left( k-1 \right) \right)}/{\varDelta t}} u(k)=Kpe(k)+Kii=0∑ke(i)Δt+Kd(e(k)−e(k−1))/Δt
由于位置式PID算法需要计算累计偏差,占用存储单元,可以通过
u ( k ) − u ( k − 1 ) u\left( k \right) -u\left( k-1 \right) u(k)−u(k−1)
计算增量式PID控制律
Δ u ( k ) = K p Δ e ( k ) + K i e ( k ) Δ t + K d ( Δ e ( k ) − Δ e ( k − 1 ) ) / Δ t \varDelta u\left( k \right) =K_p\varDelta e\left( k \right) +K_ie\left( k \right) \varDelta t+K_d{{\left( \varDelta e\left( k \right) -\varDelta e\left( k-1 \right) \right)}/{\varDelta t}} Δu(k)=KpΔe(k)+Kie(k)Δt+Kd(Δe(k)−Δe(k−1))/Δt
其中
Δ u ( k ) = u ( k ) − u ( k − 1 ) Δ e ( k ) = e ( k ) − e ( k − 1 ) \varDelta u\left( k \right) =u\left( k \right) -u\left( k-1 \right) \\ \varDelta e\left( k \right) =e\left( k \right) -e\left( k-1 \right) Δu(k)=u(k)−u(k−1)Δe(k)=e(k)−e(k−1)
2 基于PID的路径跟踪
在基于PID的局部路径规划中,希望机器人能快速跟踪上预设的轨迹,设误差量为 e k e_k ek。 e k e_k ek可以根据实际的控制目标进行选择,例如线速度误差、角速度误差、轨迹跟踪误差等
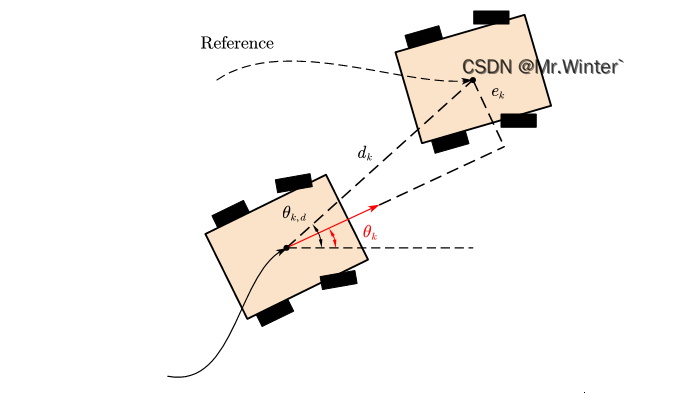
以轨迹跟踪误差为例,如图所示,根据几何关系可得
e k = sin ( θ k , d − θ k ) ⋅ d k e_k=\sin \left( \theta _{k,d}-\theta _k \right) \cdot d_k ek=sin(θk,d−θk)⋅dk
其中
θ k , d = a tan ( y k , d − y k , x k , d − x k ) d k = ( x k , d − x k ) 2 + ( y k , d − y k ) 2 \theta _{k,d}=\mathrm{a}\tan \left( y_{k,d}-y_k,x_{k,d}-x_k \right) \\ d_k=\sqrt{\left( x_{k,d}-x_k \right) ^2+\left( y_{k,d}-y_k \right) ^2} θk,d=atan(yk,d−yk,xk,d−xk)dk=(xk,d−xk)2+(yk,d−yk)2
接着以该误差作为反馈测量值通过PID控制器生成控制量,机器人基于控制量和运动学模型运动,循环往复直到机器人完成控制目标
3 仿真实现
3.1 ROS C++实现
核心的线速度PID控制和角速度PID控制代码如下
double PIDPlanner::LinearPIDController(nav_msgs::Odometry& base_odometry, double b_x_d, double b_y_d)
{double v = std::hypot(base_odometry.twist.twist.linear.x, base_odometry.twist.twist.linear.y);double v_d = std::hypot(b_x_d, b_y_d) / d_t_;if (std::fabs(v_d) > max_v_)v_d = std::copysign(max_v_, v_d);double e_v = v_d - v;i_v_ += e_v * d_t_;double d_v = (e_v - e_v_) / d_t_;e_v_ = e_v;double v_inc = k_v_p_ * e_v + k_v_i_ * i_v_ + k_v_d_ * d_v;if (std::fabs(v_inc) > max_v_inc_)v_inc = std::copysign(max_v_inc_, v_inc);double v_cmd = v + v_inc;if (std::fabs(v_cmd) > max_v_)v_cmd = std::copysign(max_v_, v_cmd);else if (std::fabs(v_cmd) < min_v_)v_cmd = std::copysign(min_v_, v_cmd);return v_cmd;
}
double PIDPlanner::AngularPIDController(nav_msgs::Odometry& base_odometry, double e_theta)
{regularizeAngle(e_theta);double w_d = e_theta / d_t_;if (std::fabs(w_d) > max_w_)w_d = std::copysign(max_w_, w_d);double w = base_odometry.twist.twist.angular.z;double e_w = w_d - w;i_w_ += e_w * d_t_;double d_w = (e_w - e_w_) / d_t_;e_w_ = e_w;double w_inc = k_w_p_ * e_w + k_w_i_ * i_w_ + k_w_d_ * d_w;if (std::fabs(w_inc) > max_w_inc_)w_inc = std::copysign(max_w_inc_, w_inc);double w_cmd = w + w_inc;if (std::fabs(w_cmd) > max_w_)w_cmd = std::copysign(max_w_, w_cmd);else if (std::fabs(w_cmd) < min_w_)w_cmd = std::copysign(min_w_, w_cmd);return w_cmd;
}

3.2 Python实现
主体控制流程如下:
def plan(self):plan_idx = 0for _ in range(self.max_iter):# break until goal reachedif math.hypot(self.robot.px - self.goal[0], self.robot.py - self.goal[1]) < self.p_precision:return True, self.robot.history_pose# find next tracking pointwhile plan_idx < len(self.path):...# calculate velocity commandif math.hypot(self.robot.px - self.goal[0], self.robot.py - self.goal[1]) < self.p_precision:if abs(self.robot.theta - self.goal[2]) < self.o_precision:u = np.array([[0], [0]])else:u = np.array([[0], [self.angularController(self.goal[2])]])elif abs(theta_d - self.robot.theta) > np.pi / 2:u = np.array([[0], [self.angularController(theta_d)]])else:v_d = math.hypot(b_x_d, b_y_d) / self.dt / 10u = np.array([[self.linearController(v_d)], [self.angularController(theta_d)]])# feed into robotic kinematicself.robot.kinematic(u, self.dt)return False, None

3.3 Matlab实现
核心的线速度PID控制和角速度PID控制代码如下
function [v, e_v_, i_v_] = linearController(robot, b_x_d, b_y_d, dt, e_v_, i_v_)v_d = norm([b_x_d, b_y_d]) / dt / 10;e_v = v_d - robot.v;i_v_ = i_v_ + e_v * dt;d_v = (e_v - e_v_) / dt;e_v_ = e_v;k_v_p = 1.00;k_v_i = 0.00;k_v_d = 0.00;v_inc = k_v_p * e_v_ + k_v_i * i_v_ + k_v_d * d_v;v = robot.v + v_inc;
end
function [w, e_w_, i_w_] = angularController(robot, theta_d, dt, e_w_, i_w_)e_theta = theta_d - robot.theta;if (e_theta > pi)e_theta = e_theta - 2 * pi;elseif (e_theta < -pi)e_theta = e_theta + 2 * pi;endw_d = e_theta / dt / 10;e_w = w_d - robot.w;i_w_ = i_w_ + e_w * dt;d_w = (e_w - e_w_) / dt;e_w_ = e_w;k_w_p = 1.00;k_w_i = 0.00;k_w_d = 0.01;w_inc = k_w_p * e_w_ + k_w_i * i_w_ + k_w_d * d_w;w = robot.w + w_inc;
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

轨迹规划 | 图解路径跟踪PID算法(附ROS C++/Python/Matlab仿真)
目录 0 专栏介绍1 PID控制基本原理2 基于PID的路径跟踪3 仿真实现3.1 ROS C实现3.2 Python实现3.3 Matlab实现 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等)&a…...
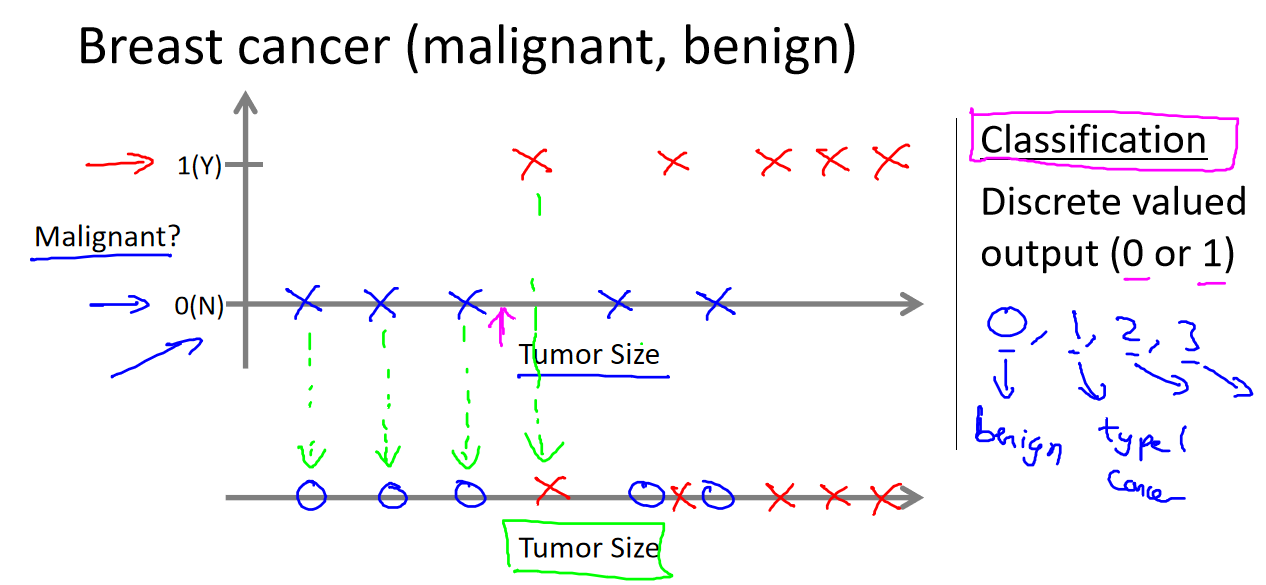
吴恩达《机器学习》1-3:监督学习
一、监督学习 例如房屋价格的数据集。在监督学习中,我们将已知的房价作为"正确答案",并将这些价格与房屋的特征数据一起提供给学习算法。学习算法使用这些已知答案的数据来学习模式和关系,以便在未知情况下预测其他房屋的价格。这就…...

Flutter PopupMenuButton下拉菜单
下拉菜单是移动应用交互中一种常见的交互方式,可以使用下拉列表来展示多个内容标签,实现页面引导的作用。在Flutter开发中,实现下拉弹框主要有两种方式,一种是继承Dialog组件使用自定义布局的方式实现,另一种则是使用官方的PopupMenuButton组件进行实现。 如果没有特殊的…...

国家数据局正式揭牌,数据专业融合型人才迎来发展良机【文末送书五本】
国家数据局正式揭牌,数据专业融合型人才迎来发展良机 国家数据局正式揭牌,数据专业融合型人才迎来发展良机 摘要书籍简介数据要素安全流通Python数据挖掘:入门、进阶与实用案例分析数据保护:工作负载的可恢复性Data Mesh权威指南分…...
H5游戏源码分享-像素小鸟游戏(类似深海潜艇)
H5游戏源码分享-像素小鸟游戏(类似深海潜艇) 点击屏幕控制小鸟的飞行高度 整个小游戏就用JS完成 项目地址:https://download.csdn.net/download/Highning0007/88483228 <!DOCTYPE HTML> <html><head><meta http-equiv…...

Vue 3 响应式对象:ref 和 reactive 的使用和区别
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是尘缘,一个在CSDN分享笔记的博主。📚📚 👉点击这里,就可以查看我的主页啦!👇&#x…...

H5游戏源码分享-密室逃脱小游戏(考验反应能力)
H5游戏源码分享-密室逃脱小游戏(考验反应能力) 预判安全位置,这个需要快速的反应能力 源码 <!DOCTYPE html> <html> <head> <meta http-equiv"Content-Type" content"text/html; charsetutf-8" /&…...
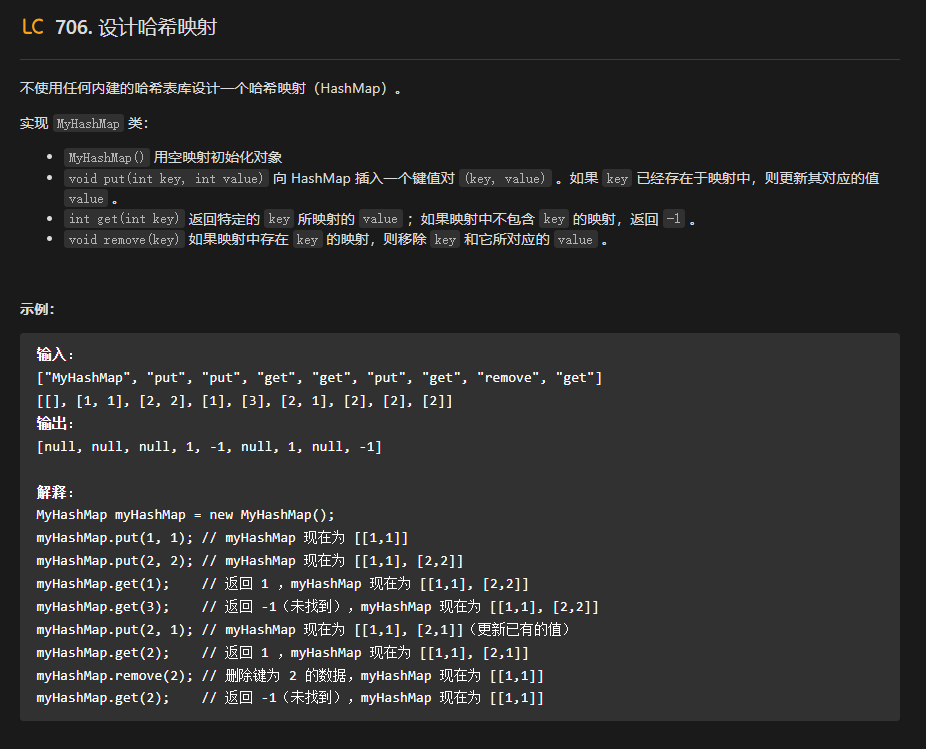
【LeetCode刷题-哈希】--706.设计哈希映射
706.设计哈希映射 class MyHashMap {private class Pair{private int key;private int value;public Pair(int key ,int value){this.key key;this.value value;}public int getKey(){return key;}public int getValue(){return value;}public void setValue(int value){this…...
前端 : 用HTML ,CSS ,JS 做一个点名器
1.HTML: <body><div id "content"><div id"top"><div id "name">XAiot2302班点名器</div></div><div id "center"><div id "word">你准备好了吗?</di…...
css:button实现el-radio效果
先看最终效果: 思路: 一、 首先准备好按钮内容:const a [one,two,three] 将按钮循环展示出来,并设置一些样式,将按钮背景透明: <button v-for"(item,index) in a" :key"in…...

算法工程师-机器学习-数据科学家面试准备4-ML系统设计
https://github.com/LongxingTan/Machine-learning-interview 算法工程师-机器学习-数据科学家面试准备1- 概述 外企和国外公司、春招、秋招算法工程师-机器学习-数据科学家面试准备2- Leetcode 300算法工程师-机器学习-数据科学家面试准备3-系统设计算法工程师-机器学习-数据…...
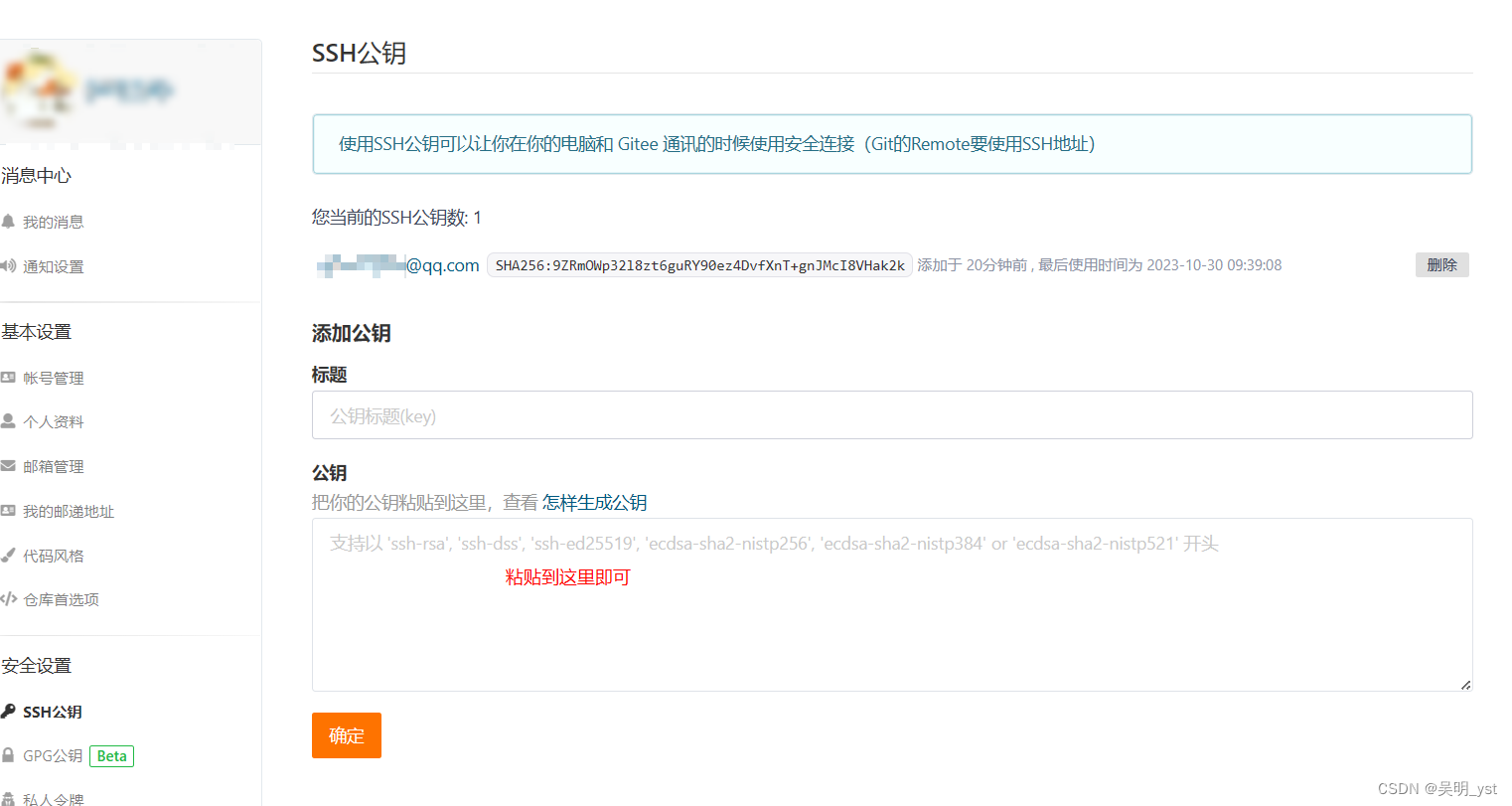
git重装后如何连接以前项目
git重装后如何连接以前项目 1、配置秘钥 点击 Git Bash Here,进入命令操作窗口 生成本地git仓库秘钥: 1、填写自己邮箱 2、一直回车 ssh-keygen -t rsa -C “xxxxxqq.com”3、使用cat查看生成的秘钥,粘贴并设置到gitee上 cat ~/.ssh/id_r…...
【java学习—十】TreeSet集合(5)
文章目录 1. TreeSet1.1. 自然排序1.2. 定制排序 1. TreeSet TreeSet 是 SortedSet 接口的实现类, TreeSet 可以确保集合元素处于排序状态。 TreeSet 支持两种排序方法:自然排序和定制排序。默认情况下, TreeSet 采用自然排序。 1.1.…...
JMeter的使用,傻瓜式学习【上】
目录 前言 1、JMeter元件及基本使用作用域(简述) 1.1、基本元件 1.2、作用域的原则 1.3、元件执行顺序 3、JMeter三个重要组件 3.1、线程组 案例: 3.2、HTTP请求 3.3、查看结果树 响应体中,中文乱码解决方案࿱…...
)
主定理(一般式)
主定理(Master Theorem)是用于分析递归算法时间复杂度的一个重要工具。它适用于形式化定义的一类递归关系,通常采用分治策略解决问题的情况。 目录 主定理简化版的局限主定理一般形式情况1: n l o g b a n^{log_{b}{a}} nlogba …...
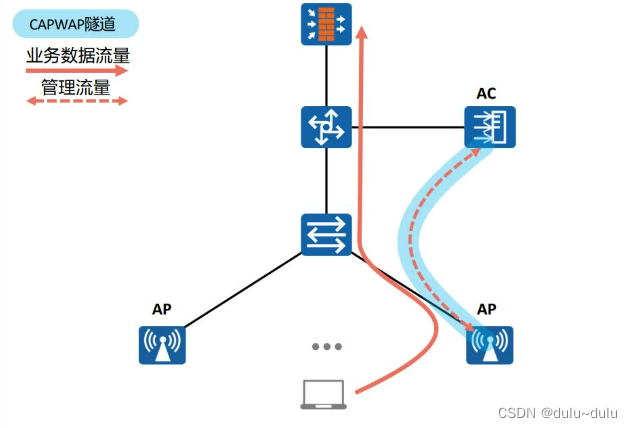
WLAN的组网架构和工作原理
目录 WLAN的组网架构 FAT AP架构 AC FIT AP架构 敏捷分布式AP 下一代园区网络:智简园区(大中型园区网络) WLAN工作原理 WLAN工作流程 1.AP上线 (1)AP获取IP地址; (2)AP发…...
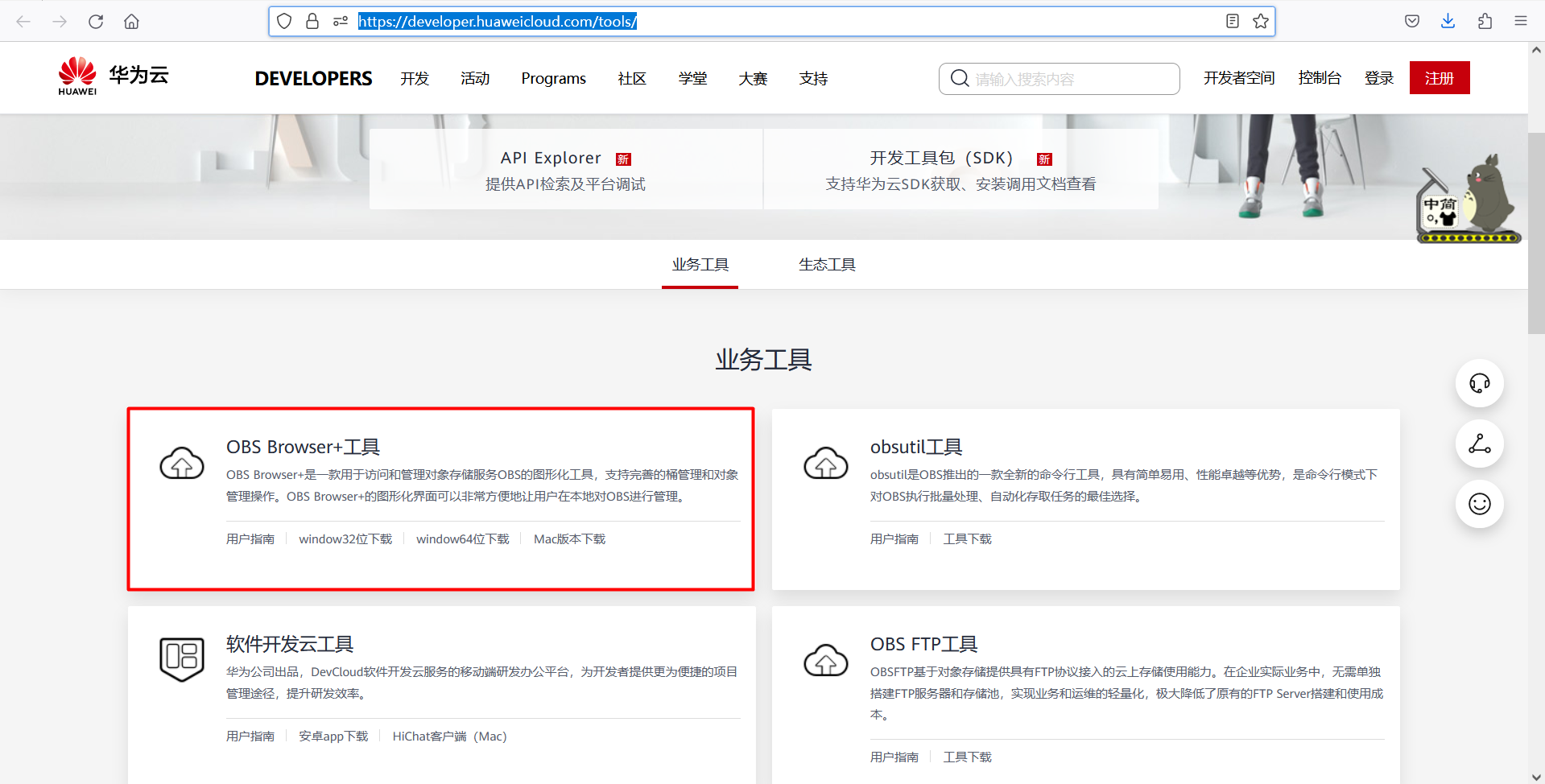
使用OBS Browser+访问华为云OBS存储【Windows】
背景 项目中使用华为云 S3 存储,java 代码中通过华为云 OBS 提供的esdk-obs-java 来访问文件。 但是,通过 JAVA SDK 方式不太方便运维,所以我们需要一款可视化的客户端软件。 华为云 OBS 自身也提供了一款客户端软件,名为 OBS Browser+。 OBS Browser+简介 OBS Browse…...
:类的动态内存分配、异常、类型转换运算符)
C++总结(3):类的动态内存分配、异常、类型转换运算符
文章目录 1 类的动态内存分配1.1 C动态内存分配1.2 拷贝构造函数1.3 赋值运算符(operator)重载 2 异常3 类型转换运算符 1 类的动态内存分配 1.1 C动态内存分配 在C/C中都可以使用malloc/free来分配内存,但C还有一种更好的方法:new和delete。下面以动态…...
)
折半搜索(meet in the middle)
介绍 折半搜索,又称 meet in the middle \text{meet in the middle} meet in the middle,指将整个搜索过程分为两部分,并对两部分分别进行搜索,最后得到两个答案序列,将这两个答案序列进行合并,即可得到最…...
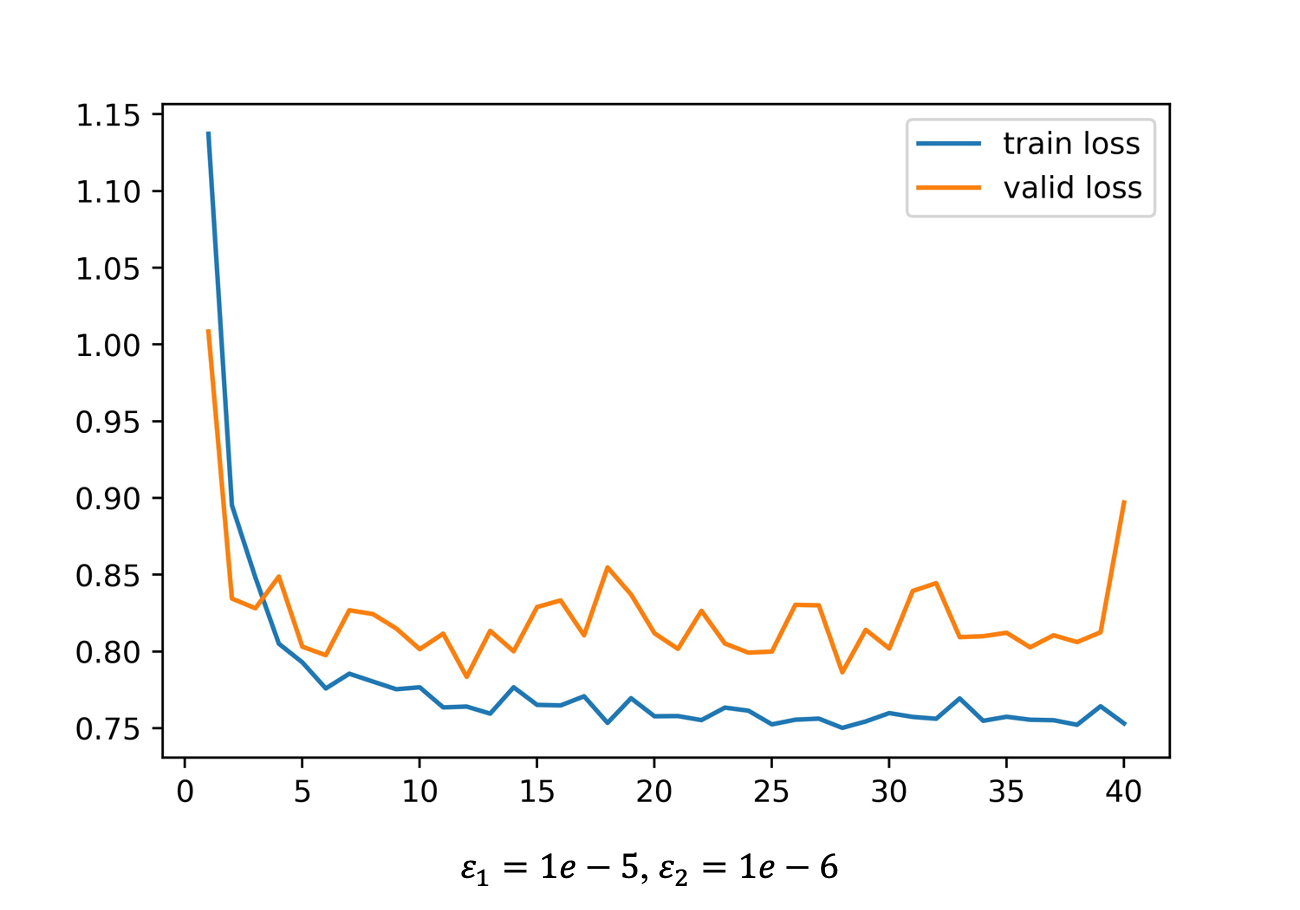
【机器学习】loss损失讨论
大纲 验证集loss上升,准确率也上升(即将overfitting?)训练集loss一定为要为0吗 Q1. 验证集loss上升,准确率也上升 随着置信度的增加,一小部分点的预测结果是错误的(log lik 给出了指数级的惩…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

涂鸦T5AI手搓语音、emoji、otto机器人从入门到实战
“🤖手搓TuyaAI语音指令 😍秒变表情包大师,让萌系Otto机器人🔥玩出智能新花样!开整!” 🤖 Otto机器人 → 直接点明主体 手搓TuyaAI语音 → 强调 自主编程/自定义 语音控制(TuyaAI…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
