Unit1_1:分治问题之时间复杂度求解
文章目录
- 背景
- 递归树法
- 案例一
- 案例二
- 局限性
- 代入法/替代法
- 主方法(重点)
背景
当碰到形如 T ( n ) = a T ( ⌈ n b ⌉ ) + O ( n d ) T(n)=aT(\lceil \frac{n}{b} \rceil)+O(n^d) T(n)=aT(⌈bn⌉)+O(nd)的递推式,本质上就是将问题转化为规模更小的子问题求解,此时有三种思路。
递归树法
案例一
T ( n ) = { 2 T ( n 2 ) + n i f n > 1 1 i f n = 1 T(n)=\left\{ \begin{array}{ll} 2T(\frac{n}{2})+n & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right. T(n)={2T(2n)+n1if n>1if n=1
可以利用递归树:
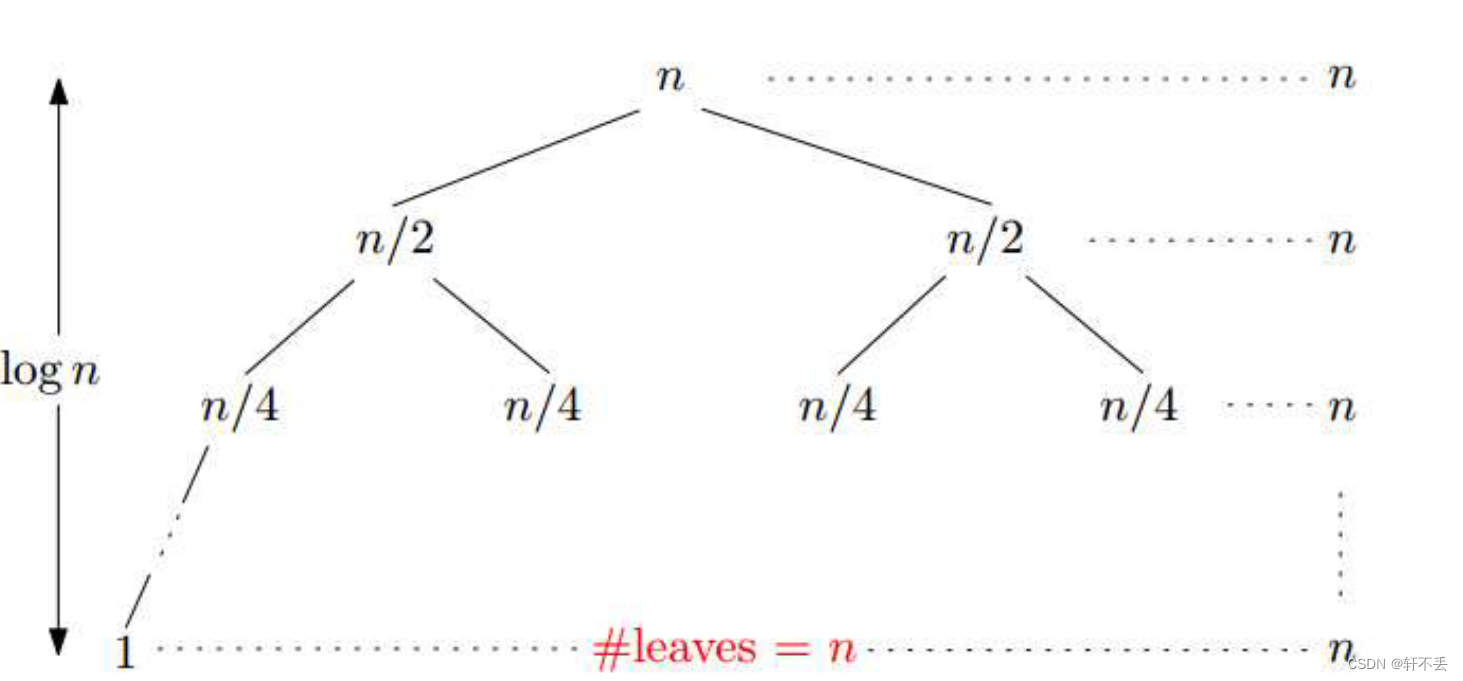
画出树,高满足 2 h = n 2^h=n 2h=n,因此 h = l o g 2 n h=log_{2}n h=log2n,而叶子共有n个,因此总的时间复杂度 T ( n ) = n l o g n T(n)=nlogn T(n)=nlogn
案例二
T ( n ) = { 3 T ( n 4 ) + n 2 i f n > 1 1 i f n = 1 T(n)=\left\{ \begin{array}{ll} 3T(\frac{n}{4})+n^2 & if \space n>1 \\ 1 & if \space n=1 \nonumber \end{array} \right. T(n)={3T(4n)+n21if n>1if n=1

每层个数即 3 h 3^h 3h个。最后一层高度 h = l o g 4 n h=log_4n h=log4n,再利用对数技巧代入,即可求出叶子的个数,而时间复杂度为:
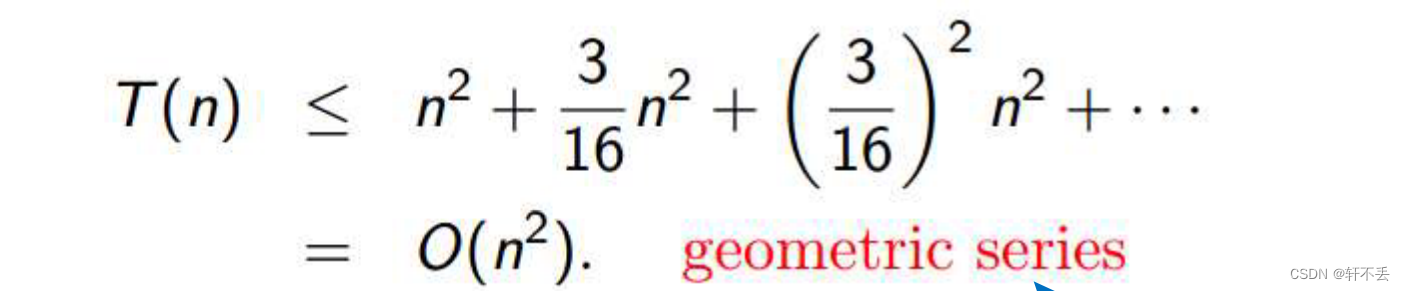
等比数列求解
局限性
T ( n ) = { T ( n 3 ) + T ( 2 n 3 ) + n i f n > 2 1 i f n = 1 , 2 T(n)=\left\{ \begin{array}{ll} T(\frac{n}{3})+ T(\frac{2n}{3})+n & if \space n>2 \\ 1 & if \space n=1,2 \nonumber \end{array} \right. T(n)={T(3n)+T(32n)+n1if n>2if n=1,2
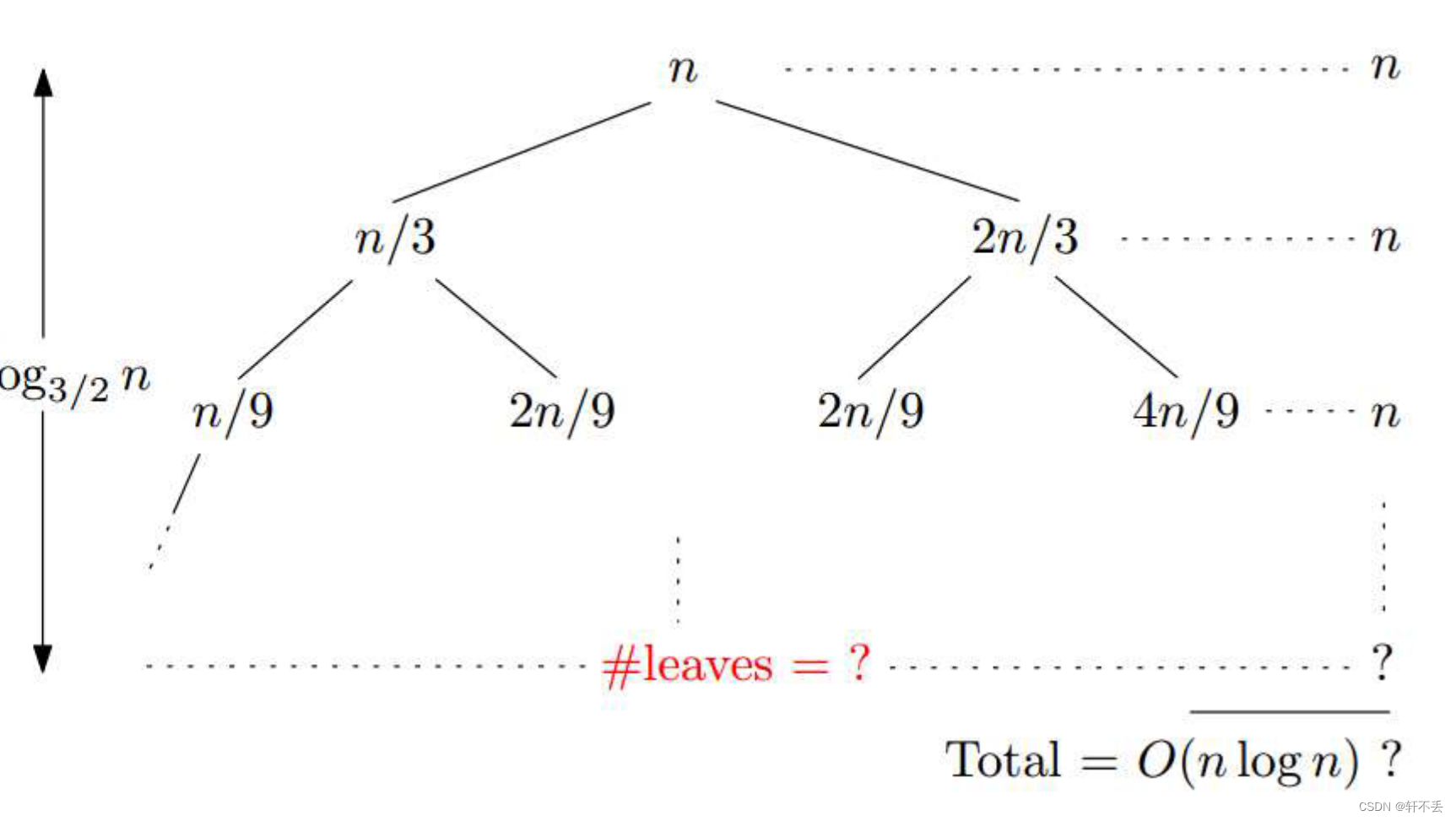
此时树的高度不一致,无法计算
代入法/替代法
此法先假设时间复杂度,再去验证假设成立。因此最难之处在于怎么假设,用处不大
主方法(重点)
T ( n ) = a T ( ⌈ n b ⌉ ) + O ( n d ) T(n)=aT(\lceil \frac{n}{b} \rceil)+O(n^d) T(n)=aT(⌈bn⌉)+O(nd)的时间复杂度如下:
T ( n ) = { O ( n d ) d > log b a O ( n d l o g n ) d = log b a O ( n log b a ) d < log b a T(n)=\left\{ \begin{array}{ll} O(n^d) & d>\log_{b}a \\\\ O(n^{d}logn) & d=\log_{b}a \\\\ O(n^{\log_{b}a}) & d<\log_{b}a \nonumber \end{array} \right. T(n)=⎩ ⎨ ⎧O(nd)O(ndlogn)O(nlogba)d>logbad=logbad<logba
以后碰到这种递推分治式子代入公式即可
相关文章:

Unit1_1:分治问题之时间复杂度求解
文章目录 背景递归树法案例一案例二局限性 代入法/替代法主方法(重点) 背景 当碰到形如 T ( n ) a T ( ⌈ n b ⌉ ) O ( n d ) T(n)aT(\lceil \frac{n}{b} \rceil)O(n^d) T(n)aT(⌈bn⌉)O(nd)的递推式,本质上就是将问题转化为规模更小的…...

React hooks的闭包陷阱
react hooks 陷阱 hooks必须放在函数顶层, 不能在条件分支和方法内 1、useState陷阱 异步陷阱 function Index() {const [count, setCount] useState(0)function add(){setCount( count 1 )console.log(count); // 0}return (<div><span>{count}…...

20.3 OpenSSL 对称AES加解密算法
AES算法是一种对称加密算法,全称为高级加密标准(Advanced Encryption Standard)。它是一种分组密码,以128比特为一个分组进行加密,其密钥长度可以是128比特、192比特或256比特,因此可以提供不同等级的安全性…...
一文详解防御DDoS攻击的几大有效办法
伴随互联网的飞速发展,网络安全问题变得越来越突出,其中最常见的就是DDoS攻击,也就是分布式拒绝服务攻击。DDoS攻击者利用计算机或其他设备的协作,以发送大量请求的方式导致目标超负荷,导致不能正常运转或“宕机”。以…...

Python二级 每周练习题24
练习一: 体重比较器 要求: 请编程实现如下功能: (1)程序开始运行时,提醒用户输入三个人的名字和体重 (可以分开输入,每次输入名字或者体重) (2) 程序自动比较,找出最重的一个人的名字和体重输出 的格式不限,但是要有最重人的姓名…...

MySQL - Buffer Pool
Buffer Pool 主要用于缓存数据库表的数据页,以提高数据库的读取性能: 缓存数据页:Buffer Pool 是 MySQL 中用于缓存数据页的内存区域。数据页通常包含数据库表的数据,如行记录等。当查询或读取数据时,MySQL会首先查看…...

c++ 拆分函数返回值和参数类型
在c中,函数参数类型和返回值类型通常是一个比较明确的信息,好像确实无需在这个上面费周折。然而,硬编码数据类型会让代码复用性下降,如果能够通过某种方式自动获取函数参数和返回值类型,对于代码的可复用性,…...

Ubuntu 23.10安装TeXlive并安装CTEX中文支持
连接上互联网,打开SHELL命令行界面, 1. sudo apt install texlive texstudio texlive-lang-chinese 就可以安装好了。texlive-lang-chinese 是TEXLIVE对CTEX中文的支持。 2. Tex源文件必须采用UTF-8编码格式,编译器采用xelatex。这样对中文…...
SpringBoot中CommandLineRunner详解(含源码)
文章目录 前言实例导入库application.yamlRunnerSpringBootCommandLineRunnerApplication执行结果 先后顺序示例OrderRunner1OrderRunner2执行结果 通常用法加载初始化数据示例 启动后打印应用信息示例 启动异步任务示例 接口健康检查示例 外部服务调用示例 参数校验示例 动态设…...
:数据传输基础)
通信基础(一):数据传输基础
一、波特率与比特率关系 比特率(信息传输速率、信息速率):指单位时间内在信道上传 送的数据量(即比特数),单位为比特每秒 (bit/s), 简记为b/s或bps。 波特率与比特率有如下换算关系: bitbaud *log 2(N) 其中, N是码元总类数。 特别注意ÿ…...

故障诊断模型 | Maltab实现BiLSTM双向长短期记忆神经网络故障诊断
文章目录 效果一览文章概述模型描述源码设计参考资料效果一览 文章概述 故障诊断模型 | Maltab实现BiLSTM双向长短期记忆神经网络故障诊断 模型描述 利用各种检查和测试方法,发现系统和设备是否存在故障的过程是故障检测;而进一步确定故障所在大致部位的过程是故障定位。故障…...

物联网和互联网医院小程序:如何实现医疗设备的远程监测和管理?
物联网(IoT)技术的发展为医疗设备的远程监测和管理提供了巨大的机会。结合互联网医院小程序,我们可以实现对医疗设备的远程访问、监控和管理,从而提高医疗服务的质量和效率。本文将介绍如何实现医疗设备的远程监测和管理ÿ…...
sharepoint2016-2019升级到sharepoint订阅版
一、升级前准备: 要建立新的sharepoint订阅版环境,需求如下: 1.单服务器硬件需求CPU 4核,内存24G以上,硬盘300G(根据要迁移的数量来扩容大小等); 2.操作系统需要windows server 20…...
CTFHub | MySQL流量、Redis流量、MongoDB流量的WriteUp
文章目录 MySQL流量题目题解 Redis流量题目题解 MongoDB流量题目题解 数据库类流量题需要用到Wireshark截取数据包,然后进行分析。 WireShark是非常流行的网络封包分析工具,可以截取各种网络数据包,并显示数据包详细信息。常用于开发测试过程…...
NSS刷题 js前端修改 os.path.join漏洞
打算刷一遍nssweb题(任重道远) 前面很简单 都是签到题 这里主要记录一下没想到的题目 [GDOUCTF 2023]hate eat snake js前端修改 这里 是对js的处理 有弹窗 说明可能存在 alert 我们去看看js 这里进行了判断 如果 getScore>-0x1e9* 我们结合上面…...
ArcGIS Maps SDK for JS:隐藏地图边框
文章目录 1 问题描述2 解决方案 1 问题描述 近期,将ArcGIS Api for JS v4.16更新到了ArcGIS Maps SDK for JS v4.27,原本去除地图的css代码失效了。 v4.26及以前版本 ,需要用.esri-view-surface--inset-outline:focus::after 控制边框属性。…...

带你秒懂MySQL!! 一万字详细知识点和基础操作 欢迎评论区怼我 (三)
表操作 创建 # 创建表结构 create table user(id int comment ID,唯一标志,username varchar(20) comment 用户名,name varchar(10) comment 姓名,age int comment 年龄,gender char(1) comment 性别 ) comment 用户表; 约束 非空约束限制该字段值不为nullnot null唯一约束保证…...

kubeadmin部署k8s1.27.4
kubeadmin部署k8s1.27.4 环境介绍 IP主机名资源配置系统版本192.168.117.170k8s-master2c2g200gCentos7.9192.168.117.171k8s-node12c2g200gCentos7.9192.168.117.172k8s-node22c2g200gCentos7.9 编辑本地解析且修改主机名 三台主机都要做 vim /etc/hosts配置主机名 mast…...

【Aurix Tricore】HighTec启动代码crt0-tc37x.c分析笔记
1. 前言 crt0是hightec 在其toolchain的gcc库中实现启动startup功能的核心代码。 HighTec已为tc3xx设置了一些默认的启动行为。在此启动过程中,目标被初始化并设置为其默认值。启动文件的代码在进入main()函数之前执行。之后,执行main()函数的构造函数。 编译器附带的启动…...

Linux高级命令(扩展)
一、find命令 1、find命令作用 在Linux操作系统中,find命令主要用于进行文件的搜索。 2、基本语法 # find 搜索路径 [选项 选项的值] ... 选项说明: -name :根据文件的名称搜索文件,支持*通配符 -type :f代表普通文…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...
