七人拼团模式:颠覆你的购物观念,499元产品让你赚翻天!
七人拼团模式是一种创新的消费模式,通过聚集消费者的购买力,让消费者能够以更优惠的价格购买到优质的商品。下面我们以499元的产品为例,详细介绍七人拼团模式的玩法规则和收益计算。

玩法规则:
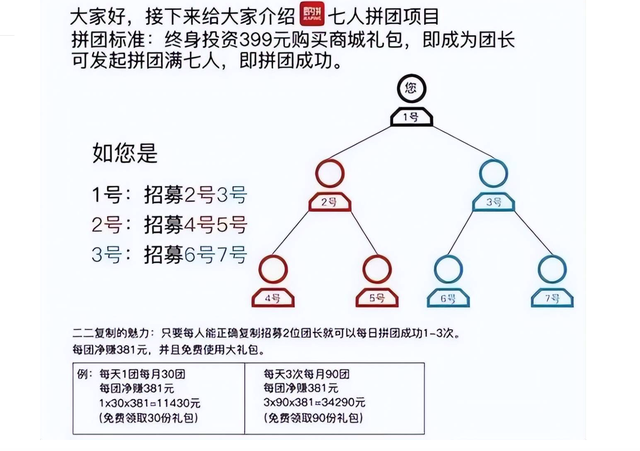
消费者购买499元的指定产品后,即可成为会员并参与拼团。
每个团需要凑齐7个会员,团长位于中心位置,其他6个会员分布在团长的周围。
拼团成功后,团长可以获得一定的收益,同时其他会员也可以以更优惠的价格购买到该产品。
收益计算:
假设每个团的团长可以获得该团销售总额的10%作为收益,同时每个会员可以获得直推下属销售额的5%作为奖励。
如果一个团销售了7个499元的产品,总销售额为3493元,那么团长可以获得的收益为:
团长收益 = 3493元 × 10% = 349.3元
此外,如果团长还直推了2个下属,每个下属也销售了7个499元的产品,那么团长还可以获得额外的奖励:
团长奖励 = 2 × (7 × 499元 × 5%) = 349.3元
因此,团长总共可以获得的收益为:
总收益 = 团长收益 + 团长奖励 = 349.3元 + 349.3元 = 698.6元
首先,七人拼团模式能够让消费者获得更优惠的价格。通过聚集消费者的购买力,商家可以提供更加优惠的价格,让消费者获得更好的购物体验。同时,团长还能够获得一定的收益,这使得消费者更加愿意参与拼团,从而形成了良性循环。
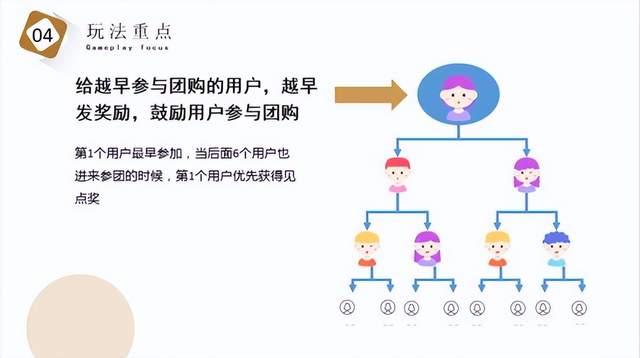
其次,七人拼团模式的机制简单易懂。消费者只需要购买指定商品并成为会员,然后分享和邀请下属参与拼团即可。排位机制也采用了二二复制公排方式,使得每个团长都能够清晰地了解自己的团队结构和人员分布情况。
最后,七人拼团模式具有较强的裂变能力。通过会员的分享和邀请,可以快速地扩大市场规模,同时也能够为商家带来更多的销售额和利润。
综上所述,七人拼团模式是一种非常有创新性和优势的消费模式,通过以499元产品为例的玩法规则和收益计算,我们可以看到它的优势和亮点。
需要咨询模式或者是软件开发的企业家,可以后台私信小编或在评论区留下您的联系方式
注明:小编所有分析的项目,只是分析商业模式
了解更多互联网资讯。需要开发 DAPP,小程序,app,分销模式,商城系统软件等关注小编
相关文章:

七人拼团模式:颠覆你的购物观念,499元产品让你赚翻天!
七人拼团模式是一种创新的消费模式,通过聚集消费者的购买力,让消费者能够以更优惠的价格购买到优质的商品。下面我们以499元的产品为例,详细介绍七人拼团模式的玩法规则和收益计算。 玩法规则: 消费者购买499元的指定产品后&…...

【机器学习合集】模型设计之卷积核设计 ->(个人学习记录笔记)
文章目录 卷积核设计1. 基于参数压缩的卷积设计1.1 【11卷积】1.2 【11卷积典型应用】1.3 【小卷积的使用】 2. 基于感受野的卷积设计2.1 膨胀卷积(带孔卷积,strous convolution)2.2 可变形卷积2.3 非局部卷积 3. 基于卷积操作的优化3.1 移位网络3.2 加法网络 卷积核…...

JS实现用户二次确认后再提交表单
HTML代码 <form id"importForm" action"" method"post" enctype"multipart/form-data" onsubmit"return confirmSubmit()"> ...... <input id"btnImportSubmit" class"btn btn-primary" type…...
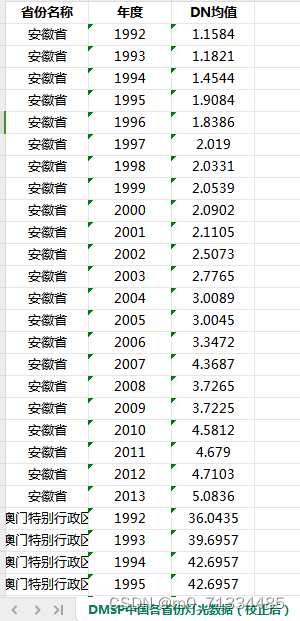
1992-2021年全国各省经过矫正的夜间灯光数据(GNLD、VIIRS)
1992-2021年省市县经过矫正的夜间灯光数据(GNLD、VIIRS) 1、时间:1992-2021年3月,其中1992-2013年为年度数据,2013-2021年3月为月度数据 2、来源:DMSP、VIIRS 3、范围:31省 4、指标解释&…...
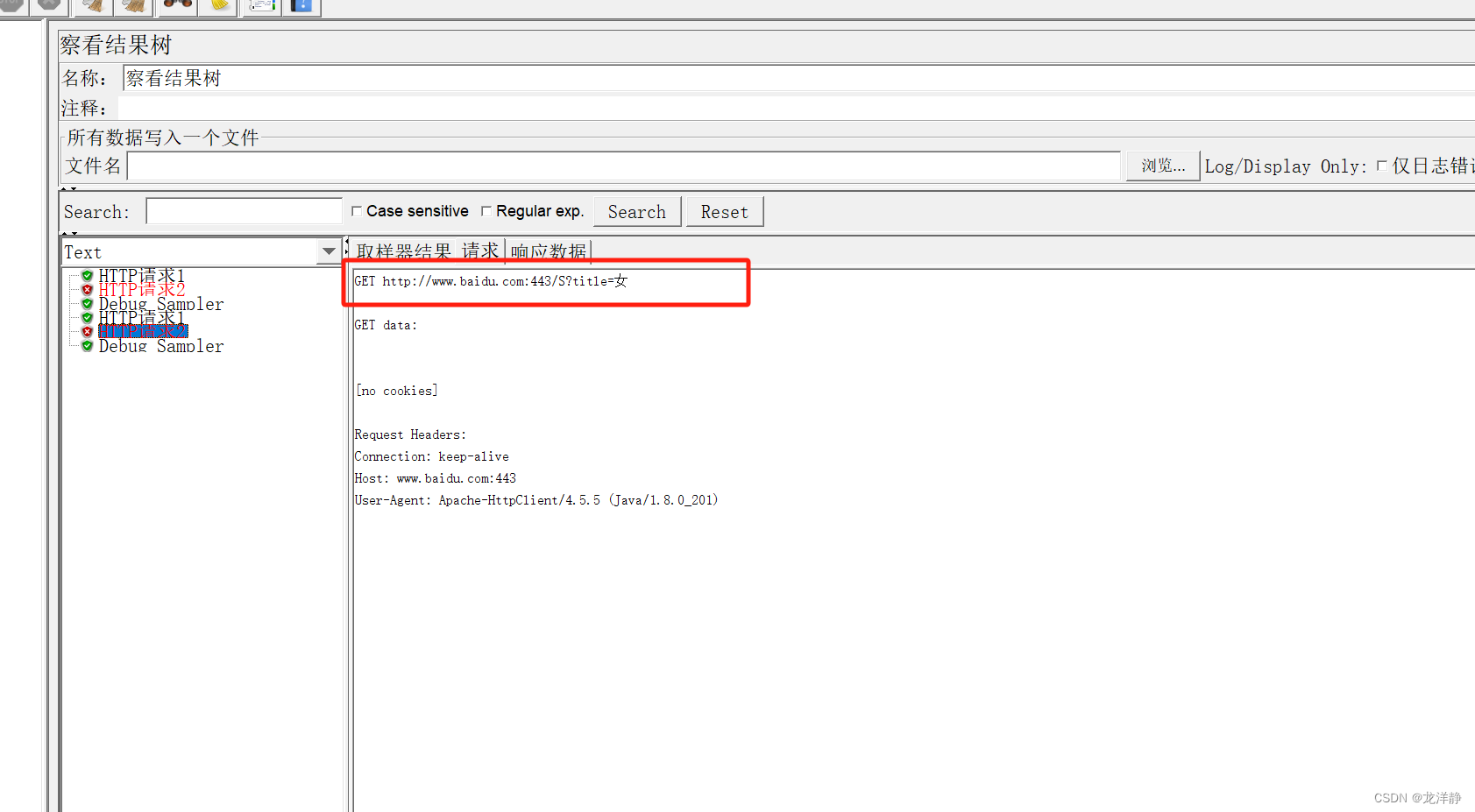
JMeter的使用——傻瓜式学习【中】
目录 前言 1、JMeter参数化 1.1、什么是参数化 1.2、用户定义的变量 1.2.1、什么时候使用用户定义的变量 1.2.2、使用“用户定义的变量”进行参数化的步骤: 1.2.3、案例 1.3、用户参数 1.3.1、什么时候使用用户参数? 1.3.2、使用“用户参数”进…...

MyBaties存储和查询json格式的数据(实体存储查询版本)
最近在做的功能,由于别的数据库有值,需要这边的不同入口的进来查询,所以需要同步过来,如果再继续一个一个生成列对应处理感觉不方便,如果没有别的操作,只是存储和查询,那就可以用MySql支持的jso…...

动态规划14:一和零
动态规划14:一和零 题目 474. 一和零 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。 …...
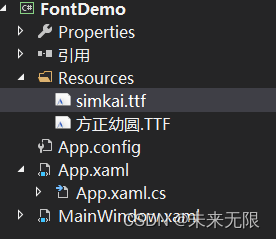
C#WPF嵌入字体实例
本文介绍C#WPF嵌入字体实例。 首先创建项目 添加Resources文件夹,添加字体文件,字体文件属性:生成操作为Resources,复制到输出目录:不复制 字体的使用可以采用以下两种方法: 方式一 直接引用 FontFamily="./Resources/#幼圆" 方式二 定义资源 <Applica…...

Linux——Linux权限
Linux权限 前言一、shell命令以及运行原理二、Linux权限的概念Linux权限管理文件访问者的分类(人)文件类型和访问权限(事物属性)文件权限值的表示方法文件访问权限的相关设置方法 file指令目录的权限粘滞位 总结 前言 linux的学习…...

android中gradle的kotlin编译配置选项
一、编译配置 1、Android中的配置 使用如下方式开启在Android中的gradle的kotlin编译配置: 该配置在其余平台不可用 android {...compileOptions {sourceCompatibility JavaVersion.VERSION_17targetCompatibility JavaVersion.VERSION_17}kotlinOptions {jvmTar…...
【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别))
【知识串联】概率论中的值和量(随机变量/数字特征/参数估计)【考研向】【按概率论学习章节总结】(最大似然估计量和最大似然估计值的区别)
就我的概率论学习经验来看,这两个概念极易混淆,并且极为重点,然而,在概率论的前几章学习中,如果只是计算,对这方面的辨析不清并没有问题。然而,到了后面的参数估计部分,却可能出现问…...

NOIP2023模拟6联测27 点餐
题目大意 有 n n n样菜品,每样菜品都有两个权值 a i a_i ai和 b i b_i bi,如果你选择了 k k k个菜品,分别为 p 1 , … , p k p_1,\dots,p_k p1,…,pk,则你的花费为 ∑ i 1 k a p i max i 1 k b p i \sum\limits_{i…...
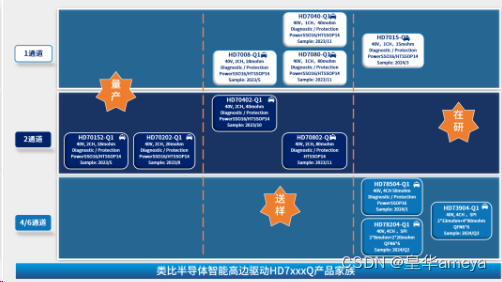
AMEYA360:类比半导体重磅发布车规级智能高边驱动HD7xxxQ系列
致力于提供高品质芯片的国内优秀模拟及数模混合芯片设计商上海类比半导体技术有限公司(下称“类比半导体”或“类比”)宣布推出重磅新品车规级智能高边驱动HD7xxxQ系列。该系列产品包括车规级单通道高边驱动HD70xxQ和车规级双通道智能高边驱动HD70xx2Q,提供不同通道…...

【HarmonyOS】鸿蒙操作系统架构
HarmonyOS架构 一. 鸿蒙系统定位二. 架构整体遵从分层设计三. HarmonyOS具有的技术特性四. HarmonyOS有三大特征 其它相关推荐: 软考系统架构之案例篇(架构设计相关概念) 系统架构之微服务架构 系统架构设计之微内核架构 所属专栏:系统架构设计师 一. 鸿…...
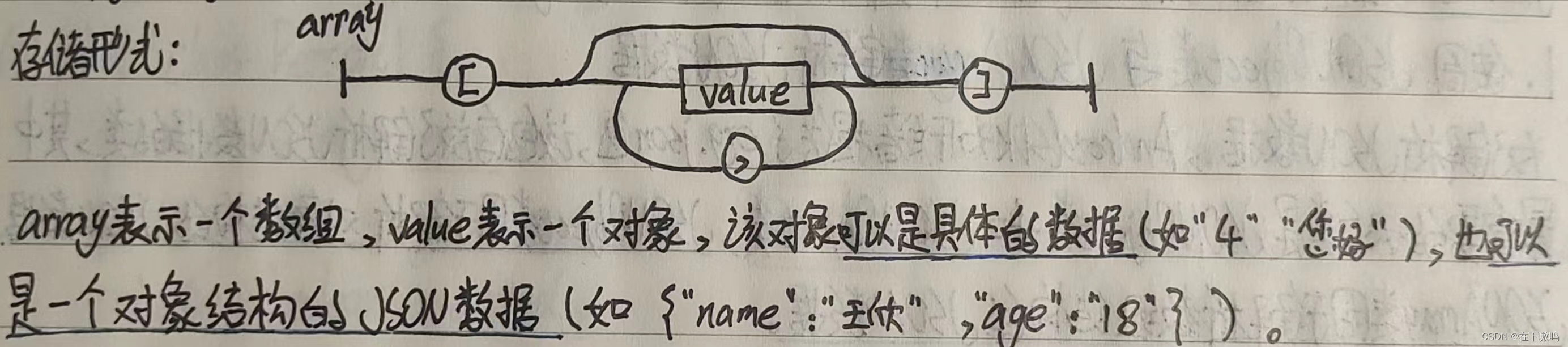
JSON数据
一、JSON介绍 Android应用程序界面上的数据信息大部分都是通过网络请求从服务器上获取到的,获取到的数据类型常见的就是JSON。JSON是一种新的数据格式,这种格式的数据不可以直接显示到程序的界面上,需要将该数据解析为一个集合或对象的形式才…...

金融领域:怎么保持电力系统连续供应?
银行作为金融领域的关键机构,依赖于高度可靠的电力供应,以保持银行操作的连续性。在电力中断或电力质量问题的情况下,银行可能面临严重的风险,包括数据丢失、交易中断和客户满意度下降。 UPS监控系统在这一背景下变得至关重要&…...
批量重命名文件夹:用数字随机重命名法管理您的文件夹
在文件管理中,文件夹的命名是一项至关重要的任务。一个好的文件夹命名方案可以帮助我们更高效地组织和查找文件。然而,随着时间的推移,我们可能会遇到文件夹数量过多,难以管理和查找的问题。为了解决这个问题,我们可以…...

RPC与HTTP的关系
首选理清楚关系 RPC与HTTP是两个不同维度的东西 HTTP 协议(Hyper Text Transfer Protocol),又叫做超文本传输协议,是一种传输协议,平时通过浏览器浏览网页网页,用到的就是 HTTP 协议。 而 RPC࿰…...

OpenCV #以图搜图:感知哈希算法(Perceptual hash algorithm)的原理与实验
1. 介绍 感知哈希算法(Perceptual Hash Algorithm,简称pHash) 是哈希算法的一种,主要用来做相似图片的搜索工作。 2. 原理 感知哈希算法(pHash)首先将原图像缩小成一个固定大小的像素图像,然后…...
Android多张图片rotation旋转角度叠加/重叠堆放
Android多张图片rotation旋转角度叠加/重叠堆放 <?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:app"http://schemas.android.com/apk/res-auto"…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
